Metode Numerik Darell Jeremia Sitompul 21067272922

Case study of hydrogen storage Optimization project, Darell Jeremia Sitompul

When optimizing hydrogen storage, several factors must be considered to ensure efficiency, safety and practicality. Here are some important considerations:

1. Storage method: There are various methods of storing hydrogen, including compressed gas, liquid, metal hydride, and chemical storage. Each method has advantages and limitations, so your specific use and needs will determine which storage method is best for you.

2. Storage density: The key is to maximize the amount of hydrogen that can be stored within a given volume or mass. Higher storage densities reduce space and weight requirements, making them more practical for a variety of applications. The goal is to improve charging efficiency, increase the energy density of hydrogen, or discover new storage materials.

3. Security: Hydrogen is highly flammable and requires special precautions to ensure safe storage and handling. Minimizing the risk of leaks, preventing explosions and developing robust safety systems are essential. Consideration should be given to material compatibility, structural integrity and adequate ventilation mechanisms.

4. Storage efficiency: Hydrogen storage efficiency indicates how much of the energy used can be recovered when hydrogen is used. It is important to minimize energy loss during storage due to heat transfer, leakage, etc. With high storage efficiency, stored hydrogen can be used effectively when needed.

5. Durability and long life: Hydrogen storage systems must be designed for long-term use without significant degradation. Considerations include material stability, corrosion resistance, fatigue, and other degradation mechanisms. Longevity is very important to reduce maintenance and ensure the economics of hydrogen storage systems.

6. Cost: The cost of hydrogen storage is an important factor that determines its economics. Cost-effective optimization of storage methods includes factors such as material costs, manufacturing processes, system integration and scalability. Cost-cutting measures could accelerate the adoption of hydrogen storage technology.

7. Temperature and pressure: The storage method should consider the optimal temperature and pressure conditions for hydrogen storage. Different storage materials and technologies may have specific requirements for maintaining hydrogen in the desired state (gas, liquid, adsorption, etc.).

8. Environmental Impact: Environmental impacts associated with hydrogen storage methods must be considered. For example, the production and disposal of stored materials, energy consumption during storage, and potential greenhouse gas emissions during the hydrogen lifecycle.

9. Infrastructure Compatibility: In order to be widely accepted, hydrogen storage systems must be compatible with existing or planned hydrogen infrastructure such as production, distribution and utilization facilities. Integration into established infrastructure reduces implementation challenges.

10. Compliance with Regulations and Standards: Compliance with applicable safety, quality and performance standards and regulations is critical to the safe and reliable operation of hydrogen storage systems. Compliance with standards facilitates market acceptance and regulatory approval.

11. Security Measures: The implementation of safety features such as pressure relief valves, leak detection systems and fail-safe mechanisms is essential to minimize the risk of accidents and hazards associated with hydrogen storage.

Hydrogen storage optimization is the process of improving the storage and handling of hydrogen gas, a promising clean energy carrier. Hydrogen has great potential as a renewable and sustainable energy source, but one of the challenges associated with its use is efficient storage and supply.

Various methods are used to optimize hydrogen storage, including:

1. Compressed gas storage: Hydrogen can be stored in high pressure tanks. By compressing hydrogen gas to high pressures (typically 350-700 bar), it can be stored in relatively small volumes. However, this method requires a sturdy and heavy storage tank and requires energy to compress the gas. Due to the high pressure, safety is also important.

2. Liquid hydrogen storage: Hydrogen can be cooled and stored as a cryogenic liquid at cryogenic temperatures (-253 °C). Storing liquid hydrogen allows for high energy densities, but requires specialized cryogenic containers and large amounts of energy for liquefaction. In addition, there are challenges with hydrogen flash-off and insulation of storage vessels.

3. Solid state hydrogen storage: Various materials such as metal hydrides, complex hydrides, and carbon-based materials can store hydrogen within their structures. These materials can release hydrogen when heated or exposed to certain conditions. Research is focused on finding materials with high hydrogen storage capacity, favorable kinetics for hydrogen release and absorption, and reasonable operating conditions.

4. Underground storage: Hydrogen can be stored in underground formations such as depleted oil and gas reservoirs and salt caves. This method uses existing infrastructure and large storage capacities. Hydrogen is injected into the formation and stored under pressure. However, the suitability of a particular geological formation for hydrogen storage must be evaluated and safety aspects must be considered.

Optimizing hydrogen storage involves improving the efficiency, safety and practicality of these storage methods. This includes developing advanced materials with higher storage capacities, improving tank design, optimizing system integration, improving hydrogen supply and fueling infrastructure, and reducing the energy required for compression or liquefaction. .

Research and development is currently underway to improve hydrogen storage technology and make it more economical, scalable and accessible for various applications such as transportation, energy storage and industrial processes.

Final Report of Hydrogen Storage Optimization Project, Darell Jeremia Sitompul

Requirement:

- Capacity = 1 Liter

- Budget = Rp.500.000,00 (Lima ratus ribu rupiah)

---

---

First of all, to start doing the calculation, I would like to imagine the ideal shape for a hydrogen storage. My assumption would be a form of a capsule.

Here is the visualization model (Made with Autodesk Inventor Professional 2022).

And the cross section 2 dimensional view from the centerline will look like this.

---

We need to optimize the storage surface area to a minimum and keep the volume at 1 liter. The storage space volume is fixed at 1 liter, but there are many combinations of radius and flat tube height. We can use programming to help us save alot of calculation time.

Finding Smallest Surface Area of the capsule with radius from 0 to 20 centimeters

Here is the code:

   import numpy as np
   
   
   print(":    Radius    :    Surface Area    :")
     
   r_max = 20
   a = np.zeros((r_max, 2))
   
   for r in range (1, r_max + 1):
       flat_tube_height = (1000-((4*np.pi*r**3)/3))/(np.pi*(r)**2)
       sur_area = ((2*np.pi*r) * flat_tube_height) + ((2*np.pi*r**2)*2)
       a[r-1][0] = int(r)
       a[r-1][1] = np.round(sur_area, 5)
       print(":    ", a[r-1][0], " "*(6 - len(str(a[r-1][0]))),
         " :    ", a[r-1][1], " "*(12 - len(str(a[r-1][1]))), " :")
   b = a
   
   for i in range(len(b)):
       for j in range (len(b)):
           if b[i][1] < b[j][1]:
                   for n in range (2):
                           temp = b[i][n]
                           b[i][n] = b[j][n]
                           b[j][n] = temp
                           
   print("Minimum surface area will be found when")
   print("Radius = ", b[0][0])
   print("Surface Area : ", b[0][1])

When we run the program, the result will be shown like this

   :    Radius    :    Surface Area    :
   :     1.0      :     2004.18879     :
   :     2.0      :     1016.75516     :
   :     3.0      :     704.36578      :
   :     4.0      :     567.02064      :
   :     5.0      :     504.71976      :
   :     6.0      :     484.12978      :
   :     7.0      :     490.96501      :
   :     8.0      :     518.08257      :
   :     9.0      :     561.51423      :
   :     10.0     :     618.87902      :
   :     11.0     :     688.6618       :
   :     12.0     :     769.85246      :
   :     13.0     :     861.7517       :
   :     14.0     :     963.86002      :
   :     15.0     :     1075.81113     :
   :     16.0     :     1197.33029     :
   :     17.0     :     1328.20743     :
   :     18.0     :     1468.27914     :
   :     19.0     :     1617.41642     :
   :     20.0     :     1775.51608     :
   Minimum surface area will be found when
   Radius =  6.0
   Surface Area :  484.12978

We see that there is a decrease and increase in the value of the capsule area from radius 5 cm to 6 cm and from radius 6 cm to 7 cm respectively. We can find more precise result of the minimum surface area by reducing the radius range only from 5 cm to 7 cm.

We can use smaller difference of radius within iterations than the first program from 1 cm difference by each iterations to 10^(-5) cm difference.

Here is the code:

   import numpy as np
   
   a = []
   
   r = 5
   
   while True:
     flat_tube_height = (1000-((4*np.pi*r**3)/3))/(np.pi*(r)**2)
     sur_area = ((2*np.pi*r) * flat_tube_height) + ((2*np.pi*r**2)*2)
     a.append((sur_area, r))
     r += 1e-5
     if r > 7:
       break
   print(min(a))

When we run the program, the result is being shown like below:

   (483.5975862052437, 6.203499999954438)

The numerically minimum surface area can be obtained when the radius is about 6.20349 cm and the value of numerically minimum surface area is about 483.59758 cm^2.

---

Now we need to find the thickness of our material so that the storage could withstand the pressure of the hydrogen inside.

The material chosen is Aluminum 6061-T6 that has yield strength equal to 276 MPa.

Let's calculate theoretical hoop stress of the required hydrogen gas pressure using Python program.

   import numpy as np
   
   
   print(": Thickness (mm) :  Hoop Stress (MPa)  :")
   r = 6.20349e-2
   p = 0.8
   t = 1
   mylist = [] 
   while t < 14:
     hoop_stress = (r * p * 1000)/(t)
     mylist.append((t, hoop_stress))
     print(":      ", mylist[t-1][0], " "*(6 - len(str(mylist[t-1][0]))),
           " :      ", np.round(mylist[t-1][1],5), " "*(11 - len(str(np.round(mylist[t-1][1],5)))), " :")
     t += 1

And we get the following result

   : Thickness (mm) :  Hoop Stress (MPa)  :
   :       1        :       49.62792      :
   :       2        :       24.81396      :
   :       3        :       16.54264      :
   :       4        :       12.40698      :
   :       5        :       9.92558       :
   :       6        :       8.27132       :
   :       7        :       7.0897        :
   :       8        :       6.20349       :
   :       9        :       5.51421       :
   :       10       :       4.96279       :
   :       11       :       4.51163       :
   :       12       :       4.13566       :
   :       13       :       3.81753       :

We see that the thinnest option of the coding (in this case, 1 mm) has hoop stress almost 50 MPa (barely more than a fifth of our material Yield Strength).

If we modify the formula of Hoop stress to get the thickness so that the hoop stress approaches 276 MPa, we get the thickness is about 0.0001798113 mm. But in industrial level, there is no such Aluminum 6061 with that thickness being mass produced.

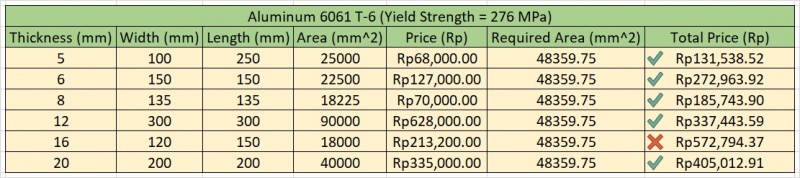
That means we should see the available option from which thickness are available on the market.

Note that there are many available options in the market, but not every options are suitable to our requirements. The example is the 16 mm thickness option if we calculated it into out required surface area, the cost exceeds Rp500.000,00 (The maximum budget).

Therefore, we have 5 option that costs below Rp500.000,00. But we need to eliminate some options based on price. Since option 5 mm and 8 mm thickness are relatively cheaper than the other, we can choose either 5 mm thickness or 8 mm thickness.

Even if 5 mm and 8 mm thickness are cost-effective, we choose the option that can withstand greater stress and have bigger safety factor. Therefore, we prefer 8 mm thickness option for our Hydrogen Storage Tank.