Difference between revisions of "Cost Analysis"
(Created page with "Berikut adalah contoh kode Python untuk melakukan analisis biaya pada desain tabung hidrogen yang optimal: def volume_cylinder(height, radius): return np.pi * radius**2 *...") |
|||
| Line 1: | Line 1: | ||
| − | + | from scipy.optimize import minimize | |
| + | # Harga dan kapasitas | ||
| + | harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen = 1 | ||
| + | # Kapasitas penyimpanan hidrogen per unit | ||
| + | # Anggaran maksimal | ||
| + | budget_maksimal = 500000 | ||
| + | # Fungsi tujuan | ||
| + | def fungsi_tujuan(x): | ||
| + | return -x | ||
| + | # Kendala | ||
| + | def kendala(anggaran): | ||
| + | return budget_maksimal - (harga_per_unit * anggaran) | ||
| + | kendala_anggaran = {'type': 'ineq', 'fun': kendala} | ||
| + | # Nilai awal | ||
| + | x0 = 0 | ||
| + | # Batasan | ||
| + | batas = [(0, None)] | ||
| + | # Menyelesaikan masalah optimisasi | ||
| + | solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran]) | ||
| + | # Menampilkan hasil | ||
| + | print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi") | ||
| + | print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0]) | ||
| + | print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter") | ||
| + | print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | ||
| − | + | [[File:500px-Hasil_optimasi.png]] | |
| − | |||
| − | + | Untuk menunjukan grafik mengenai optimisasi penyimpanan hidrogen antara kapasitas dan anggaran dapat digunakan phyton code di bawah ini : | |
| − | |||
| − | + | <syntaxhighlight lang="xml"> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | import numpy as np | |
| − | + | import matplotlib.pyplot as plt | |
| − | + | from scipy.optimize import minimize | |
| − | # | + | # Harga dan kapasitas |
| − | + | harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen | |
| + | kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit | ||
| − | # | + | # Anggaran maksimal |
| − | + | budget_maksimal = 500000 | |
| − | |||
| − | |||
| − | |||
| − | + | # Fungsi tujuan | |
| + | def fungsi_tujuan(x): | ||
| + | return -x | ||
| − | + | # Kendala | |
| + | def kendala(x): | ||
| + | return budget_maksimal - (harga_per_unit * x[0]) | ||
| − | + | kendala_anggaran = [{'type': 'ineq', 'fun': kendala}] | |
| + | |||
| + | # Nilai awal | ||
| + | x0 = [0] | ||
| + | |||
| + | # Batasan | ||
| + | batas = [(0, None)] | ||
| + | |||
| + | # Membuat fungsi untuk menampilkan hasil | ||
| + | def tampilkan_hasil(solusi): | ||
| + | print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi") | ||
| + | print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0]) | ||
| + | print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter") | ||
| + | print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | ||
| + | |||
| + | # Menyelesaikan masalah optimisasi | ||
| + | solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran) | ||
| + | |||
| + | # Menampilkan hasil | ||
| + | tampilkan_hasil(solusi) | ||
| + | |||
| + | # Menghasilkan grafik | ||
| + | anggaran = np.linspace(0, 10, 100) # Range anggaran | ||
| + | kapasitas = anggaran * kapasitas_per_unit # Total kapasitas penyimpanan untuk setiap anggaran | ||
| + | biaya = anggaran * harga_per_unit # Total biaya untuk setiap anggaran | ||
| + | |||
| + | plt.figure() | ||
| + | plt.plot(anggaran, kapasitas, label='Kapasitas Penyimpanan') | ||
| + | plt.plot(anggaran, biaya, label='Total Biaya') | ||
| + | plt.axhline(solusi.x[0] * kapasitas_per_unit, color='r', linestyle='--', label='Jumlah Unit Optimal') | ||
| + | plt.axvline(solusi.x[0], color='g', linestyle='--', label='Anggaran Optimal') | ||
| + | plt.xlabel('Anggaran') | ||
| + | plt.ylabel('Kapasitas/Biaya') | ||
| + | plt.title('Optimisasi Penyimpanan Hidrogen') | ||
| + | plt.legend() | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | [[File:500px-graph.png]] | ||
| + | |||
| + | |||
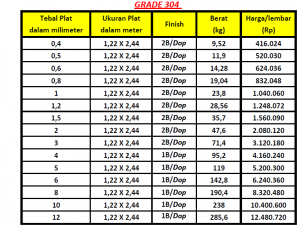
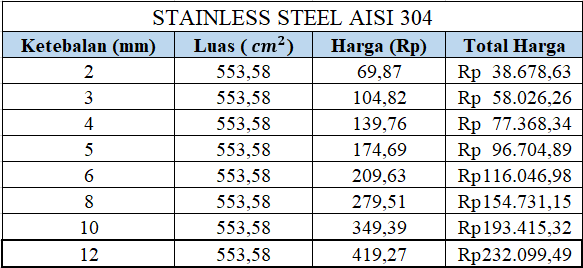
| + | Material yang dipakai untuk tabung penyimpanan hidrogen ini adalah AISI 304. Material ini memiliki kekuatan yang baik dan memiliki ketahanan suhu yang sesuai dengan sifat hidrogen. Material ini juga secara harga sangat terjangkau. Berikut 'Mechanical Properties AISI 304' : | ||
| + | |||
| + | [[File:AISI304.png]] | ||
| + | |||
| + | [[File:HargaPerusahaanAISI304.png|300x300px]] | ||
| + | [[File:HargaAISI304.png]] | ||
| + | |||
| + | Dari harga di atas, kita dapat mengambil stainless steel AISI 304 dengan ketebalan 12 mm. | ||
Latest revision as of 02:32, 12 June 2023
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen = 1
# Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(anggaran):
return budget_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
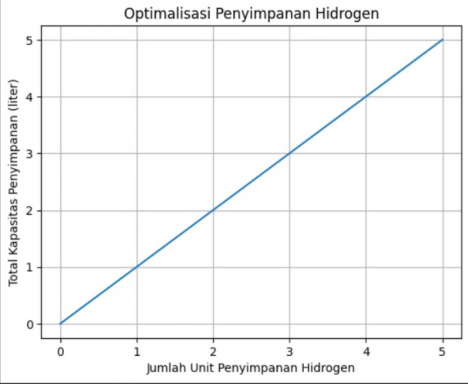
Untuk menunjukan grafik mengenai optimisasi penyimpanan hidrogen antara kapasitas dan anggaran dapat digunakan phyton code di bawah ini :
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen
kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(x):
return budget_maksimal - (harga_per_unit * x[0])
kendala_anggaran = [{'type': 'ineq', 'fun': kendala}]
# Nilai awal
x0 = [0]
# Batasan
batas = [(0, None)]
# Membuat fungsi untuk menampilkan hasil
def tampilkan_hasil(solusi):
print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran)
# Menampilkan hasil
tampilkan_hasil(solusi)
# Menghasilkan grafik
anggaran = np.linspace(0, 10, 100) # Range anggaran
kapasitas = anggaran * kapasitas_per_unit # Total kapasitas penyimpanan untuk setiap anggaran
biaya = anggaran * harga_per_unit # Total biaya untuk setiap anggaran
plt.figure()
plt.plot(anggaran, kapasitas, label='Kapasitas Penyimpanan')
plt.plot(anggaran, biaya, label='Total Biaya')
plt.axhline(solusi.x[0] * kapasitas_per_unit, color='r', linestyle='--', label='Jumlah Unit Optimal')
plt.axvline(solusi.x[0], color='g', linestyle='--', label='Anggaran Optimal')
plt.xlabel('Anggaran')
plt.ylabel('Kapasitas/Biaya')
plt.title('Optimisasi Penyimpanan Hidrogen')
plt.legend()
plt.grid(True)
plt.show()
Material yang dipakai untuk tabung penyimpanan hidrogen ini adalah AISI 304. Material ini memiliki kekuatan yang baik dan memiliki ketahanan suhu yang sesuai dengan sifat hidrogen. Material ini juga secara harga sangat terjangkau. Berikut 'Mechanical Properties AISI 304' :
Dari harga di atas, kita dapat mengambil stainless steel AISI 304 dengan ketebalan 12 mm.