Mei Edi Prayitno

Mei Edi Prayitno No.18.062.444.65

Definisi

Komputasi adalah algoritma yang digunakan untuk menemukan suatu cara dalam memecahkan masalah dari sebuah data input. Data input disini adalah sebuah masukan yang berasal dari luar lingkungan sistem. Komputasi ini merupakan bagian dari ilmu komputer berpadu dengan ilmu matematika. Secara umum ilmu komputasi adalah bidang ilmu yang mempunyai perhatian pada penyusunan model matematika dan teknik penyelesaian numerik serta penggunaan komputer untuk menganalisis dan memecahkan masalah-masalah ilmu (sains). Dalam penggunaan secara umum, biasanya berupa penerapan simulasi komputer atau berbagai bidang keilmuan, tetapi dalam perkembangannya digunakan juga untuk menemukan prinsip-prinsip baru yang mendasar terhadap bidang ilmu yang mendasari teori ini. Bidang ini berbeda dengan ilmu komputer (computer science), yang mengkaji komputasi, komputer dan pemrosesan informasi. Bidang ini juga berbeda dengan teori dan percobaan sebagai bentuk tradisional dari ilmu dan kerja keilmuan. Dalam ilmu alam, pendekatan ilmu komputasi dapat memberikan berbagai pemahaman baru, melalui penerapan model-model matematika dalam program komputer berdasarkan landasan teori yang telah berkembang, untuk menyelesaikan masalah-masalah nyata dalam ilmu tersebut. Komputasi modern bisa disebut sebuah konsep sistem yang menerima intruksi-intruksi dan menyimpannya dalam sebuah memory, memory disini bisa juga dari memory komputer. Oleh karena pada saat ini kita melakukan komputasi menggunakan komputer maka bisa dibilang komputer merupakan sebuah komputasi modern. Konsep ini pertama kali digagasi oleh John Von Neumann (1903-1957). Dalam kerjanya komputasi modern menghitung dan mencari solusi dari masalah yang ada, dan perhitungan yang dilakukan itu meliputi:Akurasi, Kecepatan, ProblemVolume Besar, Modelling dan Kompleksitas

Pemodelan (Modelling)

Pemodelan dilakukan dengan memahami pada konsep berikir, untuk mencari hal yang baru dan bermanfaat bagi kehidupan manusia. Dalam konsep pemodelan (Modelling) tidak berhenti pada konsep definisi saja, akan tetapi akan terus digali pada semua jenis kebutuhan sesuai kebutuhan manusia. oleh karenanya memberikan peluang untuk terus menggali pada kemanfaatan bagi manusia. Pembelajaran tersebut dilakukan pada berbagai bidang seperti mecahnical yang secara spesifik pada berbagai disiplin ilmu seperti: electrical, kimia, geologi, design manufacture, dll. Untuk meningkatkan kemampuan dalam menelaahan tersebut diperlukan daya (Force) yang menjadi latar belakang dalam penyiapan modelling untuk menyerderhanakan permasalahan yang akan diselesaikan yang bersifat rumit. Pemodelan (Modelling) tersebut dilakukan dengan model fisik, maupun dengan model komputasi yang dilakukan dengan model model matematika. seperti halnya pada pemodelan sebuah jembatan, maka pemodelan dilakukan dengan model sesuai skala (simplifikasi) dengan tujuan untuk memudahkan dalam penyelesaian beban-beban yang akan bekerja. Dengan demikian diharapkan akan mampu merefleksikan dari kondisi yang sebenarnya. Pada pemodelan tersebut diperlukan model matematika yang diselesaikan secara numerik. Model tersebut didasarkan pada persepsi, yang didasarkan pada sense. Dalam persepsi tersebut perlu menggunakan rasio, dalam batas-batas yang telah ditentukan. Rasio tersebut didasarkan pada kaidah-kaidah yang telah ditentukan seperti kaidah agama, moral dan etika. Begitupun juga dalam dalam penyelesaian berbagai permasalahan teknik, seperti mechanical, segala penyelesaian yang dilakukan tidak melampaui dari aturan baku yang telah ditetapkan. Seeperti halnya pda kehidupan nyata, apabila insan senantiasa dapat mengingat Allah (Tuhan YME) akan senantiasa menepati jalan yang telah ditentukan, sehingga akan dapat mencapai keselamatan.

Tahapan Pemodelan (modelling)

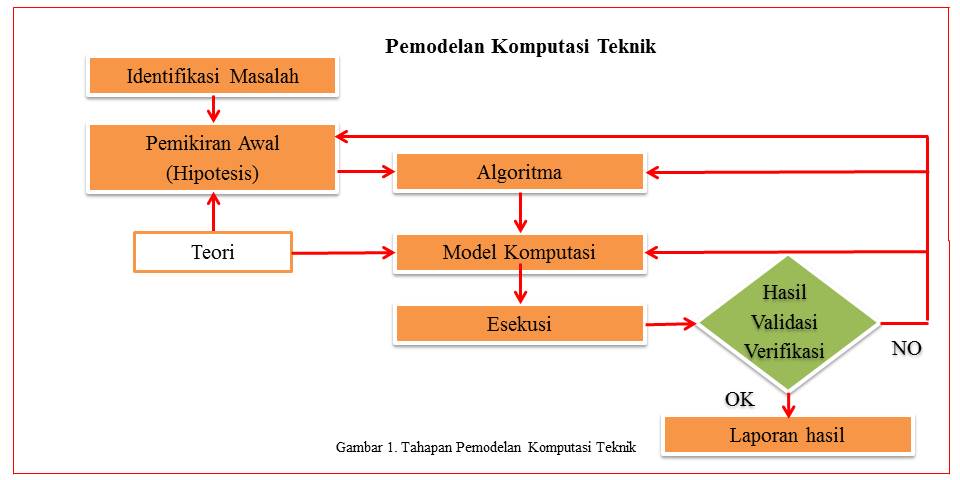
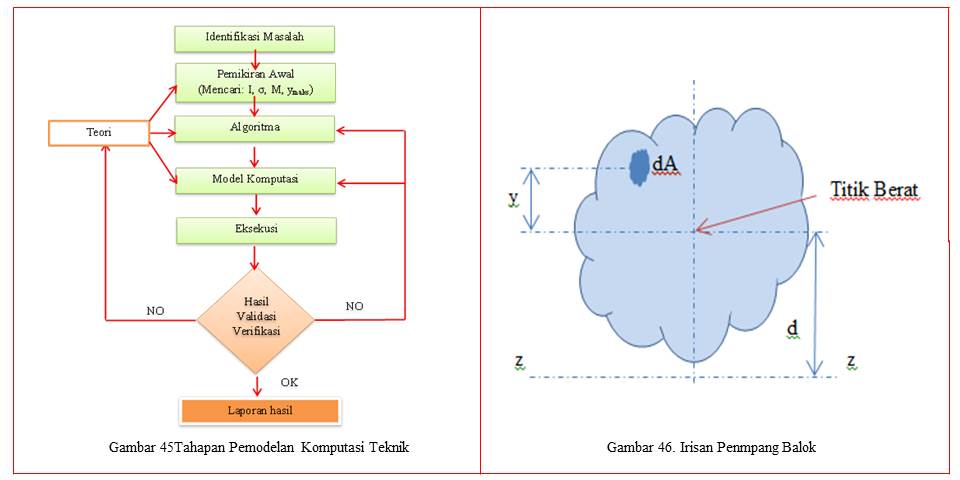
Pada kegiatan pemodelan komputasi teknik seperti yang ditunjukkan pada gambar 1, meliputi beberapa tahapan sebagai berikut:

1. Masalaah (Problem). Yaitu apa saja yang menjadi permasalahan, sehingga dapat ditentukan bagaimana metode penyelesaian dan bagaimana model matematikanya. Misal dalam pembuatan rumah permasalahn yang ada adalah bagaimana bentuk (geometri) dari rumah tersebut dan material apa yang akan dilakukan. untuk itu diperlukan sebuah penelahaan yang dilakukan secara terintegrasi dari beberapa aspek, seperti kekuatan, keselamatan, ketahanan terhadap beban. Untuk dapat mewujudkan hal yang dikehendaki diperlukan asumsi yang dibuat berdasarkan pada kemampuan Brainware (Manusia/analist) maupun pada Software dn Hardware. Permasalahan tersebut dapat berupa permasalahan yang ada saat ini (existing) maupun permasalahan yang diprediksi akan timbul disuatu saat apabila upaya solusinya tidak dilakukan.

2. Pemikiran Awal (Analisis Awal). Analisis awal adalah asumsi yang dilakukan dalam upaya untuk mencari jawaban sementara (Hiphotesis). Semua hasil penelitian adalah Hipotesis kecuali Kitab Suci (Alquran) yang merupakan sebuah Tesis sejati (The Thrully Theses). Seperti halnya dalam falsafah hidup, misal: dalam pemaknaan untuk mencari keridhoan Allah SWT, maka diperlukan keihklasan, maka akan mendapatkan hasil yang tak terhingga.

3. Algoritma. Algoritma secara singkat dapat didefinisikan sebagai Langkah-langkah Sistematis dan Logis dalam menyelesaikan suatu masalah. Dengan konsep Algoritma maka suatu permasalahan harus diselesaikan secara Sistematis, Logis dan bisa diuji benar atau salahnya. Karena Algoritma adalah sebuah konsep, maka tentu setiap orang bisa mempunyai Algoritma yang berbeda-beda terhadap masalah yang sama. Contoh ada suatu permasalahan X dan solusinya adalah Y, maka tiap orang bisa mendapatkan Y dengan Algoritma mereke masing-masing, tidak harus sama akan tetapi menghasilkan output yang sama yaitu Y. Pada prakteknya penerapan Algoritma haruslah efisien. Efisien disini artinya Cepat, Tepat dan Simple. Seperti kasus membuat Software komputer, Software yang dibuat dengan Algoritma yang baik akan menghasilkan software yang efisien, tidak banyak bugs dan tidak makan banyak memory yang tidak perlu misalnya.

4. Model Komputasi. Ada tiga model dasar komputasional yaitu fungsional, logika, dan imperatif. Sebagai tambahan terhadap satuan nilai-nilai dan operasi yang berhubungan, masing-masing model komputasional mempunyai satu set operasi yang digunakan untuk menggambarkan komputasi. Model Fungsional : terdiri dari satu set nilai-nilai, fungsi-fungsi dan operasi aplikasi fungsi dan komposisi fungsi. Fungsi dapat mengambil fungsi lain sebagai argumentasi dan mengembalikan fungsi sebagai hasil (higher-order function). Suatu program adalah koleksi definisi fungsi-fungsi dan suatu komputasi adalah aplikasi fungsi. Model Logika terdiri dari satu set nilai-nilai, definisi hubungan dan kesimpulan logis. Program terdiri dari definisi hubungan dan suatu komputasi adalah suatu bukti(suatu urutan kesimpulan). Model Imperatif terdiri dari satu set nilai-nilai yang mencakup suatu keadaan dan operasi tugas untuk memodifikasi pernyataan. Pernyataan adalah set pasangan nilai-nama dari konstanta dan variabel. Program terdiri dari urutan tugas dan suatu komputasi terdiri dari urutan pernyataan.

5. Eksekusi (Menjalankan Model Simulasi). Dalam menjalankan model simulasi perlu mengikuti model ilmiah yang dapat dapat diterima oleh akal. Hal tersebut dilalkukan dengan model-model analisis yang didasarkan pada kaidah teori.

6. Hasil Perhitungan. Untuk mendapatkan hasil yang baik, model tersebut dibuat sederhana. Semakin sederhana model tersebut, maka akan semakin baik dan memudahkan dalam membangun sebuah model penyelesaian permasalahan yang sedang dibuat. Apabila hasil yang dihasilkan tidak memenuhi kaidah yang ada, maka diperlukan feed back untuk menelaah apakan terjadi kesalahan pada asumsi awal (hiphotesis) atau pada konsep model matematikanya sampai didapatkan hasil yang benar. Misal dalam penyusunan model pondasi rumah, diperlukan teori yang mendukung, seperti perlu diketahui bagaimana beban yang akan bekerja (displacement), bagaimana regangan (elongation) yang akan terjadi yang didasarkan pada tegangan (Stress). Untuk mewujudkan hal tersebut: diperlukan konsep berfikir yang rasional pada kondisi yang terhingga (Finite).

7. Laporan hasil. Laporan yang disajikan hendaknya dilakukan dengan mempertimbangkan fenomena secara ilmiah dan kondisi nyata dilapangan, sehingga akan dapat menghasilkan data yang komprehensif, melalui hasil verifikasi dan validasi. Verifikasi adalah pengujian atau memeriksa model matematika secara benar. Validasi adalah apakah model persamaan yang digunakan sudah benar.

Untuk mewujudkan hal tersebut, dilakukan dengan berbagai program software seperti EES (Engineering Equation Solver)

Pembelajaran Komputasi

Pembelajaran komputasi teknik, didasarkan pada fenomena-fenomena alam secara nyata, melalui pengembangan dari data permasalahan dengan perhitungan-perhitungan dengan pedoman teori yang relevan. Oleh karena itu diperlukan:

1. Data. Data adalah bagian paling dasar/kecil dari karya manusia yang bersifat kaku. Data merupakan representasi dari fakta yang ditemukan dalam aktivitas sehari-hari.

2. Informasi.Informasi adalah sesuatu yang kita bagi melalui beragam media komunikasi yang ada. Informasi : hasil pengolahan dari data yang dapat memberikan gambaran lebih jelas terhadap sesuatu. Informasi bersifat dinamis. Semua orang memiliki tanggapan yang berbeda-beda pada suatu informasi.

3. Pengetahuan. Pengetahuan adalah informasi yang diinterpretasikan dan diintegrasikan. Pengetahuan berasal dari informasi yang diserap dalam akal pikiran seseorang. Pengetahuan bersifat transenden.

4. Ilmu. Ilmu adalah pengetahuan yang bersifat umum dan sistematis, pengetahuan dari mana dapat disimpulkan dalil – dalil tertentu menurut kaidah – kaidah umum. Konsepsi ilmu pada dasarnya mencakup tiga hal yaitu adanya rasionalitas, dapat digeneralisasi dan dapat disistematisasi.

5. Hikmah. secara etimologi bahasa, hikmah berarti kebijaksanaan, pendapat atau pikiran yang bagus. Hikmah merupakan ilmu yang disertai amal (perbuatan), atau perkataan yang logis dan bersih dari kesia-siaan.

Konsep Infinite

Pendahuluan

Konsep tak berhingga (Infinity) adalah sebuah konsep abstrak yang menggambarkan sesuatu yang tanpa batas dan relevan dalam sejumlah bidang, terutama bidang matematika, fisika dan berbagai ilmu turunannya seperti komputasi teknik. Komputasi teknik merupakan satu dari berbagai ilmu yang dikembangkan untuk menjadi bagian dari penyelesaian berbagai persoalan yang dimaksudkan untuk memudahkan dan meyederhanakan permasalahan yang komplek. Konsep berfikir infinite berawal dari penolakan Spinoza (1967) tentang pemikiran Rene Descartes (1957), yaitu res cogitan (hal yang ada di dalam rasio) dan res extensa (hal yang berada di luar rasio), dimana Rene Descartes (1957) berpendapat bahwa Tuhan berada diluar rasio manusia. Hal itulah yang ditolak karena menurut Spinoza (1967) Tuhan berada dalam diri manusia. Pendapat tersebut memberikan dampak pada pengucilan Spinoza dari jemaat gereja, karena dengan pemahaman itu, Spinoza (1967) mengembangkan pemikirannya dan berpendapat bahwa agama yang mapan seperti Yahudi dan Kristen hanya dihidupkan oleh dogmatis dan ritual lahiriah. Secara umum pendapat Spinoza adalah konsep Infinity dari Tuhan, dengan kata lain bahwa Tuhan memiliki sifat infinity. Hal tersebut dapat dijelaskan bahwa sifat Tuhan yang infinity itu, sebuah makna yang subtantif akan rahmat Tuhan yang tidak berhingga kepada seluruh makhluk-NYA. Analoginya adalah, jika diambil himpunan bilangan real, bilangan real tidak terbatas (infinite), jika diambil salah satu sifatnya, misalkan bilangan cacah, maka anggota bilangan cacah akan infinite juga. Oleh sebab itu dapat disimpulkan bahwa kebesaran Tuhan dengan menurunkan salah satu sifatnya, akan mendapatkan gambaran sifat yang infinite juga. Termasuk juga dalam konsep infiniti dalam pembelajaran komputasi teknik, maka dengan sifat Tuhan yang infiniti, maka akan memberikan cara berfikir yang infiniti terhadap penyelesaian berbagai persoalan.

Pembahasan

Dengan menggunakan metodologi penyelesaian masalah dengan tinjauan dari berbagai litratur yang relevan dapat dijelaskan bahwa manusia merupakan makhluk yang paling sempurna yang telah diciptakan oleh Allah (Tuhan YME) dibandingkan dengan makhuk lainnya. Manusia merupakan makhluk Allah (Tuhan YME) yang diciptakan memiliki cipta, rasa dan karsa, yang tidak dimiliki oleh makhluk lainnya. Dengan cipta, manusia akan mampu mendesain berbagai benda yang dapat memberikan kemudahan bagi kegiatan hidupnya. Dengan rasa akan mampu membedakan berbagai hal baik manis, pahit, dll. Serta dengan sifat karsa akan mampu memberikan kreasi terhadap berbagai persoalan yang dihadapinya. Dihadapkan dengan berbagai persoalan konspe inifinite tersebut, menurut Ishartono (2015) ada beberapa poin yang dapat dimaknai dari pendapat Spinoza yaitu: (1) Spinoza melihat segala sesuatu dari perspektif keabadian (sub speciaeternitas). Maksudnya bahwa manusia hanya menjalani kehidupan yang sangat kecil dari begitu besarnya kehidupan itu sendiri (keabadian waktu). (2) Tuhan adalah segalanya, segalanya ada pada diri Tuhan. Bagi Spinoza, Tuhan tidak menciptakan dunia agar dapat berdiri diluar dunia itu sendiri, melainkan Tuhan adalah dunia itu sendiri. (3) Alam bukan hanya segala bentuk alam yang berwujud materi, tetapi segala hal yang bertautan dan ada di alam itu sendiri, bahkan termasuk ruhaniah manusia. Spinoza mengatakan bahwa “Yang Tak Berhingga” (Tuhan dan Alam) merupakan satu dan merupakan segala-galanya. Sedangkan yang disebut berhingga” (gejala-gejala dan benda-benda di dunia) hanya bisa berada dan hanya bisa dipikirkan berkat keberadaan Yang Tak Berhingga. Spinoza kemudian membuat pembedaan di dalam Alam dan Tuhan. Spinoza (1967) menggunakan istilah “Natura naturans” dan “Natura naturata”. Natura naturans adalah Tuhan yang Esa “atau” Alam sebagai asal-usul atau pencipta yang asli. Sedangkan natura naturata adalah ciptaan Tuhan atau Alam yang kelihatan yang menggambarkan akan penciptanya. Dalam konteks pemahaman itu, manusia dimengerti sebagai cara berada “dari” Yang Tak Berhingga. Dan tugas manusia adalah berusaha melihat dengan mata rasionya bahwa segala sesuatu di dunia ini merupakan manifestasi dari Allah (Tuhan YME). Dengan demikian manusia tidak mempunyai kemungkinan lain untuk bertindak selain “harus” melihat semua pengalaman dan segala sesuatu yang ada di dunia ini sebagai substansi yang satu, yaitu Allah (Tuhan YME). Menurut Siswanto (1995) bahwa akal budi dan bahasa sehari-hari selalu cenderung untuk mengadakan pemilahan-pemilihan. Dengan demikian bahwa dengan pembelajaran komputasi teknik tersebut akan memberikan makna akan sifat infinite Allah (Tuhan YME), sehingga akan mampu menjadikan sebagai makhluk Allah yang lebih tawadhu dalam menyelesaikan berbagai persoalan yang dihadapinya.

Kesimpulan

Dari penjelasaan yang telah diuraikan diatas dapat disiimpulkan sebagai berikut:

1. Manusia merupakan makhluk Allah (Tuhan YME) yang paling sempurna dengan dianugerahi oleh-NYA cipta, rasa dan karsa sebagai pemimpin di dunia.

2. Sebagai manusia diharapkan dalam melihat suatu permaslaahan dalam kehidupan dari pembagian dimensi waktu yaitu pra, proses, dan pasca secara seksama atas kehendak Allah (Tuhan YME), sehingga manusia hendaknya agar lebih bijak dalam mensikapi berbagai permasalahan. Atau dengan kata lain, dunia itu ada “dalam” diri Allah (Tuhan YME) itu sendiri.

3. Allah (Tuhan YME) “Yang Tak Berhingga” (Tuhan dan Alam) merupakan yang satu dan merupakan segala-galanya. Sedangkan yang disebut berhingga” (gejala-gejala dan benda-benda di dunia) itu hanya bisa berada dan hanya bisa dipikirkan berkat keberadaan Yang Tak Berhingga.

4. Dengan makna akan konsep infinite dan dihadapkan pada mata kulaih komputasi teknik akan lebih mendekatkan manusia lebih tawadhu akan sifat Allah (Tuhan YME) yang infinite.

Referensi.

Descartes, R., 1957, A Discourse on Method, translated by Iohn Veitch, I.M. Dent"& Sons Ltd., London

Ishartono, Naufal, 2015, Filsafat Pendidikan Matematika Review dari Beberapa Preposisi di dalam Ethics Book oleh Spinoza, Universitas Muhammadiyah Surakarta.

Spinoza, B., 1967, Ethics, J.M. Dent & Sons Ltd., London

Siswanto, Joko, 1995, Metafisika Substansi, Universitas Gadjah Mada, Jurnal filsafat Mei '95

Perhitungan Fungsi

Jika terdapat persamaan f(y)= ((X^2-1))/((X-1)), dengan nilai x=1, bila dalam penyelesaian sebuah fungsi dengan hasil nol, maka penyelesaian dilakukan dengan menggunakan limit (Andi Hakim Nasution dkk, 1994). hasil nol tersebut lebih lanjut dapat diuraikan sebagai berikut:

F(y)= ((X^2-1))/((X-1)) = ((1^2-1))/((1-1))= 0/0 bukan merupakan nilai (tidak terdefinisi), sehingga diperlukan penyelesaian dengan metode lain yang meliputi:

1. Metode pemfaktoran limit fungsi.

Dengan alasan bahwa untuk medapatkan hasil nilai x yang mendekati 1, dengan penyelesaian sebagai berikut:

= lim (X→1)=⁡((X^2-1))/((X-1))

=lim (X→1)⁡ = (X+1)(X-1))/((X-1))), menjadi

= x+1

= (1+1)

= 2

Metode limit dalil L’Hospital

Bernard V. Zandy dan Jonathan J. White, (2004), dengan dalil L’Hospital dapat dilakukan untuk menyelesaikan limit pembagian fungsi f(x)/g(x) yang tidak terdefinisi. Dengan kata lain jika f(x)/g(x) = 0 atau tak terhingga, maka limit pembagian fungsi dapat dilkukan dengan penyelesaian fungsi limit hasil bagi turunannya. Dimana dalam penyelesaian dengan metode L’Hospital, dapat dijelaskan sebagai berikut:

= 〖 lim〗┬(X→1)⁡〖(f (x))/(g(x))〗 = 〖 lim〗┬(X→1)⁡〖(f' (x))/(g'(x))〗

= 〖 lim〗┬(X→1)⁡〖((X^2-1))/((X-1) )〗 =〖 lim〗┬(X→1 )⁡〖2X/1〗

= ((2.1))/((1))

= 2

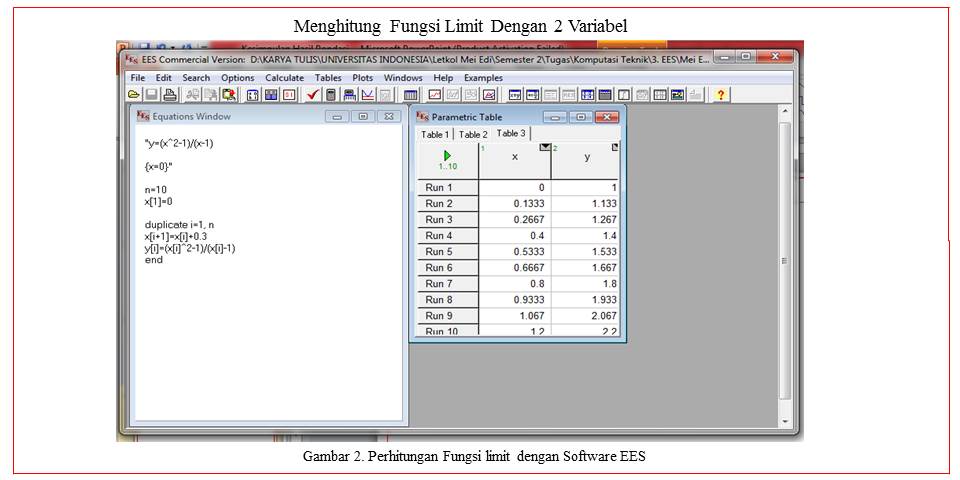
Menggunakan Software EES

Dengan memasukkan variabel yang akan dicari dengan formulasi yang telah diberikan, maka dapat diketahui solusi seperti gambar 2, sebagai berikut:

Referensi

Andi Hakim Nasution dkk, 1994, Matematika 2, Departemen Pendidikan dan Kebudayaan, Jakarta.

Bernard V. Zandy dan Jonathan J. White, 2004, Cliffs Quick Review TM Calculus, Pakar Raya, Bandung.

Pemodelan Matematika

Ada tiga model dasar komputasional: fungsional, logika, dan imperatif. Sebagai tambahan terhadap satuan nilai-nilai dan operasi yang berhubungan, masing-masing model komputasional mempunyai satu set operasi yang digunakan untuk menggambarkan komputasi. Menurut yunus (2012), ada tiga model matematika:

1. Model Fungsional. Model ini terdiri dari satu set nilai, fungsi, dan operasi aplikasi fungsi dan komposisi fungsi. Fungsi ini dapat mengambil fungsi lain sebagai argumentasi dan mengembalikan fungsi tersebut sebagai hasil (higher-order function). Suatu program adalah kumpulan definisi fungsi sedangkan suatu komputasi adalah aplikasi fungsi. Contoh model fungsional : Fungsi linier y = 3x + 2 dapat didefinisikan sebagai berikut fx = 3*x + 2.

2. Model Logika. Model ini menjadi sangat penting karena telah dikembangkan dari ratusan tahun yang lalu dan sebagai bentuk metode dasar dari sebagian besar metode penyelesaian masalah. Model ini terdiri dari satu set nilai, definisi hubungan, dan kesimpulan logis. Program terdiri dari definisi hubungan dan suatu komputasi adalah suatu bukti (suatu urutan kesimpulan). Contoh model logika : Fungsi linier y = 3x + 2 dapat didefinisikan sebagai berikut F(X,Y) if Y is 3*x + 2. Model logika penting karena merupakan perumusan proses pemberian alasan dan itu berhubungan dengan relatioanl database dan expert system.

3. Model Imperatif. Model ini terdiri dari satu set nilai yang mencakup suatu keadaan dan operasi tugas untuk memodifikasi pernyataan. Pernyataan adalah set pasangan nilai-nama dari konstanta dan variabel. Program terdiri dari urutan tugas dan suatu komputasi terdiri dari urutan pernyataan. Contoh model imperatif : Fungsi linier y = 2x + 3 dapat didefinisikan sebagai berikut y:= 2*x +3. Model imperatif penting karena model berubah dan perubahan adalah bagian dari lingkungan. Model imperatif merupakan pendekatan yang paling tepat untuk pemodelan perangkat keras yang mengeksekusi program.

Konsep Model Persamaan Matematika Pondasi Rumah Panggung

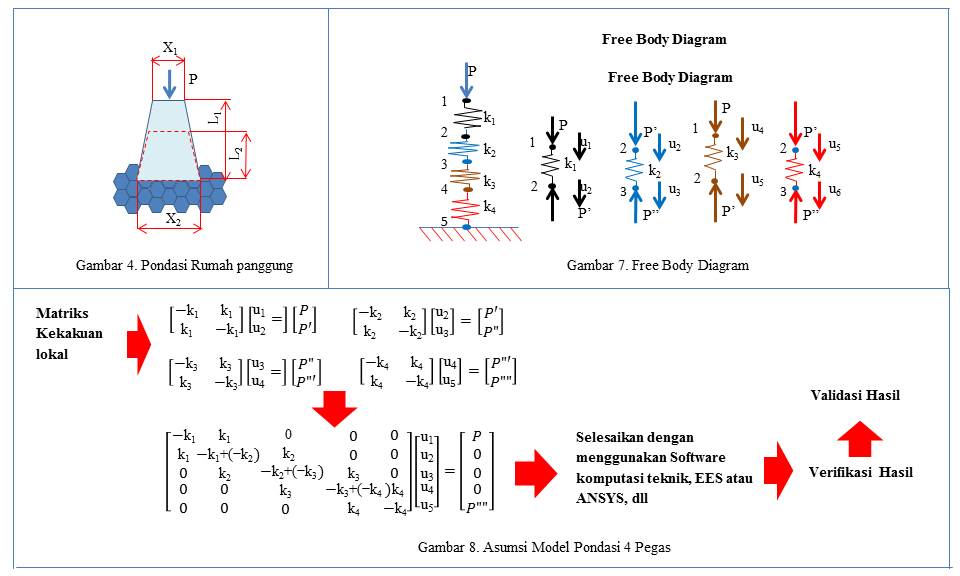
Untuk menghitung displacement (u), regangan (ε) dan tegangan (σ) dengan asumsi gaya yang bekerja (P) pada sebuah pondasi rumah panggung seperti pada gambar 1. diperlukan sebuah asumsi dengan prosedur sebagai berikut:

1. Menentukan masalah (problem). Dalam menentukan akar permasalahan adalah untuk menghitung berapa nilai displacement (u), regangan (ε) dan tegangan (σ) dengan asumsi sebuah pondasi yang mendapatkan gaya sebesar F.

2. Asumsi/Pemikiran awal (analisis awal). Diasumsikan bahwa sebuah pondasi dengan material homogen mendapatkan gaya vertikal ke bawah seperti gambar 1 sebesar F. sebagai akibat adanya gaya sebesar F, maka pondasi akan mengalami perubahan searah dengan gaya.

3. Algoritma. Untuk menghitung nilai displacement (u), regangan (ε) dan tegangan (σ) diperlukan pendekatan model pegas sederhana 1 dimensi karena gaya yang bekerja pada satu sumbu yang sama. Sesuai Persamaan (1), (2), (3), (4) dan (5).

4. Model Komputasi. Model komputasi pada sebuah pondasi yang mendapatkan beban diasumsikan sebagai sebuah pegas, seperti pada gambar 1, gambar 2 dan Gambar 3.

5. Eksekusi / Jalankan model (Simulasi).Dengan melakukan model dalam komputasi teknik menggunakan program Engineering equation Solver (EES)

6. Hasil Perhitungan. Hasil perhitungan dilakukan dengan melaksanakan verifikasi/validasi struktur

7. Laporan Hasil. Dari hasil penghitunag dapat disusun laporan.

Model Matematika Pondasi Rumah Panggung

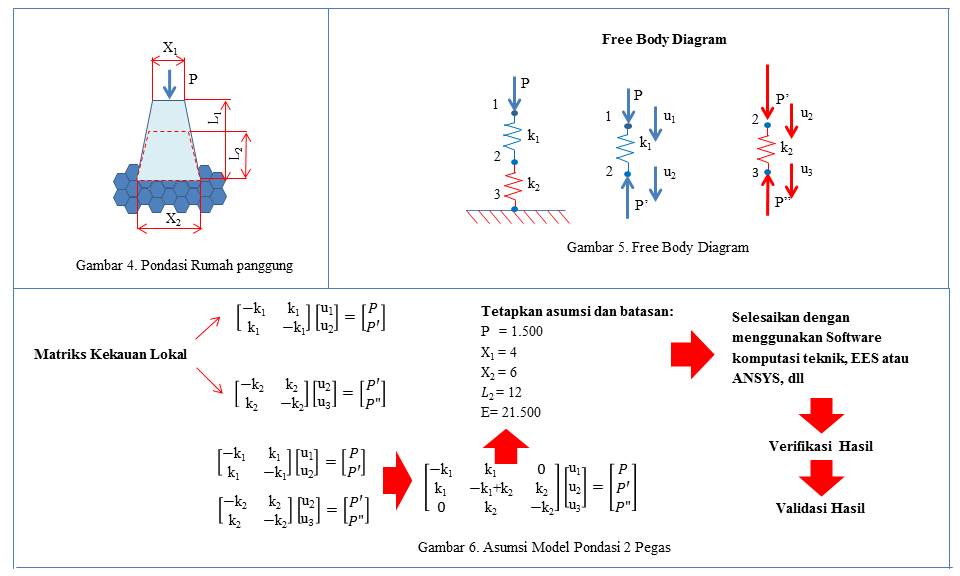
Dalam model matematika untuk menghitung displacement (u), regangan (ε) dan tegangan (σ) dengan asumsi gaya yang bekerja (P) pada sebuah pondasi rumah panggung seperti pada gambar 4.

a. Asumsi Pondasi Dengan 2 Pegas.

Diasumsikan pondasi dengan model 2 pegas seperti gambar 5 dan gambar 6, sebagai berikut:

b. Asumsi Pondasi Dengan 4 Pegas.

Diasumsikan pondasi dengan model 4 pegas seperti gambar 7 dan gambar 8, sebagai berikut:

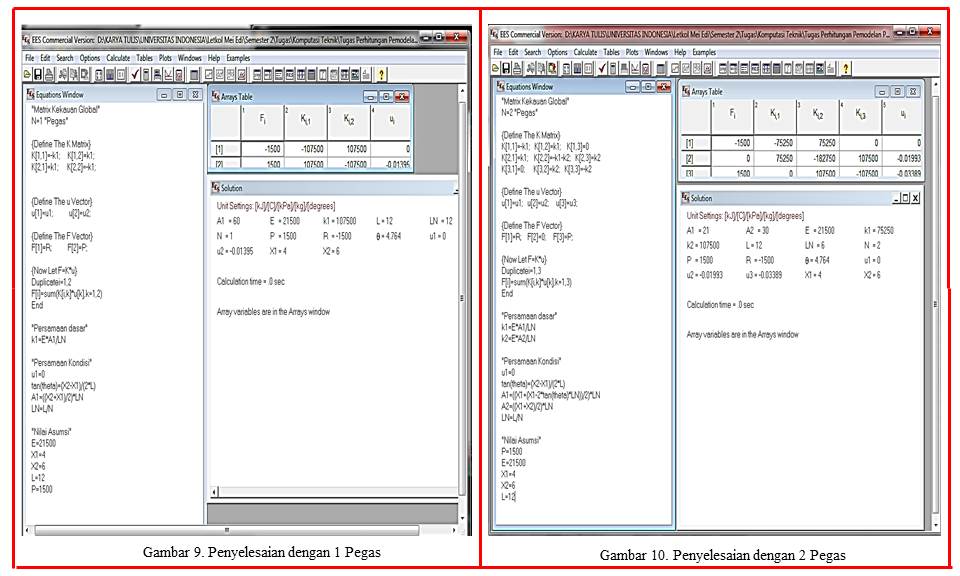
Hasil Perhitungan Model Matematika Pondasi Rumah Panggung (Dengan Pemodelan 1 dan 2 Pegas)

Dalam model matematika untuk menghitung displacement (u), regangan (ε) dan tegangan (σ) dengan asumsi gaya yang bekerja (P) pada sebuah pondasi rumah panggung diasumsikan sebuah model 1 dan 2 pegas ditunjukkan pada gambar 9 dan gambar 10, sebagai berikut:

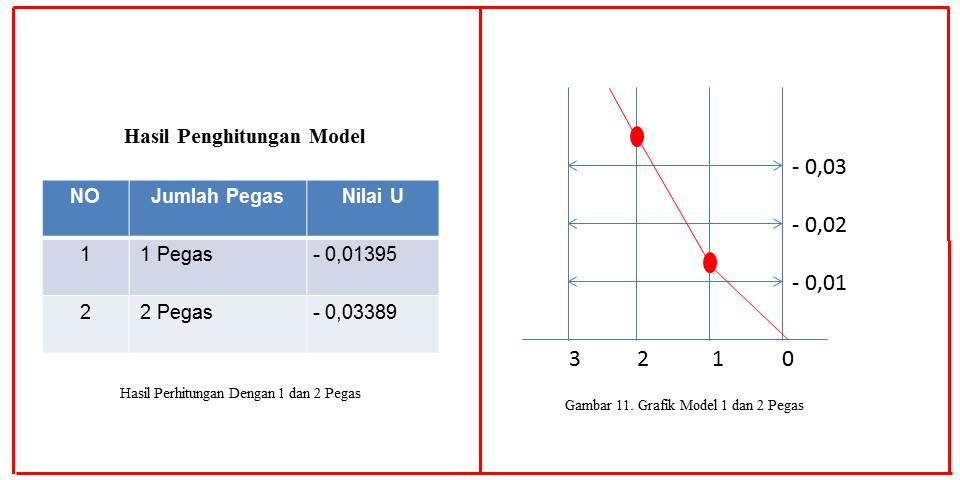
Kesimpulan

Dari hasi perhitungan dengan model 1 pegas dan 2 pegas dapat disimpulkan sebagai berikut:

a. Terdapat kenaikan nilai u akhir pada setiap pertambahan jumlah pegas. Oleh karena itu diperlukan tahap validasi untuk menentukan persamaan yang tepat digunakan.

b. Tahap validasi dilakukan dengan membandingkan persamaan yang didapat dengan hasil eksperimen.

Analisa Biaya pembangunan Rumah Toko Sebagai Tempat Usaha

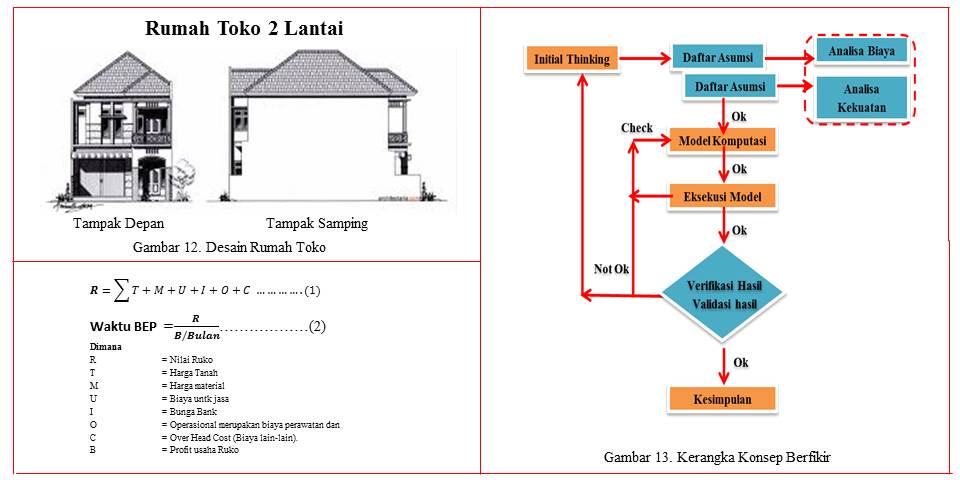
Pembangunan rumah toko merupakan konsep pembangunan rumah toko yang diharapkan akan mampu memberikan hasil optimal dalam pengembalian modal (beak event point- BEP). Pembangunan rumah toko diasumsikan memiliki 2 lantai yang berfumgsi sebagai rumah sekaligus toko, dimana pada lantai 1 dipergunakan sebagai toko dan lantai 2 sebagai rumah, seperti pada gambar 12. Adapun diasumsikan bahwa rumah toko tersebut, dengan ukuran 5 x 8 M = 40 M2, Total 80 M2, dengan struktur pembangunan adalah pembuatan Pondasi, Slope, Dinding, bangunan lantai 1 dan lantai 2, bangunan lantai 1 dan lantai 2, struktur kerangka atap dan atap terbuat dari genting.

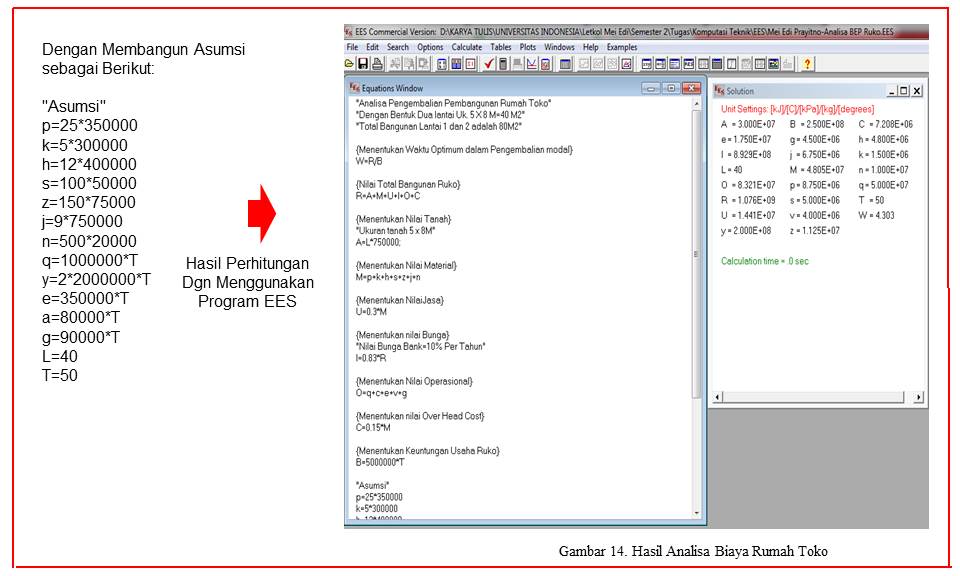
Adapun konsep analisis dengan menggunakan software EES adalah sebagai berikut:

1. Menentukan masalah (problem). Dalam menentukan akar permasalahan adalah untuk menghitung berapa waktu pengembalian dari analisis biaya pembangunan rumah toko tersebut.

2. Asumsi/Pemikiran awal (analisis awal). Diasumsikan bahwa dalam pembangunan rumah toko tersebut biaya yang dikeluarkan diperuntukkan: Harga tanah = Rp 750.000,00/M2. Material rumah terdiri dari beberapa jenis material pasir (p), batu kali (k), hebel (h), semen (s), baja ringan (z), kayu untuk pintu (j) dan atap genting (n). Jasa untuk pembangunan, besarnya 30% dari material bangunan. Bunga bank (interest rate ) sebesar 10% /Tahun. Operarional adalah penjumlahan dari nilai Perawatan (r), Upah karyawan (w), Listrik (e), Air (v) dan Gas (g). Over head Cost adalah biaya yang timbul diluar dugaan besarnya 15% dari harga material.

3. Algoritma. Untuk menghitung berapa waktu untuk pengembalian dalam pembangunan rumah toko tersebut adalah besarnya biaya pembangunan rumah toko, dibagi dengan besarnya pendapat dari usaha toko tersebut. Adapay secara algirtma dapat ditunjukkan pada persamaam (1) dan persamaan (2).

5. Eksekusi / Jalankan model (Simulasi). Dengan melakukan model dalam komputasi teknik menggunakan program Engineering equation Solver (EES)

6. Hasil Perhitungan. Hasil perhitungan dilakukan dengan melaksanakan verifikasi terhadap hasil perhitungan baiaya

7. Laporan Hasil. Dari hasi perhitungan setelah dilkukan verifikasi dan validasi hasil dapat dilakukan pelaporan.

Perhitungan Biaya pembangunan Rumah Toko Sebagai Tempat Usaha (Quiz 1)

Model Persamaan Matematika

Langkah Pertama dalam komputasi teknik adalah Menyusun Persamaan Matematika, sebagai Berikut:

"Analisa Pengembalian Pembangunan Rumah Toko"

"Dengan Bentuk Dua lantai Uk. 5 X 8 M=40 M2"

"Total Bangunan Lantai 1 dan 2 adalah 80M2"

{Menentukan Waktu Optimum dalam Pengembalian modal} W=R/B

{Nilai Total Bangunan Ruko} R=A+M+U+I+O+C

{Menentukan Nilai Tanah} "Ukuran tanah 5 x 8M" A=L*750000;

{Menentukan Nilai Material} M=p+k+h+s+a+j+n

{Menentukan NilaiJasa} U=0.3*M

{Menentukan nilai Bunga} "Nilai Bunga Bank=10% Per Tahun" I=0.83*R

{Menentukan Nilai Operasional} O=q+w+e+a+g

{Menentukan nilai Over Head Cost} C=0.15*M

{Menentukan Keuntungan Usaha Ruko} B=5000000*T

"Asumsi"

Dengan Asumsi sebagai Berikut:

p=25*350000

k=5*300000

h=12*400000

s=100*50000

z=150*75000

j=9*750000

n=500*20000

q=1000000*T

y=2*2000000*T

e=350000*T

a=80000*T

g=90000*T

L=40

T=50

Hasil

Dari hasil pengolahan data dengan menggunakan metode EES didapatkan hasil sebagai berikut:

Kesimpulan:

Dari hasil pengolahan data dapat disimpulkan sebagai berikut:

a. Rumah toko yang digunakan untuk sebuah usaha diasumsikan menghasilkan keuntungan sebesar Rp. 15.000.000,-

b. Dengan Asumsi keuntungan sebesar Rp 15.000.000,- dapat dihitung lama waktu BEP (break event point) adalah selama 50 Bulan

Analisis Struktur Kekuatan Rumah Toko (2D)

Telah dijelaskan pada bab-bab sebelumnya bahwa direncanakan akan membangun rumah toko, dengan ukuran 6 x 9 meter, dua lantai. untuk dapat menghitung kekuatan struktur bangunan dapat digunakan berbagai software pendukung seperti structure analysis program (SAP) maupun Framework. sebagai asumsi dari kondisi bangunan dapat dijelaskan bahwa tinggi lantai 1 = 3,5 m. tinggi lantai 2 = 3,5m dan tinggi atap = 3m. Adapun bangunan rumah toko dibuat menjadi 4 blok pada masing-masing lantai. Asumsi semua desain kontruksi dan struktur beban pada masing-masing titik (Nodes) seperti data pada link https://drive.google.com/file/d/1IDFHFPxAO5FMPANVE8RrfVkfhCtK11-W/view?usp=sharing.

Hasil pengolahan data dengan menggunakan software Framework untuk kondisi 2D dapat dilihat pada link https://drive.google.com/file/d/1shIHjR2jge_Jsinw09e97dZrBCwGqYqa/view?usp=sharing, sedangkan hasil pengolahan gambar dengan software Gnuplot dapat dilihat pada link https://drive.google.com/file/d/1qWegx4c3oyQUPJ1iisCKXkTkTsrU8k90/view?usp=sharing

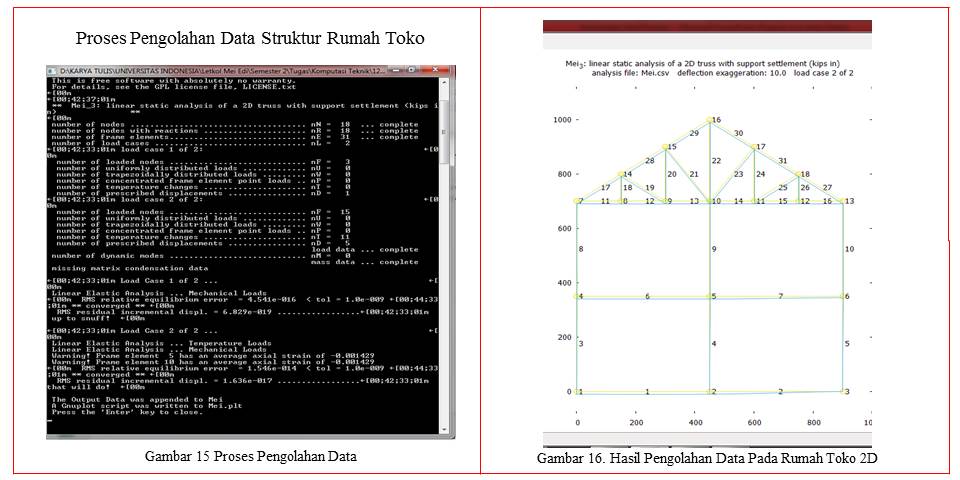
Dari pengolahan data tersebut dapat dilihat hasil pengolahan dapat pada gambar 15 dan gambar 16 sebagai berikut:

Kesimpulan.

Dari hasil asumsi gaya yang bekerja pada setiap nodes, dapat disimpulkan sebagai berikut:

a. Gaya pada sumbu x terdapat pada Node 4 sebesar 59,998 kip dan Node 7 sebesar 95,00 kip.

b. Besarnya gaya lokal yang bekerja pada masing-masing Elemen yang memiliki nilai maksimum maupun minimum ada pada elemen 28 sebesar 23,52 kip dan Elemen 5 sebesar (-414,286) kip (info data link https://drive.google.com/file/d/1shIHjR2jge_Jsinw09e97dZrBCwGqYqa/view?usp=sharing).

Analisis Kekuatan Struktur Rumah Toko (3D)

Dari hasil pengolahan data yang telah dilakukan pada penugasan sebelumnya dilanjutkan dengan analisis beban pada kondisi 3D pada sebuah rumah toko dengan ukuran 6 x 9 meter, dua lantai dan atap dengan struktur kontruksi seperti gambar 16 di atas. Untuk dapat menghitung kekuatan struktur bangunan pada kondisi 3D digunakan software Framework. Sebagai asumsi dari kondisi bangunan dapat dijelaskan bahwa tinggi lantai 1 = 3,5 m. tinggi lantai 2 = 3,5m dan tinggi atap = 3m. Adapun bangunan rumah toko dibuat menjadi 4 blok pada masing-masing lantai. Data rumah toko diasumsikan rumah toko dengan ukuran dan kondisi sebagai berikut:

Uk : 6 x 9m

Jumlah Node : 30 Node

Jumlah Elemen : 60 Elemen

Jumlah Beban Uniform : 6

Jumlah Animasi : 5

Asumsi semua desain kontruksi dan struktur beban pada masing-masing titik (Nodes) seperti data pada link https://drive.google.com/open?id=1slXIBlkcXgqftyxjrgi1vevizjAt1gQp

Hasil pengolahan data dengan menggunakan software Framework untuk kondisi 3D dapat dilihat pada link https://drive.google.com/open?id=1v4AkzEifx1Jy7XoISxt4qp1aAJkAh_qI.

Hasil pengolahan berupa gambar dengan software Gnuplot dapat dilihat pada https://drive.google.com/open?id=1e15qSEyXaErb09OfS-aRv5hJIRjn1T-D.

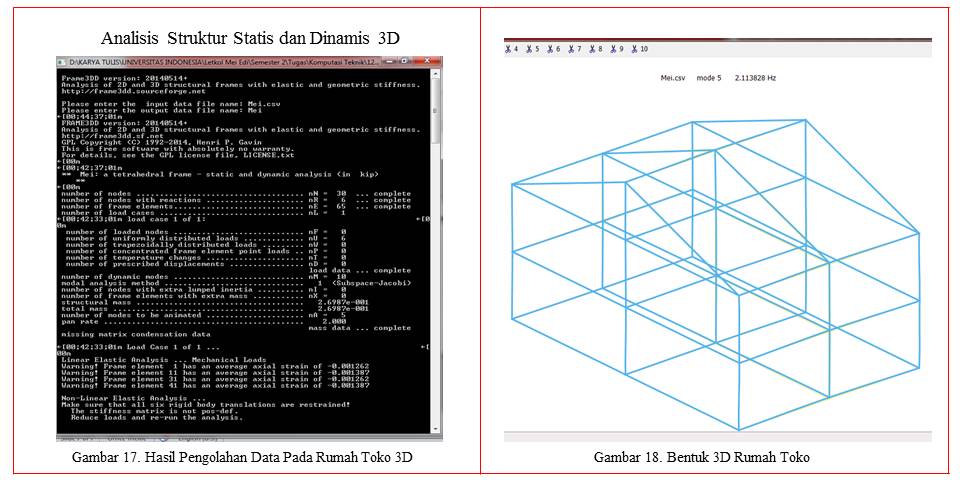
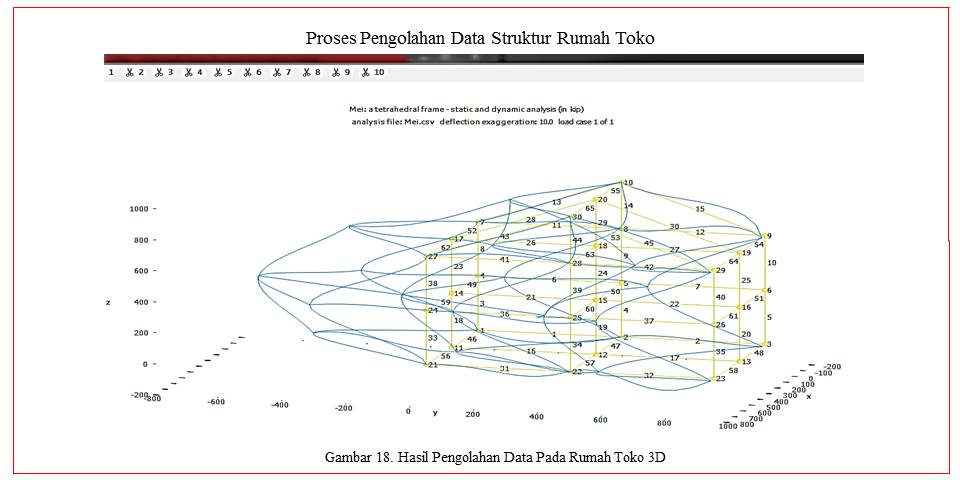
Dari pengolahan data tersebut dapat dilihat hasil pengolahan dapat pada gambar 17 dan gambar 18 sebagai berikut:

sedangkan dari hasil pengolahan data gaya-gaya yang bekerja pada struktur bangunan dapat ditunjukkan pada gambar 19 sebagai berikut:

Kesimpulan.

Dari hasil asumsi gaya yang bekerja pada setiap nodes, dapat disimpulkan sebagai berikut:

a. Perlu perhatian struktur bangunan pada elemen 1, 11, 31 dan 41, dengan alasan bahwa hasil pengolahan data Elemen 1, rata-rata memiliki strain = -0,001262, Elemen 11, rata-rata memiliki strain = -0,001387, Elemen 31, rata-rata memiliki strain = -0,001262 dan Elemen 41, rata-rata memiliki strain = -0,001387.

b. Hasil pengolahan data secara umum kontruksi mampu menahan beban yang bekerja.

Dinamika Pada Struktur Terhadap Gaya Dari Luar

Dinamika Beban

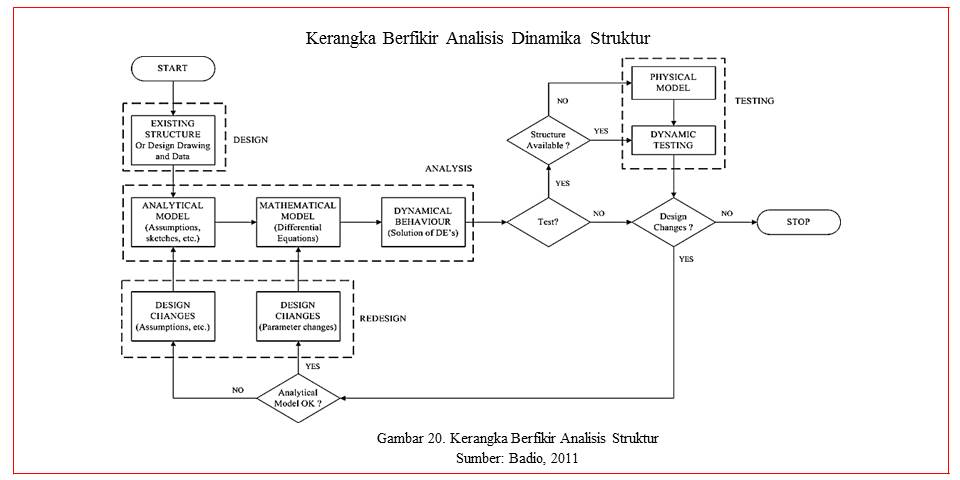
Dinamika merupakan suatu keadaan dimana perubahan pada sebuah elemen terjadi terhadap waktu dalam konteks gaya yang bekerja pada struktur tersebut. Beban dinamis dapat berupa variasi besarnya (magnitude), arahnya (direction) atau posisinya (point of application) berubah terhadap waktu. Sehingga respon struktur terhadap beban dinamik berupa lendutan dan tegangan yang bersifat dinamik menurut beban yang dialaminya [Budio, S. P., 2011]. Adapun perbedaan beban statis dan dinamis terletak pada sumber bebannya dimana lendutan dan tegangan internal dalam kasus beban statis ditimbulkan langsung oleh beban P, sedangkan untuk kasus beban dinamis, percepatan yang dialami oleh sebuah elemen akibat P(t) menimbulkan gaya inersia yang terdistribusi pada seluruh elemen. Apabila pengaruh gaya inersia pada elemen terjadi sangat signifikan maka perlu dilakukan analisa dinamis. Adapun perbedaan perlakuan beban statis dan beban dinamis pada sebuah elemen balok dapat dilihat pada gambar 20 di bawah ini.

Dari bagan alir di atas, dapat dilihat bahwa model analitis terdiri dari:

a. Asumsi-asumsi yang dibuat untuk menyederhanakan sebuah sistem;

b. Gambar dari model analitis tersebut;

c. Parameter desain yang digunakan.

Untuk model analitis dapat dibagi menjadi dua bagian, yaitu:

a. Model berkesinambungan (Continues Model);

b. Model diskrit (Discrete-ParameterModel).

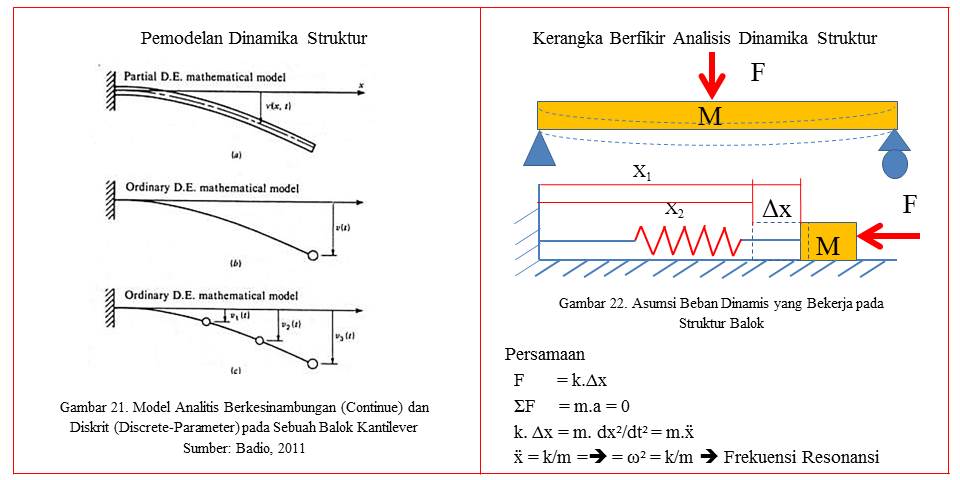
Pada dasarnya, model berkesinambungan (continues model) memiliki jumlah derajat kebebasan [number of Degree of Freedom (DOF)] yang tak terhingga. Namun pada kenyataanya, untuk mempermudah analisa, sebuah model matematis dapat mereduksi jumlah yang tak terthingga tersebut menjadi jumlah yang diskrit, seperti gambar 21.

Perhitungan Beban Dinamis P(t)

Pada sebuah struktur balok yang mendapatkan beban dari luar akan memberikan pengaruh yang diasumsikan sebagai beban yang diberikan pada sebuah pegas. Akibat dari adanya beban tersebut pegas akan memberikan respon bergerak searah dengan beban dan pada batas tertentu akan memberikan respon balik yang pada akhirnya akan berada pada kondisi setimbang (tidak bergerak/beresonansi), seperti pada gambar 22.

Hal yang perlu diperhatikan dalam merencanakan grafik sinus dari beban harmonik ini adalah fase puncak dan lembah sinus. Karena fase puncak sinus terjadi pada saat 1/4π, 5/4π, 9/4π, dan seterusnya dan fase lembah terjadi pada saat 3/4π, 7/4π, 11/4π dan seterusnya sehingga dalam menentukan fase grafik sebaiknya dalam bentuk kelipatan 0,5. Kemudian waktu terjadinya puncak dan lembah diperoleh dari persamaan ω=2π/t (Supartono, 1981).

Persamaan

F = k.Δx ==> Δx =x1-x2

ΣF = m.a = 0

k. Δx = m. dx²/dt² = m.ẍ

ẍ = k/m ==> ω² = k/m ==> Frekuensi Resonansi

Refferensi

Sugeng P. Budio, 2011, Buku Ajar Dinamika danRekayasa Gempa, Univeritas Brawijaya.

Supartono, F.X., Boen, Teddy, 1981, nalisa Struktur dengan Metode Matrix, Jakarta: UI Press.

Analisis Dinamika Pada Struktur Balok (Beam) Rumah Toko

Dinamika Pada Struktur Balok Rumah Toko

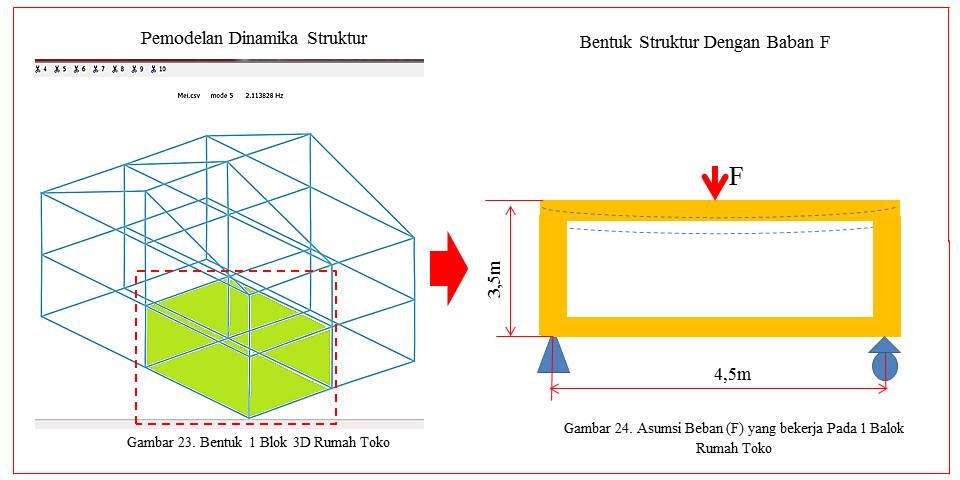
Diasumsikan bahwa struktur balok rumah rumah mendapatkan beban dari luar. Sebagai akibat dari beban tersebut struktur balok akan menahan beban, sehingga terjadi defleksi searah dengan sumber beban/gaya dan akan bergerak berlawanan arah dengan arah beban/gaya pada saat beban/gaya dilepaskan, sehingga dapat diasumsikan seperti bekerjanya sebuah pegas, seperti gambar 22, di atas. Pada pembahasan dinamika pada struktur balok kali ini akan dibahas pada kondisi balok pada 1 blok rumah toko dan 2 blok rumah toko seperti pada gambar 23 sebagai berikut:

Dinamika Pada Struktur 1 Blok - 1 Balok Penahan

Untuk menganalisis bagaimana dinamika yang terjadi pada struktur balok pada kondisi satu blok diasumsikan bahwa panjang balok pada sumbu x adalah 3m, panjang balok pada sumbu y adalah 4m dan panjang kolom adalah 3,5m seperti gambar 24.

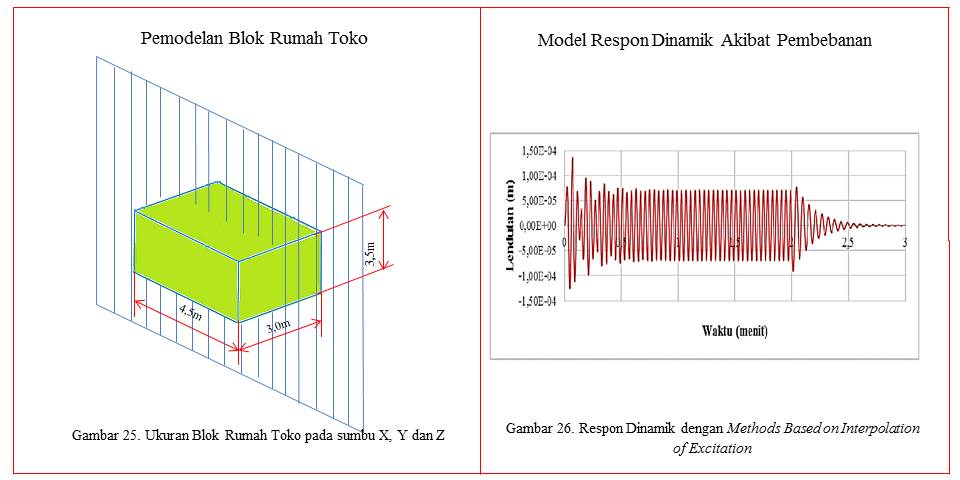
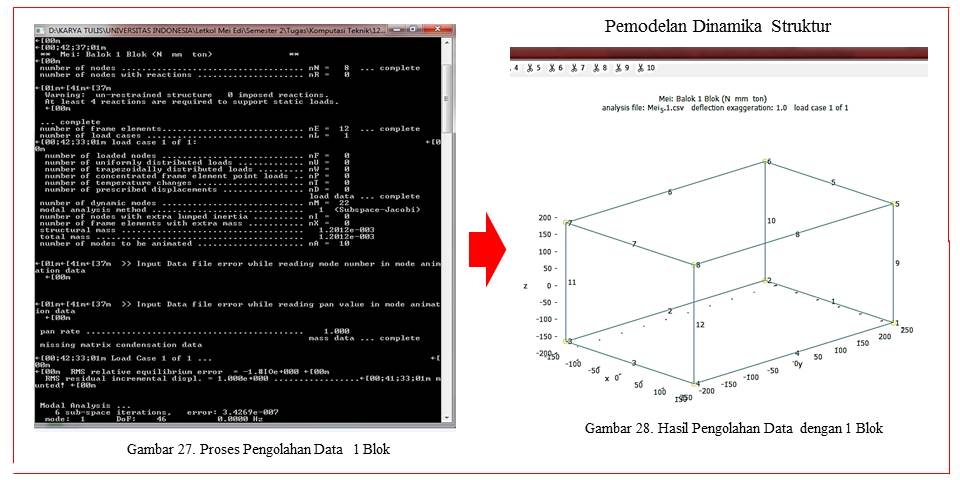
Penyusunan dalam pengolahan data diasumsikan seperti gambar 25, sehingga pada sumbu x noda 1 sepanjang 150cm, noda 2 sepanjang -150cm, noda 3 sepanjang -150cm dan noda 4 sepanjang 150cm. Pada balok 1 blok diasumsikan terdapat 8 blok dan 12 elemen seperti gambar 28. untuk proses input data dapat dilihat pada link berikut; https://drive.google.com/open?id=1rOl6__SBzab0La_a_vIHnu1iIotq2fgH.

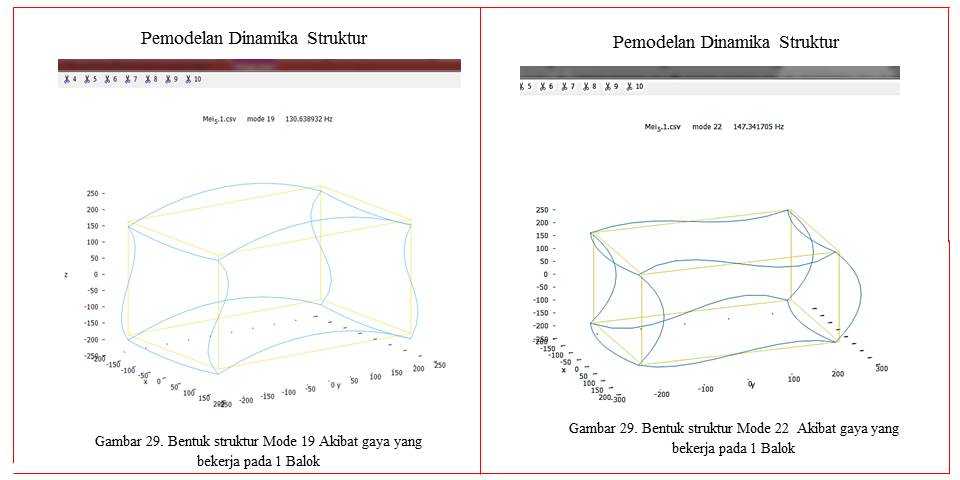
Hasil penginputan data dapat dilihat pada gambar 27. Hasil pengolahan data adalah berupa bentuk blok dengan struktur balok seperti pada gambar 28. Dari hasil pengolahan data dapat dilihat pada link berikut: https://drive.google.com/open?id=1f6gkxAXFPLO-P-nul2EQW-Ae4I_qkZTe. Dari hasil pengolahan data tersebut dapat dilihat pada kondisi 8 animasi dengan tolerasi 0,000001. Hasil pengolahan data dengan 8 model animasi tersebut dapat dilihat pada gambr 29 dan gambar 30 serta secara lengkap dapat dilihat pada link: https://drive.google.com/open?id=1vBLQjl8iWMqmiOrpyVAJyvAcXlz_AKEK.

Dinamika Pada Struktur 2 Blok - 2 Balok Penahan

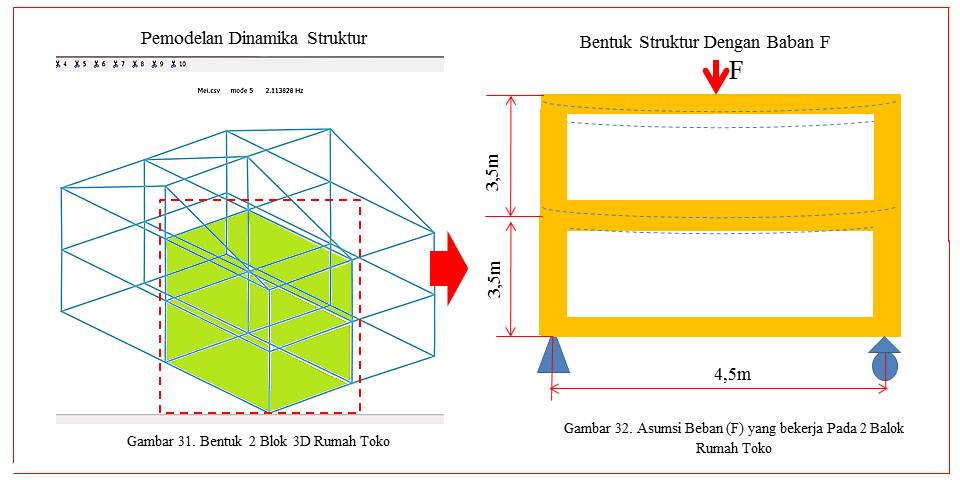
Untuk menganalisis bagaimana dinamika yang terjadi pada struktur balok pada kondisi dua blok diasumsikan terdapat 12 nodas dengan panjang balok pada sumbu x adalah 3m, panjang balok pada sumbu y adalah 4m dan panjang kolom adalah 7m seperti gambar 31 dan gambar 32 berikut.

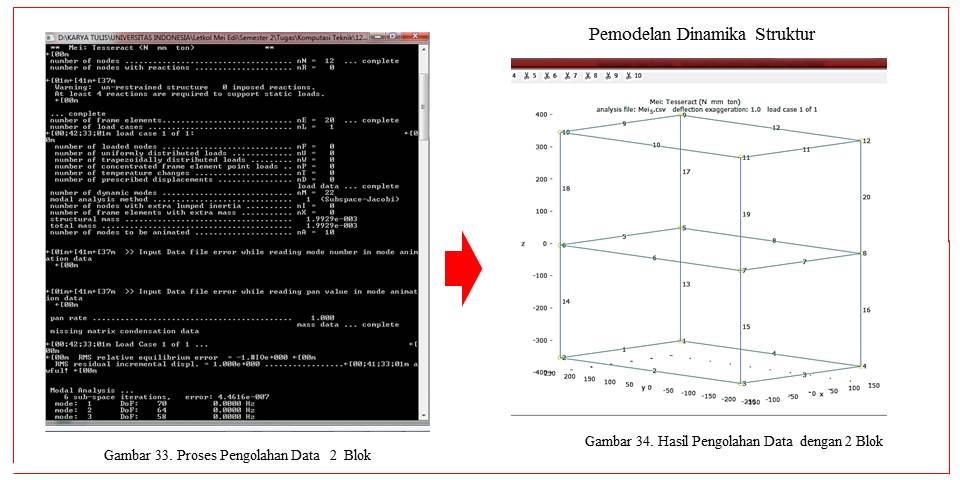
Penyusunan dalam pengolahan data dapat dilihat pada gambar 33. Dari hasil pengimputan data dapat dijelaskan pada sumbu x noda 1 sepanjang 150cm, noda 2 sepanjang -150cm, noda 3 sepanjang -150cm dan noda 4 sepanjang 150cm.Sedangkan pada sumbu z, node 1, 2, 3 dan 4 pada koordinat sepanjang 350cm, Node 5, 6, 7 dan 8 sepanjang 0 cm, sedangkan node 9, 10, 11 dan 12 sepanjang -350cm, seperti gambar 33. Pada balok 2 blok diasumsikan terdapat 12 nodes dan 20 elemen seperti gambar 34. untuk proses input data dapat dilihat pada link berikut: https://drive.google.com/open?id=1uhmBbftNXU1e6tIfvGoxkz7rt6kM5VW7.

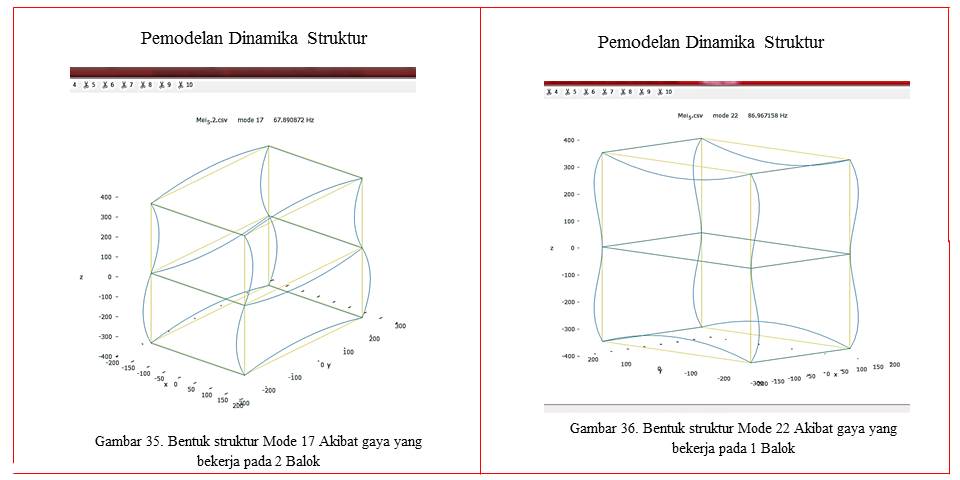
Hasil penginputan data dapat dilihat pada gambar 33. Hasil pengolahan data adalah berupa bentuk blok dengan struktur balok seperti pada gambar 34. Dari hasil pengolahan data dapat dilihat pada link berikut: https://drive.google.com/open?id=1mF6p0K9p33gu-SNKsUmGF33B4jLZf-p5. Dari hasil pengolahan data tersebut dapat dilihat pada kondisi 8 animasi dengan tolerasi 0,000001. Hasil pengolahan data dengan 8 model animasi tersebut dapat dilihat pada gambr 35 dan gambar 36 serta secara lengkap dapat dilihat pada link: https://drive.google.com/open?id=1tgpAuRbWHQU4VhsQJMSvpRMrgL15Z494.

Kesimpulan

Dari pengolahan data dengan kondisi 1 blok dan 2 blok dapat disimpulkan sebagai berikut:

a. Semakin panjang rentang balok, maka tingkat kelendutan akan semakin besar. Untuk meningkatkan kekakuan struktur balok dapat ditingkatkan dimensi balok.

b. Pada struktur balok pada kondisi 1 blok maupun pada kondisi 2 blok, titik terkecil mendapat pengaruh beban/gaya adalah pada titik tengah (netral axis).

Analisis Defleksi Elastisitas Balok (Beam) Rumah Toko (Tugas UTS)

Pendahuluan

Dalam perancangan kontruksi balok, tegangan yang terjadi, sifat penampang dan beban-beban luar dapat diperhitungkan. Pada prinsipnya tegangan pada balok akibat beban luar dapat direncanakan tidak melampaui suatu nilai tertentu, seperti tegangan ijin. Perancangan yang berdasarkan batasan tegangan ini dinamakan perancangan berdasarkan kekuatan (design for strength). Pada umumnya defleksi/lendutan balok perlu ditinjau agar titik melampaui nilai tertentu. Dapat terjadi, dari segi kekuatan balok masih mampu menahan beban, namun lendutannya cukup besar sehingga tidak nyaman lagi. Perancangan yang mempertimbangkan batasan lendutan dinamakan perancangan berdasarkan kekakuan (design for stiffhess). Lendutan balok pada umumnya diakibatkan oleh momen lentur dan gaya geser secara bersamaan. Lendutan balok yang diakibatkan oleh momen lentur lebih dominan dibandingkan oleh momen geser. Pada uraian di bawah akan dibahas beberapa cara perhitungan lendutan balok akibat lentur antara lain:metode integrasi ganda (double integration), metode luas momen (momen area) dan metode superposisi (superposition). Defleksi/lendutan sebagai akibat dari gaya geser pengaruhnya relative kecil, sehingga dalam perhitungan beberapa kondisi bisa diabaikan. Untuk melihat berapa besar lendutan yang terjadi, maka pada penugasan pembuatan rumah took dengan berlantai 2 dengan ukuran 6 x 9 m, dapat dihitung berapa defleksi pada balok sebagai akibat dari pembebanan.

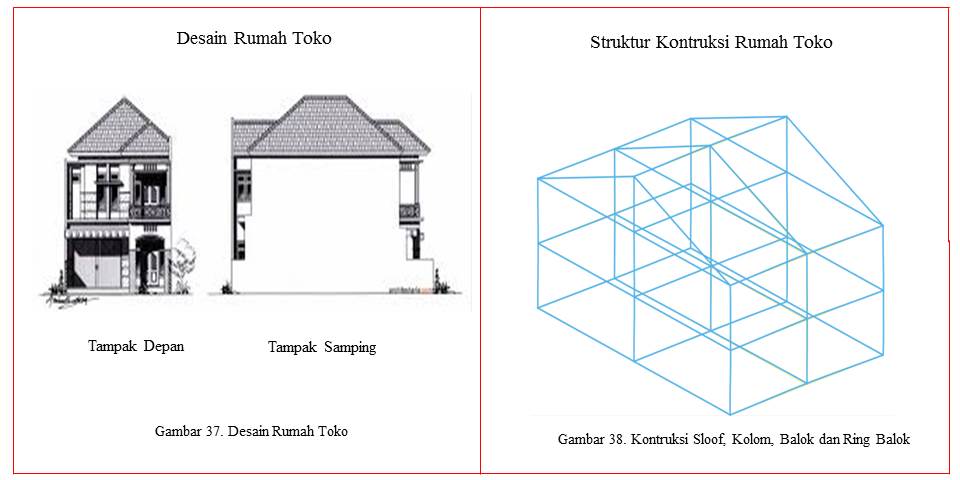
Bentuk rumah toko sesuai gambar 37 di atas, direncanakan dengan bentuk kolom dan balok dengan dimensi panjang 4,5m dan tinggi 3,5m, seperti terlihat pada gambar 38. Dengan kondisi demikian akan dapat dianalisa besarnya defleksi yang akan diterima oleh balok apabila mendapatkan beban dari luar. Dalam penghitungan akan dianalisis dengan menggunakan ketiga metode di atas.

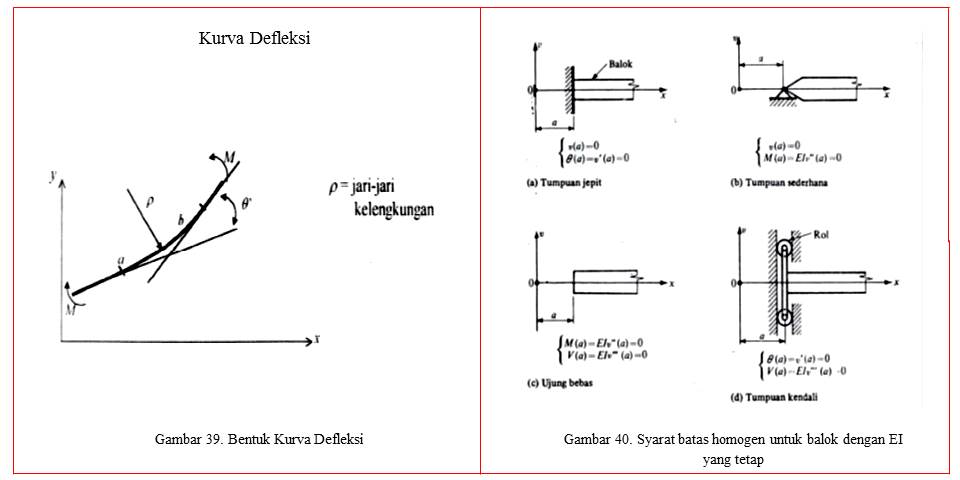
Tinjauan Pustaka Pada balok yang mendapatkan beban dari luar dapat diasumsikan seperti gambar 39 sebagai berikut:

Pada Gambar 39. diperlihatkan kurva defleksi batang yang menerima momen lentur. Hubungan antara kelengkungan dan momen lentur murni telah diperoleh. yaitu:

1/ρ=M/EI (1)

Sedangkan rumusan eksak untuk kelengkungan adalah

1/ρ=((d^2 y)/〖dx〗^2 )/[1+(dy/dx)^2 ]^(3/2)

1/ρ=(d^2 y)/〖dx〗^2 (2)

dy/dx merupakan slope kurva pada setiap titik.

Dimana

ρ : Jari-jari kelengkungan

M : Momen Lentur

E : Modulus Elastisitas

I : Momen Inersia

y : Jarak vertikal lendutan

x : Jarak sepanjang balok

Dari persamaan (1) dan (2) untuk defleksi yang kecil dapat dituliskan:

(d^2 y)/〖dx〗^2   =M/EI  

Momen lentur dari setiap segmen balok diantara titik-titik pembebanan dimana terjadi perubahan pembebanan, kemudian masing-masing akan diintegralkan untuk setiap segmen balok. Untuk menghitung konstanta integrasi dibutuhkan berbagai syarat batas dan kondisi kontinuitas. Syarat batas homogen untuk balok dengan EI yang tetap, diperlihatkan pada Gambar 41 dan gambar 42, sebagai berikut:

Pembahasan

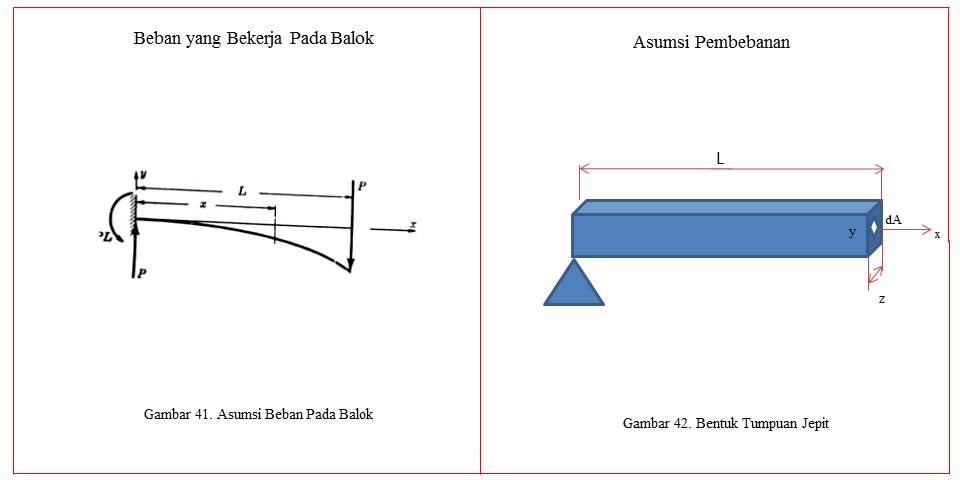
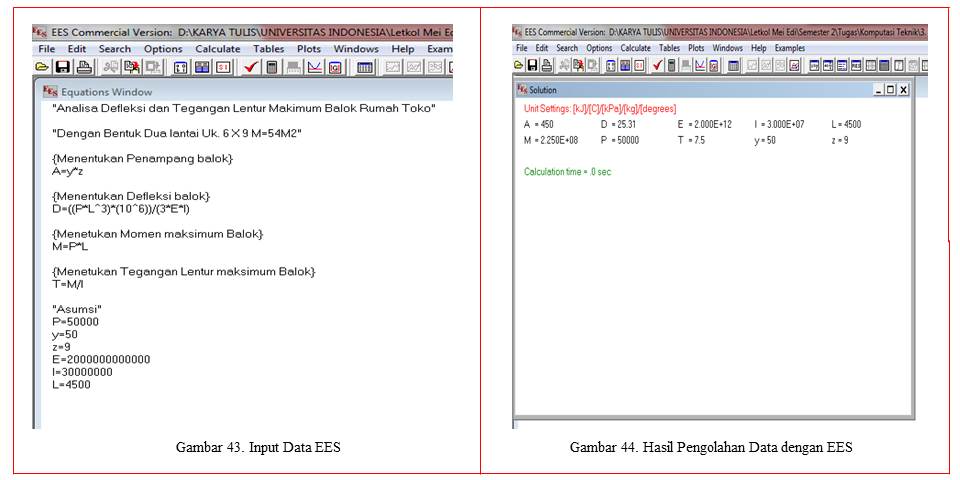
Dengan melihat perhitungan kekuatan balok rumah toko seperti gambar 45 dan gambar 46. Dengan asumsi bahwa panjang balok adalah 4,5m dengan beban 50kN, dimensi balok adalah 90x50 mm, memiliki Momen Inersia 300 x 106 mm4 dan modulus elastisitas 2000 GN/m2, dengan menggunakan program EES dapat dihitung besarnya defleksi maksimum dan tegangan lentur pada balok sebagai berikut:

Dari bentuk kontruski diatas dapat disusun besarnya defleksi balok sebagai berikut:

M= -PL + Px

EI (d^2 y)/〖dx〗^2 = -PL + Px (a)

Integrasi 1.

EI dy/dx= -PLx +〖Px〗^2/2 + C1 (b)

Integrasi 2.

EIy= -〖PLx〗^2/2 + 〖Px〗^3/6 + C1+ C2 (c)

Dari persamaan (c)

x = 0, y = 0, maka C2 = 0

Dari persamaan (b) x = 0, dy/dx = 0, maka C1=0

sehingga, EI dy/dx= -PLx +(Px^2)/2

Persamaan Defleksi EIy= -(PLx^2)/2 + (PL^3)/6 y maks pada saat x=L, maka  EIy= -(PL^3)/2 + (PL^3)/6 y maks= -(PL^3)/(3EI)

Untuk menghitung besarnya Nilai Defleksi dan Tegangan Lentur dapat dihitung dengan EES sebagai berikut:

Dari hasil perhitungan dengan menggunakan EES diketahui bahwa: Defleksi = 25,31 mm; Momen : 2,25 x 108; Tegangan: 7,5 Mpa

Kesimpulan

Dari hasil penghitungan dapat disimpulkan;

a. Struktur bangunan rumah toko dengan dimensi balok ukuran 50 x9 mm, Modulus elastisitas 200 x 1010N, beban 50kN mampu ditahan dengan defleksi sebesar 25,31mm.

b. Besarnya tegangan yang ditimbulkan sebesar 7,5 Mpa pada lengan terjauh pada L=4500mm.

Momen Inersia Dan Tegangan Normal Yang Bekerja Pada Penampang Balok

Pendahuluan

Pada sebuah kontruksi rumah toko, seperti pada penugasan besar sebuah balok melentur yang diakibatkan oleh bekerjnya beban-beban secara transversal terhadap sumbu pemanjangannya (x). Beban-beban ini menciptakan aksi internal, atau resultan tegangan dalam bentuk tegangan normal, tegangan geser dan momen lentur. Beban samping (lateral loads) yang bekerja pada sebuah balok menyebabkan balok melengkung atau melentur, sehingga dengan demikian mendeformasikan sumbu balok menjadi suatu garis lengkung. Kontruksi sebuah balok bangunan dapat disusun dengan berbagai penampang, baik mentuk profil H, I, Kotak, dll. Dalam perancangan kontruksi balok, tegangan yang terjadi, sifat penampang dan beban-beban luar dapat diperhitungkan Dengan demikian dengan kondisi penampang balok rumah toko yang dibuat dengan suatu model yang dapat dihitung, maka dapat diketahui besarnya momen inersia penampang, momen lentur pada penampang dan tegangan maksimum.

Tujuan

Tujuan pembelajaran dari momen inersia dan tegangan normal yang bekerja pada penampang balok adalah: a. Untuk memahami bagaimana konsep berfikir untuk mengidentifikasi beban yang bekerja pada penampang balok. b. Untuk menghitung bagaimana gaya yang bekerja, besarnya momen inersia dan besarnya tegangan maksimum. c. Untuk menganalisis beban yang bekerja pada balok secara keseluruhan baik momen inersia, tegangan lentur dan besarnya defleksi balok.

Tahapan Pemodelan

Dalam menyelesaikan permasalahan berapa nilai beban yang harus ditahan oleh sebuah balok rumah toko, diperlukan asumsi berapa besar beban-beban yang bekerja pada sebuah balok. Untuk memudahkan cara analisis diperlukan kerangka berfikir secara baik, sehingga dapat memahami permasalahan secara tepat dengan metode komputasi teknik. Adapun kerangka pemikiran dapat dilihat pada gambar 45 sebagai berikut:

Tegangan Lentur pada Balok.

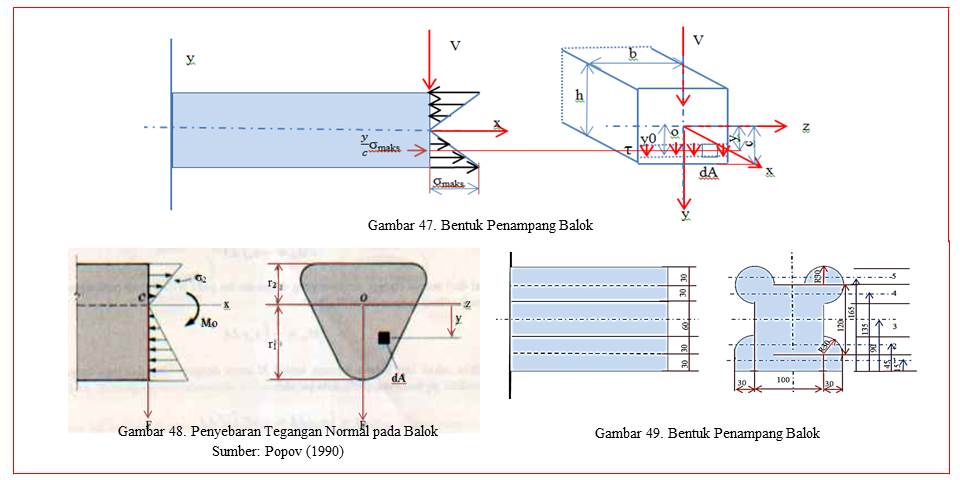
Menurut Popov (1990) apabila sebuah balok mendapatkan beban dan menyebabkan defleksi yang tidak merata, maka momen lentur M dan gaya lintang V kedua-duanya bekerja pada penampang. Tegangan normal (σx) yang berhubungan dengan momen lentur diperoleh dari rumus defleksi. Kasus sederhana dari sebuah balok berpenampang empat persegi panjang yang lebarnya b dan tingginya h (Gambar 3), dapat dimisalkan bahwa tegangan geser (T) bekerja sejajar dengan gaya lintang V (yaitu, sejajar dengan bidang-bidang vertikal penampang). Dimisalkan juga bahwa distribusi tegangan geser sama rata sepanjang arah lebar balok. Kedua penjelasan ini akan memungkinkan untuk menentukan secara lengkap distribusi tegangan geser yang bekerja pada penampang.

Tinjauan Pustaka.

Momen Inersia

Untuk dapat menghitung momen lentur harus dapat dihitung berapa momen inersia (I) dari irisan penampang terhadap sumbu netral. Besarnya momen inersia ditentukan oleh integrasi dari y2 dA terhadap seluruh luas irisan penampang. Momen inersia untuk lenturan/defelksi dihitung terhadap sumbu netral daerah irisan penampang. Sumbu ini harus melalui titik berat daerah penampang irisan. Untuk menghitung besarnya momen inersia bidang kecil dengan luas dA pada penampang balok seperti gambar 46 terhadap sumbu z-z sebagai berikut:

Izz=∫_A▒〖(d+y)^2 〗 dA

Izz=d^2 ∫_A▒〖dA+2d∫_A▒〖y dA+〗〗 ∫_A▒〖y^2 dA〗

       Izz=∫_A▒〖(d+y)^2 〗 dA

Izz=〖Ad〗^2+2d∫_A▒y dA+I0

Karena sumbu darimana y diukur adalah melalui titik berat dari sebuah luas penampang luas, integral ydA atau ýdA adalah nol. Sehingga, I_zz=〖Ad〗^2+I0, Persamaan ini disebut sebagai teorema sumbu sejajar.

Tegangan Lentur pada Balok.

Menurut Popov (1990) apabila sebuah balok mendapatkan beban dan menyebabkan defleksi yang tidak merata, maka momen lentur M dan gaya lintang V kedua-duanya bekerja pada penampang. Tegangan normal (σx) yang berhubungan dengan momen lentur diperoleh dari rumus defleksi. Kasus sederhana dari sebuah balok berpenampang empat persegi panjang yang lebarnya b dan tingginya h (Gambar 47), dapat dimisalkan bahwa tegangan geser (t) bekerja sejajar dengan gaya lintang V (yaitu, sejajar dengan bidang-bidang vertikal penampang). Dimisalkan juga bahwa distribusi tegangan geser sama rata sepanjang arah lebar balok. Kedua penjelasan ini akan memungkinkan untuk menentukan secara lengkap distribusi tegangan geser yang bekerja pada penampang.

Tegangan geser pada semua balok dengan jarak y dari sumbu netral diberikan dengan formula:

τ=V/Ib ∫_y^c▒ydA

Dimana: τ : tegangan geser b : lebar penampang balok y dA : momen area pertama V : gaya geser I : momen inersia

Suatu tegangan bekerja dalam arah normal terhadap penampang sebuah balok dari regangan normal ϵx. Tiap serat longitudinal dari sebuah balok hanya dikenakan beban tarik dan tekan (yaitu, serat-serat dalam tegangan uniaksial). Sehingga diagram tegangan-regangan bahan akan memberikan hubungan sebanding antara (σx) dan (ϵx). Jika bahannya elastis dengan suatu diagram tegangan-regangan linier, maka dapat digunakan Hukum Hooke untuk tegangan uniaksial (σ = Ee) dan diperoleh :

σx = Eϵx = Eky

Jadi, tegangan lentur yang bekerja pada penampang berubah secara linier terhadap jarak y dari permukaan netral. Jenis distribusi tegangan ini digambarkan pada Gambar 4, yaitu tegangan relatif (tekan) di bawah permukaan netral apabila kopel Mo bekerja dalam arah yang ditunjukkan. Kopel ini menghasilkan suatu kelengkungan positif K dalam balok, meskipun menyatakan suatu momen lentur negatif M

Tegangan normal pada suatu balok digambarkan oleh persamaan berikut: σ=Mc/I dimana σ : tegangan lentur M : momen lentur pada penampang y : jarak dari sumbu netral ke tegangan normal I : momen inersia

Pada penampang terluar balok nilai koordinat y dinotasikan dengan simbol c, sehingga tegangan normal maksimumnya menjadi:

σ maks=Mc/I atau

σ maks=Mc/(I/c)

I/c disebut modulus penampang yang umumnya dinotasikan dengan simbol Z. Sehingga tegangan lentur maksimum digambarkan oleh persamaan:

σ maks=Mc/Z

Defleksi

Sumbu sebuah balok akan berdefleksi (atau melentur) dari kedudukannya semula apabila berada di bawah pengaruh gaya terpakai. Defleksi Balok adalah lendutan balok dari posisi awal tanpa pembebanan. Defleksi (Lendutan) diukur dari permukaan netral awal ke permukaan netral setelah balok mengalami deformasi. Karena balok biasanya horizontal, maka defleksi merupakan penyimpangan vertikal. Persamaan Defleksi

EIy= -〖PLx〗^2/2 + 〖Px〗^3/6

y maks pada saat x=L, maka ==> EIy= -〖PL〗^3/2 +〖PL〗^3/6

y maks= -〖PL〗^3/3EI

Pembahasan

Terkait dengan tinjauan pustaka dihadapkan pada bentuk penampang balok rumah toko terbuat dari baja dengan modulus elastisitas 200x103 MPa, direncanakan dengan bentuk seperti gambar 5, dengan panjang 4.500mm, mendapatkan beban/gaya 45 kN pada bagian ujung, dianggap dengan satu tumpuan jepit. Dengan demikian dapat dihitung, momen inersia, tegangan maksimum, momen lentur dan defleksi sebagai berikut:

a. Momen Inersia

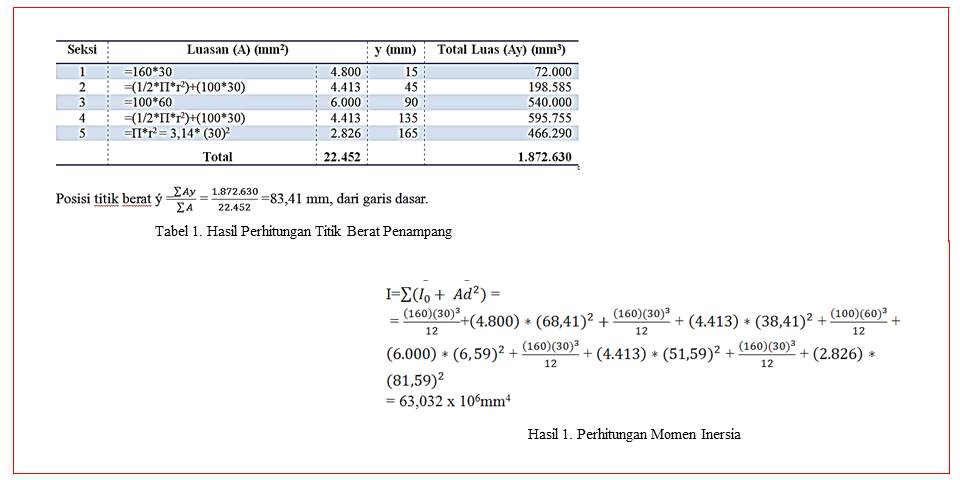
Untuk menghitung nilai momen inersia total digunakan pendekatan secara manual dan dengan pendekatan software EES. Secara manual untuk menghitung momen inersia penampang dapat diuraikan dari penjelasan dari tabel sebagai berikut:

Posisi titik berat ý =(∑▒Ay)/(∑▒A)

= 1.872.630/22.452

= 83,41 mm, dari garis dasar.

Untuk menghitung nilai momen inersia adalah

I=∑▒〖(I_0 〗+ 〖Ad〗^2) =

= ((160) 〖(30)〗^3)/12+〖(4.800)*(68,41)〗^2+((160) 〖(30)〗^3)/12 + 〖(4.413)*(38,41)〗^2 + ((100) 〖(60)〗^3)/12 + 〖(6.000)*(6,59)〗^2  + ((160) 〖(30)〗^3)/12 + 〖(4.413)*(51,59)〗^2 + ((160) 〖(30)〗^3)/12 + 〖(2.826)*(81,59)〗^2

= 63,032 x 106mm4

b. Tegangan Maksimum

Untuk menghitung besarnya tegangan maksimum di bagian atas penampang maupun bagian bawah penampang dapat disusun dengan rumus sebagai berikut:

σ maks=Mc/I = (45*4.500*96,59)/(63,032 x 〖10〗^6 ) = 0,3101 kN/mm2 =310,3 Mpa, pada permukaan atas (Tekan)

σ maks=Mc/I = (45*4.500*83,41)/(63,032 x 〖10〗^6 ) = 0,2680 kN/mm2 =268,0 Mpa, pada permukaan bawah (Tarik)

C. Defleksi

Untuk menghitung besarnya defelksi maksimum yang terjadi pada balok dapat ditentukan sebagai berikut:

y maks = -〖PL〗^3/3EI

  = -〖45.000*(4.500)〗^3/(3*200*〖10〗^3*63,032 x 〖10〗^6 ) 

  = 108,4 mm 

Menghitung dengan Software EES

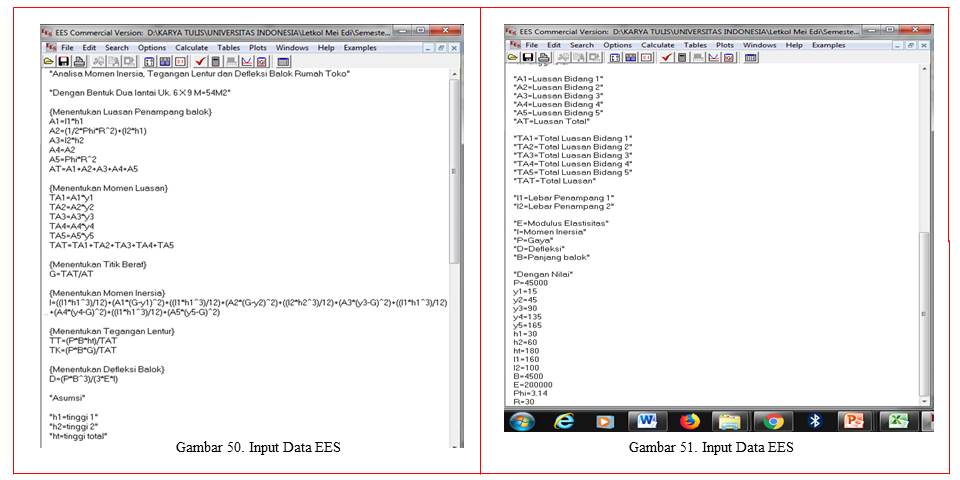
Dari hasi perhitungan secara manual, dicoba dengan menghitung dengan menggunakan program EES, didapatkan inputan data sebagai berikut:

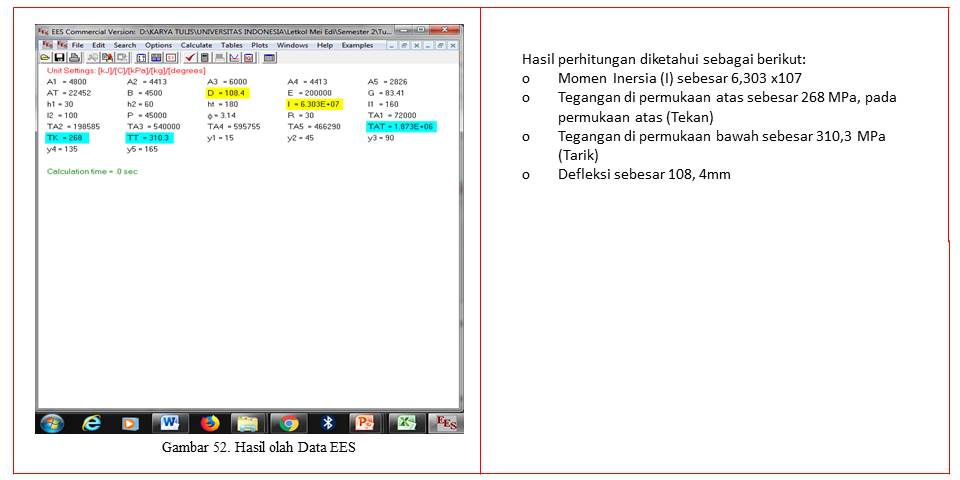
Hasil Pengolahan Data dengan EES

Dari hasil inputan data dengan menggunakan software EES didapat hasil sebagai berikut:

Kesimpulan

Dari hasil penghitungan dapat disimpulkan;

a. Untuk menghitung momen inersia suatu penampang yang tidak tentu diperlukan penghitungan tiap seksi.

b. Dari hasil perhitungan manual untuk mendapatkan nilai momen inersia, tegangan maksimal dan defleksi dibadingkan dengan hasil penghitungan dengan program EES didapat hasil yang relatif sama.