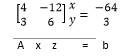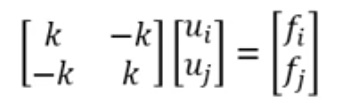Difference between revisions of "Muhammad Bagja Ramadhan"
| Line 229: | Line 229: | ||
[[File:fcuts.jpg]] | [[File:fcuts.jpg]] | ||
[[File:program computer.jpg]] | [[File:program computer.jpg]] | ||
| + | |||
| + | |||
| + | == UAS METNUM == | ||
| + | |||
| + | [[File:Poiu.jpg]] | ||
| + | |||
| + | [[File:uiop.jpg]] | ||
| + | |||
| + | [[File:tyuio.jpg]] | ||
| + | |||
| + | Berikut lampiran link video UAS : https://youtu.be/-HMzPspJKQw | ||
Revision as of 07:17, 29 May 2019
Contents
Review Materi Pertemuan 1 Metode Numerik
Kelas metode numerik pada pertemuan pertama dengar pengajarnya Bapak Dr. Ahmad Indra Siswantara dan Bapak Dr. Gunawan, kali ini membahas mengenai apa itu definisi dan tujuan dari kelas metode numerik itu sendiri. Tujuan Perkuliahan Metode Numerik adalah memahami konsep/prinsip dan mampu menerapkannya. kelas metode numerik ini pun merupakan lanjutan setelah seorang mahasiswa sudah mendapatkan kompetensi pelajaran kalkulus dan matematika teknik. Namun perbedaan dari kelas kalkulus dan matematika lainnya adalah metode numerik kita harus memprogramkan suatu perhitungan agar perhitungan tersebut dapat di hitung melalui komputer. Metode Numerik ini sendiri akan banyak mempelajari pemerograman dasar meliputi algoritma, flowchart, metode interative penyelesaian persamaan-persamaan aljabar simultan, diferensial dan integral, optimasi, serta studi kasus. Bapak Indra pun selaku dosen juga selain memberikan pemahaman tujuan dan konsep ilmu-ilmu Metode Numerik, beliau juga sendiri mengajari untuk menjadi orang yang lebih mengenal siapa dirinya. Pada dasarnya dalam dunia kerja atau pasca kampus sendiri pemerograman sendiri memiliki peran fundamental khususnya bidang engineering. Metode Numerik memiliki peran untuk mengoptimasi sebuah keadaan yang berhuungan dengan engineering sehingga mendapatkan output maksimum dengan input minimum perlu dibuat sebuah perhitungan matematis yang dapat mendefinisikan dan mencari solusi dari masalah yang ada contohnya sebagai berikut :
ΣF = 0 Dσ = 0
Contoh penurunan rumus diatas trsebut sendiri kita dapat mengetahui dan menentukan tegangan yang ada lalu kita dapat melakukan optimasi terbaik pengaturan tegangannya. Optimasi yang dilakukan menggunakan kecepatan perhitungan atau komputasinya yang dapat memberikan solusi terbaik dari berbagai keadaan dan percobaan yang ada dengan kurun waktu yang cepat dikarenakan menggunakan komputer yang lebih cepat daripada perhitungan manual. Dalam mempelajari Mata Kuliah ini tak semata-mata hanya mendapatkan bekal ilmu pengetahuan namu pula ilmu keagamaan dimana menurut Pak Indra Manusia diberkahi dengan akal Budi dari Tuhan Yang Maha Esa. Orang yang berakal dapat mengetahui yang mana yang benar yang mana yang salah, bijak berpikir dan bertindak. Dalam ilmu yang menggunakan matematis seperti Metode Numerik ini. Terkadang ilmu menjadi jawaban dan menyesatkan dimana banyak ilmuan ada yang meragukan adanya Tuhan karena ilmu pengetahuannya tersebut. Contoh yang dapat diambil menurut Pak Indra sebagai berikut.
lim┬(x→1)〖(x^2-1)/(x-1)〗
Dimana apabila kita langsung memasukan x=1 maka perhitungan yang didapat ialah tidak terdefinisi namun sebenarnya bukanlah tidak terdefinisi akan tetapi ilmu kita tidak sampai pada disana dan hanya Tuhanlah yang tahu. Pada dunia pasca kampus khususnya di prodi Teknik Perkapalan dalam menyelesaikan masalah menggunakan komputasi dilakukan pada kasus-kasus seperti Permasalahan membuat propeller yang tepat menggunakan OpenProp dan matlab sehingga propulsi yang dihasilkan seoptimal mungkin, dimana kita dapat menemukan ukuran dan bentuk propeller yang optimum menggunakan software matlab, lalu menggunakan juga CFD untuk mendapatkan aliran fluida yang ada pada propeller tersebut selain itu pulan dalam hal peletakan kamar mesin dan banyak sekali yang dapat diterapkan.
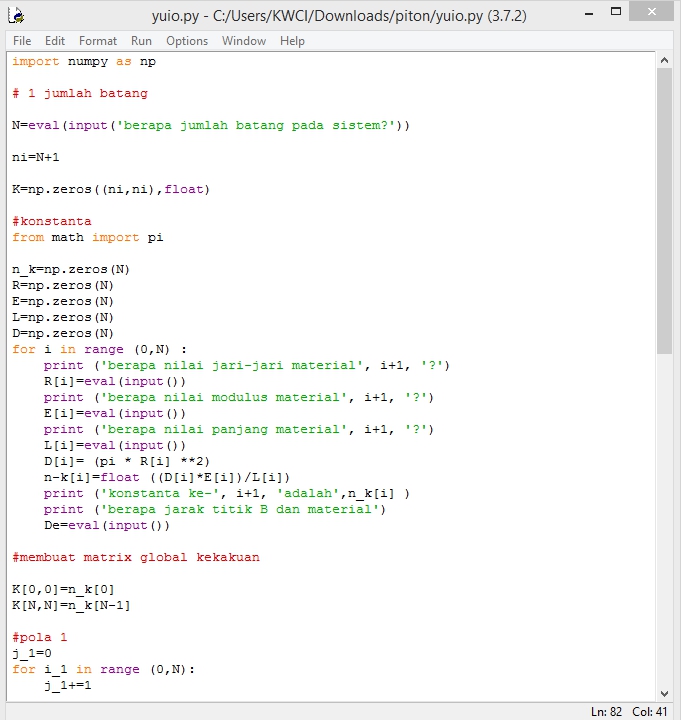
Perhitungan Algoritma menggunakan aplikasi Python
Pada kesempatan kali ini salah satu contoh atau tugas yang diberikan dalam memecahkan suatu masalah. Masalah tersebut di jabarkan kedalam suatu model matematis dan nantinya akan dihitung dengan ilmu metode numerik.
Selanjutnya metode numerik pun ini akan memecahkan dengan perhitungan algoritma, Dimana Algoritma sendiri merupakan langkah-langkah atau instruksi-intruksi komputasi dengan dijalankan dengan bahasa binary. Setelah dilakukan proses tersebut maka akan keluar hasilnya untuk di interpretasikan(solusi).
Dalam pertemuan kemarin, dalam menyelesaikan masalah, kami diwajibkan menggunakan aplikasi Python dimana aplikasi Python ini merupakan salah satu program memiliki fungsi seperti yang dijelaskan diatas.
untuk melakukannya maka penulis membuat contoh masalah yaitu:
4x-12y =-64
3x+ 6y =-3
setelah itu diubah menjadi bentuk matrix
kemudian dilakukan permisalan
setelah itu barulah kita menggunakan aplikasi python. Dalam hal ini diperlukan python numpy hal ini perlu dilakukan setelah menginstal python 3.7.2(aplikasi yang penulis gunakan) melalui CMD dengan memasukan command
setelah itu maka dilakukan step-step:
1. menambahkan module numpy: import numpy as np
2. memasukan perintah A=np.array([[4,-12],[3,6]])
3. memasukan perintah B=np.array([-64,3])
4. memasukan perintah z=np.linalg.solve(A,B)
5. memasukan perintah print(z)
6. didapatkan output yang diinginkan [-5.8 3.4]
flowchart :
contoh apabila berhasil memasukan perintah dengan benar
Metode Eliminasi Gauss
Metode eliminasi gauss merupakan metode penyelesaian persamaan linear dengan cara langsung. Maksud dari metode ini adalah membawa persamaan kedalam bentuk matrix, kemudian menyederhanakan matrix menjadi bentuk segitiga atas. Kemudian dilakukan subtitusi balik untuk mendapat nilai dari akar persamaan Setelah mendapat bentuk matrix tersebut. dalam pelajaran metode numerik ini kita akan menggunakan aplikasi python dengan menggunakan rumus dibawah ini, selain lebih cepat aplikasi ini dapat membantu apabila kita sudah mulai dihadapkan dengan perhitungan matrix yang banyak, berikut contohnya:
keterangan:
n = jumlah baris atau kolom
i = baris ke
j = kolom
k = pivot
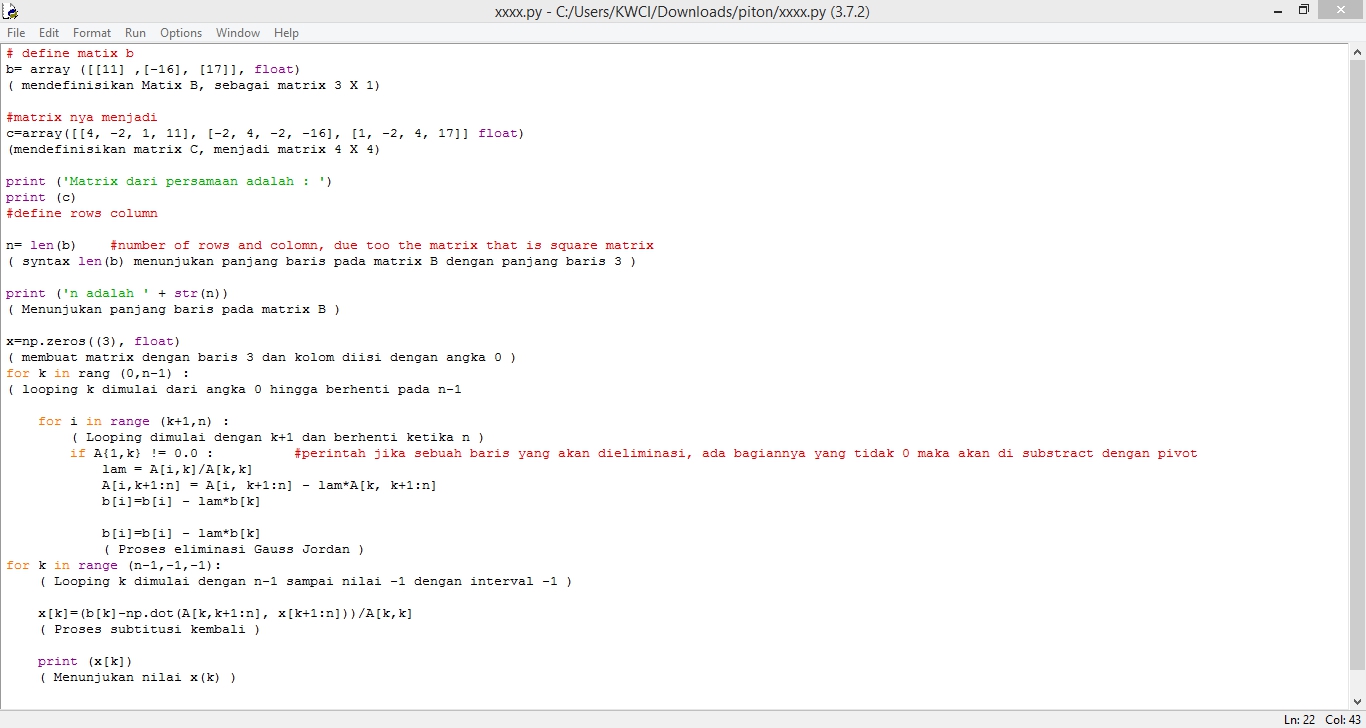
Langkah pengerjaan:
1. Memasukkan library numpy dengan cara memasukkan import numpy as np.
2. Memasukkan def gaussElimin(a,b): dimana def itu merupakan suatu fungsi, dan fungsi tersebut adalah eliminasi gauss dengan parameter a dan b. Baris berikutnya merupakan definisi dari n, di mana n tersebut adalah len(b) yang merupakan fungsi untuk mengembalikan angka atau objek berikut masuk ke fase eliminasi. hal yang pertama dimasukkan adalah fungsi range. Fungsi range ini berfungsi untuk menampilkan suatu list data, seperti yang dilihat untuk k range nya adalah (0,n-1)
3. Memasukkan fungsi range untuk i dimana fungsi tersebut parameternya adalah (k+1,n) dimana dapat ditranslate sesudah kita mengetahui nilai k yang ingin dimasukkan. Dilanjutkan dengan memasukkan fungsi if dimana, if yaitu bila suatu kondisi tertentu tercapai maka apa yang harus dilakukan. Dengan fungsi ini kita bisa menjalankan suatu perintah dalam kondisi tertentu. Dimana perintah tersebut disini adalah a[i,k ] !=0.0: . setelah itu dilanjutkan dengan perhitungan lam dan perhitungan lainnya
4. Melakukan fase substitusi balik, sehingga mendapatkan hasil sebagai berikut:
Contoh Latihan yang dilakukan
Pertemuan 4
pada kesempatan kali ini kami diajarkan menggunakan aplikasi python dimana banyak pengetahuan dan informasi-informasi sebagai berikut :
1. Numpy =merupakan direktori untuk python (sebelum menggunakan python maka wajib untuk mendownload numpy melalui Command Prompt/CMD dengan penulisan sebagai berikut) ==> pip instal numpy
2. dalam melakukan sesuatu maka diharuskan mengetik import numpy as np diman ini berfungsi untuk python dapat mengerti perintah yang ada menggunakan library numpy
3. A = np.array ==> perintah untuk membuat matrix dari librari (np)
4. '\n' = untuk membuat enter
5. # = notes milik user dan tidak dibaca oleh pyton
6. "k" = untuk dijadikan pivot baris pertama merupakan baris ke 0
7. ":" = untuk dijadikan penanda ada perintah didalamnya
8. perbedaan antara
import numpy as np = hanya diperlukan tambahan tulisan np didepannya
from numpy import array = harus mengetik ulang setiap kali ingin menambahkan sin/cos
tak hanya itu para mahasiswa pun melakukan latihan secara langsung berikut hasil dari latihan berikut :
TUGAS APLIKASI ALJABAR LINIER MELALUI PYTHON
Diketahui ada seorang pengusaha yang inginmembangun sebuah kos-kosan. Ia ingin membangun kos dengan 3 lantai yaitu dengan 3 macam kamar, kamar tanpa kamar mandi dalam, kamar dengan kamar mandi dalam dan kamar dengan kamar mandi dalam + AC.
Pada lantai pertama kamar tanpa kamar mandi dalam sebanyak 4 ruangan, kamar dengan kamar mandi dalam 2 ruangan dan kamar dengan kamar mandi dalam + AC sebanyak 3 ruangan. Sebulan pendapatan dari kamar tersebut sebesar Rp.130 juta.
Pada lantai kedua kamar tanpa kamar mandi dalam sebanyak 3 ruangan, kamar dengan kamar mandi dalam 3 ruangan dan kamar dengan kamar mandi dalam + AC sebanyak 2 ruangan. Sebulan pendapatan dari kamar tersebut sebesar Rp.115 juta.
Pada lantai ketiga kamar tanpa kamar mandi dalam sebanyak 2 ruangan, kamar dengan kamar mandi dalam 2 ruangan dan kamar dengan kamar mandi dalam + AC sebanyak 3 ruangan. Sebulan pendapatan dari kamar tersebut sebesar Rp.110 juta.
• Berapakah harga sewa dari masing masing perbulan kamar? • Anggap modal pembangunan sebesar 13.850.000.000 dengan biaya operasional sebesar RP.7.000.000 berapakah BEP nya
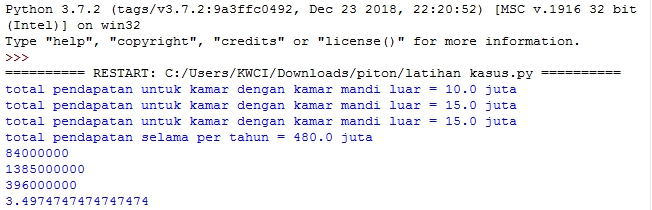
langkah langkah dapat dilakukan dengan mengetik perintah di file python ataupun langsung dari python shell tersebut
melalui file new python:
melalui shell pyton langsung:
untuk melihatnya lebih mudah dapat diakses melalui video di youtube
video youtube : https://youtu.be/-HMzPspJKQw
TUGAS PERTEMUAN 5
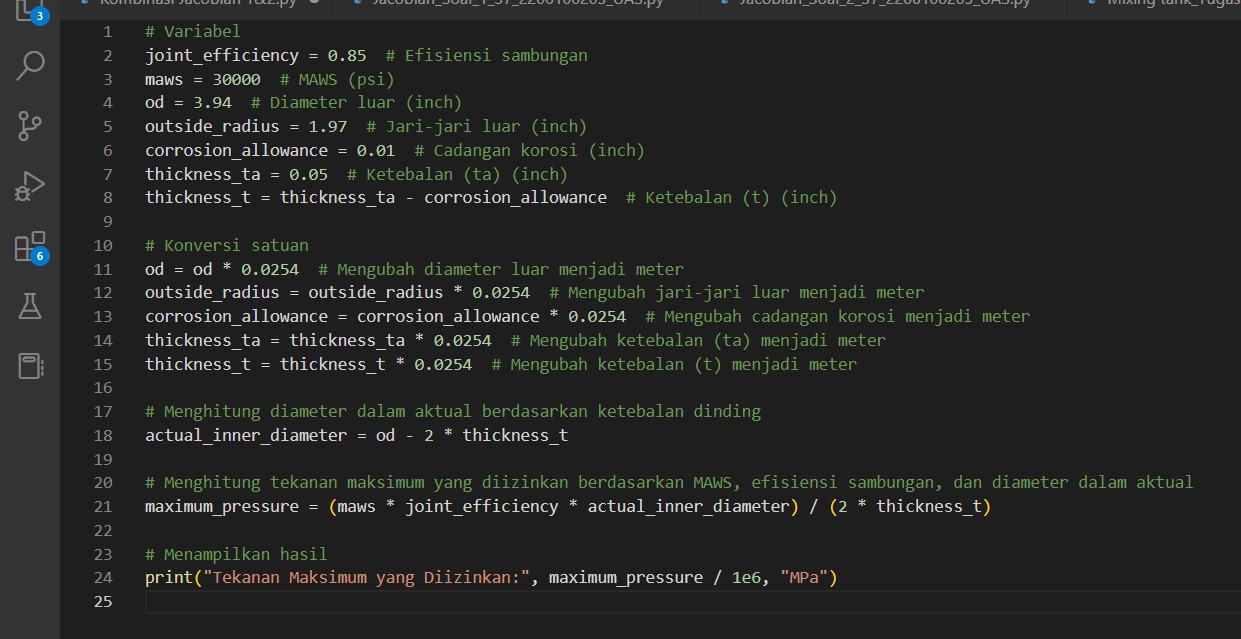
Digunakan perhitungan metode finite elemenet analysis (FEA) pegas untuk pengaplikasian perhitungan eliminasi gauss .Caranya mengubah bentuk persamaan untuk perhitungan gaya pegas ke dalam bentuk matrix untuk penghitungannya. Berikut adalah perhitungannya
untuk penghitungan satu buah pegas
dimana :
x = arah gaya
u = perpindahan/ displacement
f = gaya
k = konstanta pegas
i = titik i
j = titik j
dapat diketahui bahwa dalam satu pegas memiliki dua node yaitu pada masing masing ujung pegas. anggap kedua node tersebut sebagai i dan j. untuk menghitung suatu FEA pegas kita dapat menghitung dengan menggunakan F= k . delta. dimana k adalah koefisien pegas dan delta adalah pengurangan displacement antara masing masing node ialah sma dengan
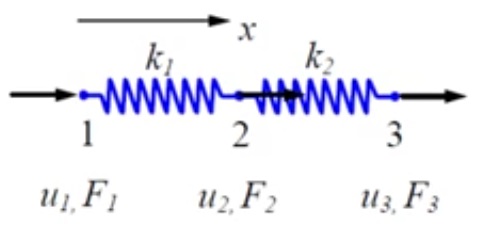
persamaan diubah kedalam bentuk matrix agar kita dapat menggunakan eliminasi gauss untuk enghitung FEA nya. hasil nya tersebut berupa gaya dari masing masing node
penghitungan itu juga dapat digunakan untuk menghitung pegas dalam bentuk rangkaian seri. contohnya anggap kita memiliki dua pegas yang dirangkai secara seri. dikarenakan pegas tersebut merupakan pegas seri, node yang dihasilkan sebanyak 3 buah, dimana menyebabkan terbentuknya matrix 3x3 pada saat perhitungan eliminasi gauss nya. selain itu juga displacementnya menjadi sebanyak 3 buah juga untuk masing masing node. sehingga dapat disimpulkan bahwa jumlah node sama dengan jumlah spring ditambah dengan satu
bentuk matrix berdasarkan persamaan nya
untuk penghitungannya terdapat beberapa tahap yaitu
1. menentukan matrix global stiffness
2. menentukan displacement pada node tetap adalah 0 atau tidak ada displacement sama sekali
3. menententukan displacement 1, 2, 3, ..., n dengan menggunakan eliminasi gauss
4. menententukan gaya reaktsi berdasarkan hasil yang di dapatkan
APLIKASI ELIMINASI GAUSS 2
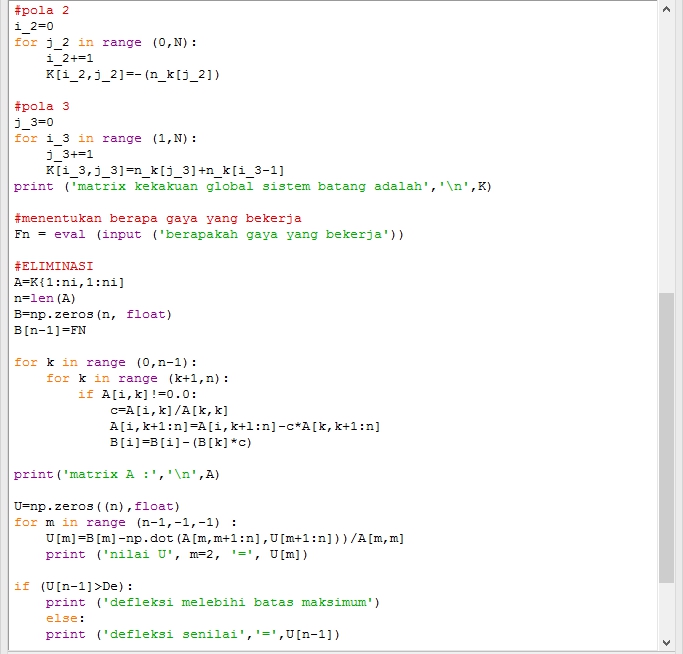
UTS Metnum
dalam kesempatan kali ini kami diberikan tugas untuk mengerjakan UTS mengenai struktur 3D
untuk lebih jelasnya dapat dilihat di gambar berikut
File:Fcuts.jpg File:Program computer.jpg
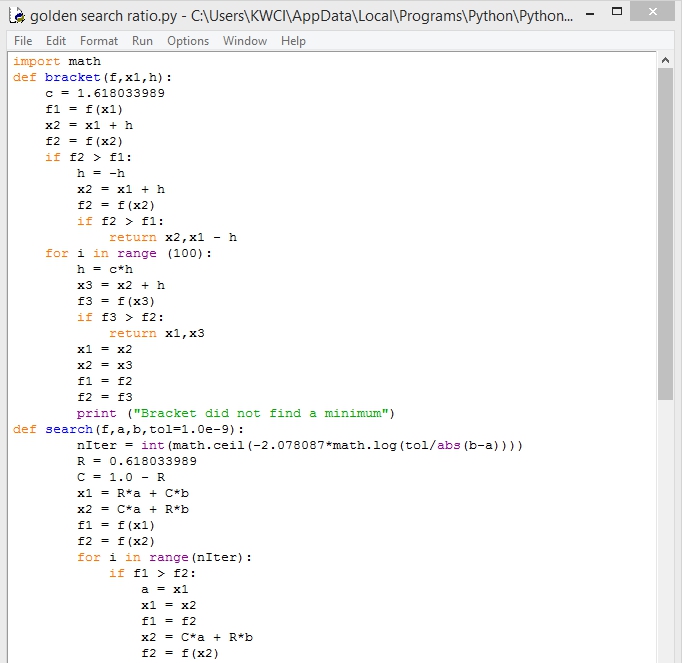
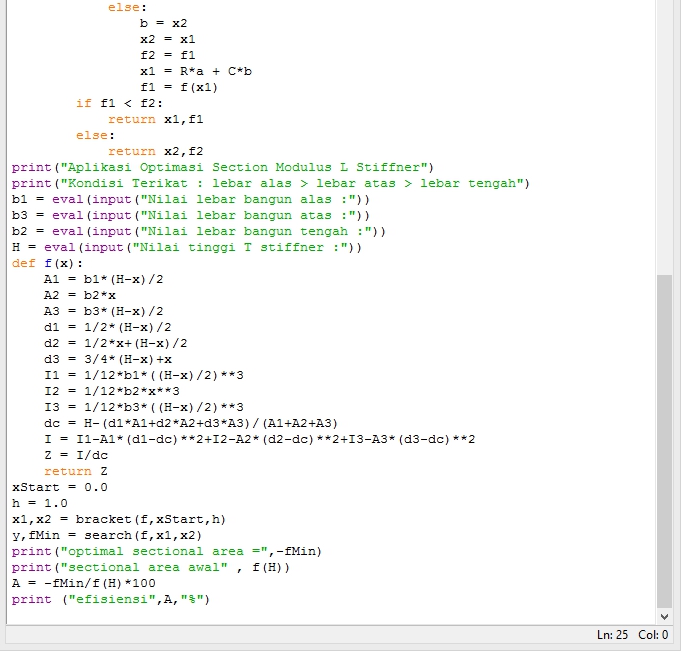
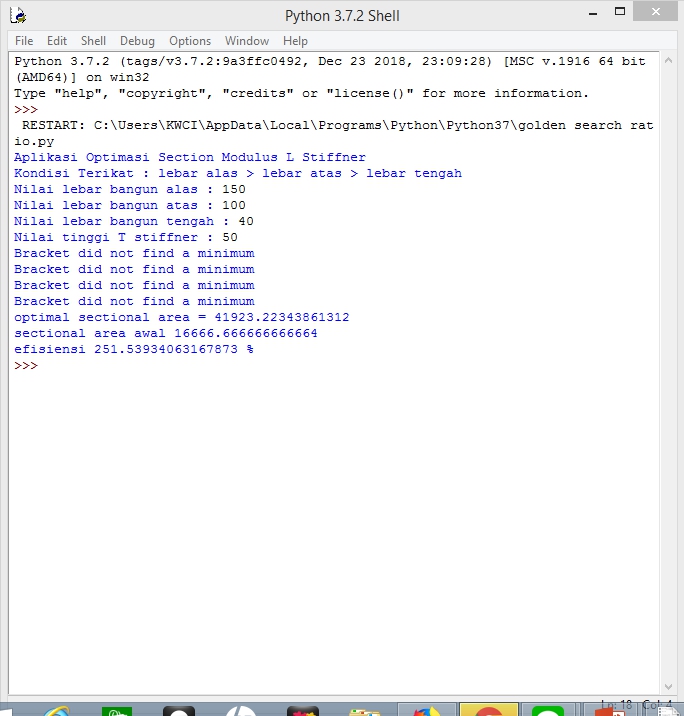
UAS METNUM
Berikut lampiran link video UAS : https://youtu.be/-HMzPspJKQw