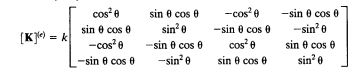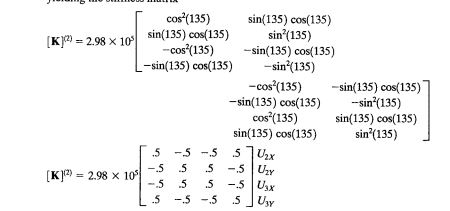Difference between revisions of "Metnum03-Gandes Satria Pratama"
Gandessatria (talk | contribs) m |
Gandessatria (talk | contribs) (→UAS (Ujian Akhir Semester)) |
||
| Line 809: | Line 809: | ||
=''' UAS (Ujian Akhir Semester)'''= | =''' UAS (Ujian Akhir Semester)'''= | ||
| + | |||
| + | Pada tanggal 13 januari 2021 diadakan UAS. Berikut Jawaban UAS. | ||
| + | |||
| + | Jawaban No.1 | ||
| + | |||
| + | [[File:UAS_GSP_001.jpg|500px|center]] | ||
| + | |||
| + | Jawaban Nomor 2 | ||
| + | |||
| + | [[File:UAS_GSP_002.jpg|500px|center]] | ||
| + | |||
| + | Jawaban Nomor 3 | ||
| + | |||
| + | [[File:UAS_GSP_003.jpg|500px|center]] | ||
| + | |||
| + | Jawaban Nomor 4,5,6 | ||
| + | |||
| + | [[File:UAS_GSP_004-007.jpg|500px|center]] | ||
| + | |||
| + | Codingan | ||
| + | --- | ||
| + | |||
| + | class UAS_Gandes | ||
| + | parameter Real [:,5] inisiasi = [1,1, 2, 40, 28.5e6, 480; | ||
| + | 1,1, 3, 40, 28.5e6, 480; | ||
| + | 1,1, 4, 40, 28.5e6, 480]; | ||
| + | |||
| + | |||
| + | parameter Integer [:,2] node = [1, 2; | ||
| + | 1, 3; | ||
| + | 1, 4]; | ||
| + | |||
| + | parameter Integer y = size(node,1); | ||
| + | |||
| + | parameter Integer x = 2*(size(node_load,1)); | ||
| + | |||
| + | parameter Integer z = size(Boundary,1); | ||
| + | |||
| + | parameter Integer [:] Boundary = {3}; | ||
| + | |||
| + | parameter Real [:,3] node_load = [1, 0, 2503621.3356 ; | ||
| + | 2, 0, 0; | ||
| + | 3, 0, 0]; | ||
| + | parameter Real [2*(size(node_load,1))] load = {0,2503621.3356,0,0,0,0,0,0}; | ||
| + | Real [y] k; | ||
| + | Real [y,4,4] Ke; | ||
| + | Real [y,x,x] Kg; | ||
| + | Real [x,x] KgTot; | ||
| + | Real [x,x] KgB; | ||
| + | Real [x] U; | ||
| + | Real [x] R; | ||
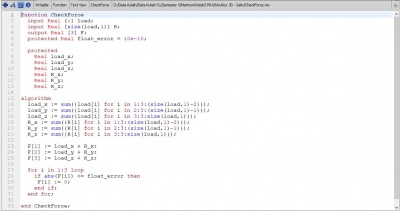
| + | equation | ||
| + | k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)}; | ||
| + | Ke = StiffnessMatrixElement(inisiasi); | ||
| + | Kg = StiffnessMatrixGlobal(node, x, y, Ke); | ||
| + | KgTot = SumStiffnessMatrixGlobal(x, y, Kg); | ||
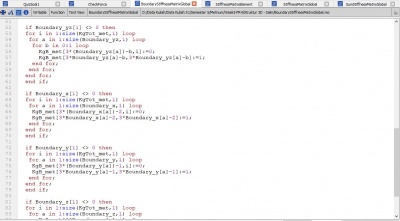
| + | KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary); | ||
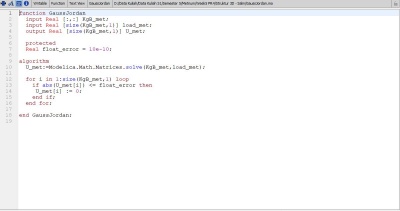
| + | U = GaussJordan(x, KgB, load); | ||
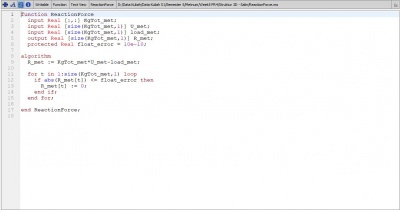
| + | R = ReactionForce(x, KgTot, U, load); | ||
| + | |||
| + | class UAS_Gandes | ||
Revision as of 22:46, 13 January 2021
Contents
- 1 BIODATA DIRI
- 2 Pertemuan 1 (9 November 2020)
- 3 Pertemuan 2 (16 November 2020)
- 4 Pertemuan 3 (23 November 2020)
- 5 Pertemuan 4 (30 November 2020)
- 6 Pertemuan 5 (7 Desember 2020)
- 7 Pertemuan 6 (14 Desember 2020)
- 8 Pertemuan 7 (21 Desember 2020)
- 9 Tugas Besar Metode Numerik
- 10 UAS (Ujian Akhir Semester)
BIODATA DIRI
Assallammualaiakum Warrahmatullahi Wabarakatuh.
Alhamdulillah, segala puji bagi Allah SWT Tuhan semesta alam dan sholawat beserta salam kepada Nabi Muhammad SAW.
Nama : Gandes Satria Pratama
NPM : 1906435492
Email : Gandessatria@gmail.com / Gandes.Satria@ui.ac.id
No. Handphone : 081220792803
Pertemuan 1 (9 November 2020)
Materi sebelum UTS
Materi yang diajarkan sebelum UTS adalah sebagai berikut
1. Deret Taylor dan Deret Mclaurin
2. Pencarian Akar - Akar
Pada Pencarian akar akar ini ada 2 metode yang digunakan, yaitu metode menggunakan Open Methods dan Bracketing Method. Pada open methods diajarkan menggunakan Newton Rhapson, Simple Fix Point dan Secant Method. Sedangkan pada metode bracketing diajarkan menggunakan False methods dan Bisections.
3. Penurunan Numeric Pada penurunan ini kita diajarkan penurunan secara backward, forward dan center.
4. Regresi Linear dan Interpolasi
5. Gauss-Jordan dan Aljabar
Tutorial Menggunakan OpenModelica
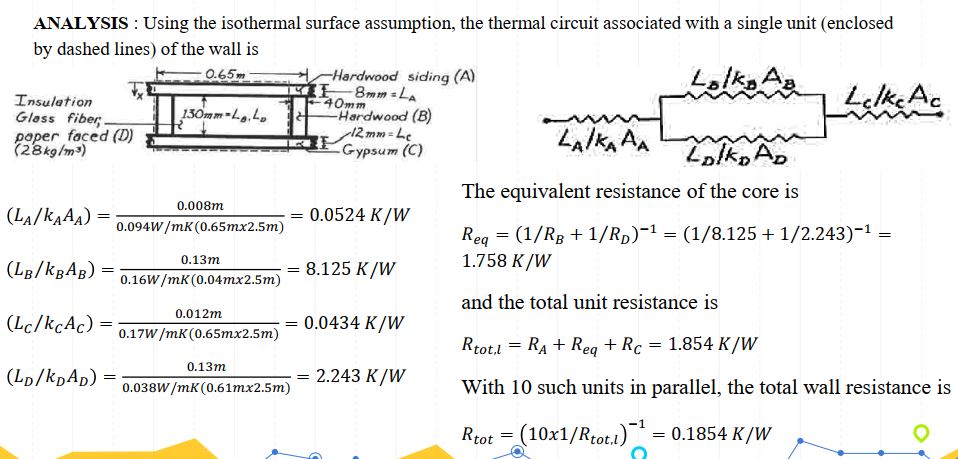
Pada pertemuan ini ditugaskan untuk mempelajari dan mengenal software OpenModelica. Pada tugas ini saya mencoba menggunakan open modelica dalam menyelesaikan soal thermal resistance. Berikut ini adalah soal dari thermal resistance beserta hasilnya.
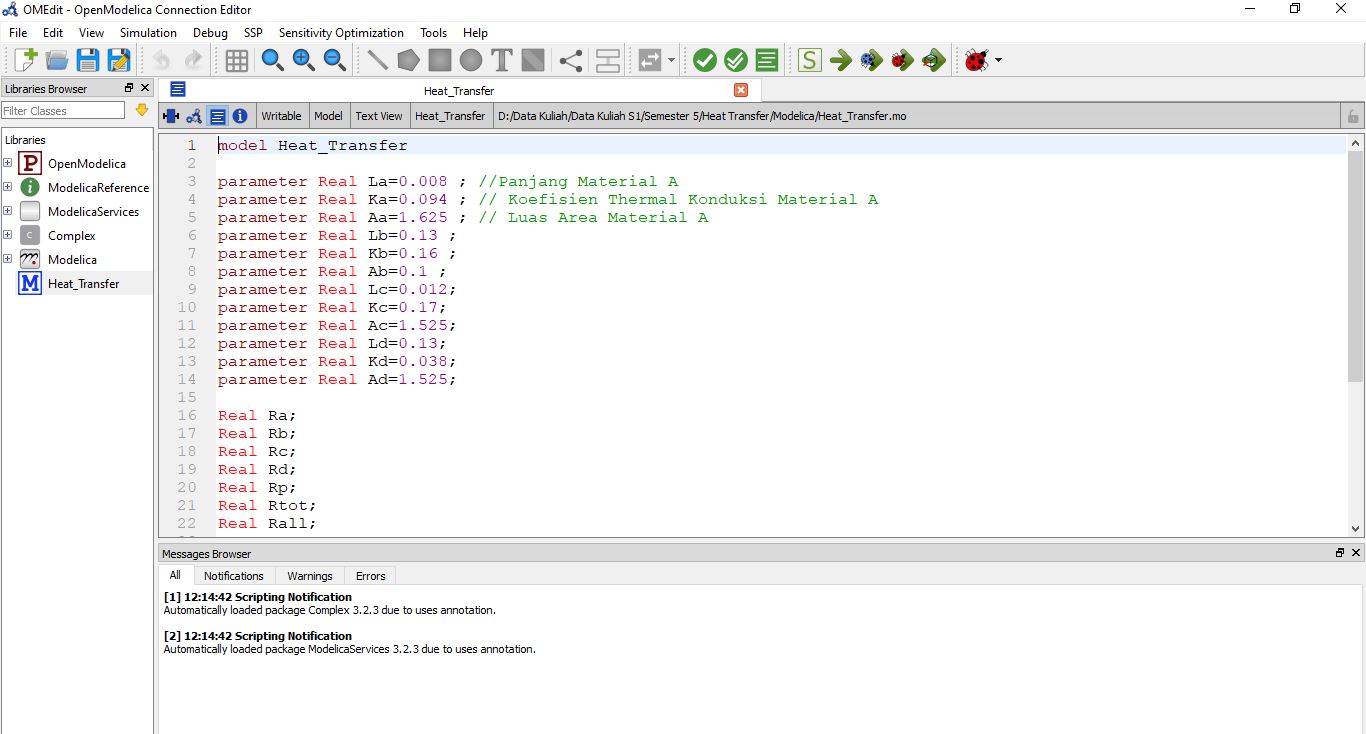
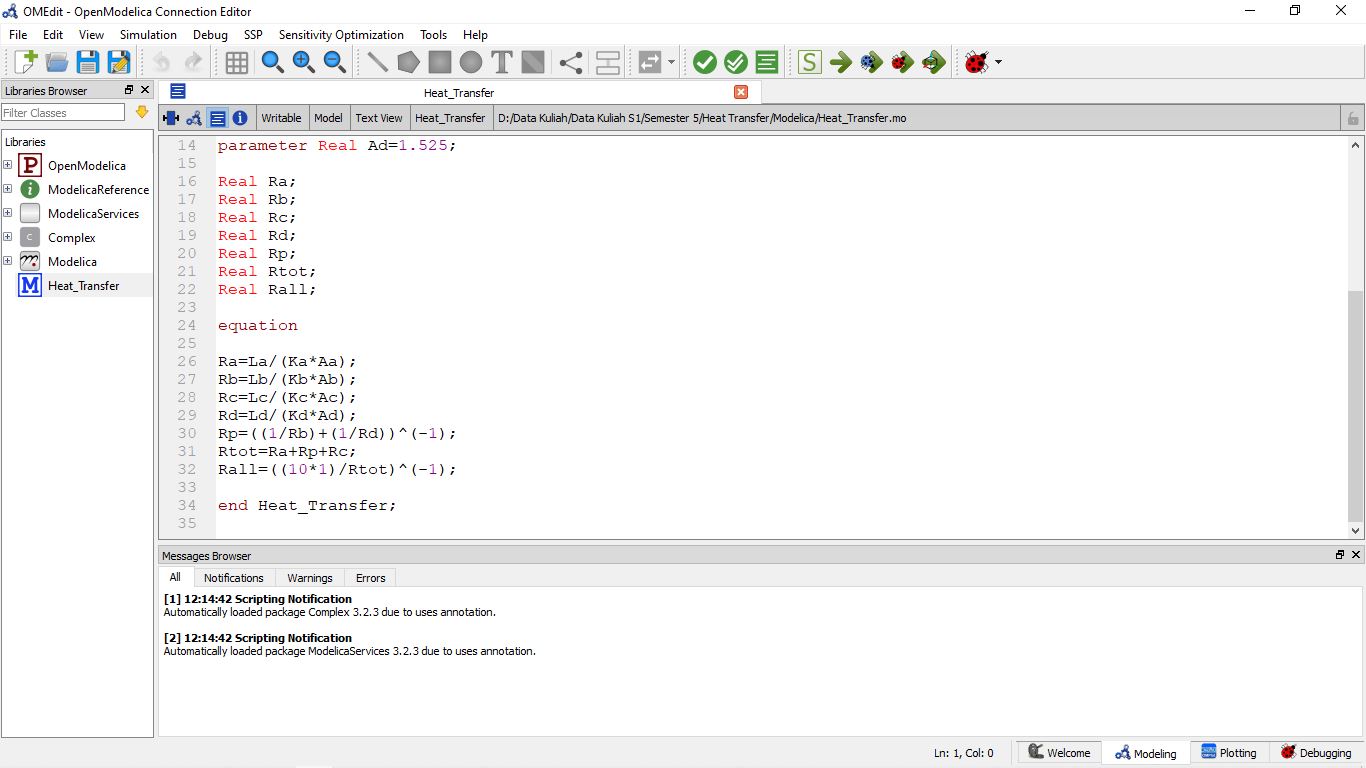
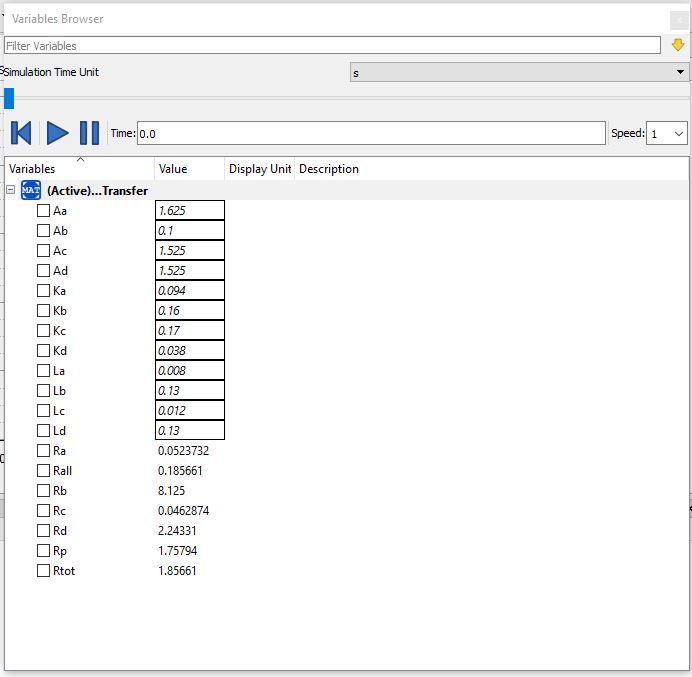
Dan berikut ini adalah coding openmodelica dan hasilnya.
Dan berikut link video tutorial dalam menggunakan openmodelica.
https://www.youtube.com/watch?v=0ECIS6ybP9w&t=7s
Pertemuan 2 (16 November 2020)
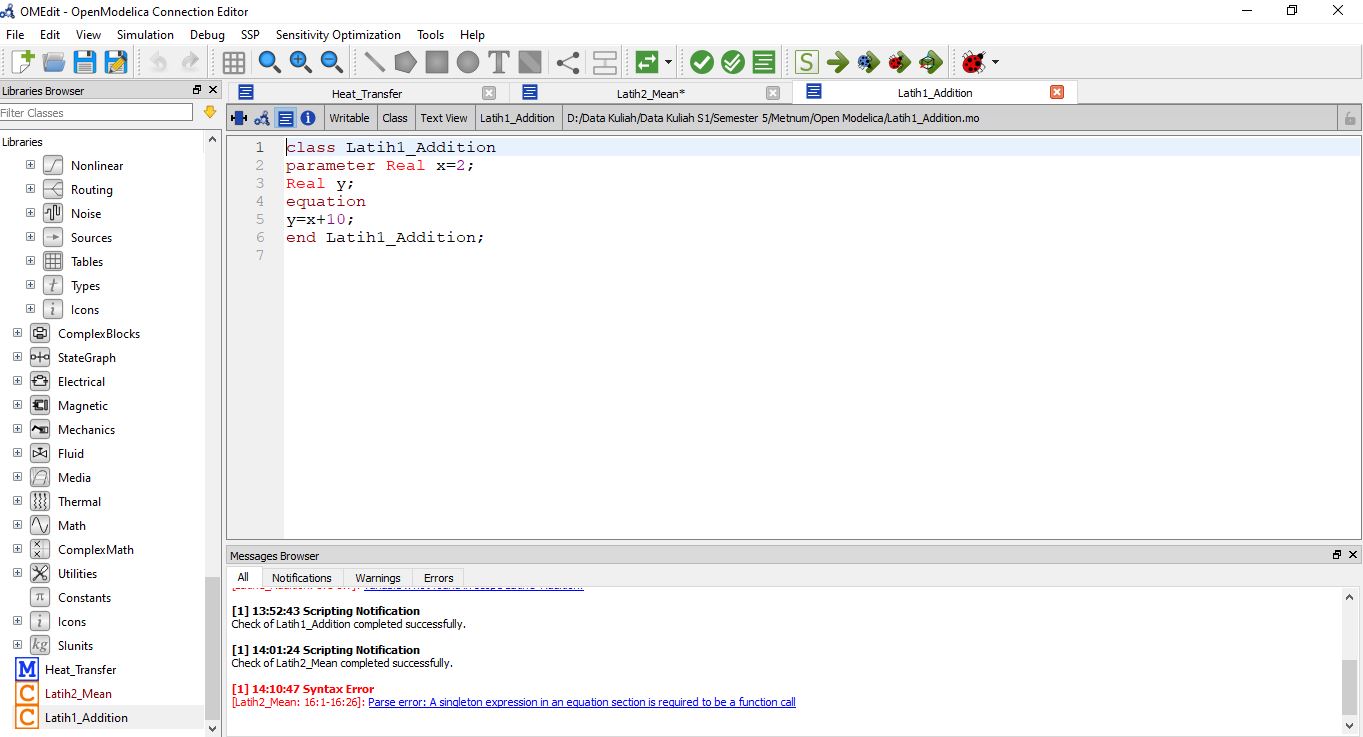
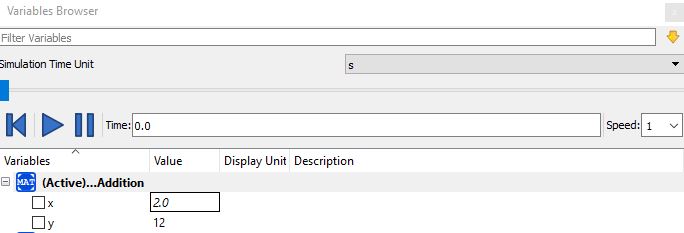
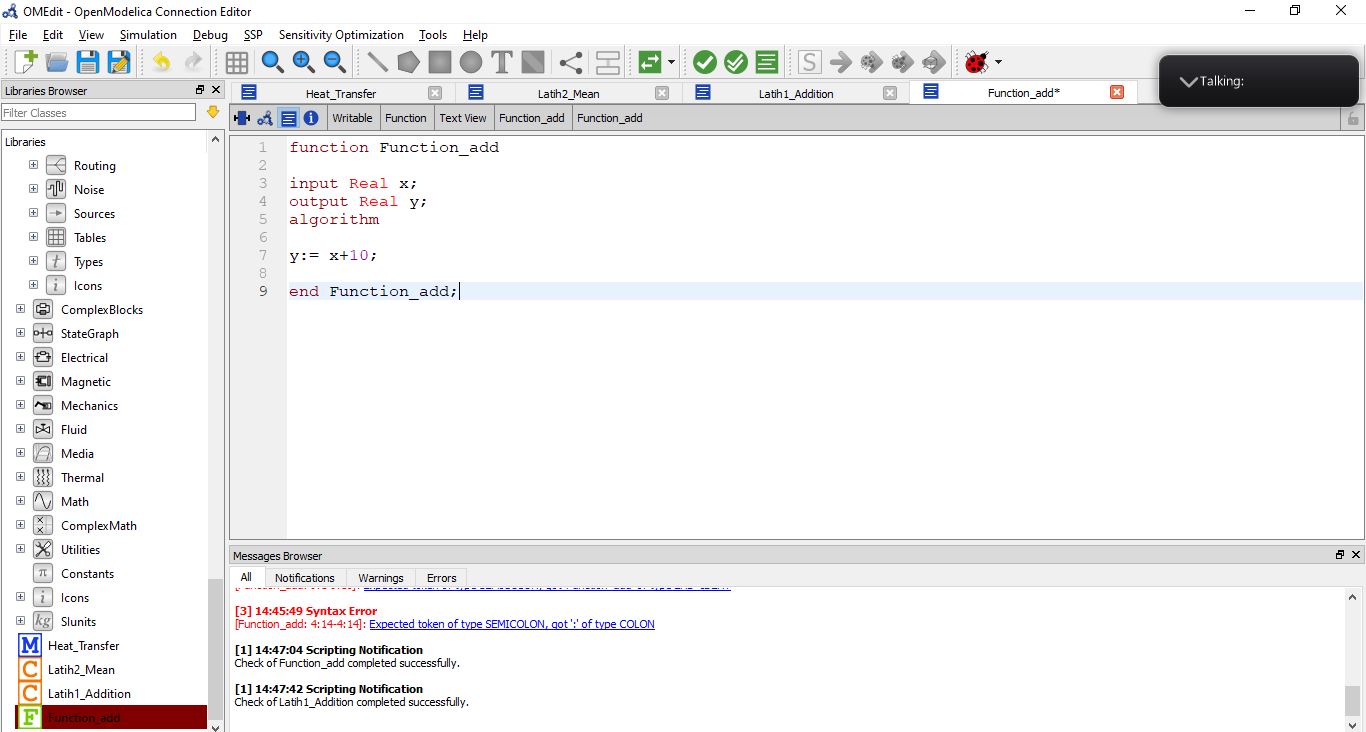
Latihan 1 dengan membuat program kecil dimana persamaannya y = x + 10 lalu di running dengan openmodelica. lalu mencoba dengan merubah x dan memastikan bahwa nilai sesuai.
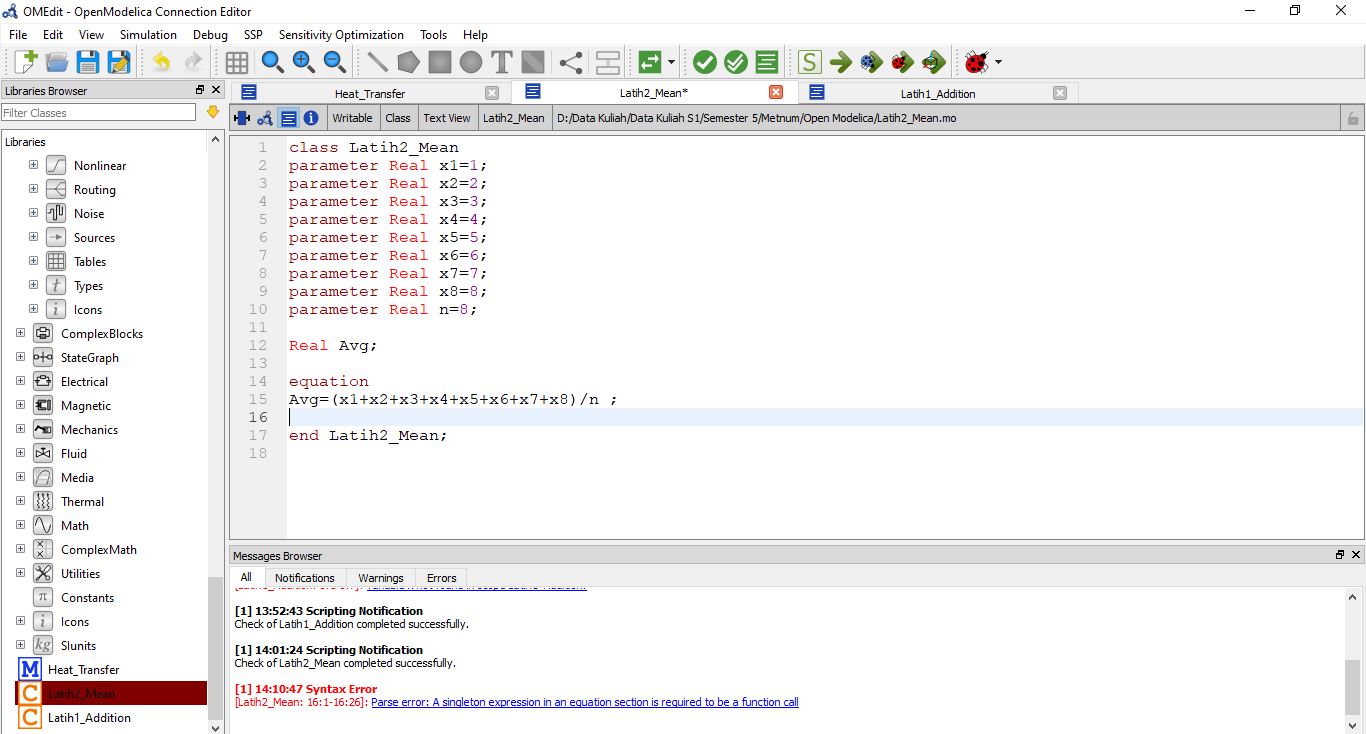
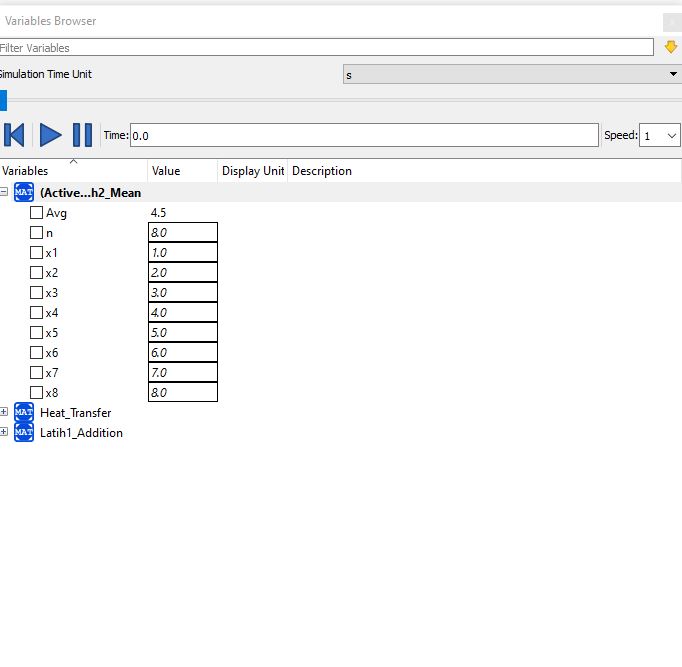
Lalu membuat latihan 2 bagaimana mencari mean. Berikut hasil open modelica yang saya lakukan.
Lalu kita mempelajari menggunakan function mode. Dimana function mode dapat digunakan pada equation pada class.
contoh coding pada function mode.
Function dimasukan kepada equation di class mode.
Hasil dari simulasi class mode.
Latihan Tugas Minggu 2
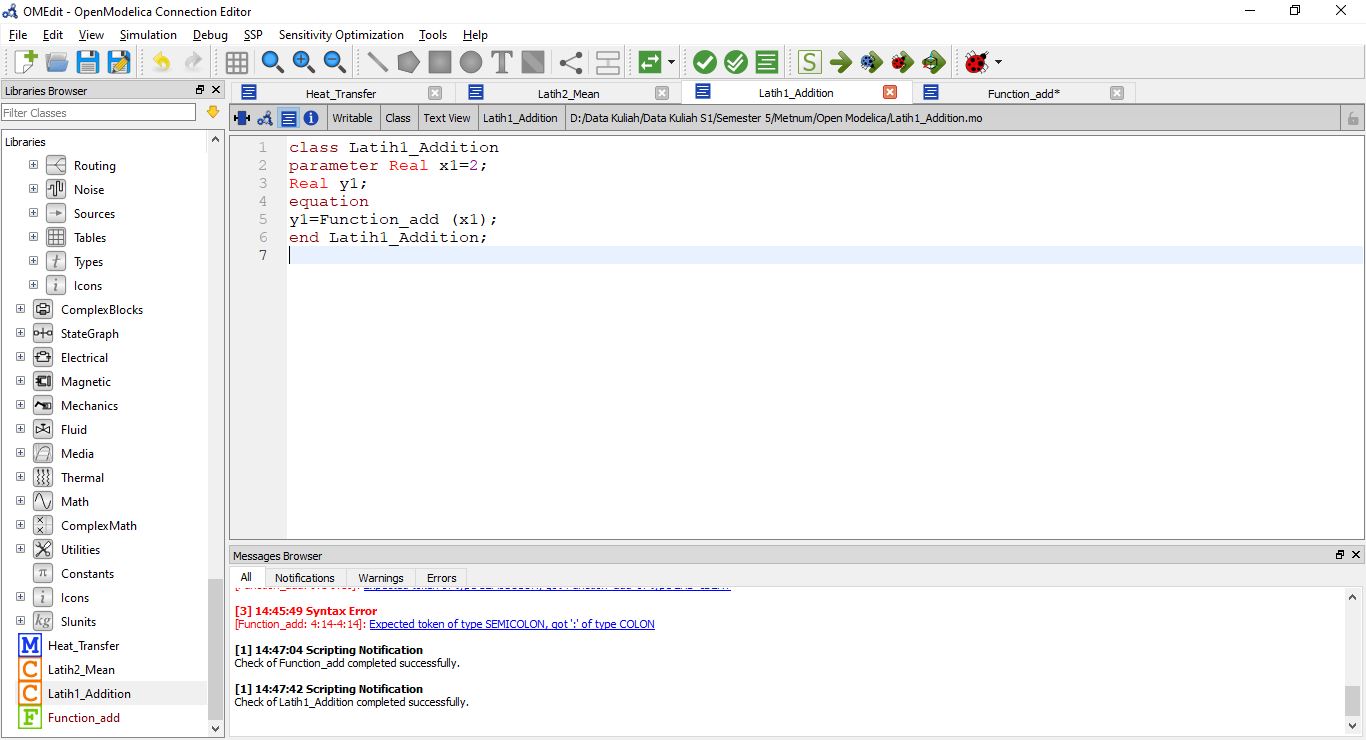
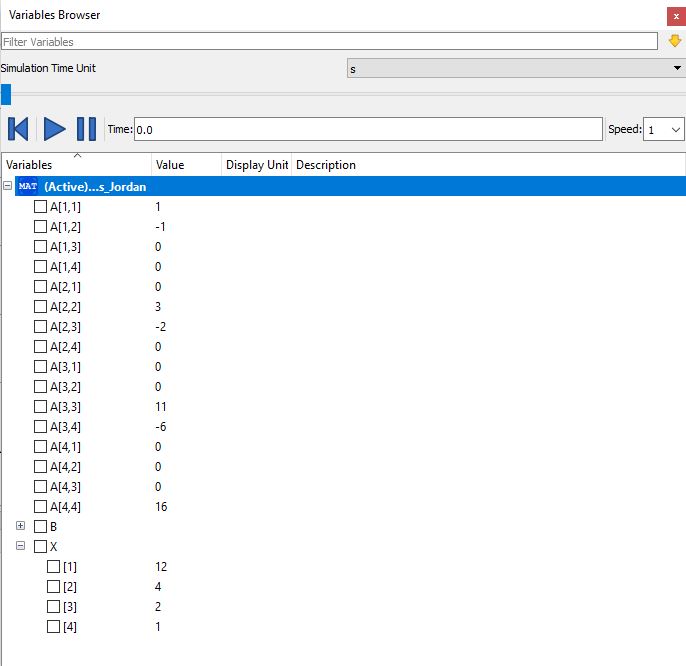
Pada minggu ini pak dai memberikan tugas untuk menyelesaikan aljabar menggunakan open modelica. Saya mencoba melakukan dengan persamaan sebagai berikut.
Lalu saya melakukan coding di modelica seperti berikut
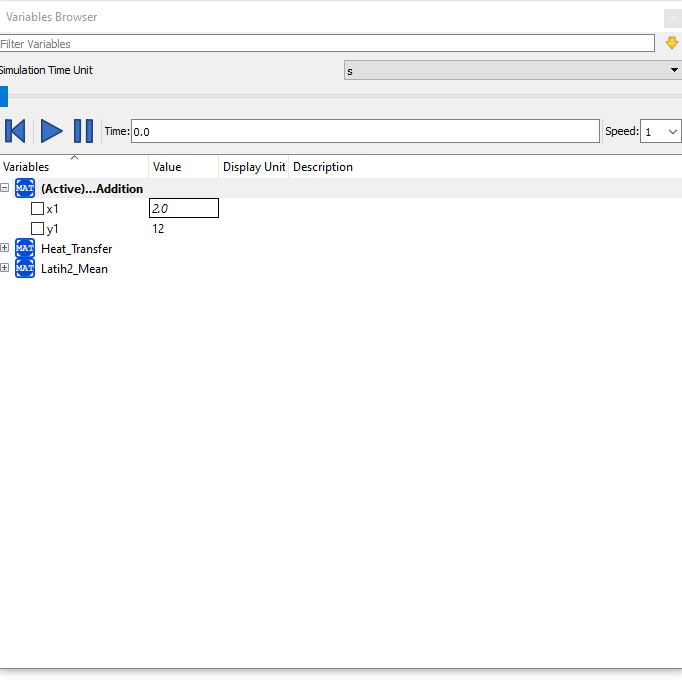
Lalu hasilnya menjadi seperti ini
Dapat dilihat hasil dari foto pertama dengan hasil foto diatas nilai x1, x2, x3, x4 sama dan sesuai.
Pertemuan 3 (23 November 2020)
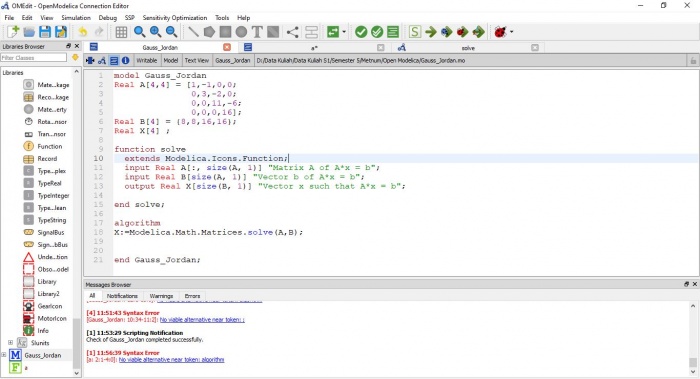
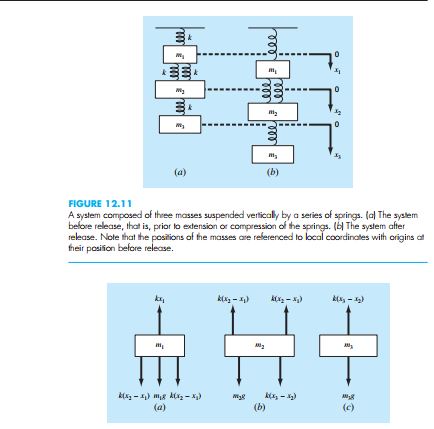
Pada pertemuan ini, memperdalami penggunaan openmodelica untuk penyelesaian matriks. Penyelesaiannya tugasnya seperti berikut berdasarkan contoh sebagai berikut.
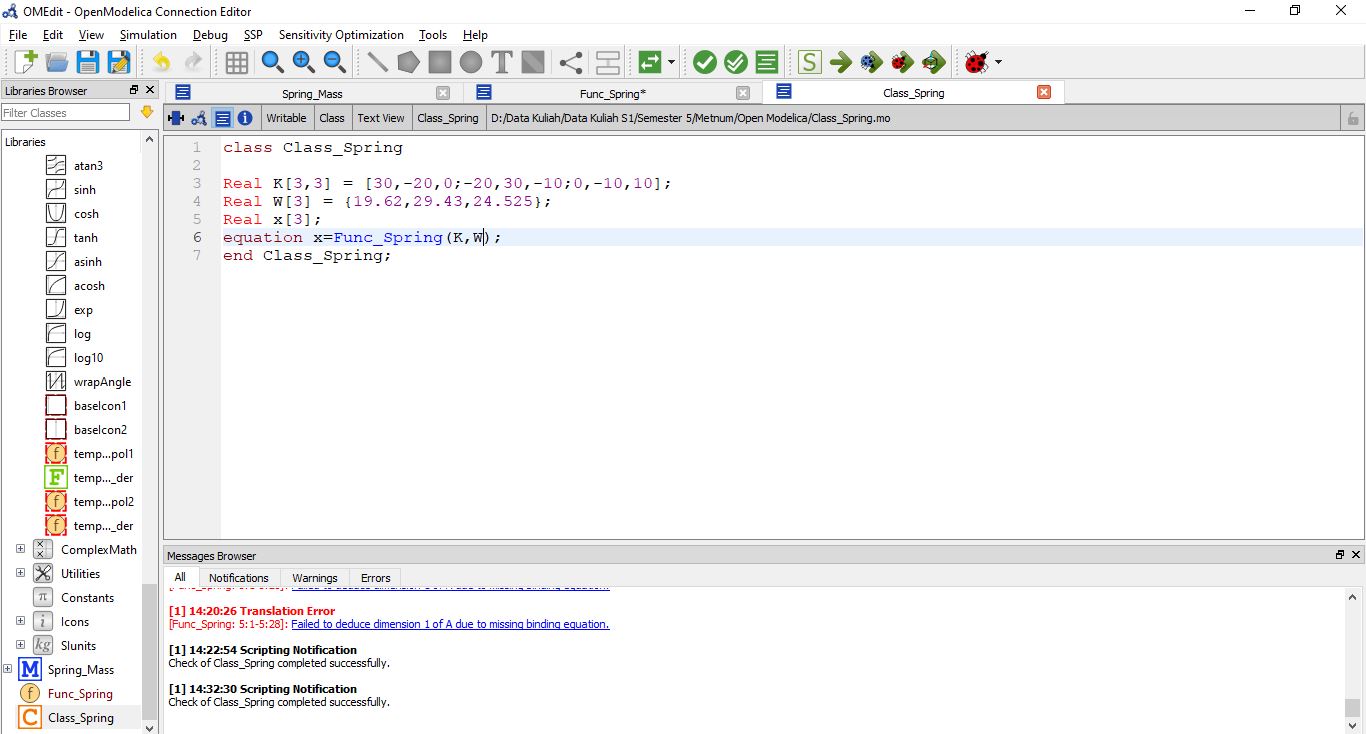
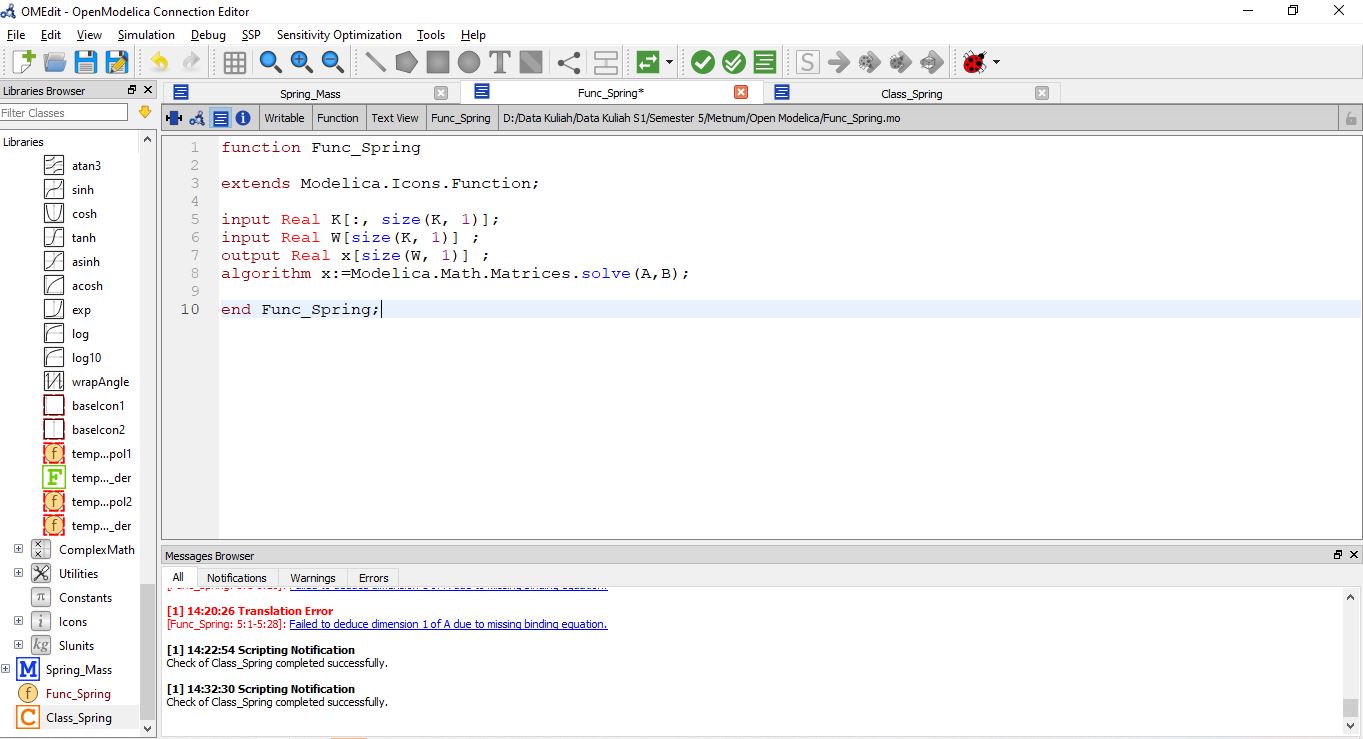
Lalu pada open modelica buka class and function sheet lalu masukan coding seperti dibawah ini.
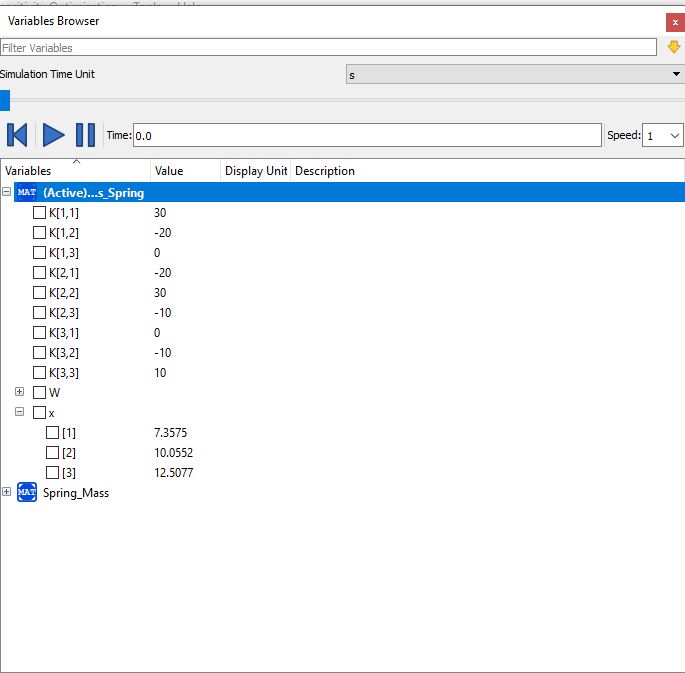
Dan berikut hasilnya.
Hasilnya sama seperti dengan dibuku.
TUGAS PERTEMUAN 3
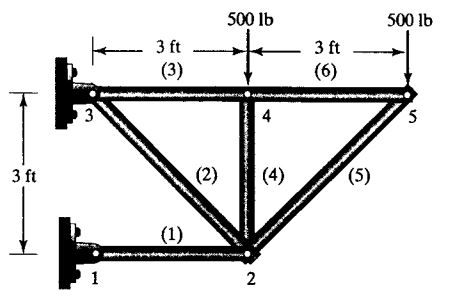
Berikut tugas yang diberikan pada pertemuan ini
Lalu kita tentukan node pada sistem tersebut. Sesuai gambar node pada sistem tersebut seperti tabel dibawah ini.
Lalu tentukan persamaan 'k'. karena pada beam 1,3,4,6 memiliki karakteristik yang sama. Maka dikelompokan menjadi k(1,3,4,6) dan k(2,5)
lalu masukan nilai k ke matriks seperti dibawah ini
karena sudut dari beam 1,3,6 = 0, sama maka matriks akan seperti ini. dan masukan ke matriks global maka akan jadi seperti ini. Lakukan hal yang sama pada setiap beamnya.
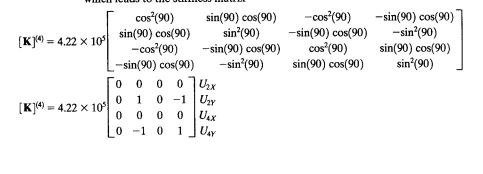
Untuk beam 4 gunakan persamaan ini
Untuk beam 2 dan 5 matriknya seperti ini.
Lalu semua matriks K 1 sampai K6 global ditambahkan menjadi matriks berikut dan lakukan eliminasi pada matriks
Lalu karena U1x, U1y, U3x dan U3y = 0 maka dapat disederhanakan menjadi seperti ini
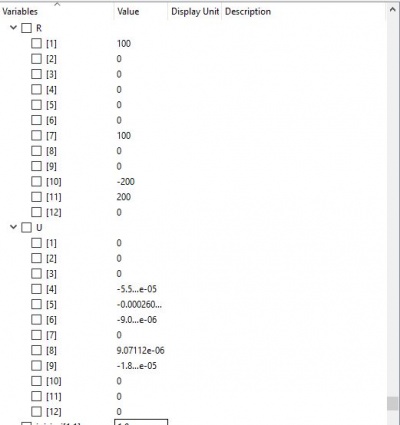
Lalu akan didapatkan hasil U seperti ini.
Lalu cari gaya gaya reaksinya
dan hasil akan seperti ini
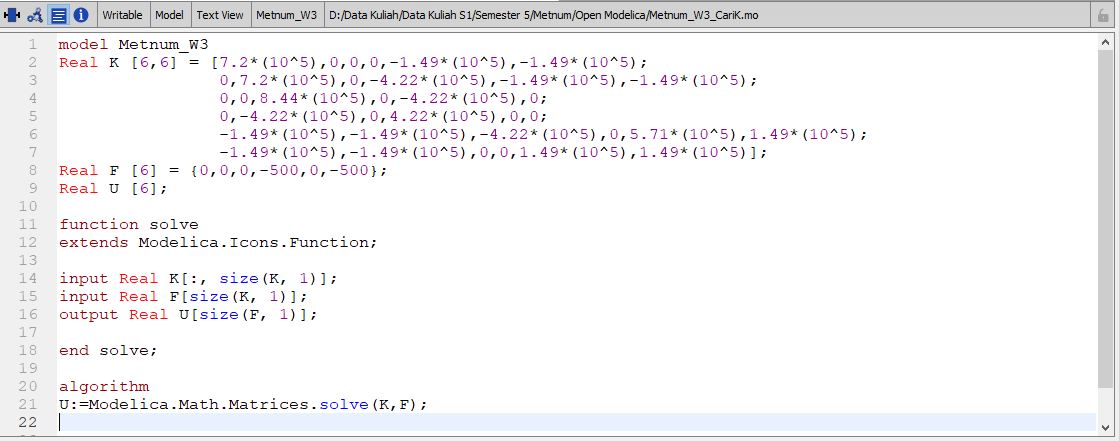
Dan berikut penyelesaiannya menggunakan Open Modelica. Berikut pada saat mencari K global
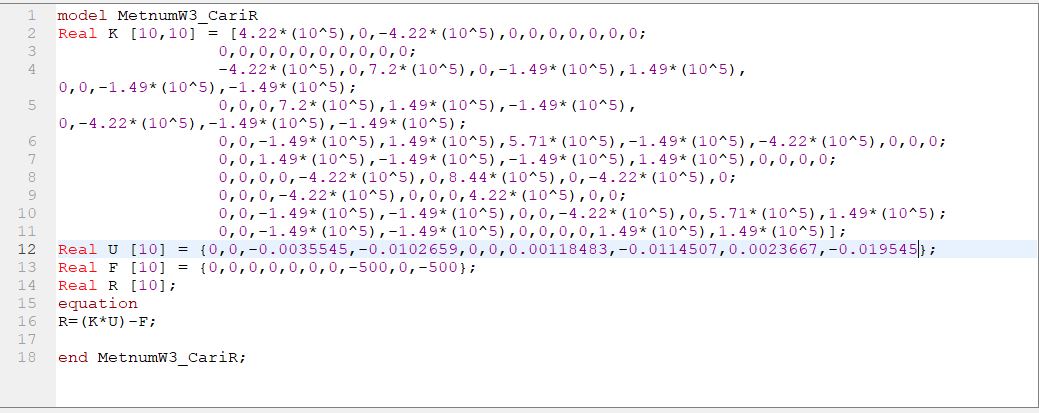
Berikut koding mencari R
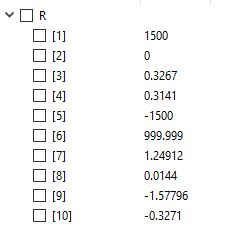
dan berikut hasilnya
Terjadi sedikit perbedaan karena pada dibuku ada nilai yang dibulatkan.
Pertemuan 4 (30 November 2020)
Quiz 2
Lalu flow perhitungannya
Nomor 4
Hal yang harus dilakukan pertama adalah menentukan node padasetiap batang dan menentukan nilai kekakuan pada batang. Lalu mencari K lokal di setiap batang. Satukan K lokal setiap batang menjadi K global.
Pada open modelica mencari ke kakuan setiap batang dan akan menemukan K lokal.
Lalu hasil K lokal digabungkan menjadi K global pada excel
Selanjutnya menghitung U dan R pada open modelica
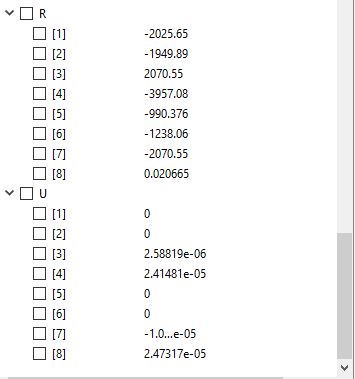
Dan berikut Hasil R dan Unya
Nomor 8
Untuk soal nomor 8 saya menggunakan coding dari josiah enrico. Dengan koding seperti berikut
Dan menghasilkan nilai seperti ini
Tapi menurut saya ada yang harus diperbaiki karena cosx, cos y dan cos z hanya 1 sedangkan cos dimasing sumbu harusnya ada 3. Jadi secara teoritis hasilnya akan salah. Saya akan mencoba mencari tahu bagaimana melakukan proses loop pada cos x, cos y dan cos z.
Pertemuan 5 (7 Desember 2020)
Pada pertemuan ke 5 pak dai menyuruh untuk belajar dengan berbagai macam fungsi di open modelica. Dan juga pak dai menyuruh dengan menyelesaikan soal dengan menggunakan berbagai rumus di open modelica seperti
-proses loooping
-data array
-fungsi if
-class dan memanggil function dalam modelica
Selanjutnya disuruh memahami koding yang dibuat oleh Ahmad Mohammad Fahmi.
TUGAS 4
Pada tugas ini saya bersama teman - teman yang lain melakukan diskusi dengan Ahmad Mohammad Fahmi dan cukup memahami alur dari pengerjaan.
1. Langkah 1 buat Class dengan memasukan semua parameter dan semua equation untuk menyelesaikan permasalahan.
2. Lalu membuat function matriks elemen
3. Lalu hasil dari matriks elemen di konversikan menjadi matriks global
4. Lalu tambahkan semua matriks global setiap elemen menjadi 1 matriks global dari semua elemen dengan fungsi sum
5. Cek setiap boundary di setiap poin
6. Lalu lakukan gauss jordan untuk mendapatkan K global Boundary
7. Hitung Reaction Force
8. Lakukan check force
9. Dan berikut Hasilnya
Pada koding ini saya masih belum terlalu mengerti fungsi dari boundary dan check force. Yang nantinya akan saya pelajari lebih lanjut
Pertemuan 6 (14 Desember 2020)
Assalamu'alaikum wr.wb. pada pertemuan ini pak DAI menginstruksikan mahasiswanya untuk melakukan muhasabah diri. Muhasabah yang dilakukan dengan terkait dengan kemampuan dalam melakukan metode numerik secara individu. Muhasabah ini juga membuat para mahasiswa menilai diri sendiri berdasarkan kemampuan individual pemahaman metode numerik selama ini.
Selanjutnya Christo menjelaskan konsep berpikir dalam melakukan metode numerik dengan alur berfikir mengenai soal-soal yang telah diberikan dan menjelaskannya ke teman-teman yang ada di kelas menggunakan software OpenModelica. Lalu Enrico dan Fahmi menjelaskan perbedaan dari konsep koding mereka. Selanjutnya pak Dai meminta kita agar mengkombinasikan koding dari josiah dan fahmy untuk tugas besar 2 kelas secara bersama - sama.
Pertemuan 7 (21 Desember 2020)
Bu Candra untuk mengajari kami terkait optimisasi. Optimisasi adalah suatu cara untuk mendapatkan yang paling optimal dari suatu permasalahan. Optimasi yang dijelaskan oleh Bu Chandra adalah mengenai optimasi Bracket Optimization using golden ratio. Penerapan optimasi menggunakan golden ratio ini diharapkan dapat diaplikasikan dalam mengerjakan tugas besar dalam menentukan stress maksimum yang masih saftey pada struktur dan harga yang dikeluarkan untuk digunakan pada struktur secara keseluruhan. Untuk hal tersebut, kekuatan material harus lebih kuat dari stress dari beban yaitu stress dari beban tersebut tidak boleh lebih besar 1/2 kali nya dari kekuatan material. Dalam optimisasi tersebut harus ada fungsi objektif dan ada konstrain/batasan/interval. Kemudian kami melakukan
Optimasi merupakan cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Optimasi yang dilakukan bergantung pada penentuan dua titik(misal xL dan xU) sehingga terdapat satu nilai maksimum atau minimum dari fungsi tersebut pada selang nilai xL dan xU. Berikut adalah langkah-langkah dalam menentukan nilai maksimum dari sebuah fungsi:
1. Menentukan batasan titik awal terendah (xL) dan tertinggi (xH)
2. Mendapatkan nilai x1 dan x2 dari golden ratio (d)
3. Menentukan xL dan xH berdasarkan nilai batasan maksimum dan minimal baru
4. Mendapatkan nilai x1 dan x2 baru lanjutkan langkah tersebut hingga mendapatkan nilai maksimum dari fungsi tersebut
selanjutnya untuk dapat menentukan nilai x1 dan x2 membutuhkan persamaan berikut:
d = akar5 - 1/2 x (xu-xl)
x1 = x1 + d
x2 = xu - d
Dalam melakukan optimasi sebuah fungsi dan menentukan nilai xL dan xU baru harus memeperhatikan syarat berikut:
- f(x1) > f(x2), domain sebelah kiri x2 dapat dieliminasi xL = x2 untuk iterasi berikutnya xu = xu lama
- f(x2) > f(x1), domain x sebelah kanan x1 dapat dieliminasi xu = x1 untuk iterasi berikutnya xL = xL lamasimulasi pengerjaan soal di
buku chapra. berikut adalah soal beserta penyelesaian yang ada di buku
Lalu berikut script pada open modelicanya
Lalu hasilnya adalah sebagai berikut.
Tugas Besar Metode Numerik
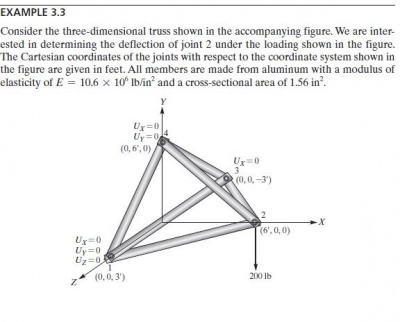
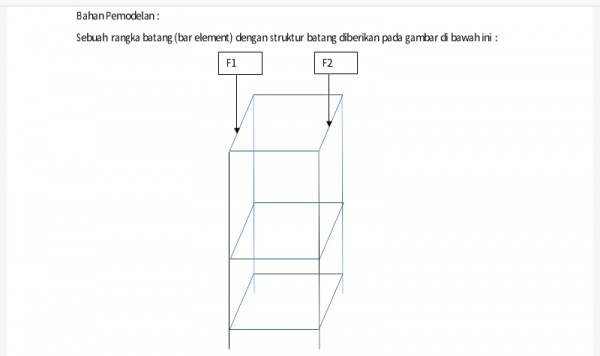
Pada tugas besar kali ini kami semua diperintahkan untuk menemukan cost yang paling optimal dengan variasi luas penampang pada batang dan jenis material berdasarkan modulus elastisitas nya dari soal berikut :
Constraint:
- Spesifikasi L (Panjang) dan geometri rangka truss
- Gaya beban terhadap struktur (1000 N dan 2000 N)
Asumsi:
- Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
- Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
Kode Modelica Pendukung:
|
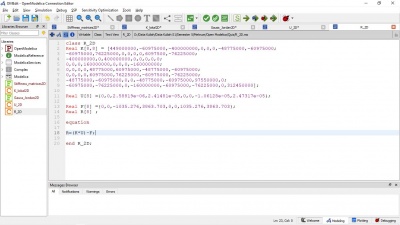
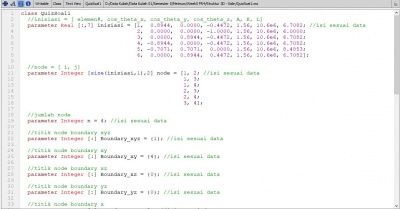
Trusses Modelling model Trusses_3D_Tugas_Besar_Safety //define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=250e6; //Yield Strength (Pa) Material ASTM A36 parameter Real Area=3.75E-04; //Area L Profile (0.04 x 0.04 x 0.005) (m2) parameter Real Elas=2e11; //Elasticity ASTM A36 (Pa) //define connection parameter Integer C[:,2]= [1,5; 2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 -0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0, 0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
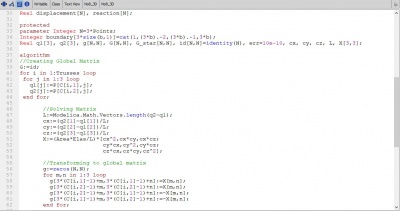
//solution Real displacement[N], reaction[N]; Real check[3]; Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3]; protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-6; algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for; //Implementing boundary for x in 1:Points loop if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
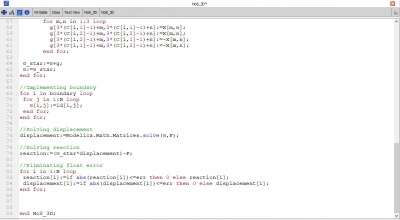
end for; //Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F); //Solving reaction reaction:=(G_star*displacement)-F; //Eliminating float error for i in 1:N loop reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; end for; //Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); for i in 1:3 loop check[i] := if abs(check[i])<=ers then 0 else check[i]; end for; //Calculating stress in each truss for i in 1:Trusses loop for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for; //Safety factor for i in 1:Trusses loop if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if; end for; end Trusses_3D_Tugas_Besar_Safety;
|
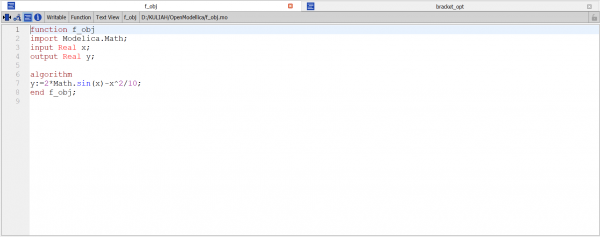
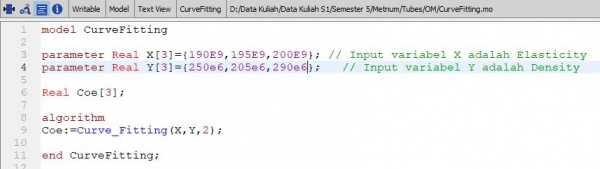
Curve Fitting Function function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting; |
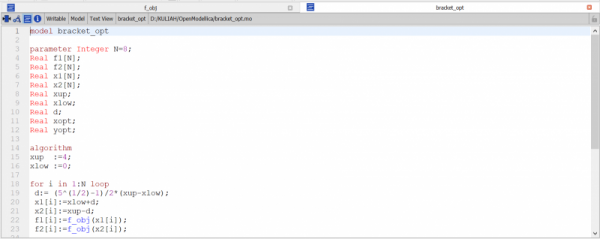
|
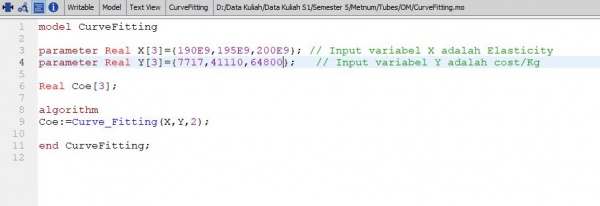
model CurveFitting parameter Real X[3]={190e9,195e9,200e9}; // Input variabel X adalah data bebas parameter Real Y[3]={7850,8020,8075}; // Input variabel Y adalah data berikat Real Coe[3]; algorithm Coe:=Curve_Fitting(X,Y,2); end CurveFitting; |
Modeling Trusses digunakan untuk mencari beberapa parameter seperti stress dan defleksi.
Sedangkan cuve fitting digunakan untuk mencari data - data yang belum didapatkan. Sama halnya seperti sistem regresi linear.
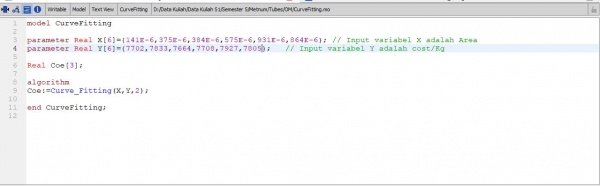
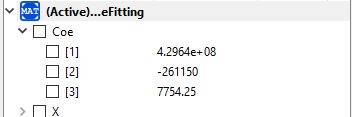
Dalam mencari curve fitting untuk material lock, maka input X adalah area dari siku pada setiap dimensi sedangkan Y adalah harga perkilogram dari siku. Berikut kodingan dan hasilnya.
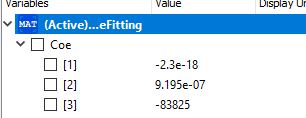
Berikut coding dari curve fitting untuk mencari harga perkilogram dari material lock ASTM A36
Dan berikut hasil dari coefficient
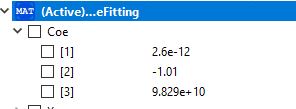
Berikut coding dari curve fitting untuk mencari harga perkilogram dari arealock pada dimensi 40 mm x 40 mm x 5 mm untuk material SS400, SS 304, SS316
Dan berikut hasil dari coefficient
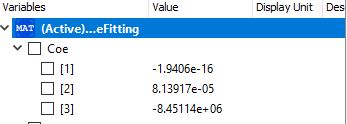
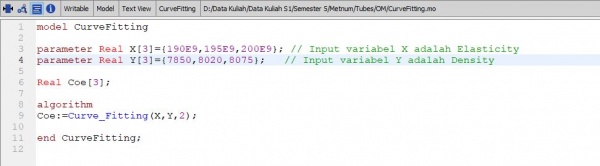
Berikut coding dari curve fitting untuk mencari density dari arealock pada dimensi 40 mm x 40 mm x 5 mm untuk material SS400, SS 304, SS316
Dan berikut hasil dari coefficient
Berikut coding dari curve fitting untuk mencari yield dari arealock pada dimensi 40 mm x 40 mm x 5 mm untuk material SS400, SS 304, SS316
Dan berikut hasil dari coefficient
Saat sudah melakukan curve fitting, maka optimasi kan. Berikut Coding Optimasi saaat di material lock.
model Opt_Gold
parameter Real xd[:]={111e-6,141e-6,171e-6,231e-6,304e-6,375e-6,344e-6,425e-6}; //Material Lock masukkin Area parameter Real yd[size(xd,1)]={269.3e-6,269.4e-6,269.6e-6,269.7e-6,269.8e-6,269.7e-6,269.8e-6,269.6e-6};//Ratio parameter Real xlo=111e-6;// x Low pada variabel x parameter Real xhi=425e-6; // x high pada variabel x parameter Integer N=100; // maximum iteration parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm xl := xlo; xu := xhi; y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
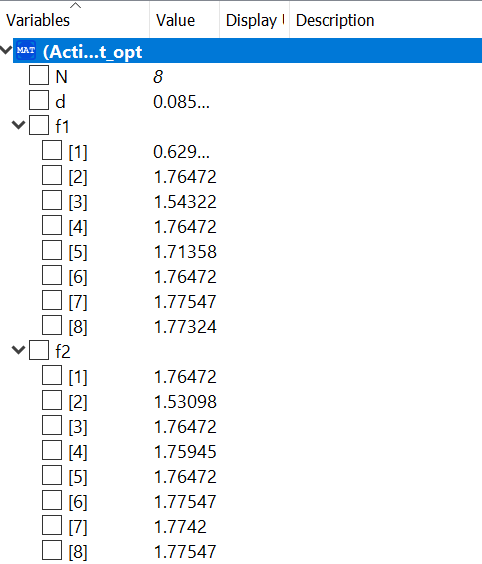
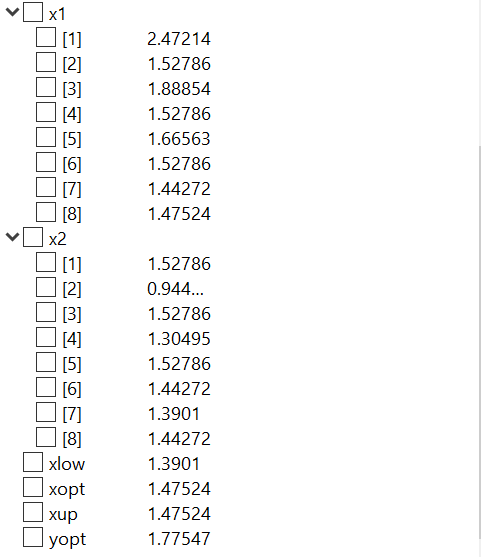
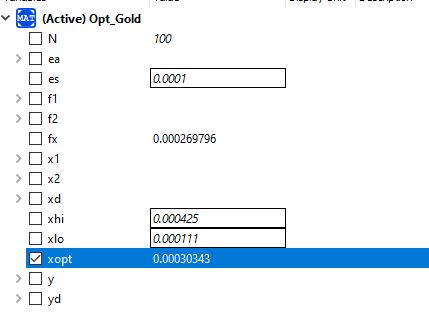
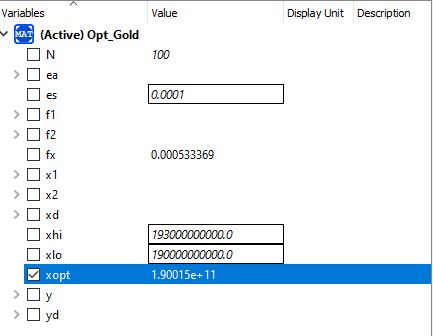
Berikut hasil dari optimasi material lock
Hasil optimasi menyatakan dimensi yang digunakan adalah 40 mm x 40 mm x 4 mm
Saat sudah melakukan curve fitting, maka optimasi kan. Berikut Coding Optimasi saaat di area lock.
model Opt_Gold
parameter Real xd[:]={190e9,191e9,192e9,193e9,194e9,195e9,196e9,197e9}; //Area Lock masukkin Elasticity parameter Real yd[size(xd,1)]={2.19e-4,1.02e-4,6.50e-5,4.77e-5,4.77e-5,3.3e-5,2.99e-5,284e-5};//Ratio parameter Real xlo=190e9;// x Low pada variabel x parameter Real xhi=197e9; // x high pada variabel x parameter Integer N=100; // maximum iteration parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm xl := xlo; xu := xhi; y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
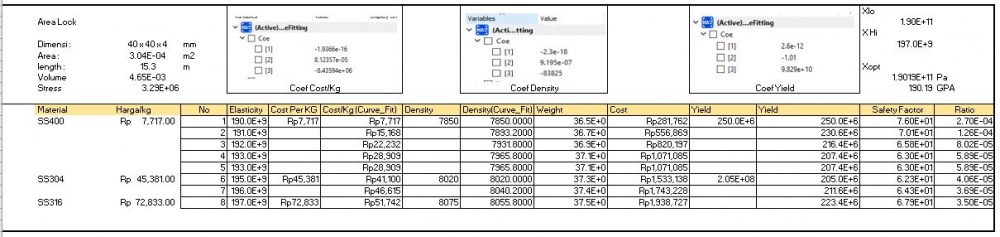
Berikut hasil dari optimasi area lock
Hasil optimasi menyatakan material yang digunakan adalah ASTM A36 atau SS 400.
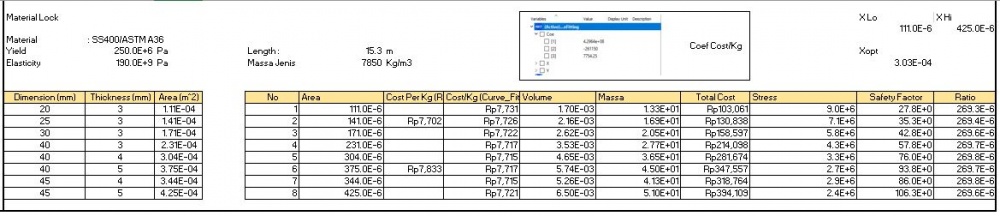
Data - data yang didapatkan diletakan di excel dan untuk material lock dengan material ASTM A36/ SS400 adalah sebagai berikut.
Lalu untuk area lock data yang didapatkan seperti berikut
Kesimpulan
Dari tugas besar melalui metode numerik, didapatkan hasil bahwa material yang digunakan adalah ASTM A36/SS 400 dengan dimensi 40 mm x 40 mm x 4mm dengan harga materialnya adalah Rp 281.762,-
UAS (Ujian Akhir Semester)
Pada tanggal 13 januari 2021 diadakan UAS. Berikut Jawaban UAS.
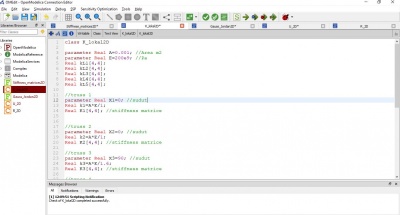
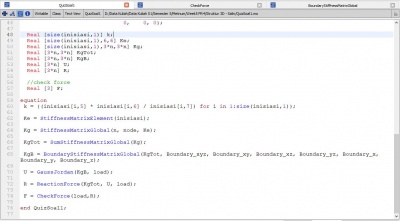
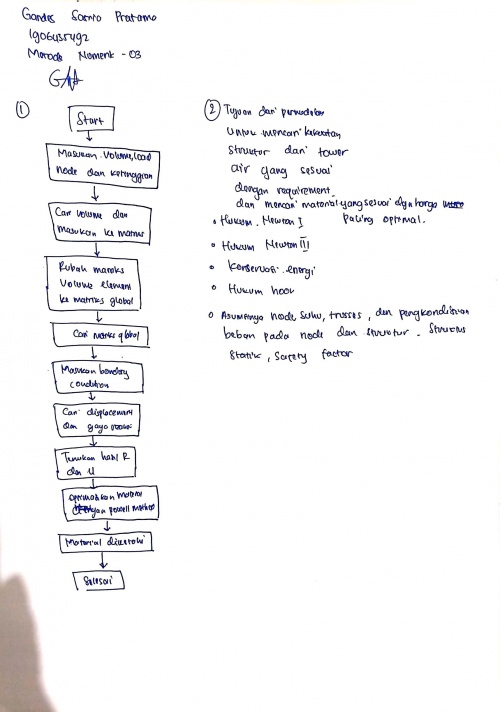
Jawaban No.1
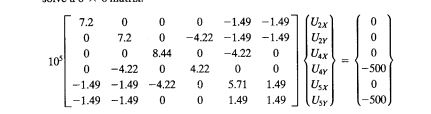
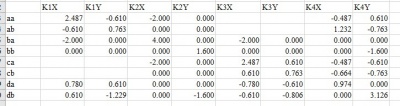
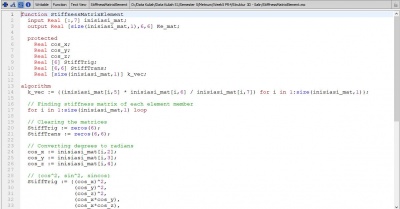
Jawaban Nomor 2
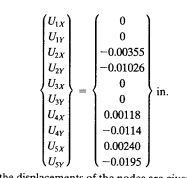
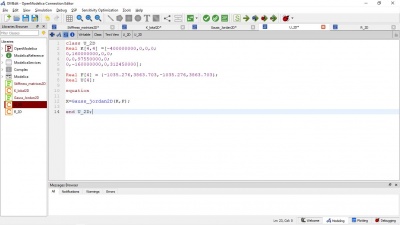
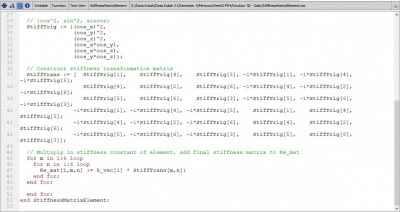
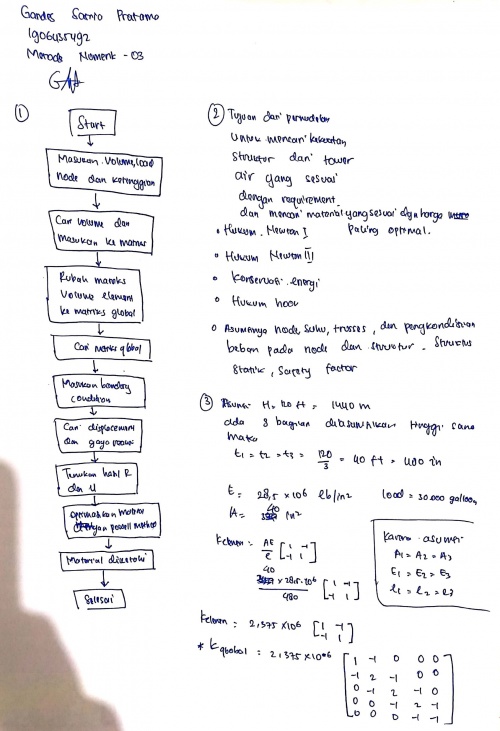
Jawaban Nomor 3
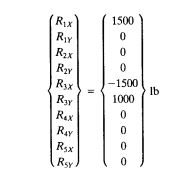
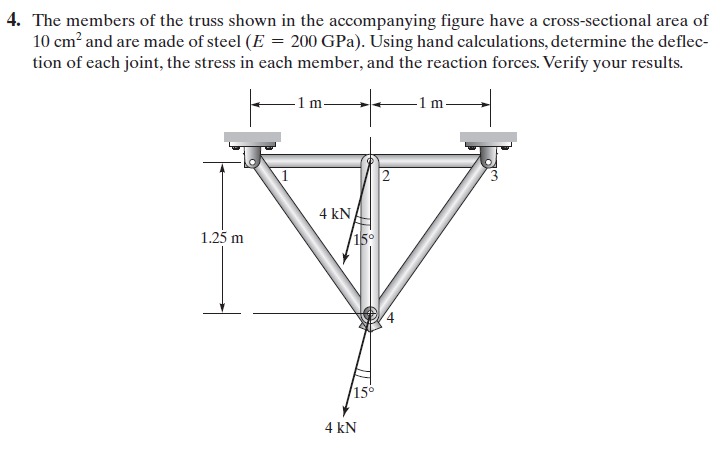
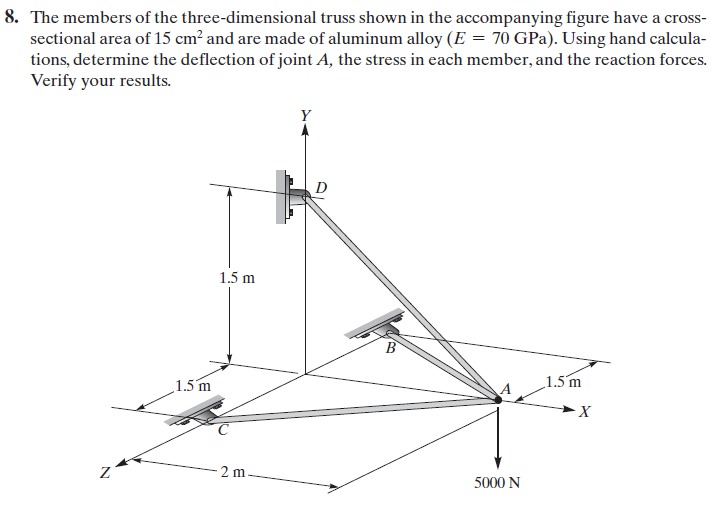
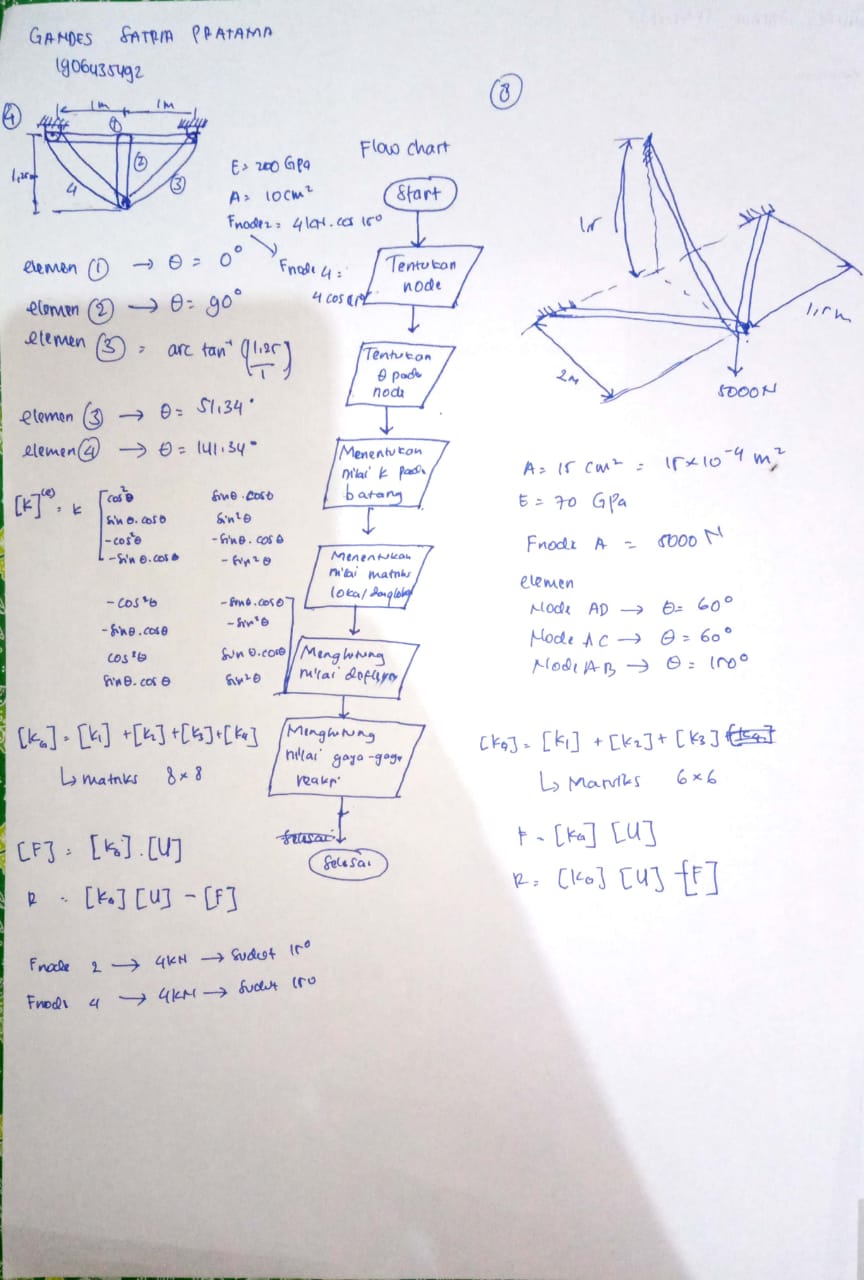
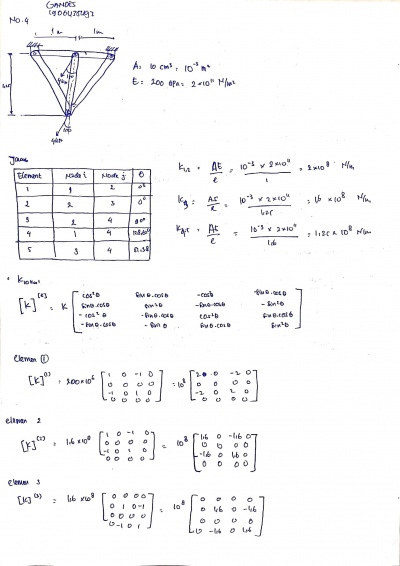
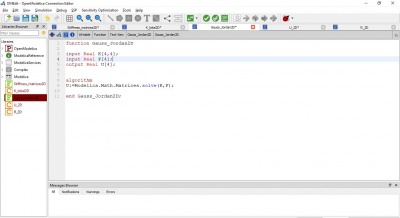
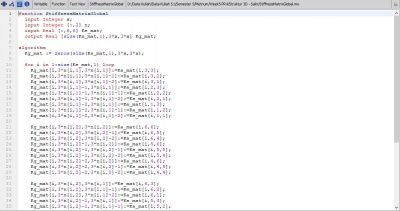
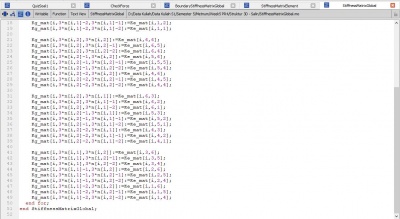
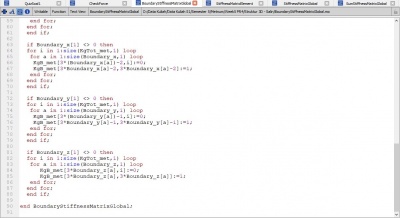
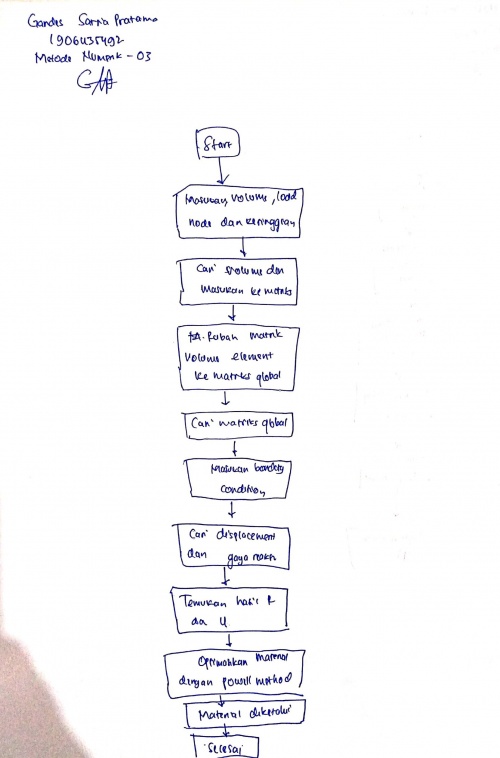
Jawaban Nomor 4,5,6
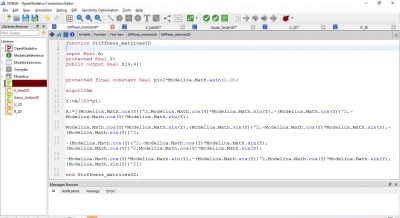
Codingan ---
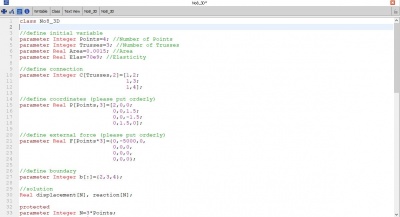
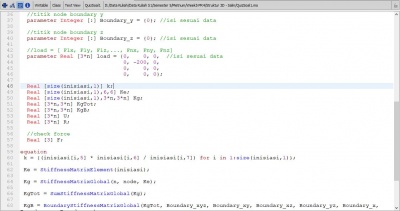
class UAS_Gandes parameter Real [:,5] inisiasi = [1,1, 2, 40, 28.5e6, 480;
1,1, 3, 40, 28.5e6, 480;
1,1, 4, 40, 28.5e6, 480];
parameter Integer [:,2] node = [1, 2;
1, 3;
1, 4];
parameter Integer y = size(node,1);
parameter Integer x = 2*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {3};
parameter Real [:,3] node_load = [1, 0, 2503621.3356 ;
2, 0, 0;
3, 0, 0];
parameter Real [2*(size(node_load,1))] load = {0,2503621.3356,0,0,0,0,0,0};
Real [y] k;
Real [y,4,4] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
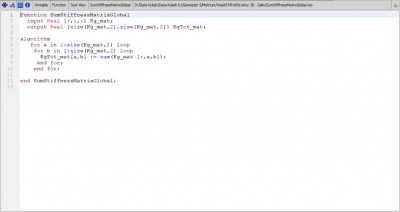
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
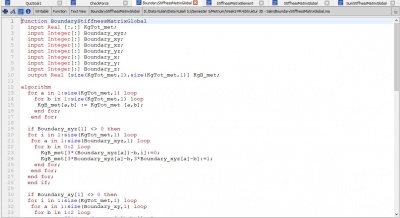
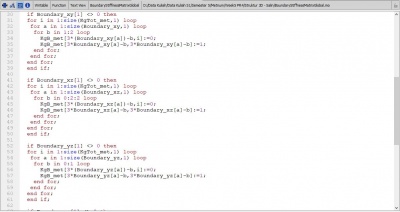
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
class UAS_Gandes