Muhammad Naufal Maulana

PERKENALAN SINGKAT

Saya Muhammad Naufal Maulana, mahasiswa teknik mesin UI angkatan 2019. Saya tertarik dengan teknik mesin karena memiliki prospek kerja yang luas. Materi yang sudah saya pelajari sebelum uts ini adalah mengenai turunan numerik, deret mclaurin , interpolasi, regresi, pengertian dari metode numerik, pseucode.

MINGGU KE 1

Tujuan mempelajari metode numerik

• Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik seperti:Persamaan algoritma, aljabar, pencocokan kurva, persamaan diferensial parsial, dan lainnya
• Mengerti dan mampu menerapkan pemahaman atau aplikasi terhadap konsep metode numerik
• Mampu menerapkan metode numerik dalam hal terkait persoalan keteknikan
• Mendapat added value (nilai tambah)/adab sehingga mahasiswa menjadi orang yang memiliki budi pekerti yang baik

TUGAS 1

Pada pertemuan sebelumnya, saya diberi tugas membuat video terkait penggunaan aplikasi open modelica. Berikut ini adalah hasil tugas saya:

MINGGU KE 2

Pertemuan kedua bersama Pak Dai, Kami diminta menjadi pribadi yang lebih baik dari hari kemarin. Setelah itu, kami diminta untuk mempresentasikan tugas kami sebelumnya. Setelah itu materi yang diberikan pada pertemuan ini adalah penggunaan class untuk memanggil sebuah function. Function yang bisa dipanggil beragam jumlahnya, mulai dari penjumlahan sederhana sampai operasi eliminasi matriks.

TUGAS 2

Di akhir kelas, kami diberi tugas untuk membuat video mengenai cara menyelesaikan persamaan aljabar simultan dengan OpenModelica, dengan metode yang telah diajarkan sebelumnya. Berikut ini adalah hasil tugas saya:

MINGGU KE 3

Pada pertemuan ketiga dilakukan pembahasan tentang penggunaan OpenModelica pada permasalahan engineering. Pada permasalahan engineering, metode numerik dapat membantu menyelesaikan persoalan lebih cepat. Contoh metode numerik yang dapat membantu menyelesaikan permasalaha engineering diantaranya Metode Stokastik, CFD(Computation fluid dynamics, dan FEA ( FInite Element Analaysis). Tahapan untuk menyelesaikan masalah engineering menggunakan metode numerik:

• 1. Melakukan analisis terhadap masalah engineering
• 2. Melakukan pemodelan matematis dari masalah yang sudah dianalisis
• 3. Menerjemahkan pemodelan matematis yang sudah dibuat menjadi metode numerik agar bisa dhitung oleh komputer
• 4. Melakukan perhitungan metode numerik menggunakan software dan dihasilkanlah solusi dari masalah engineering tersebut

TUGAS 3

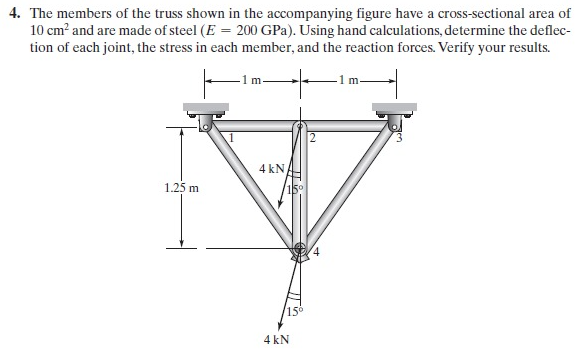
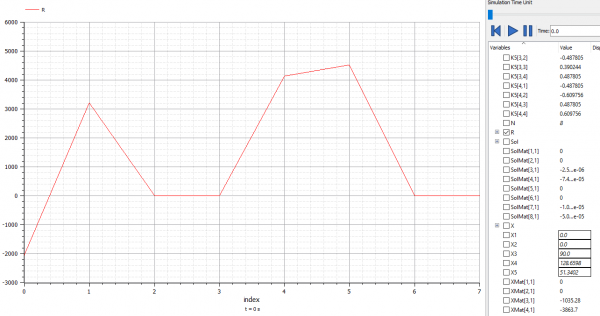
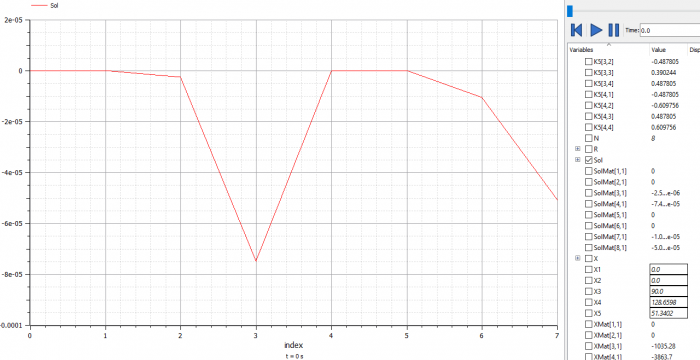
Mencari Truss Analysis menggunakan OpenModelica

Grafik Reaction Forces

Grafik Displacement

Persamaan class Trusses_HW parameter Integer N=8; //Global matrice = 2*points connected parameter Real A=0.001; //Area m2 parameter Real E=200e9; //Pa Real G[N,N]; //global Real Ginitial[N,N]; //global Real Sol[N]; //global dispplacement Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; Real R[N]; //global reaction force Real SolMat[N,1]; Real XMat[N,1]; //boundary condition Integer b1=1; Integer b2=3; //truss 1 parameter Real X1=0; //degree between truss Real k1=A*E/1; Real K1[4,4]; //stiffness matrice Integer p1a=1; Integer p1b=2; Real G1[N,N]; //truss 2 parameter Real X2=0; //degree between truss Real k2=A*E/1; Real K2[4,4]; //stiffness matrice Integer p2a=2; Integer p2b=3; Real G2[N,N]; //truss 3 parameter Real X3=90; //degree between truss Real k3=A*E/1.25; Real K3[4,4]; //stiffness matrice Integer p3a=2; Integer p3b=4; Real G3[N,N]; //truss 4 parameter Real X4=90+38.6598; //degree between truss Real k4=A*E/1.6; Real K4[4,4]; //stiffness matrice Integer p4a=1; Integer p4b=4; Real G4[N,N]; //truss 5 parameter Real X5=90-38.6598; //degree between truss Real k5=A*E/1.6; Real K5[4,4]; //stiffness matrice Integer p5a=3; Integer p5b=4; Real G5[N,N]; /* for each truss, please ensure pXa is lower then pXb (X represents truss element number) */ algorithm //creating global matrice K1:=Stiffness_Matrices(X1); G1:=k1*Local_Global(K1,N,p1a,p1b); K2:=Stiffness_Matrices(X2); G2:=k2*Local_Global(K2,N,p2a,p2b); K3:=Stiffness_Matrices(X3); G3:=k3*Local_Global(K3,N,p3a,p3b); K4:=Stiffness_Matrices(X4); G4:=k4*Local_Global(K4,N,p4a,p4b); K5:=Stiffness_Matrices(X5); G5:=k5*Local_Global(K5,N,p5a,p5b); G:=G1+G2+G3+G4+G5; Ginitial:=G; //implementing boundary condition for i in 1:N loop G[2*b1-1,i]:=0; G[2*b1,i]:=0; G[2*b2-1,i]:=0; G[2*b2,i]:=0; end for; G[2*b1-1,2*b1-1]:=1; G[2*b1,2*b1]:=1; G[2*b2-1,2*b2-1]:=1; G[2*b2,2*b2]:=1; //solving displacement Sol:=Gauss_Jordan(N,G,X); //solving reaction force SolMat:=matrix(Sol); XMat:=matrix(X); R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); end Trusses_HW;

Fungsi Panggil

Matrice Transformation function Stiffness_Matrices input Real A; Real Y; output Real X[4,4]; Real float_error = 10e-10; final constant Real pi=2*Modelica.Math.asin(1.0); algorithm Y:=A/180*pi; X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y); Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2; -(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y); -Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2]; for i in 1:4 loop for j in 1:4 loop if abs(X[i,j]) <= float_error then X[i,j] := 0; end if; end for; end for; end Stiffness_Matrices;

Global Element Matrice function Local_Global input Real Y[4,4]; input Integer B; input Integer p1; input Integer p2; output Real G[B,B]; algorithm for i in 1:B loop for j in 1:B loop G[i,j]:=0; end for; end for; G[2*p1,2*p1]:=Y[2,2]; G[2*p1-1,2*p1-1]:=Y[1,1]; G[2*p1,2*p1-1]:=Y[2,1]; G[2*p1-1,2*p1]:=Y[1,2]; G[2*p2,2*p2]:=Y[4,4]; G[2*p2-1,2*p2-1]:=Y[3,3]; G[2*p2,2*p2-1]:=Y[4,3]; G[2*p2-1,2*p2]:=Y[3,4]; G[2*p2,2*p1]:=Y[4,2]; G[2*p2-1,2*p1-1]:=Y[3,1]; G[2*p2,2*p1-1]:=Y[4,1]; G[2*p2-1,2*p1]:=Y[3,2]; G[2*p1,2*p2]:=Y[2,4]; G[2*p1-1,2*p2-1]:=Y[1,3]; G[2*p1,2*p2-1]:=Y[2,3]; G[2*p1-1,2*p2]:=Y[1,4]; end Local_Global;

Reaction Matrices Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses;

Gauss Jordan function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; Real float_error = 10e-10; algorithm X:=Modelica.Math.Matrices.solve(A,B); for i in 1:N loop if abs(X[i]) <= float_error then X[i] := 0; end if; end for; end Gauss_Jordan;

TUGAS BESAR

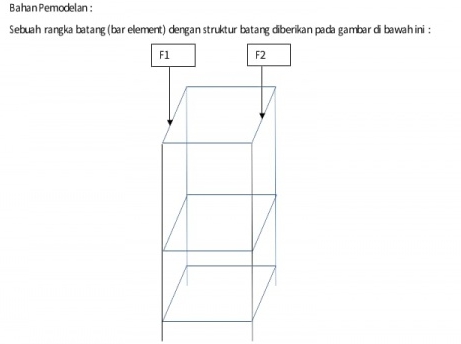
Tugas besar yang diberikan untuk kelas metnum 02 dan 03 adalah melakukan optimasi pada rangka sederhana:

Dengan data sebagai berikut:

Pada soal ini kami diharapkan dapat mendesain rangka batang dengan harga terjangkau dengan fungsi yang optimal.

Faktor atau variabel bebasnya meliputi : Harga, Material yang digunakan, cross section Dilakukan dengan metode optimasi dan membentuk curve fitting pada variabel harga