Difference between revisions of "Gigih Putro Pratomo"
Gigih.putro (talk | contribs) |
Gigih.putro (talk | contribs) |
||
| Line 36: | Line 36: | ||
Link Video [[https://youtu.be/1se3qKILbOI]] | Link Video [[https://youtu.be/1se3qKILbOI]] | ||
| + | |||
| + | |||
| + | == UAS Metode Numerik == | ||
| + | import math | ||
| + | def bracket(f,x1,h): | ||
| + | c = 1.618033989 | ||
| + | f1 = f(x1) | ||
| + | x2 = x1 + h | ||
| + | f2 = f(x2) | ||
| + | if f2 > f1: | ||
| + | return x2,x1 - h | ||
| + | for i in range (100): | ||
| + | h = c*h | ||
| + | x3 = x2 + h | ||
| + | f3 = f(x3) | ||
| + | if f3 > f2: | ||
| + | return x1,x3 | ||
| + | x1 = x2 | ||
| + | x2 = x3 | ||
| + | f1 = f2 | ||
| + | f2 = f3 | ||
| + | print ("bracket did not find a minimum") | ||
| + | def search(f,a,b,tol=1.0e-9): | ||
| + | nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a)))) | ||
| + | R = 0.618033989 | ||
| + | C = 1.0 - R | ||
| + | x1 = R*a + C*b | ||
| + | x2 = C*a + R*b | ||
| + | f1 = f(x1) | ||
| + | f2 = f(x2) | ||
| + | for i in range(nIter): | ||
| + | if f1 > f2: | ||
| + | a = x1 | ||
| + | x1 = x2 | ||
| + | f1 = f2 | ||
| + | x2 = C*a + R*b | ||
| + | f2 = f(x2) | ||
| + | else: | ||
| + | b = x2 | ||
| + | x2 = x1 | ||
| + | f2 = f1 | ||
| + | x1 = R*a + C*b | ||
| + | f1 = (x1) | ||
| + | if f1 < f2: | ||
| + | return x1,f1 | ||
| + | else: | ||
| + | return x2,f2 | ||
| + | print("aplikasi optimasi section modulus L stiffner") | ||
| + | print("kondisi terkait : lebar alas > lebar atas > lebar tengah") | ||
| + | b1 = eval(input("Nilai lebar bangun alas :")) | ||
| + | b3 = eval(input("Nilai lebar bangun atas :")) | ||
| + | b2 = eval(input("Nilai lebar bangun tengah :")) | ||
| + | H = eval(input("Nilai tinggi L stiffner :")) | ||
| + | def f(x): | ||
| + | A1 = b1*(H-x)/2 | ||
| + | A2 = b2*x | ||
| + | A3 = b3*(H-x)/2 | ||
| + | d1 = 1/2*(H-x)/2 | ||
| + | d2 = 1/2*x+(H-x)/2 | ||
| + | d3 = 3/4*(H-x)+x | ||
| + | I1 = 1/12*b1*((H-x)/2)**3 | ||
| + | I2 = 1/12*b2*x**3 | ||
| + | I3 = 1/12*b3*((H-x)/2)**3 | ||
| + | dc = H-(d1*A1+d2*A2+d3*A3)/(A1+A2+A3) | ||
| + | I = I1-A1*(d1-dc)**2+I2-A2*(d2-dc)**2+I3-A3*(d3-dc)**2 | ||
| + | Z = I/dc | ||
| + | return Z | ||
| + | xStart = 0.0 | ||
| + | h = 1.0 | ||
| + | x1,x2 = bracket(f,xStart,h) | ||
| + | y,fMin = search(f,x1,x2) | ||
| + | print("optimal sectional area =",-fMin) | ||
| + | print("sectional area awal" , f(H)) | ||
| + | A = -fMin/f(H)*100 | ||
| + | print ("efisiensi",A,"%") | ||
| + | input ("\nPress return to exit") | ||
| + | |||
| + | Link video: [http://https://youtu.be/0j-vFS2T7VU] | ||
Revision as of 01:36, 29 May 2019
Contents
Tugas 2
Untuk pengkodingan program Python dengan persamaan "ax + by = c" dan "px + qy = r" maka tahap-tahapnya adalah sebagai berikut:
import numpy as np
A = np.array([
[a, b, c] ])
B = np.array([
[p, q, r] ])
print (a + b)
print (a - b)
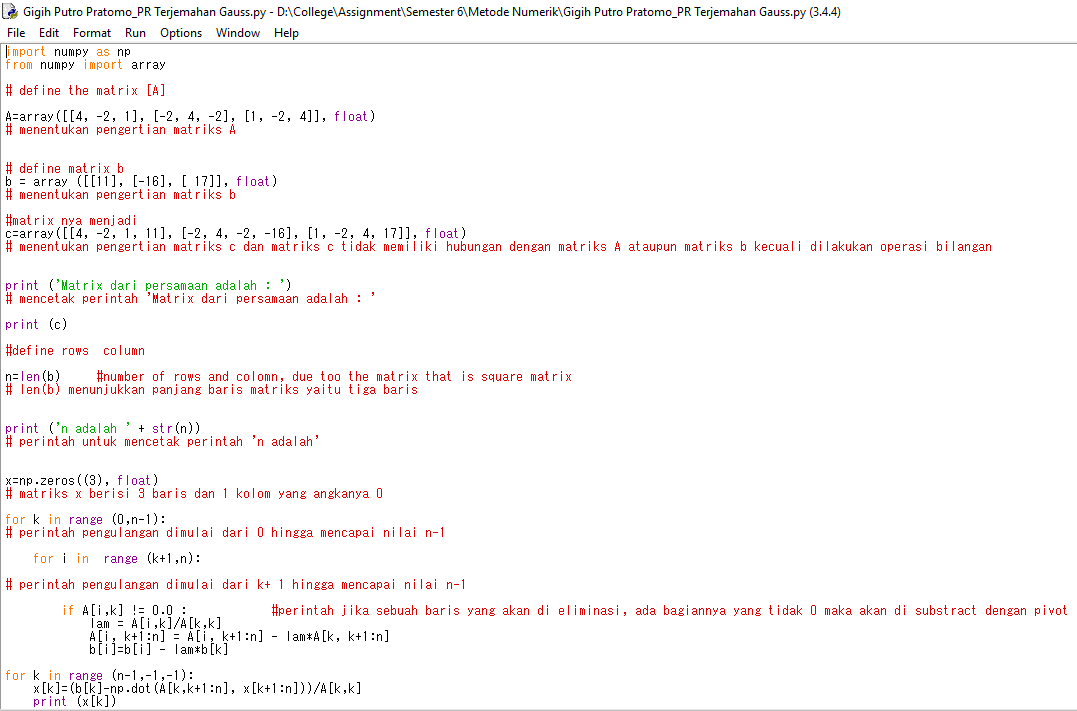
Latihan Metode Gauss
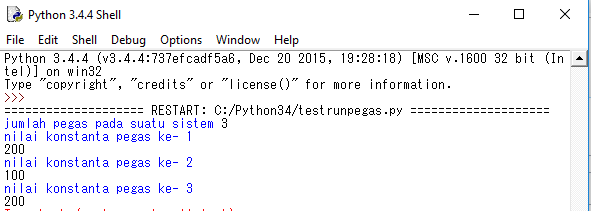
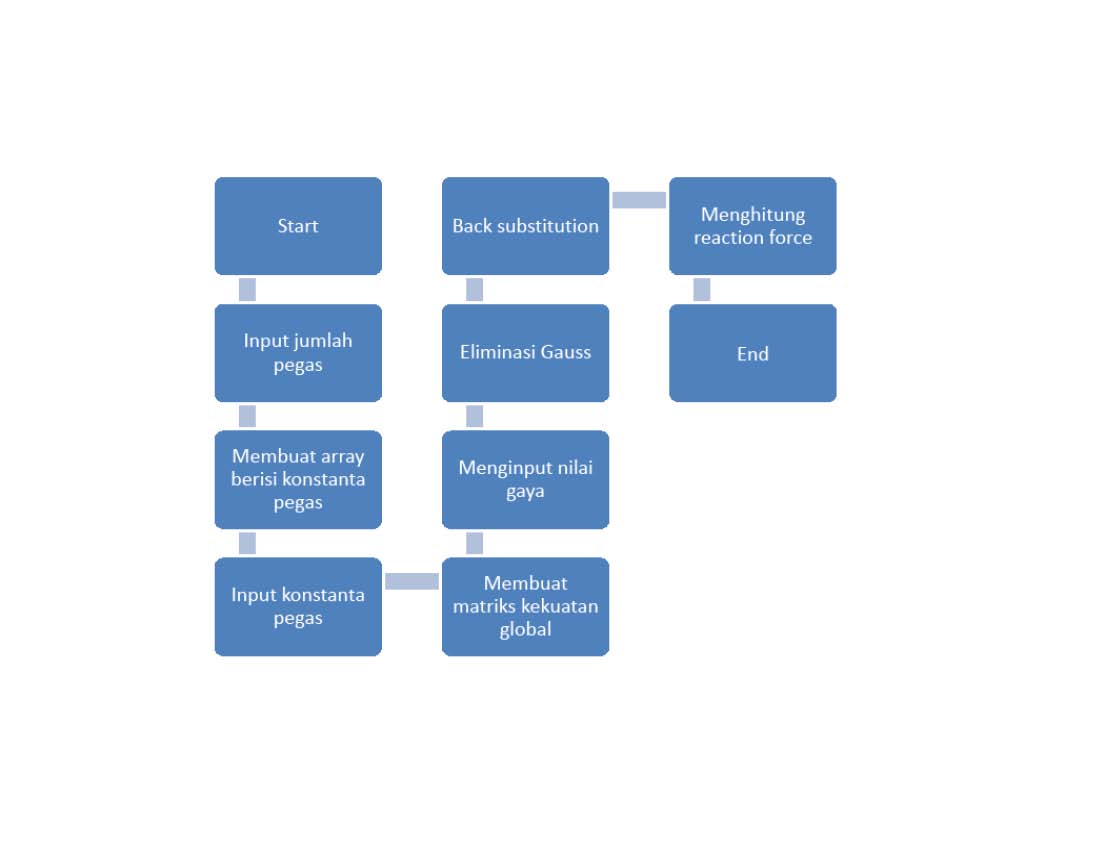
Tugas Kekakuan Pegas
Tugas 6 Metode Numerik
Link Video [[1]]
UAS Metode Numerik
import math def bracket(f,x1,h):
c = 1.618033989
f1 = f(x1)
x2 = x1 + h
f2 = f(x2)
if f2 > f1:
return x2,x1 - h
for i in range (100):
h = c*h
x3 = x2 + h
f3 = f(x3)
if f3 > f2:
return x1,x3
x1 = x2
x2 = x3
f1 = f2
f2 = f3
print ("bracket did not find a minimum")
def search(f,a,b,tol=1.0e-9):
nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a))))
R = 0.618033989
C = 1.0 - R
x1 = R*a + C*b
x2 = C*a + R*b
f1 = f(x1)
f2 = f(x2)
for i in range(nIter):
if f1 > f2:
a = x1
x1 = x2
f1 = f2
x2 = C*a + R*b
f2 = f(x2)
else:
b = x2
x2 = x1
f2 = f1
x1 = R*a + C*b
f1 = (x1)
if f1 < f2:
return x1,f1
else:
return x2,f2
print("aplikasi optimasi section modulus L stiffner") print("kondisi terkait : lebar alas > lebar atas > lebar tengah") b1 = eval(input("Nilai lebar bangun alas :")) b3 = eval(input("Nilai lebar bangun atas :")) b2 = eval(input("Nilai lebar bangun tengah :")) H = eval(input("Nilai tinggi L stiffner :")) def f(x):
A1 = b1*(H-x)/2 A2 = b2*x A3 = b3*(H-x)/2 d1 = 1/2*(H-x)/2 d2 = 1/2*x+(H-x)/2 d3 = 3/4*(H-x)+x I1 = 1/12*b1*((H-x)/2)**3 I2 = 1/12*b2*x**3 I3 = 1/12*b3*((H-x)/2)**3 dc = H-(d1*A1+d2*A2+d3*A3)/(A1+A2+A3) I = I1-A1*(d1-dc)**2+I2-A2*(d2-dc)**2+I3-A3*(d3-dc)**2 Z = I/dc return Z
xStart = 0.0 h = 1.0 x1,x2 = bracket(f,xStart,h) y,fMin = search(f,x1,x2) print("optimal sectional area =",-fMin) print("sectional area awal" , f(H)) A = -fMin/f(H)*100 print ("efisiensi",A,"%") input ("\nPress return to exit")
Link video: [2]