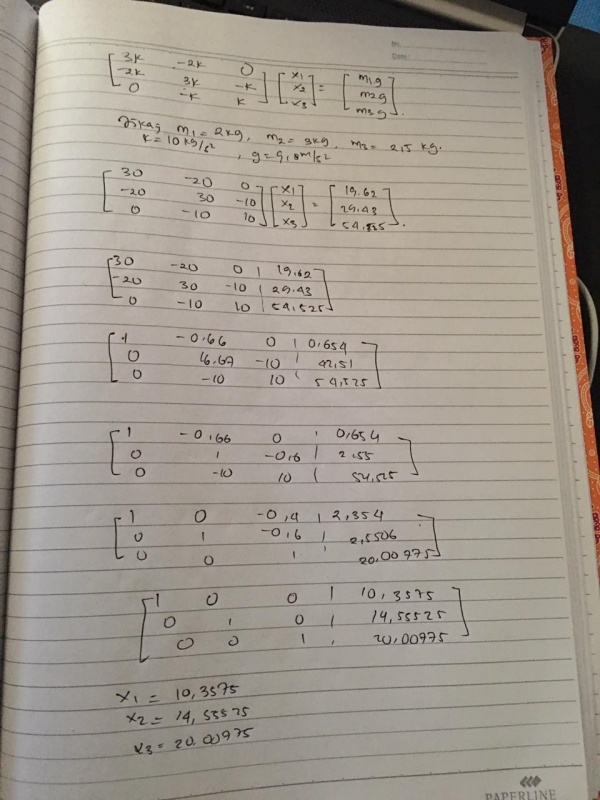Difference between revisions of "Metnum03 - Elita Kabayeva"
(→PENYELESAIAN MANUAL KUIS) |
|||
| Line 569: | Line 569: | ||
end Quiz8; | end Quiz8; | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | == TUGAS PERTEMUAN V == | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | |||
| + | ''Calculate Length and Cosine'' | ||
| + | class Length_Cos | ||
| + | |||
| + | parameter Integer Points=4; | ||
| + | parameter Integer Trusses=6; | ||
| + | parameter Integer C[Trusses,2]=[1,2; | ||
| + | 1,3; | ||
| + | 1,4; | ||
| + | 2,3; | ||
| + | 3,4; | ||
| + | 2,4]; | ||
| + | parameter Integer P[:,3]=[0,0,3; | ||
| + | 6,0,0; | ||
| + | 0,0,-3; | ||
| + | 0,6,0]; | ||
| + | |||
| + | //Element 1,4,5 | ||
| + | Real L1 [size(P,1)-1]; | ||
| + | Real cosx1 [size(P,1)-1]; | ||
| + | Real cosy1 [size(P,1)-1]; | ||
| + | Real cosz1 [size(P,1)-1]; | ||
| + | |||
| + | //Element 2 6 | ||
| + | Real L2 [size(P,1)-2]; | ||
| + | Real cosx2 [size(P,1)-2]; | ||
| + | Real cosy2 [size(P,1)-2]; | ||
| + | Real cosz2 [size(P,1)-2]; | ||
| + | |||
| + | //Element 3 | ||
| + | Real L3 [size(P,1)-3]; | ||
| + | Real cosx3 [size(P,1)-3]; | ||
| + | Real cosy3 [size(P,1)-3]; | ||
| + | Real cosz3 [size(P,1)-3]; | ||
| + | |||
| + | equation | ||
| + | //Element 1 4 5 | ||
| + | for i in 1:1:(size(P,1)-1) loop | ||
| + | L1[i] = sqrt((P[i+1,1]-P[i,1]^2+(P[i+1,2]-P[i,2])^2+(P[i+1,3]-P[i,3])^2)); | ||
| + | end for; | ||
| + | for i in 1:(size(P,1)-1) loop | ||
| + | cosx1 [i] = (P[i+1,1]-P[i,1])/L1[i]; | ||
| + | cosy1 [i] = (P[i+1,2]-P[i,2])/L1[i]; | ||
| + | cosz1 [i] = (P[i+1,3]-P[i,3])/L1[i]; | ||
| + | end for; | ||
| + | |||
| + | //Element 2 6 | ||
| + | for i in 1:1:(size(P,1)-2) loop | ||
| + | L2 [i] = sqrt((P[i+2,1]-P[i,1]^2+(P[i+2,2]-P[i,2])^2+(P[i+2,3]-P[i,3])^2)); | ||
| + | end for; | ||
| + | for i in i:(size(P,1)-2) loop | ||
| + | cosx2 [i] = (P[i+2,1]-P[i,1])/L2[i]; | ||
| + | cosy2 [i] = (P[i+2,2]-P[i,2])/L2[i]; | ||
| + | cosz2 [i] = (P[i+2,3]-P[i,3])/L2[i]; | ||
| + | end for; | ||
| + | |||
| + | //Element 3 | ||
| + | for i in 1:1:(size(P,1)-3) loop | ||
| + | L3 [i] = sqrt((P[i+3,1]-P[i,1]^2+(P[i+3,2]-P[i,2])^2+(P[i+3,3]-P[i,3])^2)); | ||
| + | end for; | ||
| + | for i in i:(size(P,1)-3) loop | ||
| + | cosx3 [i] = (P[i+3,1]-P[i,1])/L3[i]; | ||
| + | cosy3 [i] = (P[i+3,2]-P[i,2])/L3[i]; | ||
| + | cosz3 [i] = (P[i+3,3]-P[i,3])/L3[i]; | ||
| + | end for; | ||
| + | end Length_Cos; | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | '''MASTER CODE (CLASS)''' | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | ||
| + | class Soal5 | ||
| + | //inisiasi = [ elemen#, dX, dY, dZ, A, E] | ||
| + | parameter Real [:,6] inisiasi = [1, 0.8944, 0.0000, -0.4472, 1.56, 10.6e6; //isi sesuai data | ||
| + | 2, 0.0000, 0.0000, -1.0000, 1.56, 10.6e6; | ||
| + | 3, 0.0000, 0.8944, -0.4472, 1.56, 10.6e6; | ||
| + | 4, -0.8944, 0.0000, -0.4472, 1.56, 10.6e6; | ||
| + | 5, -0.7071, 0.7071, 0.0000, 1.56, 10.6e6; | ||
| + | 6, 0.0000, 0.8944, 0.4472, 1.56, 10.6e6]; | ||
| + | |||
| + | //node = [ i, j] | ||
| + | parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data | ||
| + | 1, 3; | ||
| + | 1, 4; | ||
| + | 2, 3; | ||
| + | 2, 4; | ||
| + | 3, 4]; | ||
| + | |||
| + | //jumlah node | ||
| + | parameter Integer n = 4; //isi sesuai data | ||
| + | |||
| + | //titik node boundary xyz | ||
| + | parameter Integer [:] Boundary_xyz = {1,3,4}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary xy | ||
| + | parameter Integer [:] Boundary_xy = {3}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary xz | ||
| + | parameter Integer [:] Boundary_xz = {0}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary yz | ||
| + | parameter Integer [:] Boundary_yz = {0}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary x | ||
| + | parameter Integer [:] Boundary_x = {2}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary y | ||
| + | parameter Integer [:] Boundary_y = {4}; //isi sesuai data | ||
| + | |||
| + | //titik node boundary z | ||
| + | parameter Integer [:] Boundary_z = {1}; //isi sesuai data | ||
| + | |||
| + | //load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz] | ||
| + | parameter Real [3*n] load = {0, 0, 0, //isi sesuai data | ||
| + | 0, -200, 0, | ||
| + | 0, 0, 0, | ||
| + | 0, 0, 0}; | ||
| + | |||
| + | Real [size(inisiasi,1)] L; | ||
| + | Real [size(inisiasi,1)] k; | ||
| + | Real [size(inisiasi,1),6,6] Ke; | ||
| + | Real [size(inisiasi,1),3*n,3*n] Kg; | ||
| + | Real [3*n,3*n] KgTot; | ||
| + | Real [3*n,3*n] KgB; | ||
| + | Real [3*n] U; | ||
| + | Real [3*n] R; | ||
| + | |||
| + | //check force | ||
| + | Real [3] F; | ||
| + | |||
| + | equation | ||
| + | L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)}; | ||
| + | |||
| + | k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)}; | ||
| + | |||
| + | Ke = StiffnessMatrixElement(inisiasi); | ||
| + | |||
| + | Kg = StiffnessMatrixGlobal(n, node, Ke); | ||
| + | |||
| + | KgTot = SumStiffnessMatrixGlobal(Kg); | ||
| + | |||
| + | KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z); | ||
| + | |||
| + | U = GaussJordan(KgB, load); | ||
| + | |||
| + | R = ReactionForce(KgTot, U, load); | ||
| + | |||
| + | F = CheckForce(load,R); | ||
| + | |||
| + | |||
| + | end Soal5; | ||
|} | |} | ||
Revision as of 12:59, 14 December 2020
Contents
BIODATA
Nama : Elita Kabayeva
NPM : 1906435486
Pendidikan Terakhir : D-III
PERTEMUAN I (9/11/2020)
Dalam pertemuan pertama ini, pak Ahmad Indra melakukan review mengenai materi-materi yang telah dipelajari sebelum UTS. Sekaligus memberikan tugas untuk membuat video mengenai pembelajaran metode numerik yang saya lakukan menggunakan software OPENMODELICA. Materi yang diajarkan sebelum UTS adalah sebagai berikut Materi yang diajarkan sebelum UTS adalah sebagai berikut
1. Deret Taylor dan Deret Mclaurin
2. Pencarian Akar (Open Methods dan Bracketing)
Pada open methods diajarkan menggunakan Newton Rhapson, Simple Fix Point dan Secant Method. Sedangkan pada metode bracketing diajarkan menggunakan False methods dan Bisections.
3. Penurunan Numeric Pada penurunan ini kita diajarkan penurunan secara backward, forward dan center.
4. Regresi Linear dan Interpolasi
5. Gauss-Jordan dan Aljabar
Untuk video pembelajaran tersebut saya upload pada link Youtube berikut.
OPENMODELICA (PENYELESAIAN SISTEM PERSAMAAN PANGKAT TIGA, TIGA VARIABEL
Video diatas adalah perbaikan dari video sebelumnya yang telah saya upload di Youtube. Dikarenakan, video yang sebelumnya terdapat error pada audionya.
PERTEMUAN II (16/11/2020)
Pada pertemuan kedua ini, saya izin tidak mengikuti kelas sinkron melalui Zoom dikarenakan sakit. Namun, saya tetap melakukan pembelajaran mandiri setelahnya dengan membaca rangkuman dari teman-teman sekelas serta mencoba melakukan simulasi pencarian mean dengan menggunakan coding pada OPENMODELICA, sesuai dengan materi yang dilaksanakan pada Zoom di pertemuan kedua.
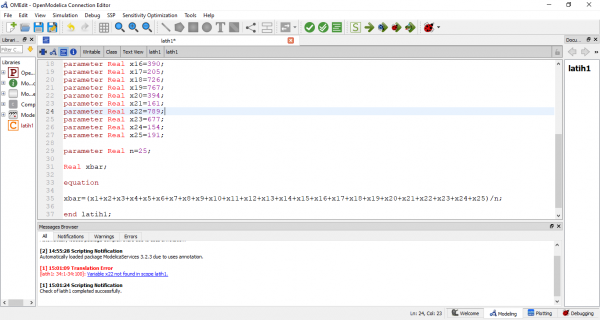
Diatas adalah coding OPENMODELICA untuk mencari mean. Disini saya menggunakan 25 data angka riil.
Setelah melakukan coding, saya mengecek apakah coding tersebut benar atau tidak.
Baru kemudian melakukan simulasi.
Berikut adalah hasil dari simulasi yang menyatakan nilai mean dari 25 data yang di input kan.
TUGAS PERTEMUAN II
Dalam pertemuan II kemarin, pak Dai memberi tugas untuk menyelesaikan persamaan aljabar simultan dengan menggunakan Gauss-Elimination, Gauss Seidel ataupun metoda lain.
Saya akan menggunakan metoda Gauss-Elimination untuk menyelesaikan persamaan aljabar berikut:
x1 + 2x2 + 3x3 + x4 = 9
3x1 + 5x2 + 7x3 + 4x4 = 12
4x1 + x2 + x3 + 3x4 = 23
6x1 + 7x2 + 5x3 + 2x4 = 0
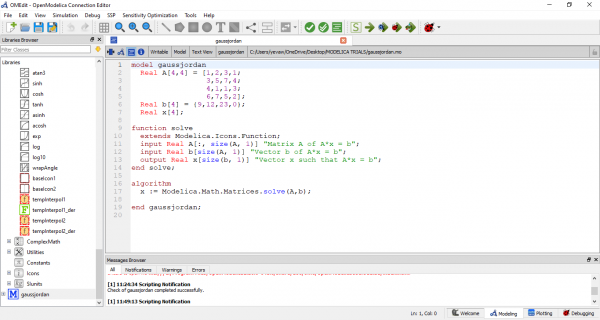
Berikut adalah hasil input coding saya pada OpenModelica untuk membentuk matriks dari persamaan-persamaan tersebut. Untuk coding, saya menggunakan perintah yang ada di library modelica yaitu "Modelica.Math.Matrices.solve(A,b)" untuk menyelesaikan sistem persamaan linier eliminasi gauss yang ada diatas.
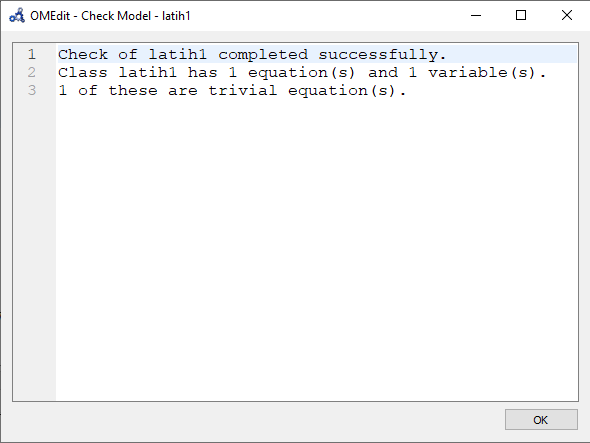
Kemudian, setelah melakukan input, saya melakukan pengecekan coding.
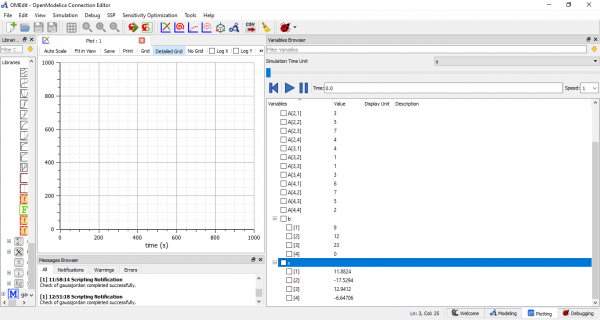
Setelah dilakukan simulasi, berikut adalah hasil untuk penyelesaian Eliminasi Gauss terhadap persamaan-persamaan diatas.
Hasilnya :
X1 = 11.8824
X2 = -17.5294
X3 = 12.9412
X4 = -6.64706
PERTEMUAN III (23/11/2020)
Pada pertemuan hari ini, pak Dai memberi tugas untuk menyelesaikan persoalan pegas yang terdapat pada bab 12 dari buku Numerical Method (Steven Chapras) dan membuktikan secara matematis hasil dari penyelesaian tersebut.
Saya melakukan perhitungan matematis terlebih dahulu dengan pertama-tama membuat Free Body Diagram dari masing-masing spring mass system yang ada di buku dan kemudian menuliskan persamaannya.
Kemudian dari persamaan tersebut, saya membuat bentuk matriks dan menyelesaikannya dengan metode Gauss-Jordan.
Dari Gauss-Jordan, saya mendapatkan hasil :
x1 = 10.3575 x2 = 14.55525 x3 = 20.00775
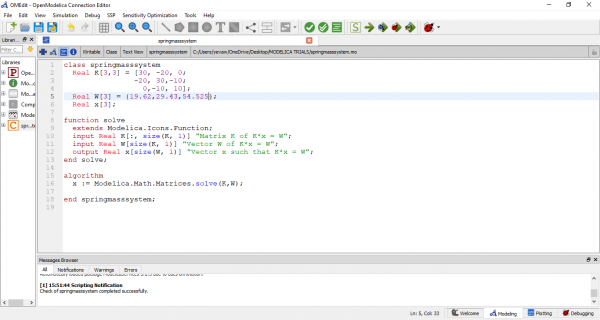
Kemudian setelah melakukan pembuktian secara matematis, saya menggunakan OpenModelica untuk menyelesaikan persoalan tersebut. Berikut adalah coding yang saya lakukan di OpenModelica.
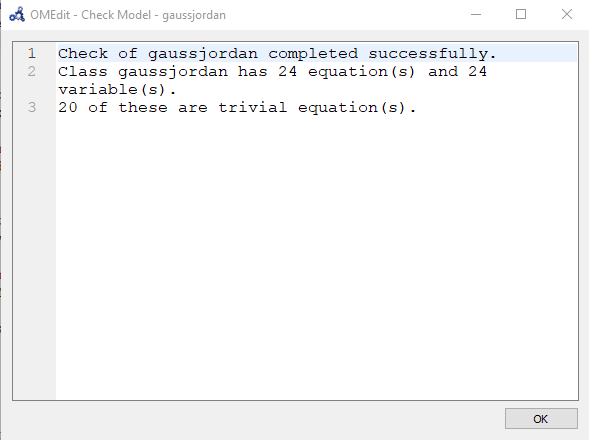
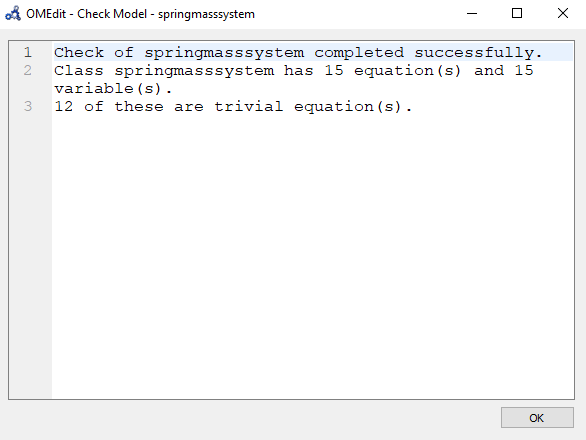
Lalu, saya melakukan verifikasi pengecekan coding.
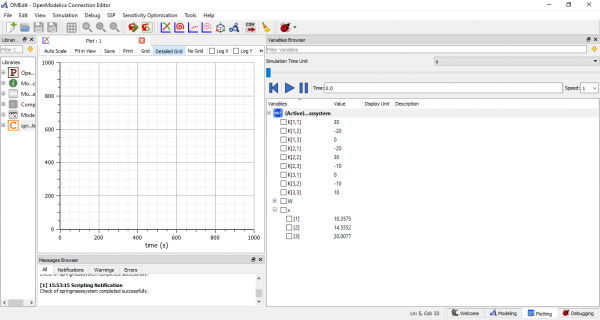
Setelah itu, saya simulate coding dan mendapatkan hasil sebagai berikut.
Dari simulasi pada OpenModelica, nilai x yang saya dapatkan adalah sebagai berikut :
x1 = 10.3575
x2 = 14.5552
x3 = 20.0077
Bisa dilihat bahwa dari pembuktian secara matematis maupun dari penyelesaian menggunakan simulasi OpenModelica, nilai dari X yang didapatkan bisa dikatakan sama (dengan perbedaan pada ketelitian dan angka dibelakang koma).
TUGAS PERTEMUAN III
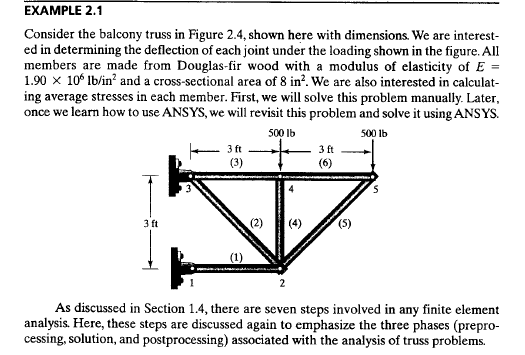
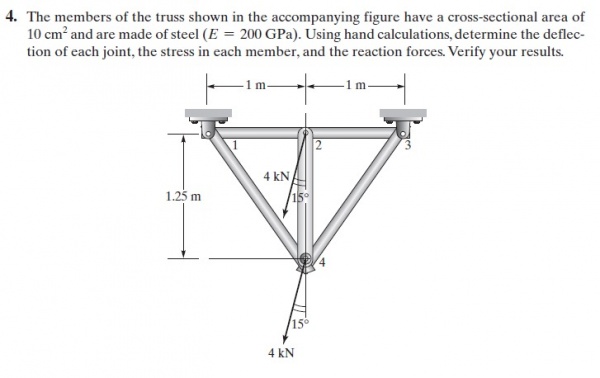
Untuk tugas dalam pertemuan III (23/11/2020) lalu, pak Dai memberi tugas untuk menyelesaikan persamaan pada soal berikut dengan menggunakan OpenModelica.
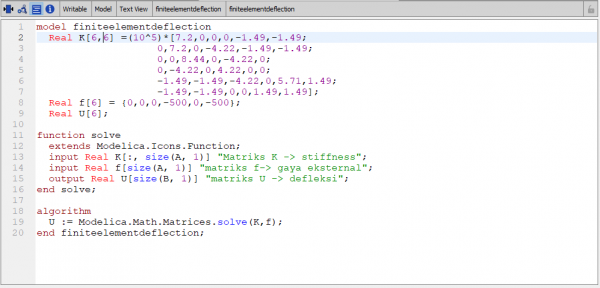
Untuk menyelesaikan defleksi pada soal tersebut, saya meng-entry coding berikut pada software OpenModelica.
dan setelah melakukan simulasi, didapatkan hasil sebagai berikut, yang mana hasil ini sama dengan yang tertera pada buku.
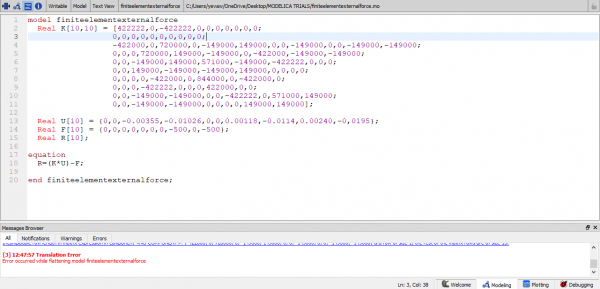
Namun, saat saya mengentry coding untuk external force, terdapat error pada saat saya akan melakukan simulasi. Saya masih berusaha melokasikan dimana titik errornya.
berikut adalah coding external force yang dinyatakan error oleh OpenModelica.
QUIZ I METODE NUMERIK (30/11/2020)
Pada pertemuan IV ini, pak Dai memberikan dua soal kuis dan kami diminta untuk menuliskan flowchart pengerjaannya. Berikut adalah dua soal kuis tersebut.
dan berikut adalah flowchart pengerjaan soal kuis tersebut yang telah saya tulis. Mengingat alur pengerjaan dua soal tersebut sama, maka flowchart berikut mencakup kedua soal tersebut.
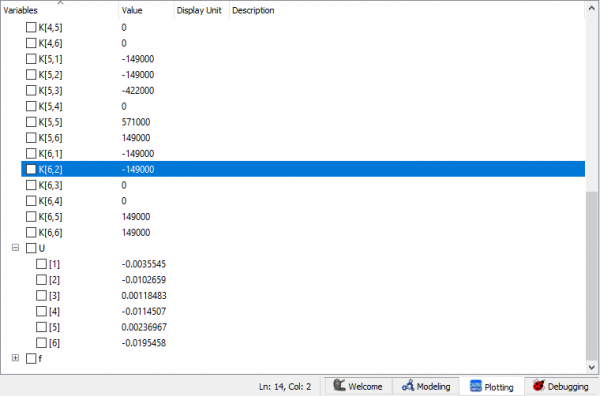
PENYELESAIAN MANUAL KUIS
|
NO 8 |
CODING
NO 4
MASTER CODE (CLASS)
|
class Quiz_no4 //establish Real parameter in order (element, i, j, theta, Area, E, length) parameter Real[:,7]inisiasi = [1, 1, 0, 10e-4, 200e9;
2, 1, 0, 10e-4, 200e9;
3, 1, -1.25, 10e-4, 200e9;
4, 0, -1.25, 10e-4, 200e9;
5, -1, -1.25, 10e-4, 200e9];
//establish nodes parameter Integer[size(inisiasi,1),2] node = [1, 2;
2, 3;
3, 4;
2, 4;
1, 4];
//number of nodes parameter Integer n=4; //xy boundary node points parameter Integer [:] Boundary_xy = {1,3}; //boundary is fixed. no change to overall truss.
//x boundary nodes parameter Integer [:] Boundary_x = {0};
//y boundary nodes parameter Integer [:] Boundary_y = {0};
//load = [F1x, F1y,....,Fnx,Fny] parameter Real [2*n] load = { 0, 0,
-1035.28, -3863.70,
0, 0,
-1035.28, -3863.70};
Real [size(inisiasi, 1)] L; Real [size(inisiasi, 1)] k; Real [size(inisiasi, 1), 4,4] Ke; Real [size(inisiasi, 1), 2*n, 2*n] Kg; Real [2*n, 2*n] KgTot; Real [2*n, 2*n] KgB; Real [2*n] U; Real [2*n] R; //check force balance Real [2] F; equation L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,3] * inisiasi[i,4] / L[i]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(n, node, Ke);
KgTot = SumStiffnessMatrixGlobal(Kg);
KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xy, Boundary_x, Boundary_y);
U = GaussJordan(KgB, load);
R = ReactionForce(KgTot, U, load);
F = CheckForce(load,R);
end Quiz_no4; |
FUNCTIONS
|
Stiffness Matrix Element function StiffnessMatrixElement input Real [:,5] inisiasi; output Real [size(inisiasi,1),4,4] Ke;
protected Real theta; Real [3] StiffTrig; Real [4,4] StiffTrans; Real [size(inisiasi,1)] k; Real [size(inisiasi,1)] L; Real float_error = 10e-10;
algorithm L := {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2)) for i in 1:size(inisiasi,1)};
k := {(inisiasi[i,3] * inisiasi[i,4] / inisiasi[i,5]) for i in 1:size(inisiasi,1)};
// Finding stiffness matrix of each element member for i in 1:size(inisiasi,1) loop
// Clearing the matrices StiffTrig := zeros(3); StiffTrans := zeros(4,4);
// Converting degrees to radians theta := Modelica.SIunits.Conversions.from_deg(inisiasi[i,2]);
// {cos^2, sin^2, sincos}
StiffTrig := {(Modelica.Math.cos(theta))^2,
(Modelica.Math.sin(theta))^2, (Modelica.Math.sin(theta)*Modelica.Math.cos(theta))};
// Handle float error elements in StiffTrig for t in 1:size(StiffTrig,1) loop if abs(StiffTrig[t]) <= float_error then StiffTrig[t] := 0; end if; end for;
// Construct stiffness transformation matrix StiffTrans := [ StiffTrig[1], StiffTrig[3], -1*StiffTrig[1], -1*StiffTrig[3]; StiffTrig[3], StiffTrig[2], -1*StiffTrig[3], -1*StiffTrig[2]; -1*StiffTrig[1], -1*StiffTrig[3], StiffTrig[1], StiffTrig[3]; -1*StiffTrig[3], -1*StiffTrig[2], StiffTrig[3], StiffTrig[2]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke for m in 1:4 loop for n in 1:4 loop Ke[i,m,n] := k[i] * StiffTrans[m,n]; end for; end for;
end for; end StiffnessMatrixElement;
|
Stiffness Matrix Global
input Integer x; input Integer [:,2] n; input Real [:,4,4] Ke; output Real [size(Ke,1),2*x,2*x] Kg; algorithm Kg := zeros(size(Ke,1),2*x,2*x);
for i in 1:size(Ke,1) loop Kg[i,2*n[i,1],2*n[i,1]]:=Ke[i,2,2]; Kg[i,2*n[i,1]-1,2*n[i,1]-1]:=Ke[i,1,1]; Kg[i,2*n[i,1],2*n[i,1]-1]:=Ke[i,2,1]; Kg[i,2*n[i,1]-1,2*n[i,1]]:=Ke[i,1,2];
Kg[i,2*n[i,2],2*n[i,2]]:=Ke[i,4,4]; Kg[i,2*n[i,2]-1,2*n[i,2]-1]:=Ke[i,3,3]; Kg[i,2*n[i,2],2*n[i,2]-1]:=Ke[i,4,3]; Kg[i,2*n[i,2]-1,2*n[i,2]]:=Ke[i,3,4];
Kg[i,2*n[i,2],2*n[i,1]]:=Ke[i,4,2]; Kg[i,2*n[i,2]-1,2*n[i,1]-1]:=Ke[i,3,1]; Kg[i,2*n[i,2],2*n[i,1]-1]:=Ke[i,4,1]; Kg[i,2*n[i,2]-1,2*n[i,1]]:=Ke[i,3,2];
Kg[i,2*n[i,1],2*n[i,2]]:=Ke[i,2,4]; Kg[i,2*n[i,1]-1,2*n[i,2]-1]:=Ke[i,1,3]; Kg[i,2*n[i,1],2*n[i,2]-1]:=Ke[i,2,3]; Kg[i,2*n[i,1]-1,2*n[i,2]]:=Ke[i,1,4]; end for; end StiffnessMatrixGlobal; |
Sum Stiffness Matrix Global function SumStiffnessMatrixGlobal input Real [:,:,:] Kg; output Real [size(Kg,2),size(Kg,2)] KgTot; algorithm for a in 1:size(Kg,2) loop
for b in 1:size(Kg,2) loop
KgTot[a,b] := sum(Kg [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal; |
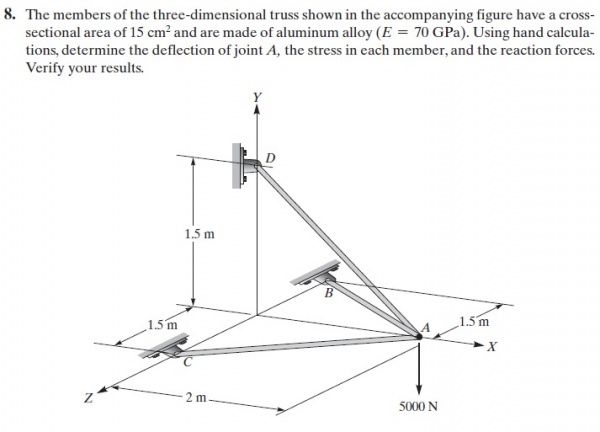
NO 8
MASTER CODE (CLASS)
|
class Quiz8 //inisiasi = [ elemen#, dX, dY, dZ, A, E]
parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //isi sesuai data
2, 0, 0, -6, 1.56, 10.6e6;
3, 0, 6, -3, 1.56, 10.6e6;
4, -6, 0, -3, 1.56, 10.6e6;
5, -6, 6, 0, 1.56, 10.6e6;
6, 0, 6, 3, 1.56, 10.6e6];
//node = [ i, j]
parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
1, 3;
1, 4;
2, 3;
2, 4;
3, 4];
//jumlah node parameter Integer n = 4; //isi sesuai data //titik node boundary xyz
parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data
//titik node boundary xy
parameter Integer [:] Boundary_xy = {4}; //isi sesuai data
//titik node boundary xz
parameter Integer [:] Boundary_xz = {0}; //isi sesuai data
//titik node boundary yz
parameter Integer [:] Boundary_yz = {0}; //isi sesuai data
//titik node boundary x
parameter Integer [:] Boundary_x = {3}; //isi sesuai data
//titik node boundary y
parameter Integer [:] Boundary_y = {0}; //isi sesuai data
//titik node boundary z
parameter Integer [:] Boundary_z = {0}; //isi sesuai data
//load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
parameter Real [3*n] load = {0, 0, 0, //isi sesuai data
0, -200, 0,
0, 0, 0,
0, 0, 0};
Real [size(inisiasi,1)] L; Real [size(inisiasi,1)] k; Real [size(inisiasi,1),6,6] Ke; Real [size(inisiasi,1),3*n,3*n] Kg; Real [3*n,3*n] KgTot; Real [3*n,3*n] KgB; Real [3*n] U; Real [3*n] R; //check force Real [3] F; equation L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi); Kg = StiffnessMatrixGlobal(n, node, Ke); KgTot = SumStiffnessMatrixGlobal(Kg); KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z); U = GaussJordan(KgB, load); R = ReactionForce(KgTot, U, load); F = CheckForce(load,R); end Quiz8; |
TUGAS PERTEMUAN V
|
Calculate Length and Cosine class Length_Cos parameter Integer Points=4; parameter Integer Trusses=6; parameter Integer C[Trusses,2]=[1,2; 1,3;
1,4;
2,3;
3,4;
2,4];
parameter Integer P[:,3]=[0,0,3; 6,0,0;
0,0,-3;
0,6,0];
//Element 1,4,5 Real L1 [size(P,1)-1]; Real cosx1 [size(P,1)-1]; Real cosy1 [size(P,1)-1]; Real cosz1 [size(P,1)-1]; //Element 2 6 Real L2 [size(P,1)-2]; Real cosx2 [size(P,1)-2]; Real cosy2 [size(P,1)-2]; Real cosz2 [size(P,1)-2]; //Element 3 Real L3 [size(P,1)-3]; Real cosx3 [size(P,1)-3]; Real cosy3 [size(P,1)-3]; Real cosz3 [size(P,1)-3]; equation //Element 1 4 5
for i in 1:1:(size(P,1)-1) loop
L1[i] = sqrt((P[i+1,1]-P[i,1]^2+(P[i+1,2]-P[i,2])^2+(P[i+1,3]-P[i,3])^2));
end for;
for i in 1:(size(P,1)-1) loop
cosx1 [i] = (P[i+1,1]-P[i,1])/L1[i];
cosy1 [i] = (P[i+1,2]-P[i,2])/L1[i];
cosz1 [i] = (P[i+1,3]-P[i,3])/L1[i];
end for;
//Element 2 6
for i in 1:1:(size(P,1)-2) loop
L2 [i] = sqrt((P[i+2,1]-P[i,1]^2+(P[i+2,2]-P[i,2])^2+(P[i+2,3]-P[i,3])^2));
end for;
for i in i:(size(P,1)-2) loop
cosx2 [i] = (P[i+2,1]-P[i,1])/L2[i];
cosy2 [i] = (P[i+2,2]-P[i,2])/L2[i];
cosz2 [i] = (P[i+2,3]-P[i,3])/L2[i];
end for;
//Element 3
for i in 1:1:(size(P,1)-3) loop
L3 [i] = sqrt((P[i+3,1]-P[i,1]^2+(P[i+3,2]-P[i,2])^2+(P[i+3,3]-P[i,3])^2));
end for;
for i in i:(size(P,1)-3) loop
cosx3 [i] = (P[i+3,1]-P[i,1])/L3[i];
cosy3 [i] = (P[i+3,2]-P[i,2])/L3[i];
cosz3 [i] = (P[i+3,3]-P[i,3])/L3[i];
end for;
end Length_Cos; |
MASTER CODE (CLASS)
| style='border-style: none none solid solid;'
class Soal5 //inisiasi = [ elemen#, dX, dY, dZ, A, E]
parameter Real [:,6] inisiasi = [1, 0.8944, 0.0000, -0.4472, 1.56, 10.6e6; //isi sesuai data
2, 0.0000, 0.0000, -1.0000, 1.56, 10.6e6;
3, 0.0000, 0.8944, -0.4472, 1.56, 10.6e6;
4, -0.8944, 0.0000, -0.4472, 1.56, 10.6e6;
5, -0.7071, 0.7071, 0.0000, 1.56, 10.6e6;
6, 0.0000, 0.8944, 0.4472, 1.56, 10.6e6];
//node = [ i, j]
parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
1, 3;
1, 4;
2, 3;
2, 4;
3, 4];
//jumlah node parameter Integer n = 4; //isi sesuai data //titik node boundary xyz
parameter Integer [:] Boundary_xyz = {1,3,4}; //isi sesuai data
//titik node boundary xy
parameter Integer [:] Boundary_xy = {3}; //isi sesuai data
//titik node boundary xz
parameter Integer [:] Boundary_xz = {0}; //isi sesuai data
//titik node boundary yz
parameter Integer [:] Boundary_yz = {0}; //isi sesuai data
//titik node boundary x
parameter Integer [:] Boundary_x = {2}; //isi sesuai data
//titik node boundary y
parameter Integer [:] Boundary_y = {4}; //isi sesuai data
//titik node boundary z
parameter Integer [:] Boundary_z = {1}; //isi sesuai data
//load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
parameter Real [3*n] load = {0, 0, 0, //isi sesuai data
0, -200, 0,
0, 0, 0,
0, 0, 0};
Real [size(inisiasi,1)] L; Real [size(inisiasi,1)] k; Real [size(inisiasi,1),6,6] Ke; Real [size(inisiasi,1),3*n,3*n] Kg; Real [3*n,3*n] KgTot; Real [3*n,3*n] KgB; Real [3*n] U; Real [3*n] R; //check force Real [3] F; equation L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi); Kg = StiffnessMatrixGlobal(n, node, Ke); KgTot = SumStiffnessMatrixGlobal(Kg); KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z); U = GaussJordan(KgB, load); R = ReactionForce(KgTot, U, load); F = CheckForce(load,R);
|