Yogi Gunawan Atmawijaya

Biodata

Yogi Gunawan Atmawijaya

Nama  : Yogi Gunawan Atmawijaya

NPM  : 1806201005

TTL  : 27 Maret 2000

Tempat Tinggal : Tangerang

Saya adalah mahasiswa FTUI angkatan 2018 jurusan Teknik Mesin.

Saya memilih jurusan teknik mesin karena setelah melihat pelajaran-pelajaran di jurusan ini cocok dengan minat saya dan saya yakin saya bisa kuliah dengan baik di Teknik Mesin

Metode Numerik

Pelajaran yang sudah saya pelajari di setengah semester pertama pada mata kuliah metode numerik yang diajar oleh Dr. Ir. Engkos Achmad Kosasih M.T. adalah :

• macam-macam error
• turunan numerik
• metode bisection
• metode newton-raphson
• metode secant
• deret mc laurint.

Minggu 1 (Rabu, 11 November 2020)

Ada 4 tujuan metode numerik

• 1. memahami konsep dengan dengan baik tentang dasar-dasar metode numerik. bila dasarnya tidak paham konsep dengan baik, maka tidak akan mengerti.
• 2. mampu menerapkan pemahaman konsep tersebut didalam permodelan numerik
• 3. mampu menerapkan metode numerik dipersoalan keteknikan
• 4. untuk mendapat nilai tambah membuat kita menajadi manusia yang beradab

Pada diskusi hari ini, Rabu, 11 Nov 2020, saya mempelejari bahwa komputer walaupun bisa memudahkan pekerjaan kita tetapi komputer juga mempunyai keterbatasan. Jadi sejatinya kita tidak dapat mengandalkan komputer sepenuhnya. Dan sebagai manusia kita juga tidak luput dari ketidaktahuan karena sejatinya hanya Tuhan yang Maha Tahu

Tugas 1

Untuk tugas minggu 1 kami diminta untuk melihat tutorial Open Modelica dari youtube. Setelah melihat tutorial tersebut kami membuat video tutorial singkat. Berikut ini adalah video tutorial OpenModelica Basic

Minggu 2 (Rabu, 18 November 2020)

Sebelum dijelaskan materi, kami diminta mereview hal-hal apa saja yang sudah kami pelajari diminggu 1 dan apa saja hal yang sudah dicoba untuk tugas 1 yaitu memepelajari dasar dari Open Modelica. Pak Dai menjelaskan kenapa Pak Dai memilih aplikasi open modelica dibandingkan program lain untuk tools belajar kami. Pak Dai menjelaskan bahwa aplikasi Open Modelica ini sebenarnya bukan aplikasi programing, melainkan aplikasi untuk modelling. Open Modelica tidak mempunyai bahasa program sendiri, itu kenapa proses dari simulasi Open Modelica ini lebih lama dibandingkan aplikasi lain. Open modelica memproses data lebih lama dikarenakan Open Modelica harus menerjemahkan perintah yang kita tulis menjadi bahasa C++, setelah itu baru data bisa diproses.

Setelah itu kami diminta mencoba membuat suatu file class yang digunakan untuk "memanggil" suatu fungsi dari file function. Kami membuat file function sebagai berikut :

FungsiTambahX1.mo

function FungsiTambahX1

input Real x;
output Real y;

algorithm
y:=x+10;

end FungsiTambahX1;

Setelah itu kami membuat file class untuk "memanggil" fungsi dari file function diatas. Pseudocodenya sebagai berikut :

Panggil.mo

class Panggil

parameter Real x1=5;
Real hasil10tambahx1;

equation
hasil10tambahx1=FungsiTambahX1(x1);

end Panggil;

Dijelaskan dengan memanggil file function diatas, maka pada saat di file class, inputnya menjadi x1 dimana x1 tersebut mempunyai nilai dan nilai tersebut akan menjadi input dari persamaan yang masukan di file FungsiTambahX1.mo

Tugas 2

Untuk tugas 2, kami diminta untuk membuat suatu fungsi panggil seperti yang dicontohkan pada saat kelas menggunakan persamaan aljabar simultan dan variable array. Persamaan Aljabar Simultan sendiri adalah persamaan yang kompleks karena memiliki banyak variable yang perlu dicari nilainya. Variable array adalah variable yang didalamnya memiliki beberapa data nilai. Pada tugas ini saya mencoba membuatnya menggunakan 3 persamaan sederhana yang memiliki 3 variable yang harus dicari nilainya. persamaannya adalah sebagai berikut :

Lalu saya buat file function sebagai berikut :

Gauss_Function.mo

function Gauss_Function

input Real P[3,3];
input Real Q[3];
output Real R[3];

algorithm

R:=Modelica.Math.Matrices.solve(P,Q);

end Gauss_Function;

Dan saya membuat file class sebagai berikut :

Gauss_Class.mo

class Gauss_Class

parameter Real A[3,3]=[2,5,3;3,4,2;1,3,1];
parameter Real B[3]={1,-3,2};
Real X[3];

equation

X=Gauss_Function(A,B);

end Gauss_Class;

Berikut adalah video penjelasan tentang pembuatan 2 file diatas :

Minggu 3 (Rabu, 25 November 2020)

Pada minggu ketiga, kami dijelaskan tentang pseudocode gauss elimination secara manual. Pak Dai menginginkan kami bisa membuat pseudocode sendiri tanpa menggunakan fungsi yang sudah disediakan dari OpenModelica itu sendiri. Jadi pada saat dikelas kami dijelaskan oleh Christo. Christo adalah salah satu mahasiswa yang juga mengambil mata kuliah metode numerik yang diajar oleh pak Dai. Christo menjelaskan dengan sangat jelas psudocode untuk gauss. Pseudocode dari gauss jordan berdasarkan apa yang sudah Christo jelaskan adalah sebagai berikut :

GaussJordan.mo

function GaussJordan

input Real [:,:] A;
output Real [:,:] B;

protected // untuk local variable
Integer h = 1;    //pivot row
Integer k = 1;    //pivot coloumn
Integer m = size(A,1); //Number of row
Integer n = size(A,2); //Number of column
Integer c = 0;
Integer max_row; // Row index of max number in pivot column

Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;

Real float_error = 10e-10;


algorithm

//fungsi input A dan output B 
B := A;
  
while h <= m and k <= n loop

  for i in 1 : m loop
    for j in 1 : n loop
     if abs(B[i,j]) <= float_error then
       B[i,j] := 0;
      end if;
    end for;
  end for;

//Finding pivot 
  pivot_column:= {B[i,h] for i in h:m};
  
    //Mencari baris terbawah yang mempunyai nilai pivot tertinggi
    c:=h-1;
    for element in pivot_column loop
      c:= c+1;
      if abs(element)== max(abs(pivot_column)) then
        max_row :=c;
      end if;
    end for;
    
  //Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
  if B[max_row,k] == 0 then
    k:=k+1;
   
  else 
    // tukar row h - max_row
    temp_array := B;
    temp_array[h] := B[max_row];
    temp_array[max_row] := B[h];
    B:= temp_array;
    
    //devide pivot row by pivot number
     B[h] := B[h]/B[h,k];
     
     for i in (h+1) :m loop
       r := B[i,k]/B[h,k];
      
      B[i,k]:=0;
      
      for j in (k+1) : n loop
        B[i,j] := B[i,j]-B[h,j] * r;
      end for;
    end for;
    
    //move ke pivot kolom dan row selanjutnya
    h := h+1;
    k := k+1;
    
  end if;
  
end while;

// proses dari kanan atas
h :=m;
k :=n;

while h >=1 and k>=1 loop
  
  //dealing with error
  for i in 1:m loop
    for j in 1:n loop
      if abs(B[i,j]) <=float_error then
        B[i,j]:=0;
      end if;
    end for;
  end for; 

//finding pivot 
    pivot_row := {B[h,i] for i in 1:k};
    
    //Get position index k of pivot 
    c := 0;
    for element in pivot_row loop
      c := c+1;
      if element <> 0 then
        break;
      end if;
    end for;
    k:= c;
    
  // no pivot in this row, move to next row
  if B[h,k] == 0 then 
    h:= h-1;
    
  else
    //perform row operatation
    for i in 1:(h-1) loop
      r := B[i,k];
      B[i] := B[i] - B[h] *r;
    end for;
    
    //move to next pivot row dan column
    h:=h+1;
    k:=k+1;
    
  end if;
  
end while;
    
     
end GaussJordan;

Lalu kami diminta untuk membuat pseudocode open modelica dari suatu pseudocode matlab yang ada dibuku yaitu Fig. 9.4 :

Pseudocodenya adalah sebagai berikut :

NaiveGauss.mo

function NaiveGauss

input Real [3,3] A; 
input Real [3] B;   
output Real [3] x;  

protected
Real [3,3] a;
Real [3] b;
Integer m = size(A,1); // kolom 
Integer n = size(A,2); // baris
Real k = 1;      
Real i = 1;       
Real j = 1;       
Real factor = 1; 
Real sum = 1;     
algorithm

// Transfer input matrix (A,B) into variables (a,b)
a := A;
b := B;

// Forward Elimination
for k in 1:(n-1) loop
  for i in (k+1):n loop
    factor := a[i,k] / a[k,k];
    for j in (k+1):n loop
      a[i,j] := a[i,j] - (factor * a[k,j]);
    end for;
    b[i] := b[i] - (factor * b[k]);
  end for;
end for;

// Back Substitution
x[n] := b[n] / a[n,n];
for i in (n-1):(-1) loop
  sum := b[i];
  for j in (i+1):n loop
    sum := sum - (a[i,j] * x[j]);
  end for;
  x[i] := sum / a[i,i];
end for;

end NaiveGauss;

Lalu pseudocode tersebut digunakan untuk menyelesaikan persamaan example 9.5 dan penyelesaiannya adalah sebagai berikut :

Ex9_5.mo

class Ex9_5

parameter Real A[3,3]=[3,-0.1,-0.2;
                       0.1,7,-0.3;
                       0.3,-0.2,10];
parameter Real B[3]={7.85,-19.3,71.4};
Real x[3];

equation
x=NaiveGauss(A,B);       
                       

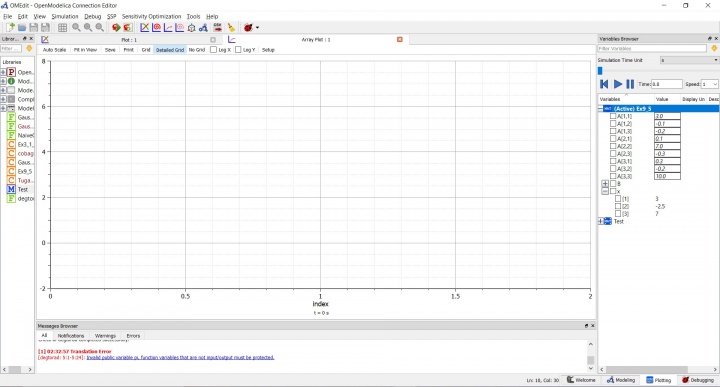
end Ex9_5;

Dari class tersebut disimulate dan didapatkan hasil sebagai berikut :