Difference between revisions of "Metnum03 - Gema Akbar Ilhamsyah"
(→Pertemuan II) |
(→Tugas 2 =Penyelesaian persamaan aljabar simultan) |
||
| Line 101: | Line 101: | ||
[[File:Aaa2.png|600px|center]] | [[File:Aaa2.png|600px|center]] | ||
| + | |||
| + | Saya mendapat penyelesaian persamaan diatas adalah: X1=3.5 , X2=0.75 , X3=0.75 | ||
Revision as of 10:17, 30 November 2020
BIODATA DIRI
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Nama: Gema Akbar Ilhamsyah
NPM : 1806233386
Fakultas/Jurusan: Teknik/ Teknik Mesin
Tempat dan Tanggal lahir: Jakarta,7 Januari 2000
Contents
Pertemuan I
-Pemahaman Materi Sebelum UTS
Penjelasan Metode Numerik itu sendiri adalah teknik penyelesaian masalah dengan menggunakan operasi hitungan tambah, kurang, kali, bagi. Metode ini digunakan untuk membantu matematis untuk menyelesaikan permasalahan yang tidak dapat diselesaikan dengan metode analitik ataupun permasalahan yang sangat sulit dan memeakan banyak waktu untuk diselesaikan dengan metode analitik. Pada kesempatan kali ini saya akan mencoba menjabarkan apa saja materi mata kuliah yang dipelajari sebelum UTS, yaitu;
1. mencari akar akar persamaan non linear
Penyelesaian untuk mencari akar-akar persamaan non linear ada beberapa cara yaitu:
a)Metode Tertutup: Metode yang termasuk ke dalam golongan ini mencari akar di dalam selang [a,b]. Selang [a,b] sudah dipastikan berisi minimal satu buah akar, karena itu metode jenis ini selalu berhasil menemukan akar. Dengan kata lain, lelarannya selalu konvergen (menuju) ke akar, karena itu metode tertutup kadang-kadang dinamakan juga metode konvergen. b)Metode Terbuka: Yang diperlukan pada metode ini, adalah tebakan awal akar, lalu dengan prosedur lelaran, kita menggunakannya untuk menghitung hampiran akar yang baru. Pada setiap lelaran, hampiran akar lama yang dipakai untuk menghitung hampiran akar yang baru. Mungkin saja hampiran akar yang baru mendekati akar sejati (konvergen), atau mungkin menjauhinya (divergen). Karena itu, metode terbuka tidak selalu berhasil menemukan akar, kadang-kadang konvergen, kadangkala ia divergen.
2. turunan numerik
Untuk Penurunan Numerik, terdapat 3 metode, yaitu:
a)Forward difference aproximation
b)Backward difference aproximation
c)Central difference aproximation
3. regresi
Regresi merupakan alat ukur yg digunakan untuk mengetahui ada tidaknya korelasi antarvariabel. Analisis regresi lebih akurat dlm analisis korelasi karena tingkat perubahan suatu variabel terhdp variabel lainnya dpt ditentukan). Jadi pada regresi, peramalan atau perkiraan nilai variabel terikat pada nilai variabel bebas lebih akurat pula.
Regresi linier adalah regresi yang variabel bebasnya (variabel X) berpangkat paling tinggi satu. Utk regresi sederhana, yaitu regresi linier yg hanya melibatkan dua variabel (variabel X dan Y).
Y=a+bX
4. interpolasi
Pertemuan II
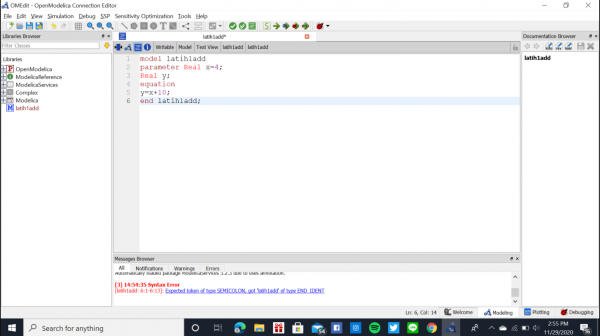
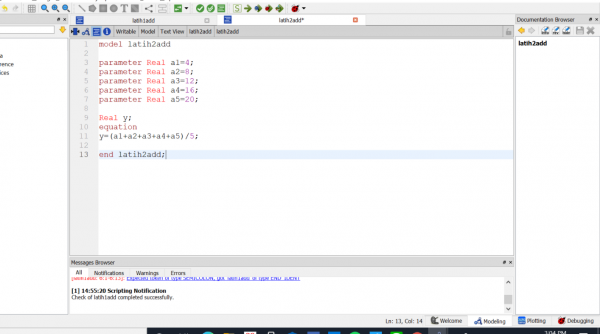
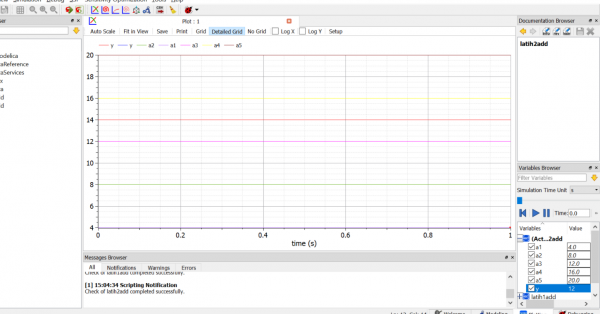
Pada pertemuan kali ini kami melakukan diskusi tentang software OpenModelica dengan Pak Dai. Lalu kami diberikan latihan untuk membuat perhitungan sederhana dengan software Open Modelica, yaitu menjumlahkan angka 10 dengan suatu variabel serta mencari rata-rata data yang didapat.
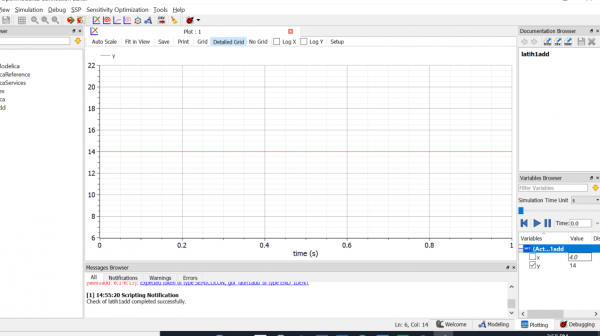
Saya Melakukan Perhitungan rumus y=x+10 dengan x=4
dan saya mendapat y=14
Tugas 2 =Penyelesaian persamaan aljabar simultan
Aljabar Simultan adalah suatu penyelesaian matematik yang kompleks sehingga membutuhkan penyederhanaan dengan menggunakan bantuan software yang sudah disediakan seperti OpenModelica. Ada beberapa metode yang bisa digunakan pada Aljabar Simultan:
1. Metode Eliminasi Gauss
2. Metode Crammer
3. Metode Gauss Seidel
4. Metode Gauss-Jordan
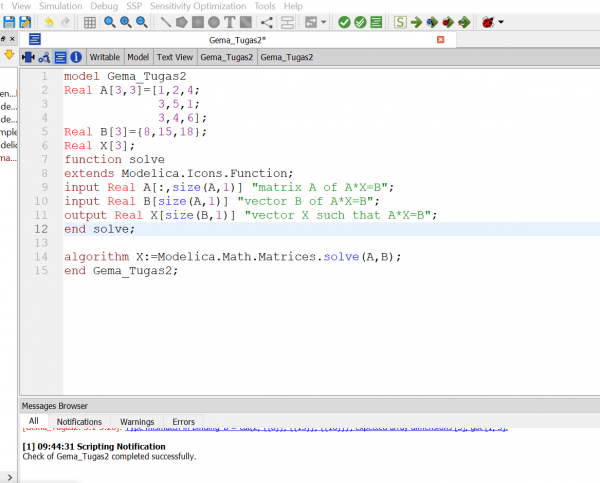
Untuk tugas 2 ini saya menggunakan persamaan berikut:
1. X1+2X2+4X3=12
2. 3X1+5X2+X3=15
3. 3X1+4X2+6X3=18
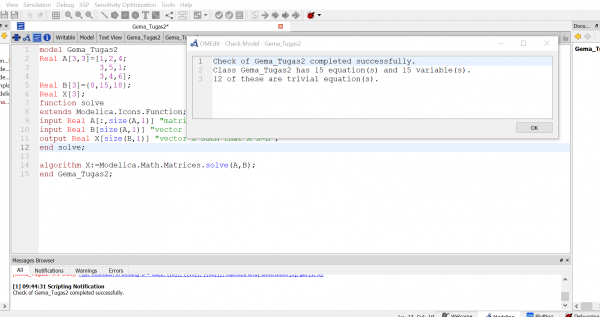
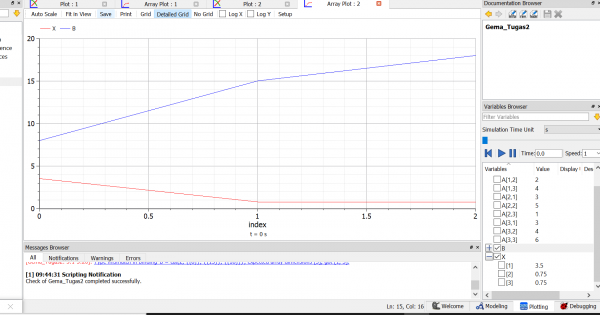
Lalu penyelesaian pada OpenModelica seperti berikut:
Saya mendapat penyelesaian persamaan diatas adalah: X1=3.5 , X2=0.75 , X3=0.75