Difference between revisions of "Metnum03-Ahmad Farras"
Ahmad Farras (talk | contribs) |
Ahmad Farras (talk | contribs) |
||
| Line 61: | Line 61: | ||
hasil X yang dihasilkan dari penyelesaian persamaan diatas ialah (1,-2,1,1) | hasil X yang dihasilkan dari penyelesaian persamaan diatas ialah (1,-2,1,1) | ||
| + | |||
| + | == Pertemuan ketiga 23 November 2020 == | ||
Revision as of 13:10, 23 November 2020
Assalamualaikum wrwb
Nama Ahmad Farras NPM 1906435435
Contents
Pertemuan pertama 9 November 2020
Disini Bapak Indra memberi tugas untuk membuat open modelica dengan materi yang sudah dipelajari sebelum UTS Berikut video yang terkait yang telah saya buat
https://www.youtube.com/watch?v=XSdRoteD3d4
Pertemuan Kedua 16 November 2020
Pada pertemua ini Bapak Indra memberi tugas untuk membuat suatu program sederhana yang dimana program tersebut di koding pada openmodelica,Berikut ialah penjelasan menggunakan openmodelica untuk mencari mean pada suatu data:
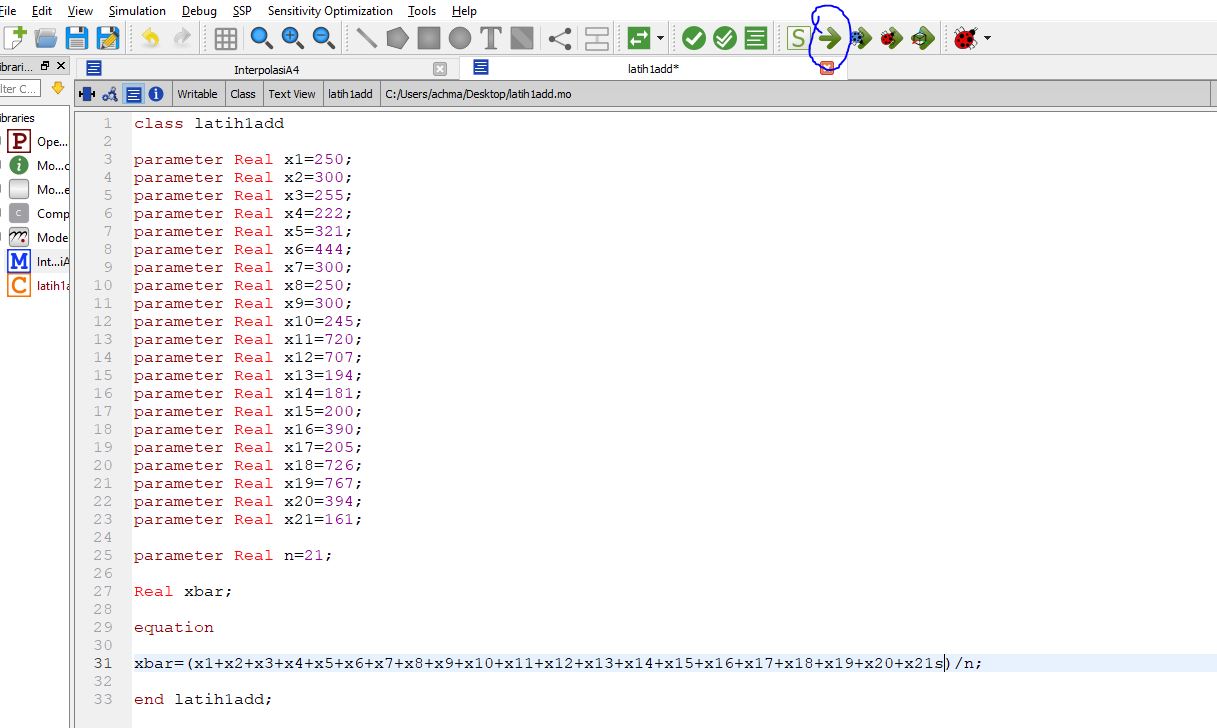
1.Menginput data,nilai yang dicari dan equation yang digunakan
Disini kita menginput data data yang dibutuhkan pada persoalan ini saya mengambil sampel 21 data.Hal tersebut kita masukan ke parameter real seperti gambar diatas.Parameter real digunakan untuk memberi informasi data yang diketahui.Setelah itu menulis "real" untuk angka yang dicari.Setelah data yang diketahui dan ditanyakan sudah dilakukan maka kita langsung menulis equation yang dimana equation pada data ini ialah
xbar=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20+x21)/n;
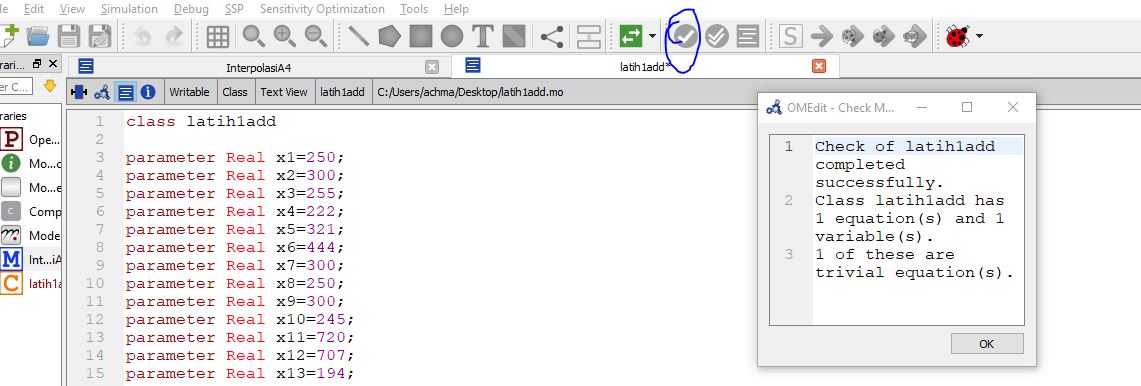
2.Mengecek dari program yang kita buat
Pada step ini kita mengecek apakah program kita apakah sudah bisa disimulasi atau tidak bisa disimulasi
3.Jika bisa maka langsung mengeklik tombol "simulate"
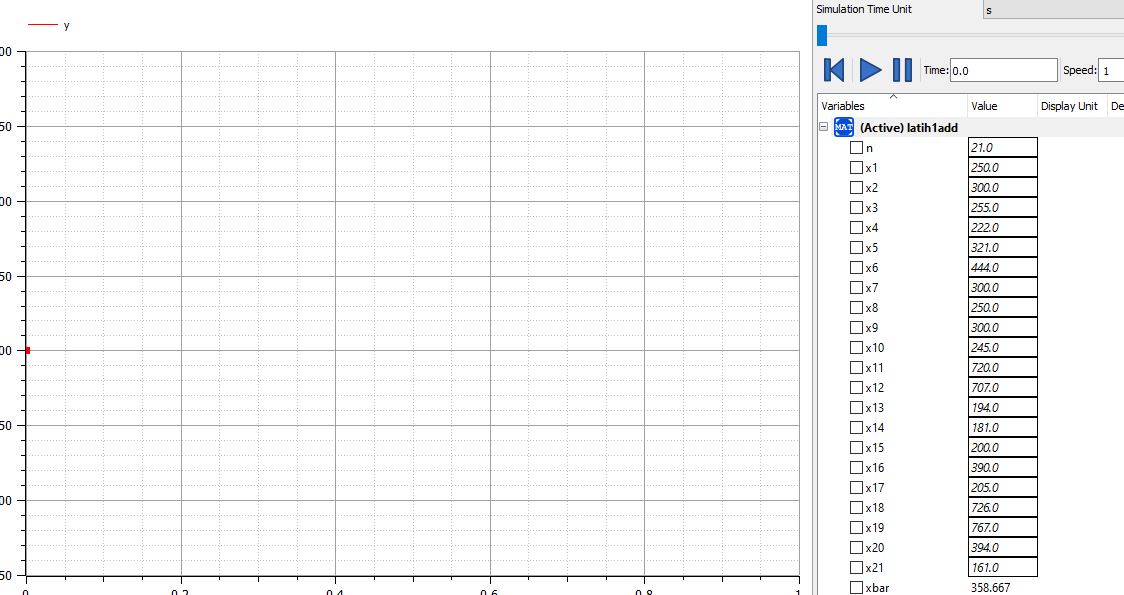
4.Berikut hasil dari nilai rata rata dari data yang saya buat
Tugas 2
Persamaan aljabar simultan tersebut dapat diselesaikan dengan matematik secara umum seperti Gauss Elimination, atau menggunakan metode lain seperti Gauss Elimination yang melibatkan matriks,atau Gauss Seidel.Pada persoalan dibawah ini saya akan menggunakan metode Gauss Elimination untuk menyelesaikan persamaan berikut.
10x1 - x2 +2x3=6
-x1+11x2-x3+3x4=25
2x1-x2+10x3-x4=-11
3x2-x3+8x4=15
Gauss Elimination adalah algoritme yang digunakan untuk menyelesaikan persamaan linear. Metode ini melibatkan perubahan bentuk sistem persamaan menjadi bentuk matriks. Setelah mengubah sistem dalam bentuk matriks,dilakukan pengurangan baris dengan mengganti posisi baris, dan/atau melakukan operasi penjumlahan dan pengurangan antar baris.
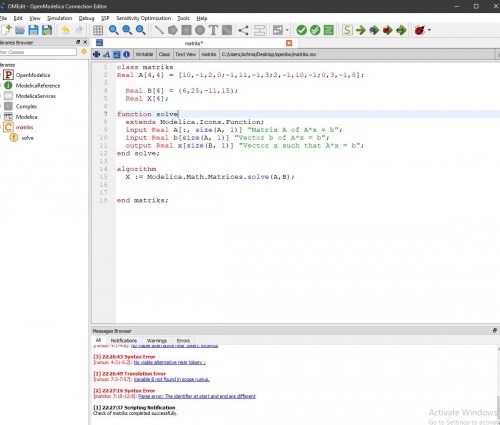
Pada aplikasi OpenModelica terdapat model untuk menyelesaikan permasalahan aljabar simultan dengan menggunakan metode Gauss Elimination.Berikut ialah model yang saya buat dengan software OpenModelica:
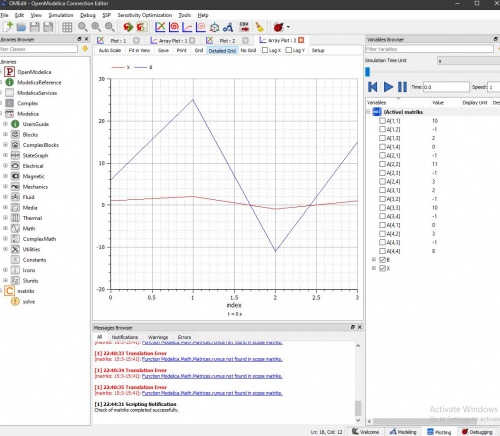
Saya menggunakan perintah yang ada di library modelica yaitu "Modelica.Math.Matrices.solve(A,b)" untuk menyelesaikan sistem persamaan linier eliminasi gauss yang ada diatas.Setelah melakukan pengecekan dan melakukan simulasi terhadap model yang telah saya buat,selanjutnya melakukan plotting terhadap hasil simulasi tersebut. Berikut adalah hasil plotting dari simulasi persamaan diatas:
hasil X yang dihasilkan dari penyelesaian persamaan diatas ialah (1,-2,1,1)