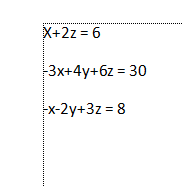Difference between revisions of "Metnum03-Trio Kurnia Ryplida"
(→Pertemuan Tanggal 16 November 2020) |
(→Pertemuan Tanggal 16 November 2020) |
||
| Line 58: | Line 58: | ||
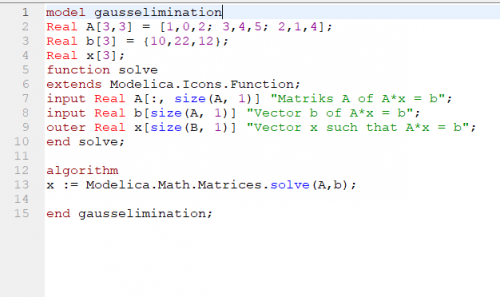
berikut bentuk penyelesaian dengan menggunakan open modelica : | berikut bentuk penyelesaian dengan menggunakan open modelica : | ||
| − | [[File:fungsimatriks.png| | + | [[File:fungsimatriks.png|500px|center]] |
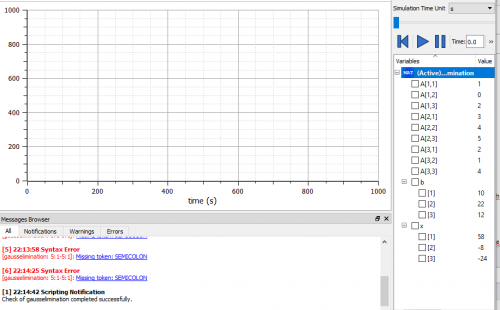
| − | [[File:hasilmatriks1.png| | + | [[File:hasilmatriks1.png|500px|center]] |
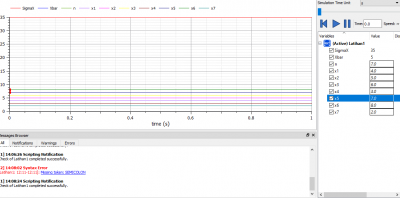
dapat dilihat bahwa hasil plotting tersebut menunjukkan penyelesaian dari permasalaha sistem persamaan yang telah ditunjukkan sebelumnya, yaitu x1=58, x2=-8, x3=-24. | dapat dilihat bahwa hasil plotting tersebut menunjukkan penyelesaian dari permasalaha sistem persamaan yang telah ditunjukkan sebelumnya, yaitu x1=58, x2=-8, x3=-24. | ||
Revision as of 22:23, 22 November 2020
Alhamdulillah, segala puji bagi Allah SWT Tuhan semesta alam dan sholawat beserta salam kepada Nabi Muhammad SAW.
BIODATA
Nama :Trio Kurnia Ryplida
Npm : 1906435561
Agama : Islam
No.Telp : 085274017943
Pendidikan Terakhir: Diploma III
Tempat/Tgl lahir : Padang, 29 oktober 1997
Pertemuan Tanggal 9 November 2020
Pada pertemuan pertama Pak Dai memberikan PR, sebagai berikut :
1. apa saja yang sudah dipelajari di metode numerik?
2. Buatlah video tentang aplikasi Open Modelica.
Numerical Differentiation
pada kasus ini menggunakan perumusan :
Untuk vido tentang aplikasi OpenModelica terdapat pada link : https://www.youtube.com/watch?v=uxVO7iPxMKo
Pertemuan Tanggal 16 November 2020
Hari ini pak Dai memberikan petunjuk bagaimana cara membuat sebuah program sederhana
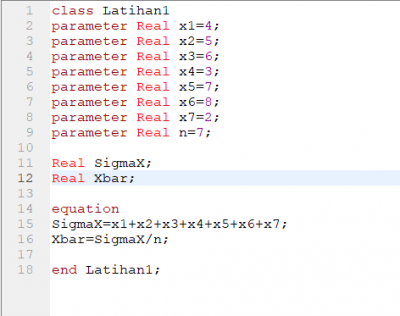
1. membuat penjumlahan angka 10
2. membuat hasil rata-rata
Pr menyelesaikan masalah 3 aljabar sebagai berikut :
persamaan ini akan diselesaikan dengan menggunakan open modelica dengan metode Gauss Elimination. Maka persamaan ini akan diubah dalam bentuk matriks.
berikut bentuk penyelesaian dengan menggunakan open modelica :
dapat dilihat bahwa hasil plotting tersebut menunjukkan penyelesaian dari permasalaha sistem persamaan yang telah ditunjukkan sebelumnya, yaitu x1=58, x2=-8, x3=-24.