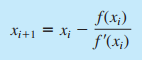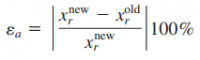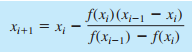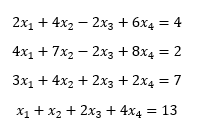Difference between revisions of "Metnum03 Ikhsanul Fikri Fakhrurrozi"
Ikhsanul ff (talk | contribs) (→Pertemuan Kedua) |
Ikhsanul ff (talk | contribs) |
||
| Line 120: | Line 120: | ||
Hasil dari gauss elimination tersebut adalah x1 = -41, x2 = 26, x3 = 12, x4 = 1. | Hasil dari gauss elimination tersebut adalah x1 = -41, x2 = 26, x3 = 12, x4 = 1. | ||
| + | |||
| + | |||
| + | |||
| + | == '''Pertemuan Ketiga''' == | ||
| + | ---- | ||
| + | '''Hari, Tanggal : Senin 23 November 2020''' | ||
| + | '''Oleh : Dr. Ahmad Indra''' | ||
Revision as of 13:27, 23 November 2020
Alhamdulillah, segala puji bagi Allah SWT dan sholawat serta salam kepada Nabi Muhammad SAW, Perkenalkan nama saya Fikri, informasi singkat saya dapat dilihat sebagai berikut :
Nama : Ikhsanul Fikri Fakhrurrozi
Email : ifikrifakhrurrozi97@gmail.com
Contents
Pertemuan Pasca UTS
Pertemuan Pertama
Hari, Tanggal : Senin 9 November 2020 Oleh : Dr. Ahmad Indra
Pada pertemuan pertama Pak Dai memberikan PR, sebagai berikut :
1. apa saja yang sudah dipelajari di metode numerik?
2. Buatlah video tentang aplikasi Open Modelica.
Metode bisection
Metode bisection merupakan salah satu metode incremental search yang mana interval dari dua titik x dibagi dua sehingga mendapatkan nilai x lagi. Berikut adalah langkah-langkah metode bisection :
• Lakukan tembakan pada dua titik terendah (xi) dan titik tertinggi (xu). • Kemudian carilah xr dengan menjumlahkan antara xi dan xu kemudian hasil dari penjumlahan tersebut dibagi dua. • Lakukan evaluasi sebagai berikut :
Jika f(xl) f(xr) < 0, akar persamaan terletak di sub interval terendah. Jadi, atur xu = xr kemudian kembali ke langkah 2.
Jika f(xl) f(xr) > 0, akar persamaan terletak di sub interval tertinggi. Jadi, atur xi = xr kemudian kembali ke langkah 2.
Jika f(xl) f(xr) = 0, akar persamaan sama dengan xr. Sehingga hentikan perhitungan.
Metode Newton-Raphson
Metode newton-raphson dapat diwakili dengan formula berikut :
Kemudian aplikasi dari metode Newton-Raphson adalah sebagai berikut :
Perhitungan nilai persentase error antara nilai akhir dan nilai awal adalah selisih antara nilai awal dan nilai akhir dibagi dengan nilai akhir kemudian hasilnya dikalikan 100 untuk mendapatkan persentase dari nilai errornya.
Metode Sekan
Metode sekan dapat diwakili dengan formula berikut :
Aplikasinya dapat dilihat pada contoh soal berikut :
Kemudian untuk aplikasi penggunaan openmodelica saya berikan penjelasannya dalam bentuk video dengan link berikut ini :
Aplikasi Least Square Fit Regression pada Openmodelica
Pertemuan Kedua
Hari, Tanggal : Senin 16 November 2020 Oleh : Dr. Ahmad Indra
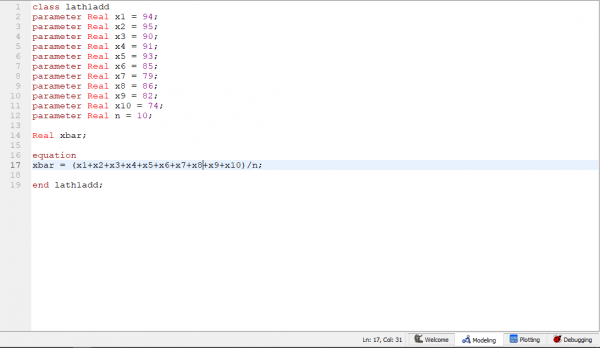
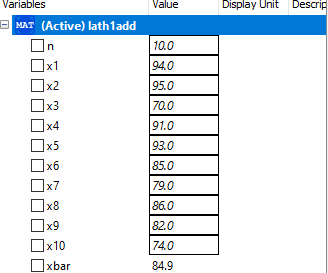
Pada pertemuan hari ini pak Dai mengevaluasi hasil belaja mahasiswa terkait dengan penggunaan aplikasi openmodelica. Kemudian mahasiswa diminta untuk membuat coding sederhana terkait nilai rata-rata 10 sample. Berikut saya lampirkan hasil coding dan simulasinya.
PR Aljabar Simultan dengan Openmodelica
Kemudian pada hari ini juga pak Dai memberikan PR kepada mahasiswa berupa aplikasi penyelesaian problem aljabar simultan baik itu menggunakan metode gauss elimination, gauss-seidell, dll. Kemudian saya menggunakan persamaan berikut ini dalam menyelesaikan problem aljabar simultan menggunakan gauss elimination :
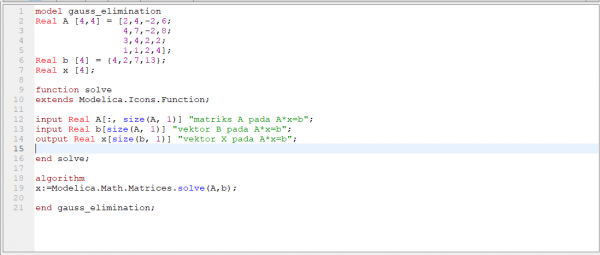
kemudian saya menyelesaikan persamaan aljabar tersebut dengan menggunakan metode gauss elimination di software openmodelica. berikut adalah hasil codingnya :
Pada coding ini saya menggunakan fasilitas library pada openmodelica yaitu "Modelica.Math.Matrices.solve(A,b)" untuk menyelesaikan problem aljabar tersebut. Kemudian hasil dari coding tersebut adalah sebagai berikut :
Hasil dari gauss elimination tersebut adalah x1 = -41, x2 = 26, x3 = 12, x4 = 1.
Pertemuan Ketiga
Hari, Tanggal : Senin 23 November 2020 Oleh : Dr. Ahmad Indra