Difference between revisions of "Metnum03-Samuel Sitompul"
(Created page with "=Pertemuan Kedua Metode Numerik 03= Pada pertemuan kedua kali ini, Kami diminta oleh Pak Dai untuk menunjukkan pemahaman kami mengenai tugas minggu lalu, yaitu mempelajari Op...") |
|||
| Line 1: | Line 1: | ||
| − | =Pertemuan Kedua Metode Numerik 03= | + | == Biodata == |
| + | |||
| + | Nama: Samuel Albert B C H Sitompul | ||
| + | |||
| + | NPM : 1606907556 | ||
| + | |||
| + | Hobi: Membaca Buku | ||
| + | |||
| + | == Pertemuan Pertama Metode Numerik 03 == | ||
| + | |||
| + | |||
| + | |||
| + | == Pertemuan Kedua Metode Numerik 03 == | ||
Pada pertemuan kedua kali ini, Kami diminta oleh Pak Dai untuk menunjukkan pemahaman kami mengenai tugas minggu lalu, yaitu mempelajari OpenModelica. Lalu kami melakukan simulasi dengan membuat program sederhana didalam OpenModelica untuk menjumlahkan 10 angka pada variabel. | Pada pertemuan kedua kali ini, Kami diminta oleh Pak Dai untuk menunjukkan pemahaman kami mengenai tugas minggu lalu, yaitu mempelajari OpenModelica. Lalu kami melakukan simulasi dengan membuat program sederhana didalam OpenModelica untuk menjumlahkan 10 angka pada variabel. | ||
| Line 16: | Line 28: | ||
dapat dilihat bahwa tiap garis menunjukkan penyelesaian dari sistem persamaan tersebut. Terdapat 5 solusi dari 5 sistem persamaan dengan 5 variabel | dapat dilihat bahwa tiap garis menunjukkan penyelesaian dari sistem persamaan tersebut. Terdapat 5 solusi dari 5 sistem persamaan dengan 5 variabel | ||
| + | |||
| + | == Pertemuan Ketiga Metode Numerik 03 == | ||
Revision as of 13:52, 23 November 2020
Contents
Biodata
Nama: Samuel Albert B C H Sitompul
NPM : 1606907556
Hobi: Membaca Buku
Pertemuan Pertama Metode Numerik 03
Pertemuan Kedua Metode Numerik 03
Pada pertemuan kedua kali ini, Kami diminta oleh Pak Dai untuk menunjukkan pemahaman kami mengenai tugas minggu lalu, yaitu mempelajari OpenModelica. Lalu kami melakukan simulasi dengan membuat program sederhana didalam OpenModelica untuk menjumlahkan 10 angka pada variabel.
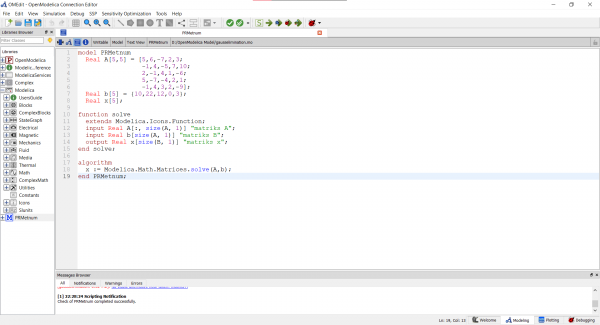
Setelah kelas, Pak Dai memberikan tugas kepada kita untuk membuat simulasi untuk menyelesaikan persamaan aljabar simultan (bisa metode eliminasi gauss, metode gauss seidel, dsb.) Berikut adalah hasil percobaan saya untuk menyelesaikan sistem persamaan aljabar. Untuk simulasi ini, saya menggunakan metode eliminasi gauss untuk menyelesaikan permasalahan aljabar simultan.
Metode eliminasi gauss merupakan salah satu metode dalam menyelesaikan sebuah sistem persamaan dengan mengubah sistem persamaan tersebut kedalam bentuk matrix. Setelah diubah, lalu matrix yang berisi angka dipindah-ruaskan lalu diselesaikan sehingga didapat nilai-nilai dari variabel yang kita cari.
Berikut adalah model simulasi yang saya buat:
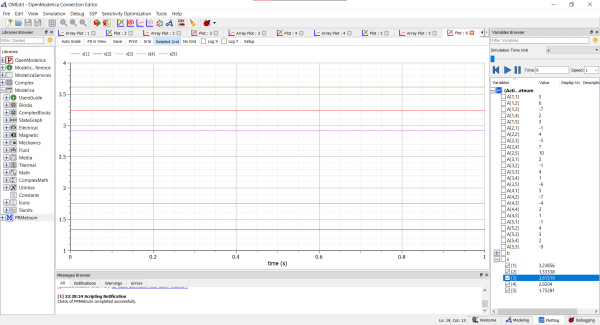
Saya mencoba menyelesaikan 5 sistem persamaan linier dengan metode eliminasi gauss dengan perintah "Modelica.Math.Matrices.solve(A,b)". Setelah melakukan pengecekan model, saya menjalankan simulasi dan melakukan plotting seusai simulasi. Berikut adalah hasil plotting tersebut:
dapat dilihat bahwa tiap garis menunjukkan penyelesaian dari sistem persamaan tersebut. Terdapat 5 solusi dari 5 sistem persamaan dengan 5 variabel