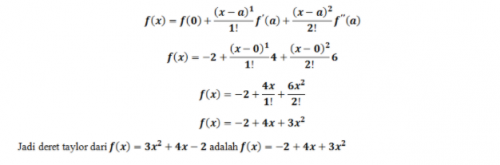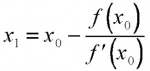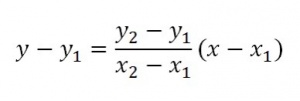Difference between revisions of "Metnum03 Luthfi Aldianta"
| Line 110: | Line 110: | ||
Dengan menggunakan persamaan, | Dengan menggunakan persamaan, | ||
| − | + | X1 + 2X2 + X3 = 2 | |
| − | + | 3X1 + X2 + 3x3 = 5 | |
| − | + | 2X1 - X2 + x3 = 4 | |
Didapatkan percobaan sebagai berikut. | Didapatkan percobaan sebagai berikut. | ||
| + | |||
| + | |||
| + | |||
| + | [[File:Luthfi 1 simulasi.png|450px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | [[File:Luthfi 2 simulasi.png|450px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | [[File:Luthfi 3 simulasi.png|450px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | [[File:Luthfi 4 simulasi.png|450px|center]] | ||
Revision as of 12:25, 22 November 2020
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
Contents
BIODATA DIRI
Nama : Luthfi Aldianta
NPM : 1806181804
Program studi : Teknik Mesin
Tempat Tanggal Lahir : Medan 22 April 2000
Pertemuan Metode Numerik 1 : 9 November 2020
Assalamualaikum Wr. Wb. Pada pertemuan hari ini Pak Dai memberikan arahan dalam sistem pembelajaran menggunakan tools Air.eng.ui.ac.id sebagai media belajar. Kemudian Pak Dai memberikan gambaran mengenai 4 poin penting dalam berlangsungnya kegiatan belajar khususnya mata kuliah metode numerik. Pertama adalah memahami kembali konsep - konsep metode numerik yang telah dipelajari di perkuliahan sebelum UTS, dimana outuputnya dapat dituliskan kembali di page masing - masing mahasiswa dan sebagai pengingat kembali materi tersebut. Kedua yaitu dari materi yang telah dipelajari kembali, dapat melakukan pengerjaan soal - soal atau perhitungan - perhitungan untuk lebih menguasai konsep materi. Ketiga adalah mengaplikasikan metode numerik pada persoalan - persoalan yang berkaitan dengan teknik mesin sebagai outputnya. Dan terakhir yaitu, nilai tambah bagi diri sendiri, dimana sebagai tolak ukur sudah sejauh apa menguasai materi metode numerik dan peningkatan pengetahuan yang telah dikuasai.
Materi Metode Numerik : Sebelum UTS
Berdasarkan pemahaman yang penulis dapat dari perkuliahan sebelum UTS yaitu mengenai deret Mclaurin dan deret Taylor, deret Mclaurin sendiri adalah fungsi f(x) yang memiliki turunan f'(x), f"(x), f"'(x), dan seterusnya yang kontinu. Kemudian diekpansi kedalam deret Taylor. Deret Taylor ini yang akan menghasilkan nilai dari turunan berdasarkan deret Mclaurin. Contoh penggunaannya pada perhitungan seperti sin x, cos x, log x, dan lainnya. Berikut contoh soal dan penyelesaian deret Mclaurin dan deret Taylor.
Materi lain yaitu metode Newton - Rhapson, dimana metode ini untuk mencari akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan. Metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih, maka semakin cepat konvergen ke akarnya.
Kemudian terdapat materi mengenai Regresi, interpolasi, dam materi lain yang berkaitan. Materi Regresi adalah metode dalam statistika untuk menentukan hubungan antar variabel satu dengan variabel lain. Fungsinya yaitu untuk mendapatkan kurva sebagai wakil data dari kumpulan data, dimana kurva dapat berbentuk garis linear. Interpolasi adalah perkiraan nilai titik data yang terletak diantara titik - titik data yang sudah diketahui dengan asumsi titik data tersebut dilewati suatu fungsi kurva tertentu. Fungsinya adalah mendapatkan nilai diantara dua titik data.
Terdapat juga materi mengenai turunan numerik dan turunan parsial. Turunan numerik yaitu menurunkan suatu fungsi denga menggunakan tabel atau software yang menggunakan konsep perhitungan yang sama dengan teori. Sedangkan turunan parsial adalah perubahan nilai suatu fungsi yang memiliki 2 variabel atau lebih secara sebagian atau tidak keseluruhan. Seperti f(z) = f(x.y), ketika kita menurunkan x maka y dianggap sebagai konstanta atau bisa disebut mencari turunan parsial z terhadap x.
Tutorial mempelajari software Open Modelica
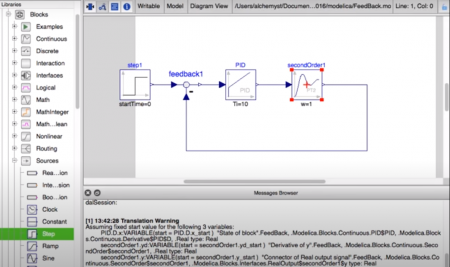
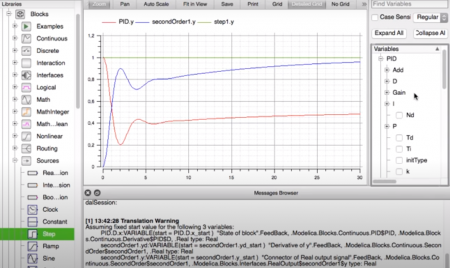
Pada tutorial yang penulis pelajari mengenai software Open Modelica, yaitu mengenai Simulasi sebuah feedback control system dengan referensi sebagai berikut.
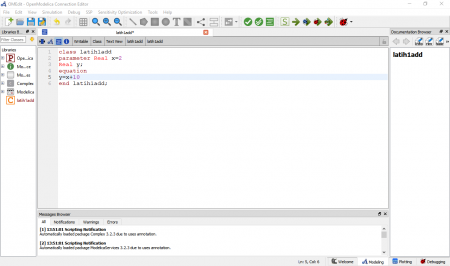
Tahap awal dalam simulasi yaitu melakukan pembuatan model untuk disimulasikan. Simulasi menggunakan sistem linear, dimana menggunakan simple second order system sebagai target untuk kontrol. Kemudian menggunakan PID control dimana pada Open modelica menggunakan tool continous. Selanjutnya memasukan blok ke area simulasi untuk PID control dan simple second order system. Berikutnya dengan menggunakan menu math digunakan tool feedback ke area simulasi, dan digunakan menu source berupa tool step, kemudian dikoneksikan untuk keseluruhan sistem. Cara dalam melakukan koneksi yaitu dengan melakukan drag untuk keselurah blok dan tools yang ada, membuat sistem menjadi closed loop. Berikut hasil dari sitem yang akan disimulasikan.
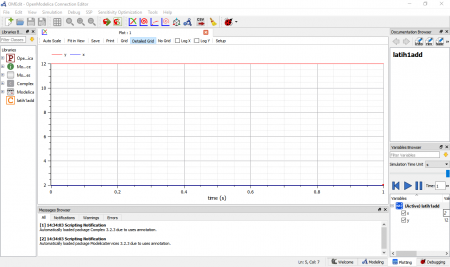
Tahap selanjutnya memasukan nilai parameter. Mengatur parameter untuk blok PID, kemudian second order block. Sistem menggunakan underdamped dengan nilai damping <1. Langkah setelahnya yaitu mengecek sistem dari perhitungan dimana didapatkan 22 persamaan dan 22 variabel. Simulasi dilakukan dengan menggunakan 30 interval. Kemudian saat melakukan simulasi file harus disimpan pada area yang ada, sebagai hasil data yang didapatkan. Pada hasil output data dari grafik kita dapat mendapatkan variabel seperti U dan y untuk contohnya. Padah hasil akhir simulasi yang didapat kita juga dapat mengubah parameter untuk mendapatkan variasi yang kita tentukan dan hasil simulasi hanya tinggal dilakukan kembali. Berikut hasil simulasi yang dihasilkan.
Tutorial Hasil Pembelajaran Open Modelica
Berdasarkan tugas metode numerik yang diberikan oleh Pak Dai, yaitu mengenai membuat tutorial video dalam mempelajari software Open Modelica. Berikut penulis lampirkan link video hasil pembelajaran tersebut.
Demikian hasil pembelajaran pada pertemuan pertama metode numerik dari penulis.
Wassalamualaikum Wr. Wb.
Pertemuan Metode Numerik 2 : 16 November 2020
Assalamualaikum Wr. Wb. pada kegiatan pembelajaran mata kuliah metode numerik hari ini. Pak Dai mengawali dengan mereview tugas yang diberikan pada pertemuan minggu lalu. Review tersebut mengenai software Open Modelica dan perhitungan yang masing - masing mahasiswa lakukan, dimana penulis menjelaskan mengenai sistem circuit sederhana. Terdapat dua resistor yaitu berupa 10 ohm dan 100 ohm pada parameternya. Kemudian terdapat voltage sebesar 220 v, kapasitor 0.01 F, dan Induktor 0.1 H. Hasil dari sistem tersebut didapatkan 39 persamaan dan 39 variabel. Berdasarkan hasil simulasi didapatkan plotting grafik dengan perubahan terhadap waktu, untuk masing - masing parameter yang dikerjakan.
Selanjutnya pertemuan hari ini, Pak Dai memberikan materi untuk membuat program menghitung rata - rata dari data. Berikut adalah lampiran dari tutorial yang diberikan oleh Pak Dai.
Dibuat menggunakan bahasa pemrograman untuk perhitungan yang akan digunakan. Pada percobaan pertama menghitung nilai x untuk persamaan y = x+10, kemudian mendapat nilai y.
Berikut adalah hasil simulasi yang dilakukan, dimana terdapat grafik dari hasil persaman apabila x = 2 maka y = 12, begitu pun untuk contoh x yang berbeda maka nilai y akan mengikuti dengan dijumlah 10.
Berikutnya adalah mencoba perhitungan untuk menentukan rata - rata dari kelompok data yang ada.
Kemudian terdapat hasil simulasi dari perhitungan untuk nilai dari masing - masing data dan hasil dari rata - rata yang didapatkan.
Pada hari ini, Pak Dai memberikan tugas mengenai perhitungan aljabar simultan. Aljabar simultan sendiri adalah penyelesaian matematik yang melibatkan kekompleksan yang sangat rumit sehingga memerlukan cara penyelesaian yang membuatnya sederhana dengan menggunakan tools yang ada, seperti komputer dengan program visual basic, matlab, atau lainnya.
Beberapa metode yang dapat diterapkan pada aljabar simultan seperti,
1. Metode Eliminasi Gauss
2. Metode Crammer
3. Metode Gauss Seidel
4. Metode Gauss-Jordan
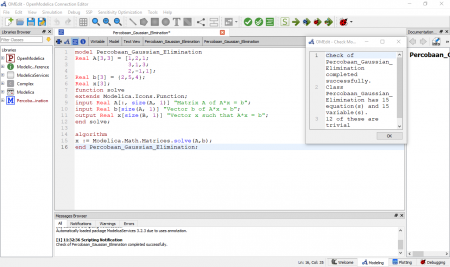
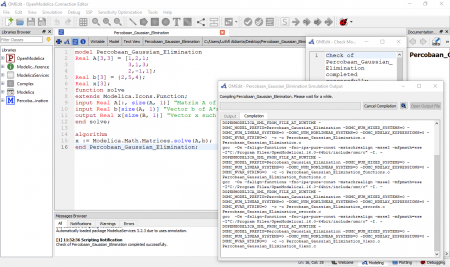
Berikut adalah hasil percobaan tugas penulis mengenai aljabar simultan dengan metode eliminasi Gauss. Penulis menggunakan referensi yang ada pada website openmodelica sebagai berikut.
link : https://build.openmodelica.org/Documentation/Modelica.Math.Matrices.solve.html
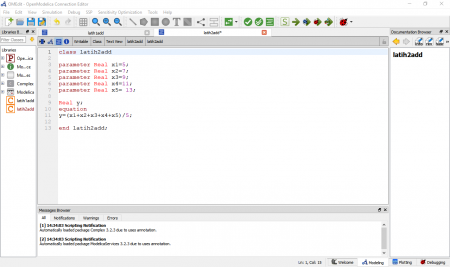
Dengan menggunakan persamaan,
X1 + 2X2 + X3 = 2
3X1 + X2 + 3x3 = 5
2X1 - X2 + x3 = 4
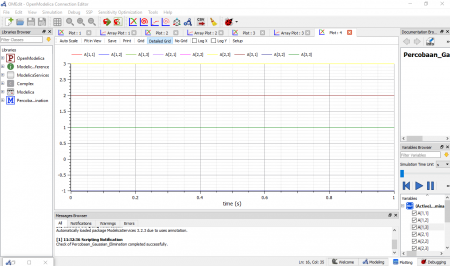
Didapatkan percobaan sebagai berikut.