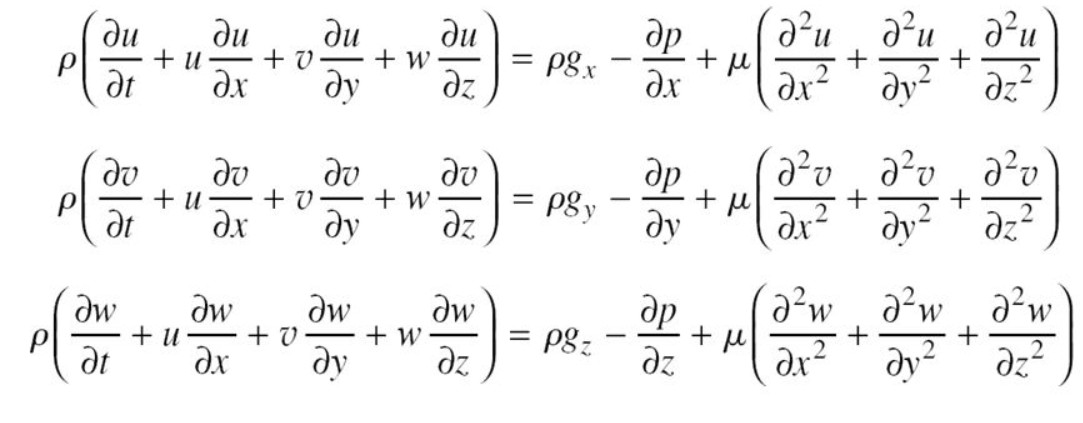Difference between revisions of "Hans Thiery T"
Hans.thiery (talk | contribs) (→Pertemuan 08 : 22 April 2020) |
Hans.thiery (talk | contribs) (→Pertemuan 05 : 14 April 2020) |
||
| Line 77: | Line 77: | ||
== Pertemuan 05 : 14 April 2020 == | == Pertemuan 05 : 14 April 2020 == | ||
Pada kuliah online kali ini, diadakan kuis berupa pembuatan artikel sesuai tema dari masing-masing soal yang ada pada wikipage http://air.eng.ui.ac.id/index.php?title=Soal-jawab_Mekanika_Fluida Artikel lalu dipost pada halaman soal tersebut. | Pada kuliah online kali ini, diadakan kuis berupa pembuatan artikel sesuai tema dari masing-masing soal yang ada pada wikipage http://air.eng.ui.ac.id/index.php?title=Soal-jawab_Mekanika_Fluida Artikel lalu dipost pada halaman soal tersebut. | ||
| + | |||
| + | Berikut merupakan artikel-artikel yang saya tulis. | ||
| + | |||
| + | 1. Analytical solution of laminar flow through the parallel- plate (Solusi analitik aliran laminar melalui pelat paralel) | ||
| + | |||
| + | Analisis simultan distribusi menghasilkan berbagai solusi yang diperlukan | ||
| + | |||
| + | Pengembangan simultan distribusi kecepatan dan suhu untuk aliran laminar di dalam saluran pelat paralel dipelajari secara analitik, dengan mengadopsi prosedur linierisasi untuk masalah kecepatan dan menyelesaikan persamaan energi yang dipisahkan melalui teknik transformasi integral yang digeneralisasi. Solusi lengkap diperoleh dalam jangkauan luas dari koordinat aksial, dari evaluasi numerik sistem transformasi integral persamaan diferensial biasa. Selain itu, perkiraan solusi eksplisit disediakan untuk perkiraan cepat dalam konteks aplikasi. Beberapa aspek diselidiki, seperti pengaruh konveksi transversal, efek dari profil kecepatan yang berbeda, konvergensi solusi lengkap, dan akurasi solusi perkiraan. | ||
| + | |||
| + | 2. Laminar Parallel Plate Flow (Alur Pelat Paralel Laminar) | ||
| + | |||
| + | Hubungan tekanan dengan luas penampang secara Nusselt dan model Darcy termodifikasi | ||
| + | |||
| + | Aliran laminar melalui saluran berpori yang dibatasi oleh dua pelat paralel yang dipertahankan pada suhu konstan dan sama dipertimbangkan. Model Darcy yang dimodifikasi untuk transportasi momentum diterapkan tetapi kecepatan dalam persamaan momentum dan konduksi aksial dalam persamaan energi diabaikan. Hasilnya menunjukkan bahwa bilangan Nusselt untuk bidang yang dikembangkan penuh meningkat dengan peningkatan parameter bentuk media berpori, | ||
| + | г = (W2 ɛ / K )12 | ||
| + | di mana W adalah lebar saluran, ɛ adalah porositas dan K adalah permeabilitas. | ||
| + | |||
| + | Hasilnya juga menunjukkan bahwa penurunan tekanan berlebih berbanding terbalik dengan luas penampang aliran masuk. | ||
| + | |||
| + | 3. Turbulent Parallel Plate Flow (Alur Plat Paralel Turbulen) | ||
| + | |||
| + | Aliran Turbulent dengan pendekatan mekanika statistik | ||
| + | |||
| + | Aliran Turbulent antara pelat paralel dipelajari dari pendekatan mekanika statistik yang menggunakan persamaan model, mirip dengan persamaan Boltzmann dari teori kinetik, yang diusulkan oleh Lundgren dari distribusi kecepatan elemen fluida. Solusi untuk persamaan ini diperoleh secara numerik, menggunakan metode ordinasi diskrit dan perbedaan hingga. Dua jenis kondisi batas pada fungsi distribusi dipertimbangkan, dan hasil perhitungan dibandingkan dengan data eksperimen yang tersedia. Sebuah penelitian menetapkan bahwa persamaan Lundgren memberikan deskripsi yang sangat baik tentang turbulensi untuk situasi aliran yang dipertimbangkan dan bahwa ia menawarkan alat analisis untuk studi lebih lanjut tentang aliran turbulen yang lebih kompleks. | ||
| + | |||
| + | 4. Laminar Pipe Flow (Aliran Pipa Laminar) | ||
| + | |||
| + | Persamaan Navier-Stokes pada laminar pipe flow | ||
| + | |||
| + | Aliran laminar dalam pipa lurus dapat dianggap sebagai gerakan relatif dari satu set silinder cairan konsentris, yang difiksasi pada dinding pipa dan yang lainnya bergerak dengan kecepatan yang meningkat ketika pusat pipa didekatkan. Contohnya asap yang naik di jalur lurus dari rokok yang beraliran laminar, namun setelah naik sedikit, asap biasanya berubah menjadi aliran turbulen. | ||
| + | |||
| + | Aliran laminar umum hanya dalam kasus di mana saluran aliran relatif kecil, fluida bergerak lambat, dan viskositasnya relatif tinggi. Aliran minyak melalui tabung tipis atau aliran darah melalui kapiler adalah laminar. Sebagian besar jenis aliran fluida lainnya adalah turbulen kecuali di dekat batas padat, di mana alirannya sering laminar, terutama dalam lapisan tipis yang berdekatan dengan permukaan. | ||
| + | |||
| + | Aliran laminar dalam tabung berdinding halus dari penampang lingkaran dengan jari-jari a, diasumsikan tidak dapat dimampatkan dan kecepatan aksial u adalah fungsi dari posisi radial r dan waktu t, tetapi seragam secara aksial. Cairan ini memiliki kepadatan r dan molekul viskositas kinematik v0. Viskositas kinematik efektif n{t} seragam dalam ruang, tetapi dapat bervariasi dalam waktu dengan cara yang ditentukan. Fungsi yang ditentukan n1{t} dengan mudah diskalakan sebagai | ||
| + | |||
| + | |||
| + | |||
| + | di mana n{t} adalah fungsi viskositas dan bagian variabelnya, n1 {t}, diasumsikan kontinu meskipun turunannya tidak perlu kontinu. Untuk aliran laminar yang tidak dapat dimampatkan sepenuhnya berkembang dalam pipa, persamaan gerak Navier- Stokes menunjukkan bahwa, tanpa adanya gaya benda yang signifikan, tekanannya seragam di atas penampang pipa dan merupakan fungsi linear dari koordinat aksial z. Akibatnya , gradien tekanan seragam di sepanjang pipa. Fungsi gradien tekanan, yang, secara umum, mungkin tergantung waktu, mudah didefinisikan sebagai | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Persamaan Navie-Stokes asimetri : | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | 5. Turbulent Pipe Flow Properties (Properti Aliran Pipa Turbulen) | ||
| + | |||
| + | Ilustrasi aliran turbulen dibandingkan dengan aliran lainnya | ||
| + | |||
| + | Aliran fluida dalam pipa bisa berupa aliran laminar atau aliran turbulen. Osborne Reynolds, seorang ilmuwan dan ahli matematika Inggris, adalah orang pertama yang membedakan perbedaan antara dua klasifikasi aliran ini dengan menggunakan peralatan sederhana seperti yang ditunjukkan pada Gambar.1. | ||
| + | Gambar 1: (a) Eksperimen Reynolds menggunakan air dalam pipa untuk mempelajari transisi menuju turbulensi, (b) Tingkatan pewarnaan khas | ||
| + | |||
| + | Jika air mengalir melalui pipa berdiameter D dengan kecepatan rata-rata V, karakteristik berikut diamati dengan menyuntikkan zat warna yang mengapung secara netral seperti yang ditunjukkan. Untuk laju aliran yang cukup kecil , goresan pewarna (streakline) akan tetap sebagai garis yang terdefinisi dengan baik karena mengalir sepanjang, dengan hanya sedikit kabur karena difusi molekul pewarna ke dalam air sekitarnya. Untuk aliran intermediate yang sedikit lebih besar, corak pewarna berfluktuasi dalam ruang dan waktu, dan semburan perilaku tidak teratur yang muncul di sepanjang coretan. Di sisi lain, untuk laju aliran yang cukup besar, lapisan pewarna segera menjadi kabur dan menyebar ke seluruh pipa secara acak. Ketiga karakteristik ini, dilambangkan sebagai aliran laminar, transisi, dan turbulen, masing-masing, diilustrasikan pada Gambar. 1b. | ||
| + | |||
| + | Untuk aliran pipa, parameter tanpa dimensi yang paling penting adalah angka Reynolds, Re =VD / n rasio inersia dengan efek viskos dalam aliran. Karenanya, istilah flowrate seharusnya digantikan oleh angka Reynolds, di mana V adalah kecepatan rata-rata dalam pipa. Yaitu aliran dalam pipa adalah laminar, transisi, atau turbulen asalkan angka Reynolds cukup kecil, menengah, atau cukup besar. Bukan hanya kecepatan fluida yang menentukan karakter aliran , densitas, viskositas, dan ukuran pipanya sama pentingnya. Parameter ini bergabung untuk menghasilkan angka Reynolds. | ||
| + | |||
| + | Perbedaan antara aliran pipa laminar dan turbulen dan ketergantungannya pada kuantitas berdimensi yang tepat pertama kali ditunjukkan oleh Osborne Reynolds pada tahun 1883. Rentang angka Reynolds yang diperoleh dari aliran pipa laminar, transisi, atau turbulen tidak dapat diberikan secara tepat . Transisi aktual dari aliran laminar ke turbulen dapat terjadi pada berbagai bilangan Reynolds , tergantung pada seberapa banyak alirannya terganggu oleh getaran pipa, kekasaran wilayah pintu masuk, dan sejenisnya. Untuk tujuan rekayasa umum (yaitu, tanpa tindakan pencegahan yang tidak semestinya untuk menghilangkan gangguan seperti itu), nilai-nilai berikut sesuai: Aliran dalam pipa bundar adalah laminar jika bilangan Reynolds kurang dari sekitar 2100. Aliran dalam pipa bundar bergolak jika Jumlah Reynolds lebih besar dari sekitar 4000. Untuk bilangan Reynolds antara dua batas ini, aliran dapat beralih antara kondisi laminar dan turbulen dalam aliran transisi mode acak). | ||
| + | |||
| + | 6. Comparison of Laminar or Turbulent Pressure Drop (Perbandingan Penurunan Laminar atau Turbulent Pressure) | ||
| + | Penerapan Segmented Baffles pada pressure drop | ||
| + | Pada penerapan Segmented Baffles dalam penurunan tekanan pipa secara signifikan meningkat dibandingkan dengan pipa lurus. Tekanan dinamis meningkat seiring dengan meningkatnya bilangan Reynolds tetapi jika dibandingkan dengan tekanan dinamis pipa lurus lebih signifikan pada baffle. Koefisien gesekan kulit meningkat dengan meningkatnya jumlah Reynolds dan gesekan kulit lebih penting pada pipa yang membingungkan. Dalam aliran laminar kehadiran baffle menciptakan turbulensi. Pada peningkatan bilangan Reynolds intensitas turbulen meningkat secara linear. Mempertimbangkan suhu mempengaruhi baffle memberikan keuntungan dalam meningkatkan kinerja termo-hidrodinamik. Tegangan geser dinding secara drastis meningkatkan kebingungan saat jumlah Reynolds meningkat. Karena adanya turbulensi dalam faktor gesekan pipa meningkat secara linear seiring dengan jumlah Reynolds. Mengintegrasikan permukaan yang diperluas dalam pipa dan saluran meningkatkan karakteristik perpindahan panas seiring dengan meningkatnya faktor gesekan. Oleh karena itu, banyak digunakan dalam desain penukar panas. | ||
== Pertemuan 06 : 15 April 2020 == | == Pertemuan 06 : 15 April 2020 == | ||
Revision as of 12:09, 28 April 2020
Nama : Hans Thiery T
NPM : 1806233341
Mata Kuliah : Mekanika Fluida Dasar
Contents
- 1 Pertemuan 01 : 31 Maret 2020
- 2 Pertemuan 02 : 01 April 2020
- 3 Pertemuan 03 : 07 April 2020
- 4 Pertemuan 04 : 08 April 2020
- 5 Pertemuan 05 : 14 April 2020
- 6 Pertemuan 06 : 15 April 2020
- 7 Pertemuan 07 : 21 April 2020
- 8 Pertemuan 08 : 22 April 2020
- 9 Pertemuan 09 : 28 April 2020
- 10 Pertemuan 10 : 29 April 2020
- 11 Pertemuan 11 : 05 Mei 2020
- 12 Pertemuan 12 : 06 Mei 2020
Pertemuan 01 : 31 Maret 2020
Pada kuliah online kali ini menggunakan aplikasi Zoom yang dipandu oleh Asisten Dosen Mekanika Fluida, Bang Edo Syafei. Perkuliahan dibagi menjadi dua sesi, yang pertama diberikan pengantar tentang bahan viskositas dan yang kedua tentang bagaimana menggunakan perangkat lunak CFDSOF yang akan digunakan dalam mata kuliah ini dan memberikan pula contoh kasus.
Melalui sharescreen, Bang Edo memberikan materi Aliran Viskos melalui presentasi powerpoint, yang intinya:
Aliran inviscid adalah aliran ideal, yang tidak memiliki kekentalan. Akan tetapi pada kenyataannya, tidak mungkin ada aliran yang inviscid. Pada praktiknya hanya ada aliran viscous yang efeknya dalam pipa adalah profil penampang aliran dalam pipa tidak sama.
Viskositas adalah ukuran ketahanan sebuah fluida terhadap deformasi atau perubahan bentuk. Bila suatu fluida mengalami geseran, ia mulai bergerak dengan laju regangan yang berbanding terbalik dengan suatu besaran yang disebut dengan koefisien kekentalan dinamik.
Reynolds number atau bilangan Reynolds adalah perbandingan rasio antara gaya inersia dengan gaya Viskos pada fluida. Bilangan reynolds bisa dituliskan dalam rumus: Re = V.D.ρ / µ = V.d / v
Melalui sharescreen, Bang Edo juga memberikan tutorial CFDSOF untuk membuat simulasi aliran udara dalam pipa pada bidang dua dimensi sebagai contoh kasus.
Tidak hanya itu, Bang Edo juga tidak lupa untuk memberikan tugas, sebagai pemicu untuk pertemuan selanjutnya, yaitu:
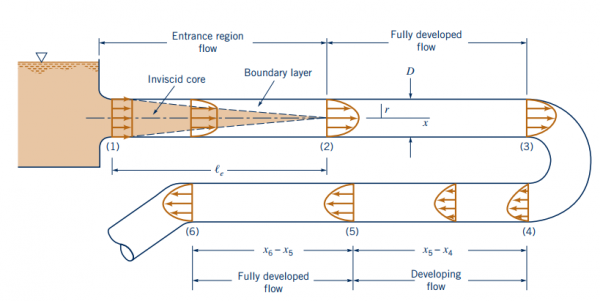
1. Apa itu entrance region atau aliran masuk?
Entrance region atau aliran masuk adalah wilayah yang dialiri fluida setelah memasuki pipa sebelum mencapai kondisi fully developed flow atau aliran yang berkembang sempurna.
2. Apa itu aliran berkembang sempurna / Fully developed flow ?
Fully developed flow atau aliran berkembang sempurna adalah kondisi fluida saat profil kecepatan tidak berubah lagi
3. Apa pengaruh viskositas dan pressure drop dalam pipa?
Pressure drop adalah penurunan tekanan yang terjadi akibat adanya gesekan pada fluida yang mengalir. Pressure drop akan semakin tinggi dan berbanding lurus dengan gesekan pada fluida. Sedangkan besarnya gesekan dipengaruhi oleh viskositas dari suatu fluida.
4. Bagaimana cara menghitung pressure drop suatu aliran dalam laminar/turbulen?
Cara mengukur pressure drop adalah selisih antara tekanan total fluida masuk dan tekanan total fluida keluar (Ptotal = Ps + Pd, dimana Ps = tekanan statis dan Pd = tekanan dinamis = 1/2 ρV^2)
5. Apa itu entrance length?
Entrance length adalah jarak dari aliran masuk pipa hingga aliran berkembang sempurna atau fully developed flow.
Pertemuan 02 : 01 April 2020
Pada kuliah online kali ini menggunakan aplikasi Zoom yang dipandu oleh Dosen dan Asisten Dosen Mekanika Fluida, Pak Ahmad Indra dan Bang Edo Syafei. Pada perkuliahan ini kita membahas tentang tiga rumus dasar dalam mekanika fluida, yaitu tiga hukun konservasi, yaitu konservasi massa, konservasi momentum, dan konservasi energi.
- Konservasi Massa
Massa sistem akan selalu konstan dari waktu ke waktu. Rumusnya: dm/dt = 0
- Konservasi Momentum
Hukum Newton II, yaitu suatu sistem mengalami percepatan bila ada gaya netto atau jumlah gaya tidak sama dengan nol. Rumusnya: m dV/dt = ΣF
- Konservasi Energi
Apabia sistem energi mengalami perubahan total harus diikuti perubahan dalam bentuk kerja dan panas. Rumusnya: dE/dt = W + Q
Lalu kita diberikan tutorial tentang bagaimana mencari pressure drop menggunakan CFD. Menggunakan kalkulator dalam CFD serta melakukan latihan soal seperti pada gambar dibawah ini.
Pertemuan 03 : 07 April 2020
Pada kuliah online kali ini kami membahas kembali soal minggu lalu mengenai laminar flow pada plat paralel oleh Pak Indra. Setelah itu, beliau menjelaskan governing equation, yaitu sebuah formula general yang digunakan dalam menganalisis aliran dalma fluida dengan pendekatan hukum hukum konservasi yang dituangkan dalam persamaan matematis. Persamaan 1 merupakan sebuah Governing Eq yang diturunkan dari Hukum kekekalan massa kemudian persamaan 2 merupakan persamaan momentum. Pada persamaan 2 diketahui bahwa tegangan geser hanya pada arah horizontal atau tidak ada profil kecepatan pada arah vertikal. Sehingga didapat fungsi kecepatan atau profil kecepatan terhadap Y atau u(Y).Governing equation ditulis sebagai berikut:
Pertemuan 04 : 08 April 2020
Pada kuliah online kali ini membahas tentang hubungan lapisan aliran fluida terhadap Reynold number. Jika menggunakan persamaan Re = inersia force/friction force, maka didapatkan bahwa semakin besar inersia maka semakin besar juga Rynold number yang didapatkan, sehingga semakin lama untuk mencapai keadaan fully development. Berkebalikan dengan itu, semakin besar viskositas maka semakin kecil bilangan Reynold dan semakin cepat mencapai keadaan aliran berkembang sempurna. dan hubungannya dengan jenis- jenis aliran adalah sebagai berikut :
Laminar = Memiliki lapisan fluida berlapis-lapis yang tersusun secara parallel dan tidak bertabrakan satu sama lain (tidak terjadi perpotongan antar lapisan fluida).
Transisi = Memiliki bentuk lapisan menyerupai osilasi dan terkadang terdapat perpotongan antar lapisan fluida akbat ketidakstabilan aliran. Aliran ini merupakan pembatas antara aliran laminar dan aliran turbolen.
Turbolen = Terjadi ketidakteraturan pada aliran lapisan fluida yang mengakibatkan terjadi perpotongan antar lapisan.
Hubungan antara Reynold number (Re) dengan jenis aliran adalah, jika menggunakan fluida yang sama kecepatan aliran pada aliran turbolen akan lebih cepat dibandingkan dengan aliran laminar karena Reynold number pada aliran turbolen lebih besar. Pengaruh lain jenis aliran adalah gaya gesek pada turbolen lebih kecil karena viskos tidak terlalu berpengaruh karena peranannya dibanding dengan inersia, sehingga mengakibatkan Reynold number semakin besar.
Pertemuan 05 : 14 April 2020
Pada kuliah online kali ini, diadakan kuis berupa pembuatan artikel sesuai tema dari masing-masing soal yang ada pada wikipage http://air.eng.ui.ac.id/index.php?title=Soal-jawab_Mekanika_Fluida Artikel lalu dipost pada halaman soal tersebut.
Berikut merupakan artikel-artikel yang saya tulis.
1. Analytical solution of laminar flow through the parallel- plate (Solusi analitik aliran laminar melalui pelat paralel)
Analisis simultan distribusi menghasilkan berbagai solusi yang diperlukan
Pengembangan simultan distribusi kecepatan dan suhu untuk aliran laminar di dalam saluran pelat paralel dipelajari secara analitik, dengan mengadopsi prosedur linierisasi untuk masalah kecepatan dan menyelesaikan persamaan energi yang dipisahkan melalui teknik transformasi integral yang digeneralisasi. Solusi lengkap diperoleh dalam jangkauan luas dari koordinat aksial, dari evaluasi numerik sistem transformasi integral persamaan diferensial biasa. Selain itu, perkiraan solusi eksplisit disediakan untuk perkiraan cepat dalam konteks aplikasi. Beberapa aspek diselidiki, seperti pengaruh konveksi transversal, efek dari profil kecepatan yang berbeda, konvergensi solusi lengkap, dan akurasi solusi perkiraan.
2. Laminar Parallel Plate Flow (Alur Pelat Paralel Laminar)
Hubungan tekanan dengan luas penampang secara Nusselt dan model Darcy termodifikasi
Aliran laminar melalui saluran berpori yang dibatasi oleh dua pelat paralel yang dipertahankan pada suhu konstan dan sama dipertimbangkan. Model Darcy yang dimodifikasi untuk transportasi momentum diterapkan tetapi kecepatan dalam persamaan momentum dan konduksi aksial dalam persamaan energi diabaikan. Hasilnya menunjukkan bahwa bilangan Nusselt untuk bidang yang dikembangkan penuh meningkat dengan peningkatan parameter bentuk media berpori, г = (W2 ɛ / K )12 di mana W adalah lebar saluran, ɛ adalah porositas dan K adalah permeabilitas.
Hasilnya juga menunjukkan bahwa penurunan tekanan berlebih berbanding terbalik dengan luas penampang aliran masuk.
3. Turbulent Parallel Plate Flow (Alur Plat Paralel Turbulen)
Aliran Turbulent dengan pendekatan mekanika statistik
Aliran Turbulent antara pelat paralel dipelajari dari pendekatan mekanika statistik yang menggunakan persamaan model, mirip dengan persamaan Boltzmann dari teori kinetik, yang diusulkan oleh Lundgren dari distribusi kecepatan elemen fluida. Solusi untuk persamaan ini diperoleh secara numerik, menggunakan metode ordinasi diskrit dan perbedaan hingga. Dua jenis kondisi batas pada fungsi distribusi dipertimbangkan, dan hasil perhitungan dibandingkan dengan data eksperimen yang tersedia. Sebuah penelitian menetapkan bahwa persamaan Lundgren memberikan deskripsi yang sangat baik tentang turbulensi untuk situasi aliran yang dipertimbangkan dan bahwa ia menawarkan alat analisis untuk studi lebih lanjut tentang aliran turbulen yang lebih kompleks.
4. Laminar Pipe Flow (Aliran Pipa Laminar)
Persamaan Navier-Stokes pada laminar pipe flow
Aliran laminar dalam pipa lurus dapat dianggap sebagai gerakan relatif dari satu set silinder cairan konsentris, yang difiksasi pada dinding pipa dan yang lainnya bergerak dengan kecepatan yang meningkat ketika pusat pipa didekatkan. Contohnya asap yang naik di jalur lurus dari rokok yang beraliran laminar, namun setelah naik sedikit, asap biasanya berubah menjadi aliran turbulen.
Aliran laminar umum hanya dalam kasus di mana saluran aliran relatif kecil, fluida bergerak lambat, dan viskositasnya relatif tinggi. Aliran minyak melalui tabung tipis atau aliran darah melalui kapiler adalah laminar. Sebagian besar jenis aliran fluida lainnya adalah turbulen kecuali di dekat batas padat, di mana alirannya sering laminar, terutama dalam lapisan tipis yang berdekatan dengan permukaan.
Aliran laminar dalam tabung berdinding halus dari penampang lingkaran dengan jari-jari a, diasumsikan tidak dapat dimampatkan dan kecepatan aksial u adalah fungsi dari posisi radial r dan waktu t, tetapi seragam secara aksial. Cairan ini memiliki kepadatan r dan molekul viskositas kinematik v0. Viskositas kinematik efektif n{t} seragam dalam ruang, tetapi dapat bervariasi dalam waktu dengan cara yang ditentukan. Fungsi yang ditentukan n1{t} dengan mudah diskalakan sebagai
di mana n{t} adalah fungsi viskositas dan bagian variabelnya, n1 {t}, diasumsikan kontinu meskipun turunannya tidak perlu kontinu. Untuk aliran laminar yang tidak dapat dimampatkan sepenuhnya berkembang dalam pipa, persamaan gerak Navier- Stokes menunjukkan bahwa, tanpa adanya gaya benda yang signifikan, tekanannya seragam di atas penampang pipa dan merupakan fungsi linear dari koordinat aksial z. Akibatnya , gradien tekanan seragam di sepanjang pipa. Fungsi gradien tekanan, yang, secara umum, mungkin tergantung waktu, mudah didefinisikan sebagai
Persamaan Navie-Stokes asimetri :
5. Turbulent Pipe Flow Properties (Properti Aliran Pipa Turbulen)
Ilustrasi aliran turbulen dibandingkan dengan aliran lainnya
Aliran fluida dalam pipa bisa berupa aliran laminar atau aliran turbulen. Osborne Reynolds, seorang ilmuwan dan ahli matematika Inggris, adalah orang pertama yang membedakan perbedaan antara dua klasifikasi aliran ini dengan menggunakan peralatan sederhana seperti yang ditunjukkan pada Gambar.1. Gambar 1: (a) Eksperimen Reynolds menggunakan air dalam pipa untuk mempelajari transisi menuju turbulensi, (b) Tingkatan pewarnaan khas
Jika air mengalir melalui pipa berdiameter D dengan kecepatan rata-rata V, karakteristik berikut diamati dengan menyuntikkan zat warna yang mengapung secara netral seperti yang ditunjukkan. Untuk laju aliran yang cukup kecil , goresan pewarna (streakline) akan tetap sebagai garis yang terdefinisi dengan baik karena mengalir sepanjang, dengan hanya sedikit kabur karena difusi molekul pewarna ke dalam air sekitarnya. Untuk aliran intermediate yang sedikit lebih besar, corak pewarna berfluktuasi dalam ruang dan waktu, dan semburan perilaku tidak teratur yang muncul di sepanjang coretan. Di sisi lain, untuk laju aliran yang cukup besar, lapisan pewarna segera menjadi kabur dan menyebar ke seluruh pipa secara acak. Ketiga karakteristik ini, dilambangkan sebagai aliran laminar, transisi, dan turbulen, masing-masing, diilustrasikan pada Gambar. 1b.
Untuk aliran pipa, parameter tanpa dimensi yang paling penting adalah angka Reynolds, Re =VD / n rasio inersia dengan efek viskos dalam aliran. Karenanya, istilah flowrate seharusnya digantikan oleh angka Reynolds, di mana V adalah kecepatan rata-rata dalam pipa. Yaitu aliran dalam pipa adalah laminar, transisi, atau turbulen asalkan angka Reynolds cukup kecil, menengah, atau cukup besar. Bukan hanya kecepatan fluida yang menentukan karakter aliran , densitas, viskositas, dan ukuran pipanya sama pentingnya. Parameter ini bergabung untuk menghasilkan angka Reynolds.
Perbedaan antara aliran pipa laminar dan turbulen dan ketergantungannya pada kuantitas berdimensi yang tepat pertama kali ditunjukkan oleh Osborne Reynolds pada tahun 1883. Rentang angka Reynolds yang diperoleh dari aliran pipa laminar, transisi, atau turbulen tidak dapat diberikan secara tepat . Transisi aktual dari aliran laminar ke turbulen dapat terjadi pada berbagai bilangan Reynolds , tergantung pada seberapa banyak alirannya terganggu oleh getaran pipa, kekasaran wilayah pintu masuk, dan sejenisnya. Untuk tujuan rekayasa umum (yaitu, tanpa tindakan pencegahan yang tidak semestinya untuk menghilangkan gangguan seperti itu), nilai-nilai berikut sesuai: Aliran dalam pipa bundar adalah laminar jika bilangan Reynolds kurang dari sekitar 2100. Aliran dalam pipa bundar bergolak jika Jumlah Reynolds lebih besar dari sekitar 4000. Untuk bilangan Reynolds antara dua batas ini, aliran dapat beralih antara kondisi laminar dan turbulen dalam aliran transisi mode acak).
6. Comparison of Laminar or Turbulent Pressure Drop (Perbandingan Penurunan Laminar atau Turbulent Pressure) Penerapan Segmented Baffles pada pressure drop Pada penerapan Segmented Baffles dalam penurunan tekanan pipa secara signifikan meningkat dibandingkan dengan pipa lurus. Tekanan dinamis meningkat seiring dengan meningkatnya bilangan Reynolds tetapi jika dibandingkan dengan tekanan dinamis pipa lurus lebih signifikan pada baffle. Koefisien gesekan kulit meningkat dengan meningkatnya jumlah Reynolds dan gesekan kulit lebih penting pada pipa yang membingungkan. Dalam aliran laminar kehadiran baffle menciptakan turbulensi. Pada peningkatan bilangan Reynolds intensitas turbulen meningkat secara linear. Mempertimbangkan suhu mempengaruhi baffle memberikan keuntungan dalam meningkatkan kinerja termo-hidrodinamik. Tegangan geser dinding secara drastis meningkatkan kebingungan saat jumlah Reynolds meningkat. Karena adanya turbulensi dalam faktor gesekan pipa meningkat secara linear seiring dengan jumlah Reynolds. Mengintegrasikan permukaan yang diperluas dalam pipa dan saluran meningkatkan karakteristik perpindahan panas seiring dengan meningkatnya faktor gesekan. Oleh karena itu, banyak digunakan dalam desain penukar panas.
Pertemuan 06 : 15 April 2020
Pertemuan 07 : 21 April 2020
Pertemuan 08 : 22 April 2020
Pada kuliah online kali ini, masing-masing mahasiswa diminta untuk menjelaskan tentang hal yang paling dipahami selama belajar mekanika fluida dan memperlihatkan kontribusi nya pada wikipage. Saya menjelaskan tentang perbedaan aliran laminar, turbulent, dan transitional. Salah satu konsep dasar yang wajib untuk dipahami adalah perbedaan antara aliran-aliran tersebut, sehingga saya memilih untuk menjelaskan hal tersebut.
Kesimpulan yang saya dapatkan bahwa setiap aliran dapat dibedakan dengan angka Reynold yang didapatkan, serta perbedaan aliran tersebut akan memberikan fungsi dan efek yang berbeda untuk penyesuaian desain mekanikal.