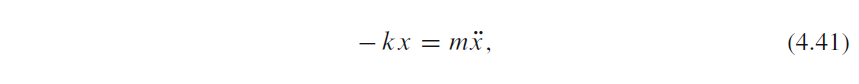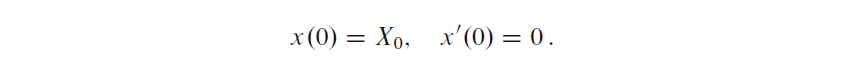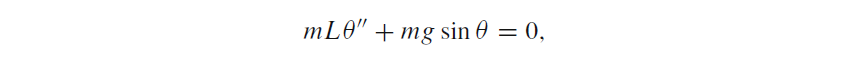Difference between revisions of "Oscillating one-dimensional systems"
(→4.3,13 Metode finite diference; damping linier) |
|||
| Line 146: | Line 146: | ||
[[File:4.82.png]] | [[File:4.82.png]] | ||
| − | '''4.3.4 Sebuah Penyelesaian dari Metode Numerik ''' | + | ==== '''4.3.4 Sebuah Penyelesaian dari Metode Numerik ''' ==== |
Dalam skema Forward Euler, | Dalam skema Forward Euler, | ||
Revision as of 15:36, 10 April 2020
Contents
[hide]Studi kasus dan Terjemahan
Ref. Linge S, Langtangen HP, Programming for Computations - A Gentle Introduction to Numerical Simulations with Python
Terjemahan
4.3.1 Penurunan Model yang Sederhana
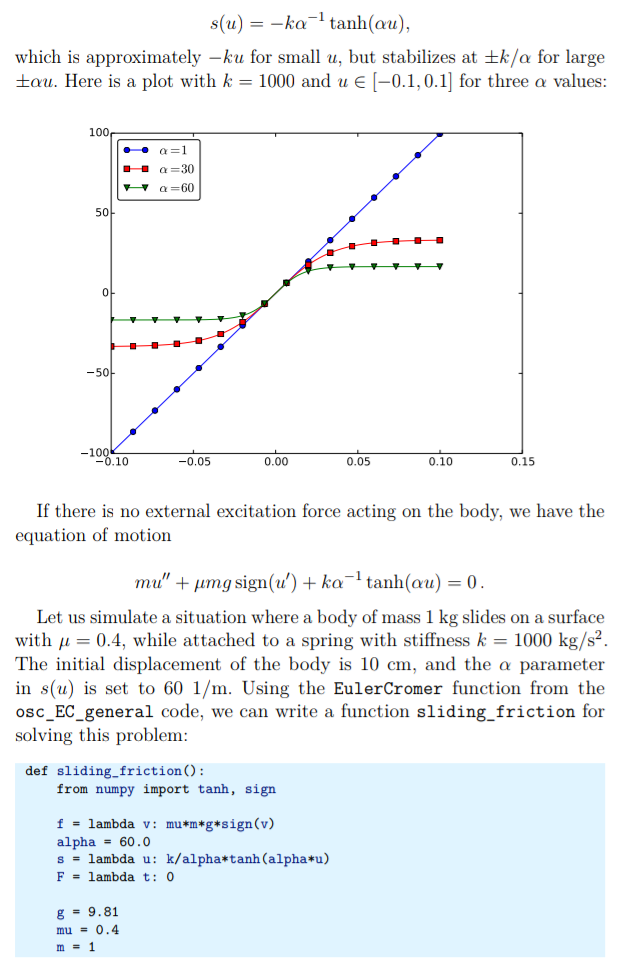
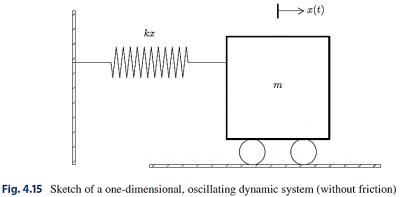
Banyak sistem keteknikan (engineering) berkaitan dengan osilasi, dan persamaan diferensial merupakan kunci utama untuk memahami, memprediksi, dan mengontrol osilasi. Kita mulai dengan model paling sederhana yang berkaitan dengan dinamika penting dari sistem osilasi. suatu benda dengan massa m melekat/dikaitkan pada pegas dan bergerak sepanjang garis tanpa gesekan, lihat Gambar 4.15 di samping untuk sketsa (rolling wheels menunjukkan “tidak ada gesekan”). Ketika pegas diregangkan (atau dikompresi), gaya pegas menarik (atau mendorong) bodi (penampang m) kembali dan bekerja "melawan" gerakan. Lebih tepatnya, misalkan x (t) adalah posisi bodi pada sumbu x, dimana bodi bergerak. Pegas tidak direntangkan ketika x= 0, sehingga gaya adalah nol, dan x= 0 karenanya posisi keseimbangan bodi. Gaya pegas adalah -kx, dimana k adalah konstanta yang diukur. Kami berasumsi bahwa tidak ada gaya lain (mis., Tidak ada gesekan). Hukum Newton ke-2 F=ma kemudian memiliki F=-kx dan a=x ̈ ,yang dapat ditulis ulang sebagai:
dengan memperkenalkan ω=√(k/m) (yang sangat umum).
Persamaan (4.42) adalah persamaan diferensial orde kedua, dan oleh karena itu kita memerlukan dua kondisi awal, satu pada posisi x(0) dan satu pada kecepatan x’(0). Di sini kita memilih bodi untuk berhenti, tetapi menjauh dari posisi setimbang:
Solusi tepat untuk Pers. (4.42) dengan kondisi awal ini adalah x(t)=X0 cosωT. Ini dapat dengan mudah diverifikasi dengan mensubsitusikan ke Pers. (4.42) dan memeriksa kondisi awal. Solusinya mengatakan bahwa sistem massa pegas berosilasi bolak-balik seperti yang dijelaskan oleh kurva kosinus.
Persamaan diferensial (4.42) muncul dalam banyak konteks lainnya. Contoh klasik adalah pendulum sederhana yang berosilasi bolak-balik. Buku-buku fisika berasal, dari hukum gerak kedua Newton, itu diperoleh:
dimana m adalah massa bodi di ujung pendulum dengan panjang L, g adalah percepatan gravitasi, dan ϴ merupakan sudut yang dibuat pendulum dengan vertikal. Mempertimbangkan sudut kecil ϴ, sin ϴ ≈ ϴ, dan kita dapatkan Pers. (4.42) dengan x = ϴ, ω=√(g/L) , x(0)=Θ, dan x’(0)=0, jika Θ merupakan sudut awal dan pendulum diam di t=0.
4.3.2 Solusi Numerik
Kita telah melihat metode numerik untuk mengendalikan turunan orde kedua, dan beberapa pilihan lainnya merupakan tambahan, akan tetapi kita mengetahu cara menyelesaikan persamaan turunan orde pertama dan bahkan sistem-sistem pada persamaan orde pertama. Dengan hanya sedikit, tetapi cukup umum, cara yang dapat kita tuliskan pada persamaan 4.42 sebagai sebuah sistem orde pertama dari 2 persamaan turunan. Kita memperkenalkan u=x dan v=x^'=u' sebagai 2 fungsi baru yang tidak diketahui. Dua persamaan yang sesuai muncul dari definisi v=u' dan persamaan asal (4.42):
(memperlihatkan bahwa kita dapat menggunakan u"=v') untuk menghilangkan turunan orde kedua dari hokum kedua newton). Selanjutnya kita dapat menerapkan metode forward euler untuk persamaan 4.43 dan 4.44, seperti yang sudah dilakukan pada section 4.2.2:
(u^(n+1)-u^n)/∆t=v^n (v^(n+1)-v^n)/∆t=〖-ω〗^2 u^n Sehingga menghasilkan skema komputasi sebagai berikut, u^(n+1)=u^n+∆tv^n 4.47 v^(n+1)=v^n-∆t〖ω^2 u〗^n 4.48
4.3.13 Metode finite diference; damping linier
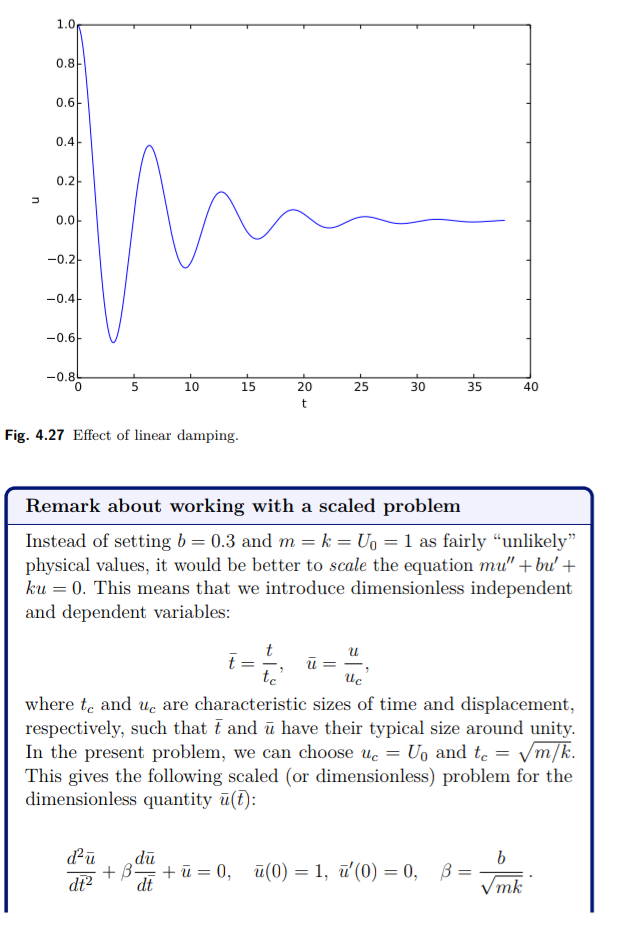
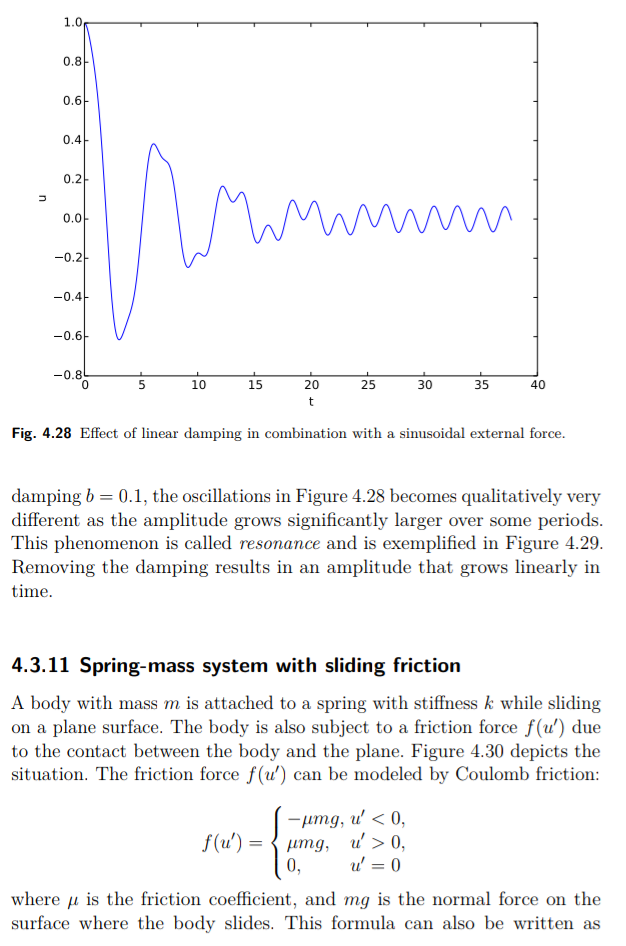
Sebuah isu kunci adalah bagaimana untuk mengkonferensi skema dari daerah 4.3.12 ke persamaan diferensial dengan lebih banyak istilah. Kita mulai dengan kasus linear penempatan f (u') = bu', kemungkinan gaya per nonlinear s(u), dan sebuah gaya excitation F(t):
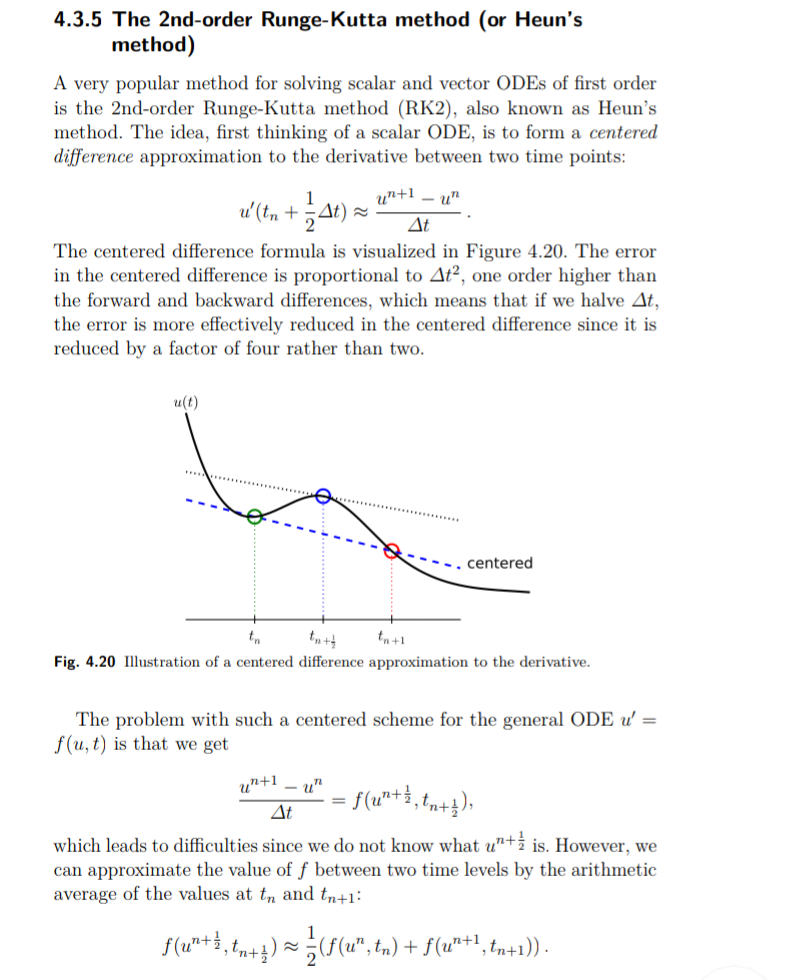
Kita harus cari perkiraan perbedaan yang tepat untuk u' di dalam bu'. Sebuah pilihan yang baik adalah perbedaan berpusat
2,4 t
Sampling persamaan pada titik t,,
dan memasukkan perkiraan perbedaan finete pada u" dan u / hasil dalam
dimana F" adalah notasi pendek untuk F(t). Persamaan (4.81) adalah linear dalam
u " +1 tak diketahui kita dapat dengan mudah memecahkan untuk kuantitas ini:
4.3.4 Sebuah Penyelesaian dari Metode Numerik
Dalam skema Forward Euler,
kita dapat mengganti un pada persamaan terakhir dengan nilai unC1 yang baru dihitung dari persamaan pertama:
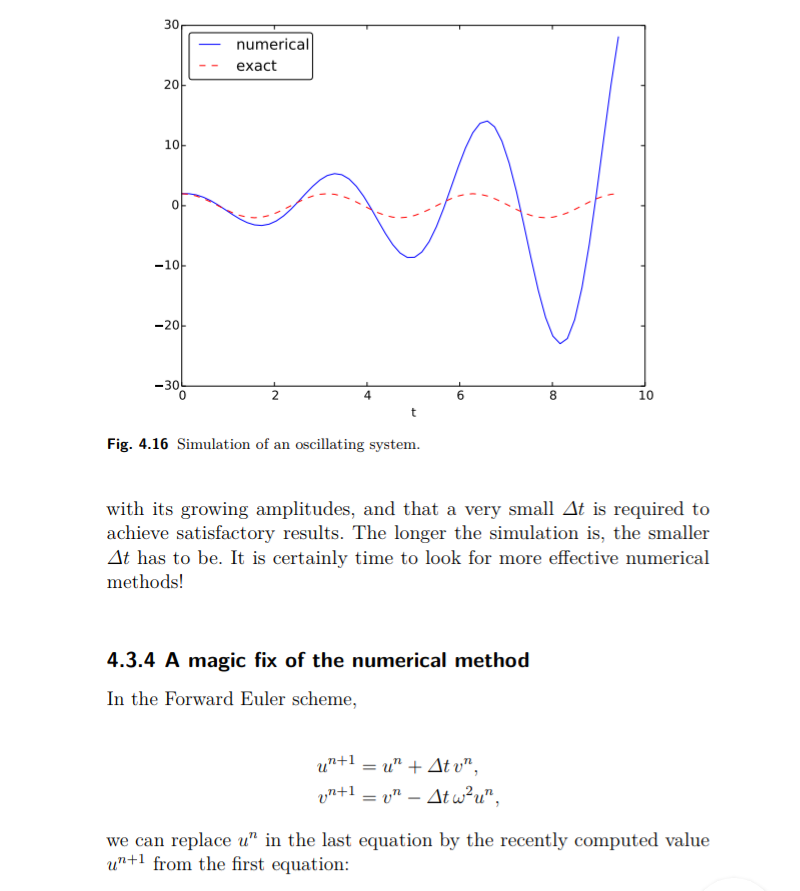
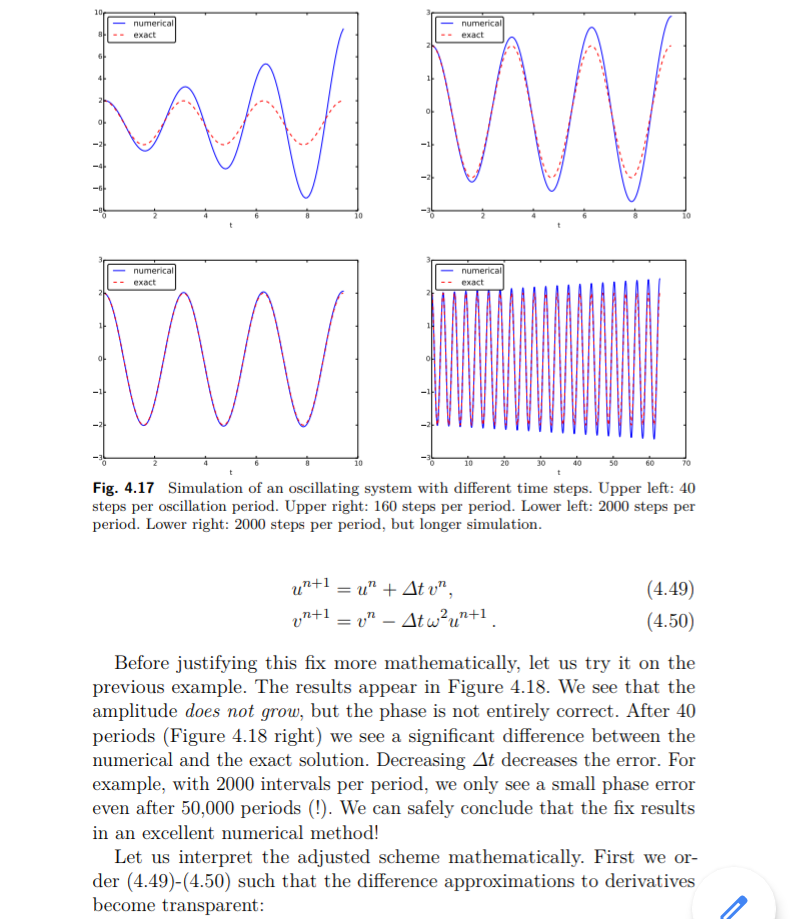
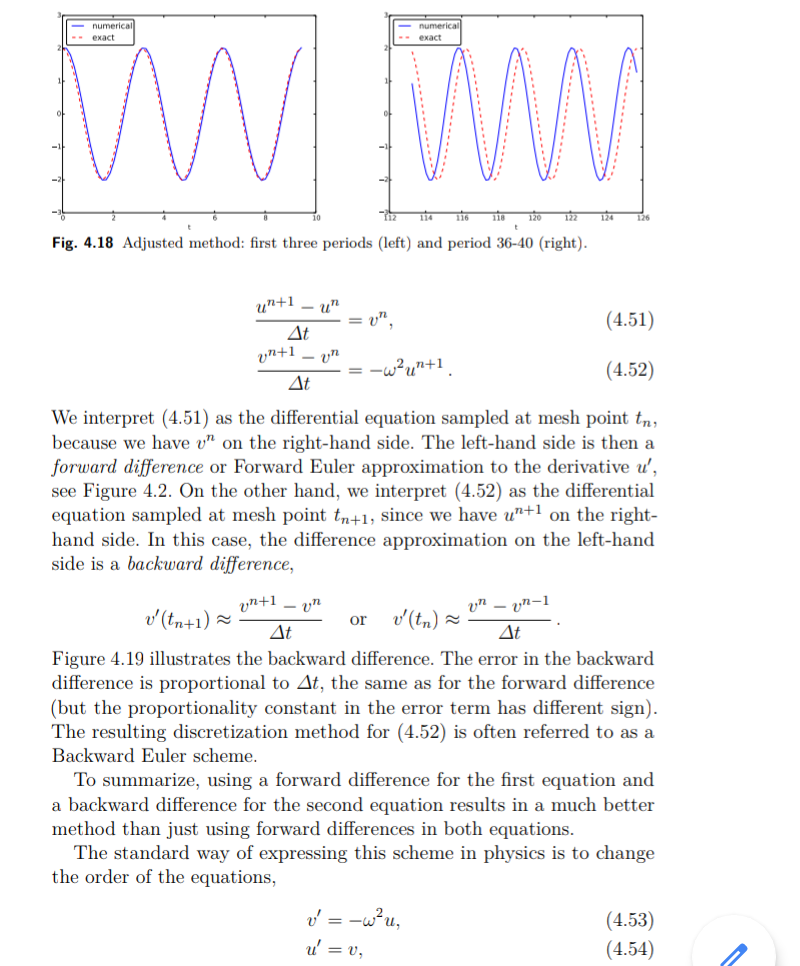
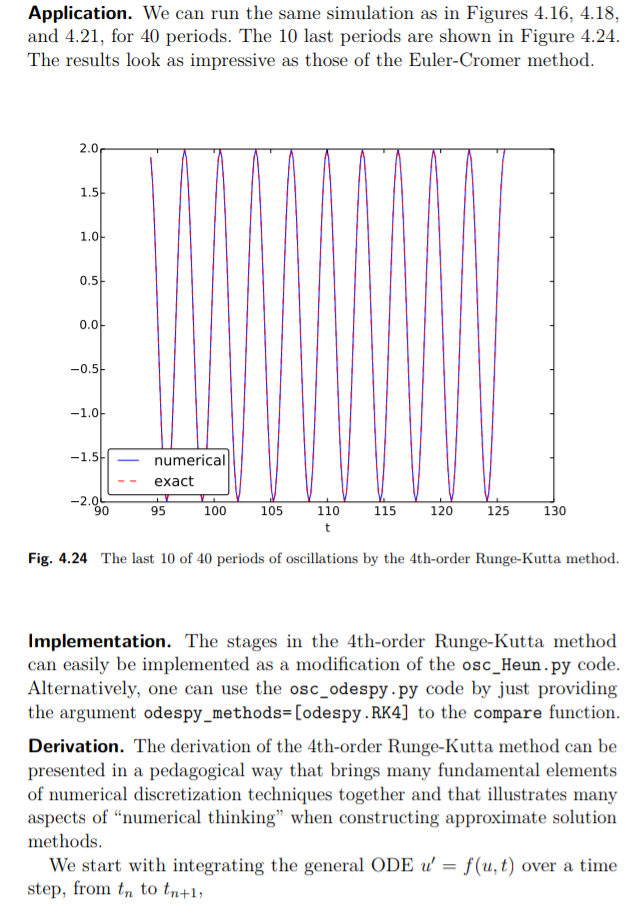
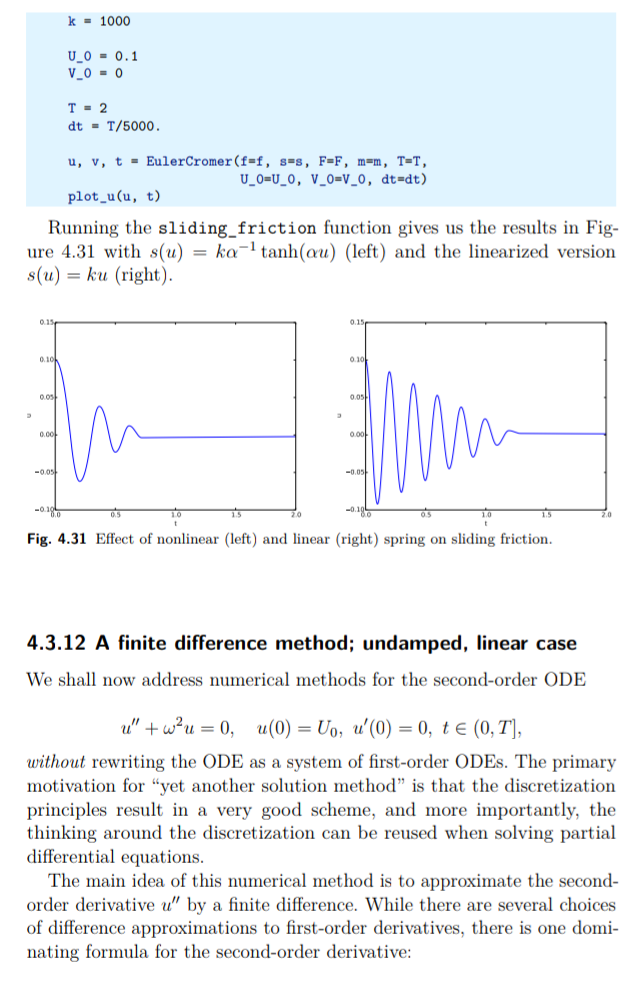
Sebelum membenarkan perbaikan ini secara matematis, mari kita coba pada contoh sebelumnya. Hasilnya muncul pada Gambar 4.18. Kita melihat bahwa amplitudo tidak tumbuh, tetapi fase tidak sepenuhnya benar. Setelah 40 periode (Gbr. 4.18 kanan) kita melihat signifikan perbedaan antara solusi numerik dan tepat. Penurunan t menurun kesalahan. Misalnya, dengan 2000 interval per periode, kami hanya melihat fase kecil kesalahan bahkan setelah 50.000 periode (!). Kita dapat menyimpulkan bahwa perbaikan tersebut menghasilkan metode numerik yang sangat baik! Mari kita tafsirkan skema yang disesuaikan secara matematis. Pertama kami memesan (4,49) - (4,50) sedemikian rupa sehingga perbedaan pendekatan terhadap derivatif menjadi transparan: (4,51)
(4,52)
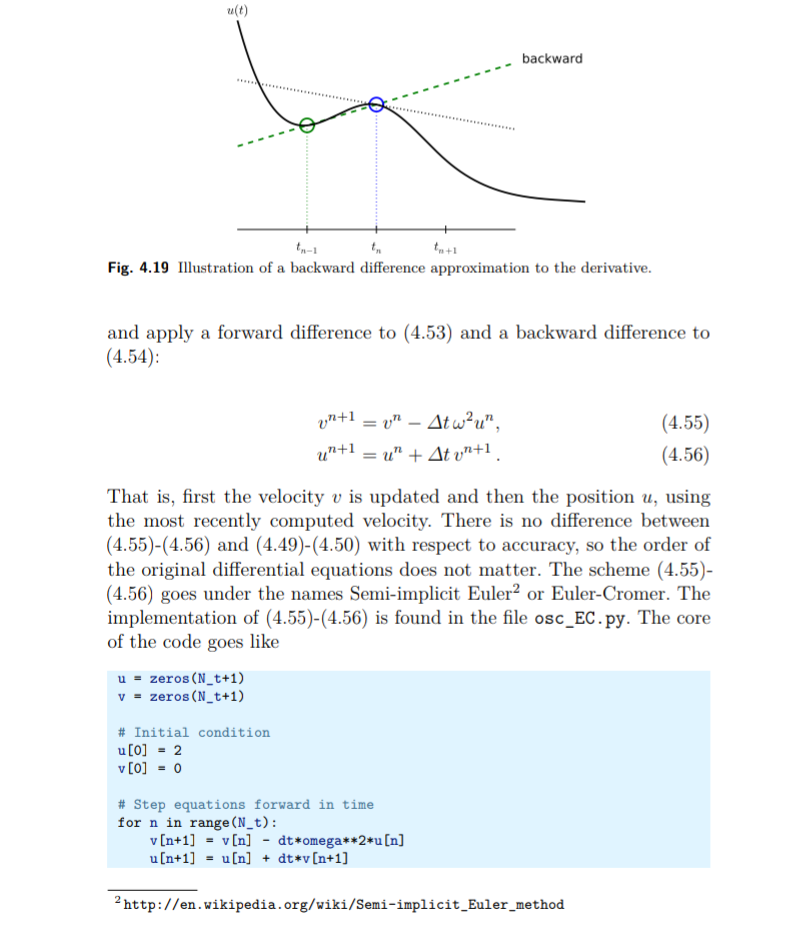
Kami menafsirkan (4,51) sebagai persamaan diferensial sampel pada titik mesh tn, karena
kami memiliki vn di sisi kanan. Sisi kiri kemudian perbedaan maju atau
Meneruskan perkiraan Euler ke turunan u0
, lihat Gambar 4.2. Di samping itu,
kami menginterpretasikan (4,52) sebagai persamaan diferensial sampel pada titik mesh tnC1, karena kami