Bhismantyo Tsaqif Daniswara

Bhismantyo Tsaqif Daniswara, Mahasiswa Teknik Mesin, Fakultas Teknik Universitas Indonesia

بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ

Biodata Diri

Nama  : Bhismantyo Tsaqif Daniswara

NPM  : 1806181754

Program Studi : S1 Pararel Teknik Mesin

Pertemuan 1 : Aliran Viskos(31 Maret 2020)

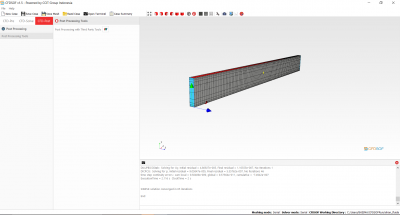
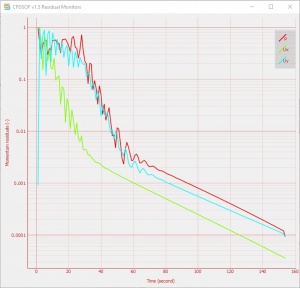
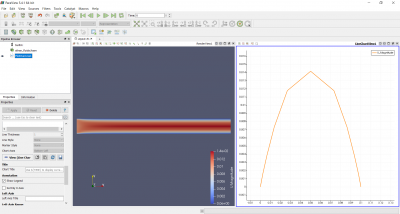
Pertemuan pertama dipimpin oleh Pak Muhammad Hilman, yang akbrab dipanggil mas Edo. Pada pertemuan ini, kami diajarkan mengenai aplikasi CFDSOF v.15, yakni aplikasi yang dapat menampilkan simulasi air flow dari dalam sebuah media. Aplikasi ini juga dapat membantu menyelesaikan masalah air flow pada kehidupan nyata.

Pertama-tama, kami menentukan terlebih dahulu bentuk geometrinya, lalu menentukan boundary name pada masing masing axis x,y dan z. Setelah itu, kami menentukan boundary conditions pada masing-masing axis. Lalu yang terakhir ialah melakukan simulasi pada geometri yang telah kami buat sebelumnya.

Lampiran :

Bentuk contoh geometri yang kami buat

Grafik residual monitor

Bentuk grafik dengan menggunakan ParaView

Pada pertemuan ini, Mas Edo juga memberikan materi mengenai "Aliran Viskos" yang membahas mengenai Laminar flow dan Turbulent flow, serta memberi beberapa pertanyaan:

1. Apa itu entrance region/aliran masuk?
2. Apa itu fully developed flow/aliran berkembang sempurna?
3. Apa itu entrance length?
4. Apa pengaruh viskositas? dan pengaruh pressure drop dalam pipa?
5. Bagaimana cara menghitung pressure drop suatu aliran dalam laminar/turbulen?

Jawaban :

1. Entrance region/aliran masuk adalah area pintu masuk saluran fluida sesuai pada gambar yang diberikan. Bagian saluran di mana kecepatan dan/atau suhu tidak sepenuhnya berkembang.Hal ini hanya bergantung pada kondisi awal atau kondisi masuknya fluida ke dalam pipa dimana lapisan batas meningkat hingga mengisi seluruh bagian melintang pipa.

2. Aliran berkembang sempurna adalah aliran pada suatu daerah setelah Entrance region flow. Dimana pada aliran ini, fluida sudah keluar dari boundary layer dan sudah tidak dipengaruhi oleh efek viskositas. Hal ini terjadi ketika fluida berjalan melalui pipa yang penampangnya lurus. Kecepatan fluida untuk aliran berkembang ini titik tercepatnya adalah di garis tengah pipa tersebut.

3. Entrance length adalah jarak yang ditempuh aliran fluida setelah memasuki pipa tepat sebelum aliran berkembang sepenuhnya atau dapat disebut juga jarak ketika aliran masuk Entrance Region sampai sebelum masuk ke Fully Developed Flow.

4. Viskositas sendiri dapat diartikan kepekatan fluida yang dapat menjelaskan besar kecil sentuhan dalam fluida. Dalam pipa semakin besar viskositas semakin sulit fluida dalam pipa untuk bergerak. Sebagai contoh jika fluida berupa air dan oli dialirkan dalam suatu pipa, maka air akan lebih cepat mengalir karena viskositas air lebih kecil dari oli dan molekul air yang bersentuhan dengan area pipa lebih cepat mengalir. Pressure drop dideskripsikan penurunan tekanan dari satu titik dalam sistem contohnya pipa ke titik lain yang memiliki tekanan lebih rendah. Dalam aplikasinya pada pipa pressure drop meningkat sebanding dengan gesekan dalam jaringan pipa, begitupun sebaliknya.

5. Rumus :

                                                            ΔP = f.1/2.l/D.ρ.V^2  
                                                                 f = 64/Re

Keterangan :

ΔP = Pressure drop (perbedaan tekanan) (Pa)

l = Panjang pipa pengukuran tekanan (m)

D = diameter pipa (m)

ρ = Densitas fluida (kg/m^3)

V = Kecepatan aliran fluida (m/s)

Re = Bilangan Reynold : Laminar (<2100) Turbulen (>2100)

Pertemuan 2 : Hukum Konservasi (1 April 2020)

Pada peretemuan kedua ini, dipimpin oleh Pak Ahmad Indra atau biasa dipanggil pak DAI. Pak DAI membahas mengenai Hukum Konservasi, yang dibagi menjadi 3, yaitu :

1. Kosnervasi Massa

  <math>\frac {\part m}{\part t} = 0</math>

2. Konservasi Momentum

  <math>M \middot \frac {\part V}{\part t} = \sum F</math>

<math>2x</math>

<math>2x \times 4y \div 6z + 8 - \frac {y}{z^2} = 0</math>

<math>\mathrm{u}(t)=\mathrm{P}(t)=K_p{e(t)} + K_{i}\int_{0}^{t}{e(\tau)}\,{d\tau} + K_{d}\frac{de(t)}{dt}</math>