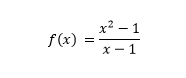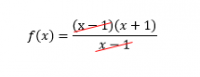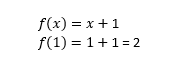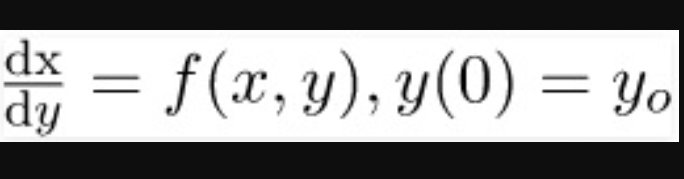Indonesia Sakti Darmanto

alt text

Saya Indonesia Sakti Darmanto, biasa dipanggil Indo, mahasiswa Teknik Perkapalan Universitas Indonesia angkatan 2018. Saya lahir di Bogor pada tanggal 13 September 2000. Dari saya lahir sampai sekarang saya bertempat tinggal di Bogor sehingga setiap hari saya pulang pergi ke UI menaiki kereta commuter line. Sebelumnya saya belum memiliki basic dalam bahasa pemrograman. Diharapkan dengan mengikuti mata kuliah Metode Numerikal ini, saya dapat lebih mengerti dan memahami pemrograman.

Pertemuan ke-1 (7 Februari 2020)

Pertemuan pertama mata kuliah Metode Numerik dilaksanakan pada tanggal 7 Februari 2020. Dosen pengampu mata kuliah ini adalah Bapak Dr. Ahmad Indra Siswantara. Beliau pertama memperkenalkan diri dan juga memperkenalkan basic dalam mempelajari Metode Numerik. Beliau memberitahu kepada mahasiswa bahwa Metode Numerik sangat penting dalam melakukan sesuatu yang dapat ditunjang oleh Metode Numerik.

Tugas I

Mahasiswa diminta mencari solusi dari soal matematika baik secara manual maupun menggunakan metode numerik. soalnya sebagai berikut.

alt text

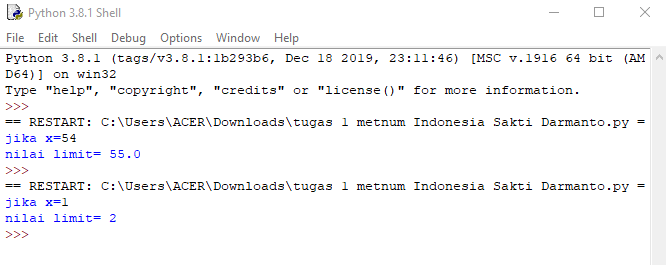
jika x=1, solusi yang didapat dengan cara manual berupa:

alt text

alt text

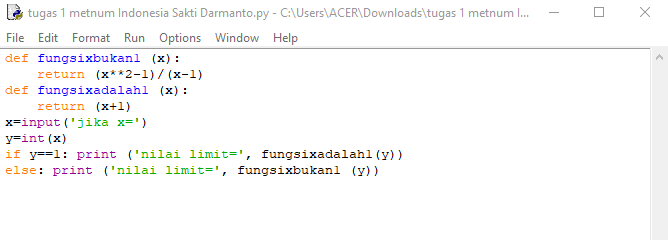
jika dilakukan dengan menggunakan Python berupa:

alt text

jika algoritmanya telah dimasukkan, maka langkah selanjutnya yaitu melakukan run module sehingga hasil dari fungsi soal tersebut akan didapatkan

alt text

Pertemuan Ke-2 (14 Februari 2020)

ilmu metode numerik sangat penting untuk dipelajari terutama bagi engineer. Supaya dapat memahami konsep yang ada, baik untuk Metode Numerik maupun cabang ilmu lain, kita harus membalikkan sifat KEM (ketidaktahuan, Egois, dan Malas) pada diri masing-masing. Adanya kesinambungan antara ilmu-ilmu lain seperti kalkulus dan aljabar linear dengan ilmu metode numerik. Masalah-masalah yang ada dalam lingkup ilmu diferensial tersebut dapat ditemukan solusinya dengan manual, namun demi tercapainya penyelesaian solusi secara lebih cepat tanpa error maka muncullah ilmu metode numerik.

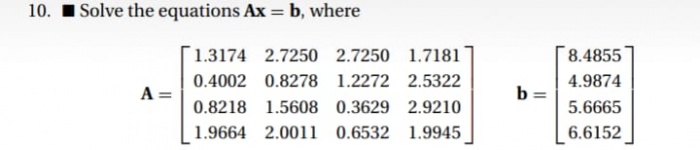
untuk mengetahui cara penyelesaian solusi dari problem tersebut, pada buku Numerical Methods in Engineering with Python3 terdapat soal-soal untuk latihan. Salah satu permasalahan yang saya baca di buku ini yaitu pada problem set 2.2 halaman 79 nomor 10 Di soal tersebut diminta untuk mencari equations Ax = B pada bentuk aljabar linear. Soal tersebut membuat saya tertarik karena angka yang ada pada matriks A dan matriks B sangat rumit, yaitu berupa desimal dengan beberapa angka di belakang koma. Matriks A diketahui berupa matriks ordo 4x4. Matriks b diketahui berupa matriks ordo 4x1.

alt text

Saya ingin mengetahui bagaimana mekanisme penyelesaiannya sehingga angka-angka yang rumit tersebut dapat terselesaikan.

Persamaan empiris adalah sebuah pola hubungan antara satu parameter dengan parameter lain, seperti variabel terikat dengan variabel bebas. Contohnya seperti hambatan kapal merupakan fungsi dari kelajuannya.

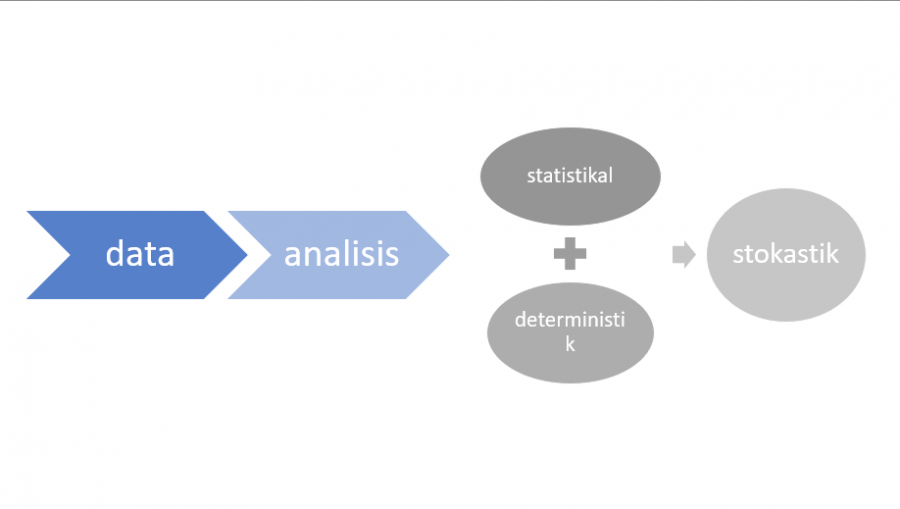
data -> analisis -> statistikal (data diskrit) berdasarkan pengukuran aktual dan deterministik (persamaan diferensial) berdasarkan hukum-hukum ideal. Analisis statistikal dan deterministik bila digabung akan menjadi stokastik. Permasalahan terbagi menjadi 2 yaitu initial value problem dan boundary value problem.

Tugas II

1. menyelesaikan soal yang telah dipilih saat pertemuan kedua, baik dengan cara manual maupun dengan menggunakan metode numerik

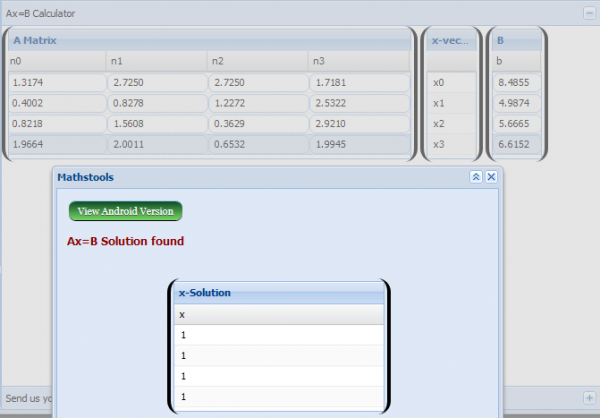
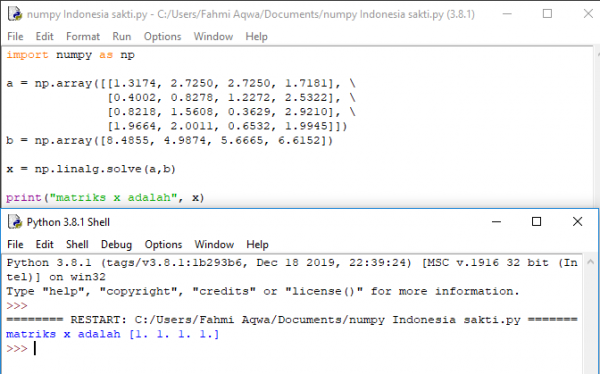
  a. metode manual didapat solusi AX=B berupa

alt text

  b. metode numerik dengan menggunakan Python seperti berikut:

alt text

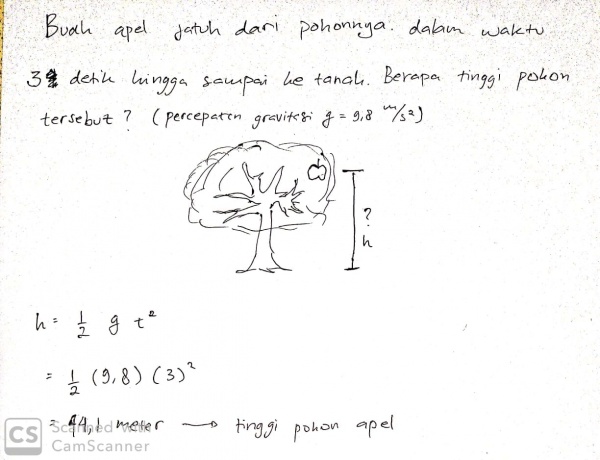
2. menyelesaikan soal di bab 7 mengenai gerak jatuh bebas

  a. metode manual didapat solusi pada permasalahan gerak jatuh bebas

alt text

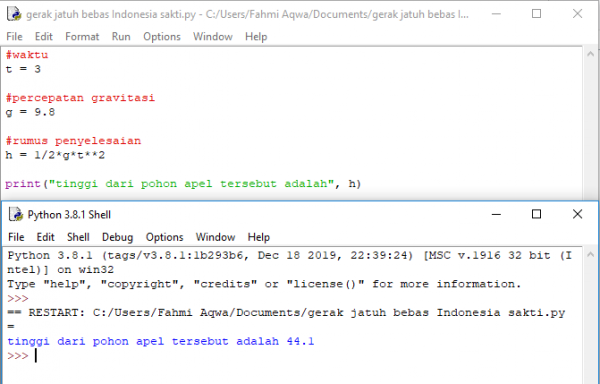
  b metode numerik menggunakan Python seperti berikut:

alt text

Presentasi Progress Belajar

alt text

alt text

alt text

alt text

pertemuan ke-3 (21 Februari 2020)

Sebuah pembelajaran bukan sekadar memahami dengan baik dan cepat, yang terpenting adalah berprogress. Hal inilah yang mendasari Bapak Ahmad Indra dengan meminta mahasiswa untuk membuat presentasi mengenai progress belajar yang telah dijalani masing-masing individu. Setelah itu, mahasiswa diminta untuk melakukan sharing mengenai progress belajarnya masing-masing. progress sama halnya dengan makna yang terkandung dalam rumus y=mx+c. yang mana bila m-nya positif maka grafik yang terbentuk akan naik. bila m-nya 0 maka grafik yang terbentuk berupa garis lurus konstan. bila m-nya negatif maka grafik yang terbentuk akan turun.

pertemuan kali juga membahas mengenai Pemodelan. pada teknik perkapalan, pemodelan bisa diterapkan CFD (Computating Fluid Dynamic). pemodelan merupakan anggapan atau pendekatan mengenai suatu kasus yang ingin dipecahkan. Sesuai dengan maknanya, pemodelan hanya melakukan pendekatan saja, sehingga pemodelan tidak akan sama dan sesuai dengan kondisi aktual.

Pemodelan ini didapat atas 3 dasar rumus pada dunia teknik, yaitu

  1. konservasi massa, dM/dt=0

  2. konservasi momentum, -> ordinary differential contohnya dv/dt
                          -> partial differential contohnya ∂v/∂t 

  3. konservasi energi, persamaan energy balance

laporan asistensi 25 Februari 2020

alt text

alt text

alt text

alt text

Tugas 3

Diketahui

alt text

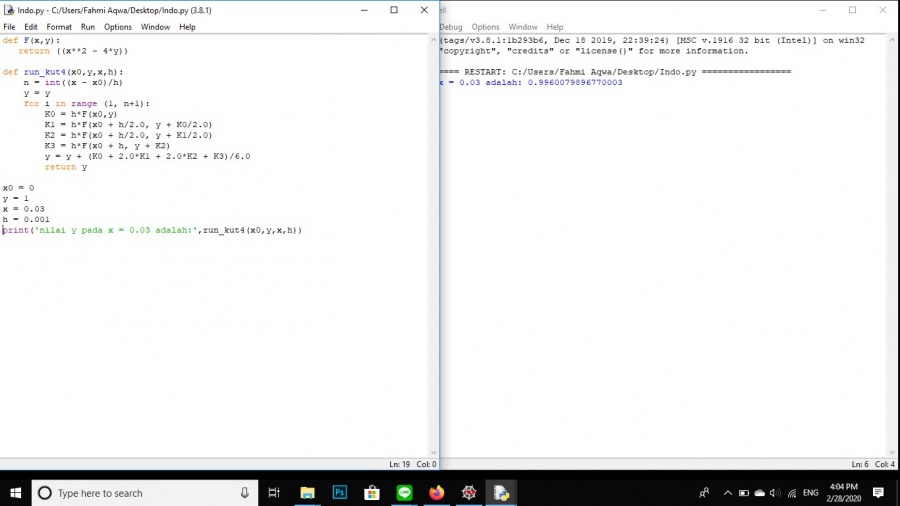
Penyelesaian menggunakan aplikasi Python

alt text

Dengan menjalankan module run kut4, problem solving untuk masalah tersebut menjadi lebih tepat, cepat, dan lebih presisi dibandingkan dengan metode manual

Laporan Progress Belajar 2

alt text

alt text

alt text

alt text

alt text

Tugas 4

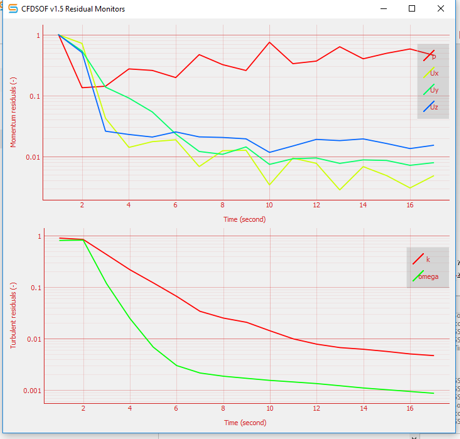
pada tugas ini, mahasiswa diminta untuk mendapatkan regresi linear dari data yang didapat dari hasil penggunaan software CDFSOFT.

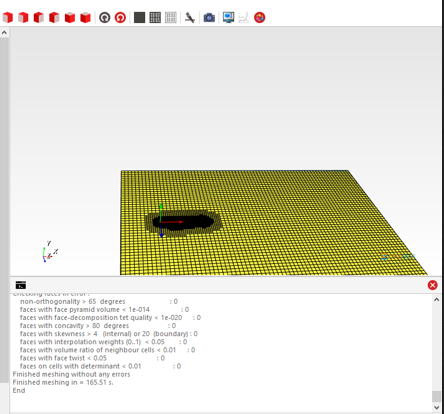
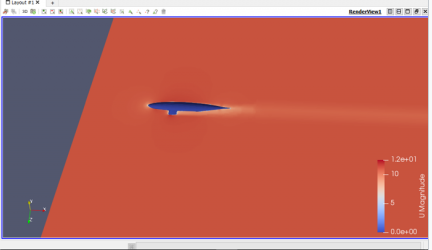
1. langkah 1 CDFSOFT digunakan untuk menangani kasus-kasus yang terkait dengan fluida. Dalam kasus ini, fenomena yang dipilih adalah kasus yang dialami kapal selam.

alt text

variabel yang diubah pada kasus ini adalah kecepatannya. Kecepatan yang digunakan di antaranya 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, dan 20. Dengan begitu, data yang didapat berupa nilai drag dari kapal selam.

alt text

2. langkah 2 dilanjut dengan menggunakan Paraview. Pada bagian ini akan dihitung Pstatic dan perhitungan drag.

bila perhitungan selesai, selanjutnya diterapkan pada kapal selam sehingga mendapat nilai drag.

alt text

alt text

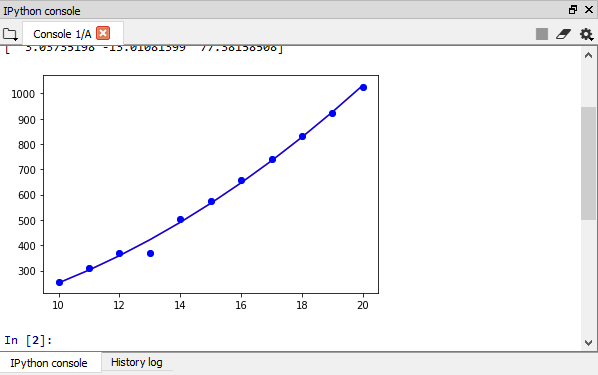
3. langkah 3 dilanjut dengan menggunakan Python. Hal ini dilakukan untuk mendapat regresi linear. Dengan memasukkan module untuk membuat regresi, kemudian memasukkan nilai x sebagai variabel kecepatan dan nilai y sebagai nilai drag, maka akan didapatkan regresi linearnya.

alt text

didapat grafik antar kecepatan dengan nilai drag

alt text

laporan asistensi ke-3 (10 maret 2020)

alt text

alt text

alt text

alt text

alt text

Tugas 5

1. boundary value problem

data didapatkan dari penggunaan CDFSOFT kapal selam pada kecepatan 18, 19, dan 20

alt text

alt text

lalu kemudian setelah mendapat nilai drag, data tersebut dimasukkan ke dalam operasi di Python

alt text

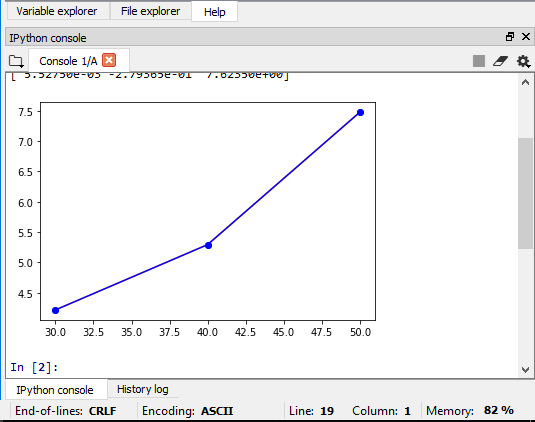
lalu akan didapat regresi linearnya

alt text

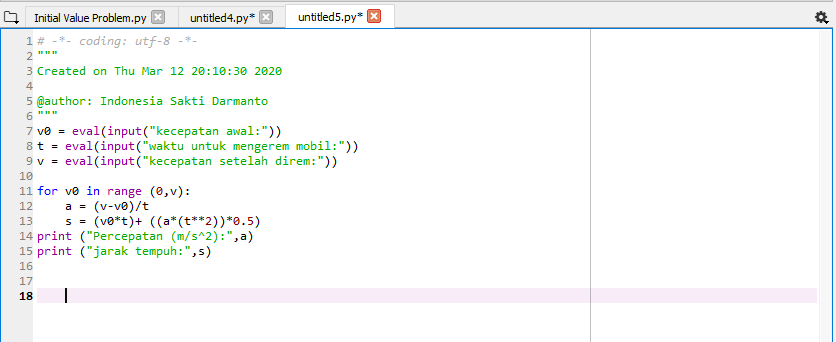
2. Initial value problem

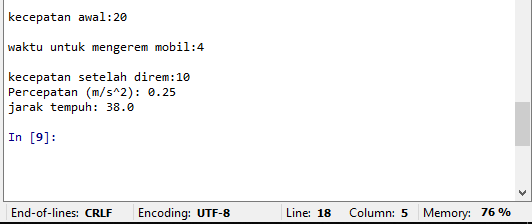
Bentuk permasalahannya berupa mobil dengan kecepatan awal v0, mengerem selama jangka waktu t sampai kecepatannya menjadi v

alt text

Mencari jarak yang ditempuh s selama mengerem

alt text

Pertemuan Ke-6 (13 Maret 2020)

Pada pertemuan kali ini, mahasiswa diajarkan mengenai optimasi oleh Bang Edo. Optimasi merupakan suatu metode untuk mendapatkan nilai optimal dari suatu fungsi yang diketahui.

Dengan optimasi, kita dapat membuat dan mengetahui hal mana yang memiliki tingkat efektif dan efisien tinggi. Cara mendapatkan nilai optimal tersebut dengan mengoptimasi fungsi objektifnya. Catatan bila fungsinya memiliki batas (constrain) maka mengoptimasinya secara berbeda.

Optimasi melalui komputasi akan mendapatkan nilai yang lebih akurat.

Tugas(6) video optimasi

alt text