Difference between revisions of "Ardhanu.adha"
Ardhanu.adha (talk | contribs) |
Ardhanu.adha (talk | contribs) |
||
| Line 280: | Line 280: | ||
[[File:Dhanu3.JPG|500px|center]] | [[File:Dhanu3.JPG|500px|center]] | ||
[[File:Dhanu4.JPG|500px|center]] | [[File:Dhanu4.JPG|500px|center]] | ||
| + | |||
| + | |||
| + | == Tugas 5 : Soal Initial Value Problem dan Boundary Value Problem == | ||
| + | |||
| + | '''Initial Value Problem''' | ||
| + | |||
| + | Diketahui aerodynamic drag force pada pesawat adalah dengan persamaan berikut | ||
| + | |||
| + | FD = av^2 e^by | ||
| + | |||
| + | v = kecepatan (m/s) | ||
| + | |||
| + | Dengan asumsi sebagai berikut : | ||
| + | |||
| + | a = 7.5 kg/m | ||
| + | |||
| + | b = 10.53 x 10^5 m^-1 | ||
| + | |||
| + | y = ketinggian (m) | ||
| + | |||
| + | Persamaan eksponensialnya dari perubahan massa jenis udara terhadap ketinggian. Persamaan diferensialnya : | ||
| + | |||
| + | my = -mg + FD | ||
| + | |||
| + | g = 9.8 m/s^2 | ||
| + | |||
| + | m = 180 ton = 180.000 kg | ||
| + | |||
| + | Jika ketinggian awal (y0) = 10km. Carilah ketinggian serta kecepatan setelah 10 detik! | ||
| + | |||
| + | |||
| + | import numpy as np | ||
| + | import math | ||
| + | from run_kut5 import * | ||
| + | from printSoln import * | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | def F(x,y): | ||
| + | F = np.zeros(2) | ||
| + | F[0] = y[1] | ||
| + | F[1] = -9.80665 + 4.167e-5 * y[1]**2 * math.exp(-10.53e-5*y[0]) | ||
| + | return F | ||
| + | |||
| + | x = 0.0 | ||
| + | xStop = 10.0 | ||
| + | y = np.array([10000, 0.0]) | ||
| + | h = 0.5 | ||
| + | freq = 1 | ||
| + | X,Y = integrate(F,x,y,xStop,h,1.0e-2) | ||
| + | printSoln(X,Y,freq) | ||
| + | plt.plot(X,Y[:,0],'o-',X,Y[:,1],'-',color='r') | ||
| + | |||
| + | plt.xlabel('Time (s)') | ||
| + | plt.ylabel('Elebation (m)') | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | input("\nPress return to exit") | ||
| + | |||
| + | '''Boundary Value Problem''' | ||
| + | |||
| + | Salah satu contoh soal Boundary Value Problem adalah Kasus Drag Kapal Selam seperti pada Tugas 4 | ||
| + | |||
| + | Diketahui hasil drag force pada CFDSOF sebagai berikut | ||
| + | |||
| + | [[File:Tabel_variasi.PNG|150px|center]] | ||
| + | |||
| + | Lalu diselesaikan dengan menggunakan aplikasi Python | ||
| + | |||
| + | [[File:Regresi_pythondanu2.PNG|600px|center]] | ||
== Pertemuan 6 == | == Pertemuan 6 == | ||
| − | + | '''Fungsi Objektif''' | |
| + | |||
| + | Dalam melakukan optimasi kita perlu mengetahui terlebih dahulu mengenai fungsi objektif | ||
| + | |||
| + | Contoh Soal: | ||
| + | |||
| + | Bambang memiliki balok kayu sepanjang 20 meter. Bambang ingin membuat pagar yang mengelilingi halaman rumahnya. Dia ingin sebisa mungkin luas halaman yang dikelilingi pagar kayu tersebut sebesar mungkin tetapi panjang pagar tersebut tidak kurang dari 8 meter.Bagaimana Bambang mengoptimasi balok kayu tersebut agar pagar yang dia inginkan tercapai? | ||
| + | |||
| + | Diketahui : | ||
| + | |||
| + | Kayu = 20 meter | ||
Luas Halaman Paling Besar | Luas Halaman Paling Besar | ||
| Line 293: | Line 372: | ||
Inequality Conseraint => P >= 8 meter | Inequality Conseraint => P >= 8 meter | ||
| + | |||
| + | |||
| + | == Tugas 6 : Optimasi Pagar Kayu == | ||
Revision as of 19:48, 19 March 2020
Contents
- 1 Tentang Saya
- 2 Tugas 1
- 3 Pertemuan Ke-2
- 4 Tugas 2
- 5 Progress Pembelajaran Metode Numerik
- 6 Pertemuan 3 : Pemodelan
- 7 Pemodelan Pegas Dengan Menggunakan Metode Runga Kutta
- 8 Laporan Asistensi 1
- 9 Laporan Asistensi 2
- 10 Tugas 4 : Regresi Hasil Perhitungan Hambatan Menggunakan CFD Dengan Variasi 10 Kecepatan
- 11 Laporan Asistensi 3
- 12 Tugas 5 : Soal Initial Value Problem dan Boundary Value Problem
- 13 Pertemuan 6
- 14 Tugas 6 : Optimasi Pagar Kayu
Tentang Saya
- Nama : Ardhanu Adha
- NPM : 1806149583
- Prodi : Teknik Perkapalan
- Angkatan : 2018
Hobi
- Memelihara hewan
- Travelling
- Membaca buku
Harapan
- Dapat merumuskan permasalahan pada bidang perkapalan dengan Metode Numerik
- Menjadi pribadi yang lebih baik setelah mempelajari Metode Numerik
- Belajar banyak hal dari kelas Metode Numerik
Tugas 1
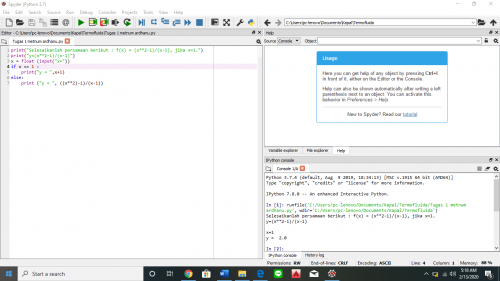
Perhitungan Menggunakan Python
Perhitungan Menggunakan Manual
f(x) = (x^2-1)/(x-1)
= (x+1)(x-1)/(x-1)
= x+1
f(1) = 1+1
= 2
Tanggapan
Menurut saya, dengan menggunakan bantuan software dan metode numerik perhitungan ataupun penyelesaian persamaan matematik yang rumit dapat diselesaikan dengan lebih mudah. Namun, apabila persamaan matematik tersebut cukup mudah (seperti contoh diatas) menurut saya tidak perlu menggunakan bantuan software.
Pertemuan Ke-2
- Tujuan Belajar Metode Numerik
1. Memahami konsep-konsep dan prinsip-prinsip metode numerik
2. Mengerti dan memahami pengaplikasian metode numerik
3. Lebih mengenal diri sendiri. Semakin mengerti apa yang kita tidak tau
- Ilmu yang kita punya adalah hanya bagaikan setetes air jika dicelupkan di samudera. Tetesan tersebut adalah air bukan minyak. Air tersebut akan menyatu dengan samudera yang luas. Ilmu yang bagaikan samudera itulah yang dimiliki oleh Tuhan Yang Maha Esa.
- Bisa menggunakan metode numerik untuk menyelesaikan berbagai persamaan kalkulus, algebra dan lain-lain.
- Cara mengatasi rasa malas adalah malu sama Tuhan yang telah memberikan berbagai nikmat kepada kita.
- Turn back KEM : Ketidaktahuan(kebodohan), Egois dan Malas
- Data => Informasi => Pengetahuan => Ilmu yang bermanfaat => Hikmah => Hidayah
Saya tertarik dengan soal no.1 halaman 126 karena materi soal tersebut selaras dalam membuat tugas linesplan kapal saya menggunakan interpolasi
Source : Numerical Methods in Engineering With Python 3 , Third Edition- Jaan Kiusalaas
Tugas 2
Metode Lagrange
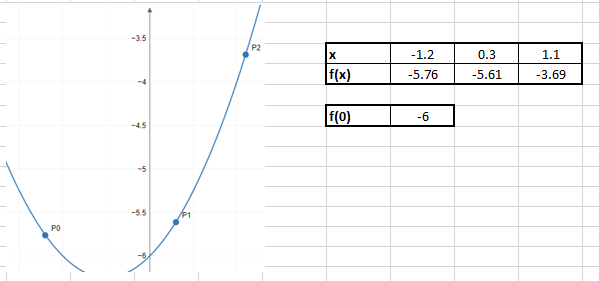
l0(x) = (x−0.3)(x−1.1)/(−1.2−0.3)(−1.2−1.1) = x2−1.4x+0.33/3.45 = 0.28985507246377x2−0.40579710144928x+0.095652173913043
l1(x) = (x+1.2)(x−1.1)/(0.3+1.2)(0.3−1.1) = x2+0.1x−1.32/−1.2 = −0.83333333333333x2−0.083333333333333x+1.1
l2(x) = (x+1.2)(x−0.3)/(1.1+1.2)(1.1−0.3) = x2+0.9x−0.36/1.84 = 0.54347826086957x2+0.48913043478261x−0.19565217391304
L(x) = −5.76(0.28985507246377x2−0.40579710144928x+0.095652173913043)−5.61(−0.83333333333333x2−0.083333333333333x+1.1)−3.69(0.54347826086957x2+0.48913043478261x−0.19565217391304)
L(x) = x2+x−6
L(0) = 0+0-6 = -6
Metode Neville
f(x) = (x-2)(x+3)
f(0) = (0-2)(0+3) = (-2)(3) = -6
Metode Excel
Initial Value Problem
Metode Manual
Metode Software
Progress Pembelajaran Metode Numerik
Pertemuan 3 : Pemodelan
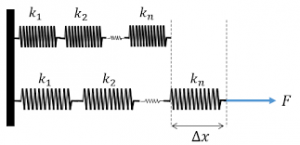
Contoh Initial Value Problem : Pegas
y = mx + c
Persitiwa pada pegas yaitu adalah osilasi. Gerak naik turun pada pegas dapat dihitung dengan frekuensi.
Dalam setiap permodelan pasti ada asumsi karena permodelan adalah pendekatan.
F = kx
k adalah koefisien material/bahan pegas tersebut
Dalam hidrodinamika kapal, kita dapat menghitung dinamika kapal dengan menggunakan software CFD.
Rumus pada dunia keteknikan sebenarnya tidak banyak namun turunannya yang banyak
Konsep Kesetimbangan
Prinsip dunia teknik:
1. Konservasi Massa
Massa itu tidak dapat diciptakan maupun dimusnahkan. Melainkan hanya bisa dikonservasikan.
dM/dt = 0 => Prinsip konservasi massa
2. Konservasi Momentum (Kesetimbangan Gaya)
sigmaF = M dv/dt = M dov/dox dx + dov/doy dy + dov/doz dz => Prinsip konservasi momentum
Perbedaan dv/dt dengan dov/dot:
dv/dt adalah turunan keseluruhan => laju perubahan total
dov/dot adalah turunan parsial => laju perubahan parsial
3. Konservasi energi
Energi tidak dapat diciptakan maupun dihilangkan melainkan hanya dapat diubah bentuknya.
dE/dt = W + Q => Prinsip konservasi energi
Pemodelan Pegas Dengan Menggunakan Metode Runga Kutta
# x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment dengan nilai h = 0.01.
x0 = 0
y = 0
h = 0.01
x = float(input("Masukkan nilai t: "))
if 0 <= x < 2:
# dydx menyatakan persamaan awal dalam soal. Persamaan diintegralkan sekali untuk menghasilkan persamaan kecepatan.
# Didapat hasil 2x^2 - 30xy karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
# P(t) dinyatakan dalam x.
def dydx(x, y):
return (2*x**2 - 30*x*y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 2:
# Ketika x >= 2, perhitungan harus diganti karena P(t) sudah konstan di angka 20 N.
def dydx(x, y):
return (8 - 30*x*y)
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
else:
print("Mohon masukkan nilai t positif.")
Laporan Asistensi 1
Laporan Asistensi 2
Berikut adalah laporan hasil asistensi metode numerik pada Selasa,3 Maret 2020 yang saya ikuti.
Tugas 4 : Regresi Hasil Perhitungan Hambatan Menggunakan CFD Dengan Variasi 10 Kecepatan
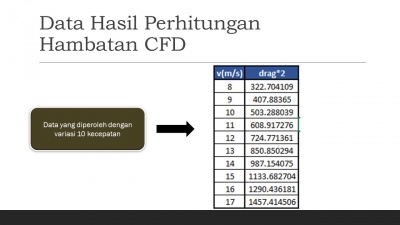
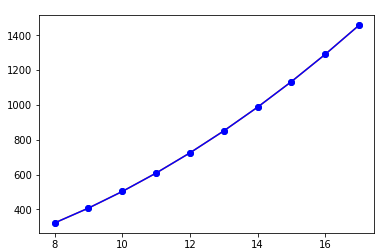
Saya mengambil 10 variasi kecepatan kapal yaitu 8,9,10,11,12,13,14,15,16,17 m/s.
Lalu dengan memasukkan variasi kecepatan tersebut pada software CFD maka didapatkan data hambatan(drag) kapal dengan hasil sebagai berikut
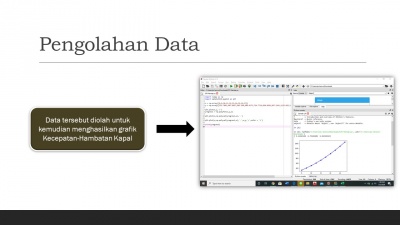
Kemudian saya menggunakan aplikasi python untuk mengoding agar mendapatkan grafik regresi yang diinginkan.
Dengan x adalah variasi kecepatan dan y adalah hambatan kapal dikali 2
Sehingga didapatkan Grafik Kecepatan-Hambatan sebagai berikut
Laporan Asistensi 3
Tugas 5 : Soal Initial Value Problem dan Boundary Value Problem
Initial Value Problem
Diketahui aerodynamic drag force pada pesawat adalah dengan persamaan berikut
FD = av^2 e^by
v = kecepatan (m/s)
Dengan asumsi sebagai berikut :
a = 7.5 kg/m
b = 10.53 x 10^5 m^-1
y = ketinggian (m)
Persamaan eksponensialnya dari perubahan massa jenis udara terhadap ketinggian. Persamaan diferensialnya :
my = -mg + FD
g = 9.8 m/s^2
m = 180 ton = 180.000 kg
Jika ketinggian awal (y0) = 10km. Carilah ketinggian serta kecepatan setelah 10 detik!
import numpy as np
import math
from run_kut5 import *
from printSoln import *
import matplotlib.pyplot as plt
def F(x,y): F = np.zeros(2) F[0] = y[1] F[1] = -9.80665 + 4.167e-5 * y[1]**2 * math.exp(-10.53e-5*y[0]) return F
x = 0.0 xStop = 10.0 y = np.array([10000, 0.0]) h = 0.5 freq = 1 X,Y = integrate(F,x,y,xStop,h,1.0e-2) printSoln(X,Y,freq) plt.plot(X,Y[:,0],'o-',X,Y[:,1],'-',color='r')
plt.xlabel('Time (s)')
plt.ylabel('Elebation (m)')
plt.grid(True)
plt.show()
input("\nPress return to exit")
Boundary Value Problem
Salah satu contoh soal Boundary Value Problem adalah Kasus Drag Kapal Selam seperti pada Tugas 4
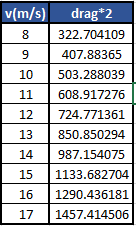
Diketahui hasil drag force pada CFDSOF sebagai berikut
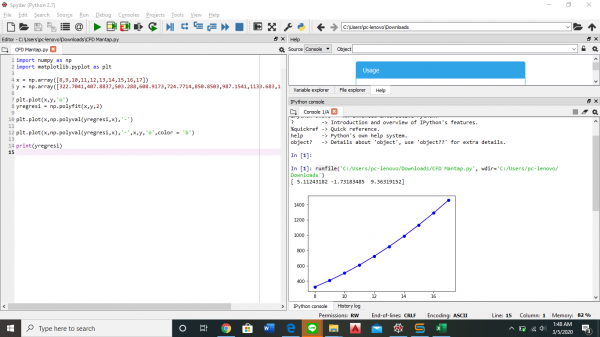
Lalu diselesaikan dengan menggunakan aplikasi Python
Pertemuan 6
Fungsi Objektif
Dalam melakukan optimasi kita perlu mengetahui terlebih dahulu mengenai fungsi objektif
Contoh Soal:
Bambang memiliki balok kayu sepanjang 20 meter. Bambang ingin membuat pagar yang mengelilingi halaman rumahnya. Dia ingin sebisa mungkin luas halaman yang dikelilingi pagar kayu tersebut sebesar mungkin tetapi panjang pagar tersebut tidak kurang dari 8 meter.Bagaimana Bambang mengoptimasi balok kayu tersebut agar pagar yang dia inginkan tercapai?
Diketahui :
Kayu = 20 meter
Luas Halaman Paling Besar
Fungsi Objective => Luas Halaman = A = P x L
Equality Conseraint => Keliling = P + P + L + L = 20
Inequality Conseraint => P >= 8 meter