Ardy.lefran

Profile

Source: Personal documentation

Fullname: Ardy Lefran Lololau

Nickname: Ardy

Place, Date of Birth: Kupang, August 20th 1997

NPM: 1906433556

Department/Specialization: Mechanical Engineering / Design and Product Manufacturing

Promotor: Prof. Dr. Ir. Tresna Priyana Soemardi, M.Si., S.E. (TPS)

Research interest: Composite materials

Phone: +62 822 47033 572

E-mail: ardy.lefran@ui.ac.id ; ardylefranlololau@gmail.com

1. Engineering Computation

Courses name: Engineering Computation

Courses code: ENME802004

Lecturer: Dr. Ir. Ahmad Indra Siswantara (Mr. DAI)

Weighting: 2 SKS

Term: 2

1.1. First Class (Feb 3rd 2020)

A. What is engineering computation?

In my opinion, engineering computation is an engineering science that uses computer assistance to help an engineer to process a data which complex, repeated, and consists in large numbers, to reduce human error and make time and cost more efficient in solving an engineering matter.

B. What is the objective of this course?

1. To understand the concepts and principals in engineering computation. The terms (iteration, validation, verification, regression, error, convergent, etc.), function, used numerical method, etc.

2. To be able to apply the understanding of engineering computation in a real engineering matter, mainly mechanical. Able to identify a problem, translate it into a programming language (INPUT), use a software on a computer to cultivate it (PROCESS), get a result (OUTPUT) and match it with existing theory.

3. To be a media to know ourselves. Able to identify ourselves (am I confirm with the standard?) in a certain way to get a better understanding in capability of skills, value, and knowledge, especially at engineering computation.

C. Engineering computation capabilities (Muhasabah)

My capability at engineering computation is superficial. I am not really used to engineering computation. My only decent work with engineering computation was the work on my final project at the Bachelor degree, which is using only Ms. Excel to calculate and analyze the amount of dissipation energy that occurs in a composite specimen during a dynamic-tensile test. I am looking forward to learning a lot in this course to improve my skills, value, and knowledge. Credits to Mr. DAI for letting me and my fellow student-friends to have an opportunity to join in this course, and for the insight given to us, hopefully, it will be useful.

1.2. Second Class (Feb 10th 2020)

A. Class Resume

In this class, we have been taught again about fundamental things in life. Mr. DAI said that we, as a millennial generation, should not forget nature. We have to study independently like Khairul, a person who has no formal education background but can make and fly his plane. We have to learn from experience because, as the proverb said, the experience is an excellent teacher.

We also have been taught what analysis is. According to the class’s consensus, analysis is an investigation process that includes some activities to solve problems by being reviewed as well as possible using structured thinking. Meanwhile, according to Mr. DAI, analysis is a rational way of the thinking process to gain a matter-solving procedure.

B. Bachelor thesis synopsis

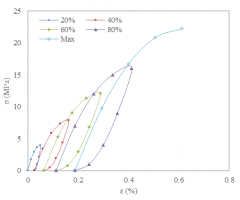
My bachelor thesis entitled “Determination of Energy Dissipation and Thermal Behavior of Lontar Fiber Composite under Dynamic Tensile Test”. The purpose of this research was to determine the energy dissipation of Lontar (Borassus Flabellifer) fiber composite by its mechanical behavior and validate it by its thermal response. The material used in this study is an open-hole rectangular polymer composite specimen reinforced by Lontar fiber of 5 cm length and random orientation against each other and fabricated by hand lay-up method. The composite specimen contains 30% of nominal fiber volume, which has been treated using 5% of NaOH for 1 hour, and the rest is Polyesters resin.

Source: Personal documentation

The test was carried out according to the American Society for Testing and Materials (ASTM) D5766 testing standards in 2 (two) phases. The first phase is a tensile test under static load to determine the value of Ultimate Tensile Strength (UTS). The second phase is a tensile test under dynamic loads to have the hysteresis curve of each loading-unloading percentage of UTS. In this experiment, a load of 20%, 40%, 60%, 80% of the UTS has applied and then continued until the specimen failed, while thermocouple is used to record temperature evolution on specimen surface around the hole area.

The results of this study showed that the highest energy dissipation at the 80% loading level by mean of 0.215309063 J/cm3, while the lowest dissipation energy is at the 20% loading level by mean of 0.001430625 J/cm3. The amount of dissipation energy at each loading level would affect the mechanical strength of the composite specimen and each type of damage propagation that occurs in material. The area of the hysteresis loop must be significantly enlarged before the final damage occurs, indicating that more energy is absorbed before the damage finally occurs. The relationship of energy dissipation and temperature changes through thermocouples can be caused by energy dissipation from materials that might cause microscopic damage.

C. Bachelor thesis project with engineering computation

My intention is to implement engineering computation to make a failure model based on the stress distribution of a random-oriented fiber composite, which is i found very hard since the data will spread stochastically. The presence of an open-hole in the middle of the specimen was made the stress concentration localize at it. So I want to make a model of stress concentration factor at the open-hole area. My alternative eagerness is to create a deterministic failure model based on the temperature evolution behavior near the open-hole so that we can predict when the failure is about to occur based on the experimental data. I still have not determined yet which numerical analysis I will use since I am not really used to engineering computation. I will discuss any further with Mr. DAI to guide me for this project.

1.3. Third Class (Feb 17th 2020)

A. PPT of Project Synopsis

• 
• 
• 
• 
• 

B. Class Resume

In this class, Mr. DAI tells us to against the nescience, selfishness, laziness. Just like the Police of RI with their slogan "Turn back Crime". In my opinion, one of the ways to against the previous matter is to think critically.

We found a y as x function, as follow: y = (x^2-1)/(x-1). With x = 1, how was the y? If we put the direct substitution into the function, it will conclude y = undefined (0/0). If we change x to 2, 3, 4, and so on, it will culminate y as a real number. So what is the problem?

As human beings, we have to think critically to solve the problem. Back in the math lecture, we have been taught about the limit. In mathematics, a limit is a value that a function (or sequence) "approaches" as the input (or index) "approaches" some value. Thus, if we use limit into the function before, we can see that:

lim┬(x-1)⁡〖(x^2-1)/(x-1)= ((x+1)(x-1))/((x-1))=x+1=1+1 ≈2〗

1.4. Fourth Class (Feb 24th 2020)

A. PPT of Project Modelling

• 
• 
• 
• 
• 
• 
• 
• 

B. Quiz

• 
• 

C. Class Resume

FINITE ELEMENT, FINITE DIFFERENCE, AND FINITE VOLUME

The finite-element method is a computational method that subdivides a CAD model into tiny but finite-sized elements of geometrically simple shapes. The next step is to take a system of field equations, mathematically represented by partial differential equations (PDEs) that describe the physics you are interested in, and formulate these equations for each element. This is handled by approximating the fields within each element as a simple function, such as a linear or quadratic polynomial, with a finite number of degrees of freedom (DOFs). When the contributions from all elements are assembled, you end up with an extensive sparse matrix equation system that can be solved by any of several well-known sparse matrix solvers. The type of solver used depends on the original physics since each sort of physics gives its unique imprint on the structure of the matrix. To speed things up, this structure is exploited by using a tailored numerical method.

The finite-difference method is the most direct approach to discretizing partial differential equations. You consider a point in space where you take the continuum representation of the equations and replace it with a set of discrete equations, called finite-difference equations. The finite-difference method is typically defined on a regular grid, and this fact can be used for very efficient solution methods. The method is therefore not usually used for irregular CAD geometries, but more often for rectangular or block-shaped models.

The finite-volume method is similar to the finite-element method in that the CAD model is first divided into tiny but finite-sized elements of geometrically simple shapes. The finite-volume method is based on the fact that many physical laws are conservation laws—what goes into one cell on one side needs to leave the same cell on another side. Following this idea, you end up with a formulation that consists of flux conservation equations defined in an averaged sense over the cells.

1.5. Fifth Class (Mar 2nd 2020)

A. Extended Abstract

My bachelor thesis entitled “Determination of Energy Dissipation and Thermal Behavior of Lontar Fiber Composite under Dynamic Tensile Test”. The purpose of this research was to determine the energy dissipation of Lontar (Borassus Flabellifer) fiber composite by its mechanical behavior and validate it by its thermal response. The material used in this study is an open-hole rectangular polymer composite specimen reinforced by Lontar fiber of 5 cm length and random orientation against each other and fabricated by hand lay-up method. The composite specimen contains 30% of nominal fiber volume, which has been treated using 5% of NaOH for 1 hour, and the rest is Polyesters resin. The test was carried out according to the American Society for Testing and Materials (ASTM) D5766 testing standards in 2 (two) phases. The first phase is a tensile test under static load to determine the value of Ultimate Tensile Strength (UTS). The second phase is a tensile test under dynamic loads to have the hysteresis curve of each loading-unloading percentage of UTS. In this experiment, a load of 20%, 40%, 60%, 80% of the UTS has applied and then continued until the specimen failed, while thermocouple is used to record temperature evolution on specimen surface around the hole area. The results of this study showed that the highest energy dissipation at the 80% loading level by mean of 0.215309063 J/cm3, while the lowest dissipation energy is at the 20% loading level by mean of 0.001430625 J/cm3. The amount of dissipation energy at each loading level would affect the mechanical strength of the composite specimen and each type of damage propagation that occurs in material. The area of the hysteresis loop must be significantly enlarged before the final damage occurs, indicating that more energy is absorbed before the damage finally occurs. The relationship of energy dissipation and temperature changes through thermocouples can be caused by energy dissipation from materials that might cause microscopic damage. As an extended work from this study, I want to make a model of stress concentration factor at the open-hole area on a simulation-based review to compare both analytical and simulation trends using finite element simulation on ANSYS. The expected findings is the comparison chart of the stress concentration factor at the open-hole area between analytical and simulation work.