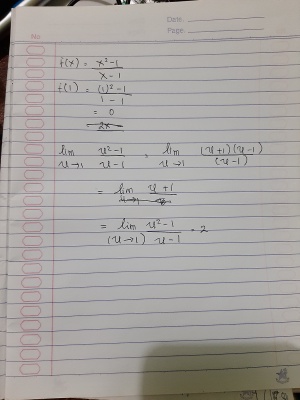Difference between revisions of "Vita Puspita"
Vita.puspita (talk | contribs) (→Tugas 2.1) |
Vita.puspita (talk | contribs) |
||
| Line 49: | Line 49: | ||
[[File:mnt5.png|400px]] | [[File:mnt5.png|400px]] | ||
[[File:mnt6.png|400px]] | [[File:mnt6.png|400px]] | ||
| + | |||
| + | == Runge-kutta sebagai alternatif perhitungan == | ||
| + | |||
| + | '''Pemodelan Pegas dengan Menggunakan Metode Runga Kutta''' | ||
| + | |||
| + | X0 dan y merupakan increment dengan nilai h = 0,01 | ||
| + | |||
| + | X0= 0 | ||
| + | Y= 0 | ||
| + | H= 0,01 | ||
| + | X= float (input(“Masukan nilai t:”)) if 0<= X <2: | ||
| + | #dydx menyatakan persamaan awal dalam soal. Persamaan diintegralkan untuk mendapatkan kecepatan. | ||
| + | #Didapatkan hasil 2x^2-30*x*y , karena menggunakan massa = 2,5 kg dan konstatnta pegas k = 75N/m | ||
| + | #P(t) dinyatakan dalam x. | ||
| + | Def dydx(x,y): | ||
| + | #P(t) dinyatakan dalam x,def dydx (x,y): | ||
| + | Return (2*x**2-30*x*y) | ||
| + | |||
| + | Merupakan implementasi perhitungan Range-kutta , def Rungekutta(x0, y0, x, h): | ||
| + | |||
| + | n = (int) ((x-x0)/(h) | ||
| + | y = y0 | ||
| + | |||
| + | k1 = h*dydx(x0,y) | ||
| + | k2 = h * dydx (x0 + 0,5 * h,y +0,5*1) | ||
| + | k3 = h* dydx (x0 + 0,5 *h, y + 0,5*k2) | ||
| + | k4 = h* dydx (x0+h, y +k3) | ||
| + | |||
| + | y= y+(1,0/6,0)*(k1 + 2 * k2 +2 *k3) | ||
| + | |||
| + | Mengikuti persamaan dengan memasukan nilai positif. | ||
| + | |||
| + | == Laporan 2 == | ||
| + | |||
| + | |||
| + | [[File:mtk1.png|400px]] | ||
| + | [[File:mtk2.png|400px]] | ||
| + | [[File:mtk3.png|400px]] | ||
| + | [[File:mtk4.png|400px]] | ||
Revision as of 22:47, 5 March 2020
Contents
Vita Puspita
Lahir di Jakarta, 13 Mei 2000, menyukai menonton film dan tidur. Berkuliah FTUI
Mengenal Programming
Saya belajar programming, dari seorang mahasiswa fasilkom UI menegnai pembuatan website. Di Bidang Perkapalan, penggunaan Programming berlaku dari perancangan hingga mencari kegagalan dalam material beserta optimasi penggunaan energi di kapal.
Tugas 1
Cara Manual
Menggunakan perhitungan manual, dengan menyelesaikan masalah dengan penggunaan limit. Hasil yang didapatkan saat diawal adalah 0, yang dimana tidak terdefinisi. Ketika dengan penggunaan limit, mendapatkan hasil f(x)=2
Cara Phython
Saya baru mencoba phython pertama kali, dengan menggunakan perhitunga komputasi. Perhitungan yang biasa dilakukan jauh lebih singkat dan cepat. Tahapan 1: membuat file baru, kemudian mulai mencoba membuat command Tahapan 2: membuka phython shell, agar command yang sudah kita rancag dari awal akan terkomputasi secara otomatis dengan hasil yang sesuai
Tugas 2.1
Apa saja yang dipelajari di Metode Numerik?
Banyak hal yang sudah dipelajari di Metode Numerik. Metode Numerik merupakan sebuah mata kuliah yang mengenalkan dasar programming until bidding keteknikan.
Tugas 3
Konservasi Momentum Pegas
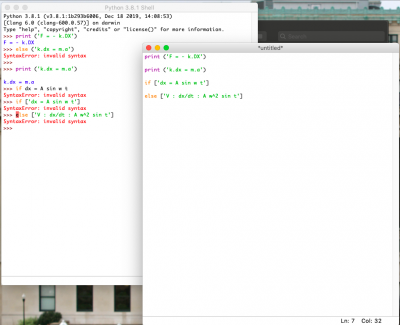
Hari Selasa kemarin saya mempelajari tentang Konservasi momentum pegas dengan cara python
Runge-kutta sebagai alternatif perhitungan
Pemodelan Pegas dengan Menggunakan Metode Runga Kutta
X0 dan y merupakan increment dengan nilai h = 0,01
X0= 0 Y= 0 H= 0,01 X= float (input(“Masukan nilai t:”)) if 0<= X <2:
- dydx menyatakan persamaan awal dalam soal. Persamaan diintegralkan untuk mendapatkan kecepatan.
- Didapatkan hasil 2x^2-30*x*y , karena menggunakan massa = 2,5 kg dan konstatnta pegas k = 75N/m
- P(t) dinyatakan dalam x.
Def dydx(x,y):
- P(t) dinyatakan dalam x,def dydx (x,y):
Return (2*x**2-30*x*y)
Merupakan implementasi perhitungan Range-kutta , def Rungekutta(x0, y0, x, h):
n = (int) ((x-x0)/(h) y = y0
k1 = h*dydx(x0,y) k2 = h * dydx (x0 + 0,5 * h,y +0,5*1) k3 = h* dydx (x0 + 0,5 *h, y + 0,5*k2) k4 = h* dydx (x0+h, y +k3)
y= y+(1,0/6,0)*(k1 + 2 * k2 +2 *k3)
Mengikuti persamaan dengan memasukan nilai positif.