Difference between revisions of "Pertemuan 2 Fadillah Nurrani"
| Line 11: | Line 11: | ||
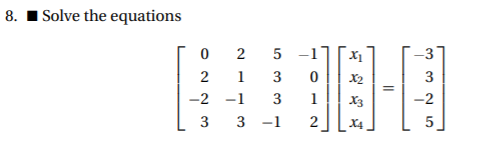
Saya mencoba mengerjakan soal diatas menggunakan metode Gauss-Jordan karena menurut saya itu yang paling mudah. | Saya mencoba mengerjakan soal diatas menggunakan metode Gauss-Jordan karena menurut saya itu yang paling mudah. | ||
Menggunakan aplikasi python, didapatkan hasil sebagai berikut: | Menggunakan aplikasi python, didapatkan hasil sebagai berikut: | ||
| − | from numpy import linalg | + | |
| − | import numpy as np | + | -from numpy import linalg |
| − | b1 = [0,2,5,-1] | + | -import numpy as np |
| − | b2 = [2,1,3,0] | + | -b1 = [0,2,5,-1] |
| − | b3 = [-2,-1,3,1] | + | -b2 = [2,1,3,0] |
| − | b4 = [3,3,-1,2] | + | -b3 = [-2,-1,3,1] |
| − | nmat = np.array ([b1,b2,b3,b4]) | + | -b4 = [3,3,-1,2] |
| − | print ("Matriks A adalah :") | + | -nmat = np.array ([b1,b2,b3,b4]) |
| − | print (nmat) | + | -print ("Matriks A adalah :") |
| − | b1 = [-3] | + | -print (nmat) |
| − | b2 = [3] | + | -b1 = [-3] |
| − | b3 = [-2] | + | -b2 = [3] |
| − | b4 = [5] | + | -b3 = [-2] |
| − | cons = np.array ([b1,b2,b3,b4]) | + | -b4 = [5] |
| − | print ("Matriks b adalah :") | + | -cons = np.array ([b1,b2,b3,b4]) |
| − | print (cons) | + | -print ("Matriks b adalah :") |
| − | jawab = linalg.solve (nmat,cons) | + | -print (cons) |
| − | x1val = int(jawab[0]) | + | -jawab = linalg.solve (nmat,cons) |
| − | x2val = int(jawab[1]) | + | -x1val = int(jawab[0]) |
| − | x3val = int(jawab[2]) | + | -x2val = int(jawab[1]) |
| − | x4val = int(jawab[3]) | + | -x3val = int(jawab[2]) |
| − | print ("Hasil X untuk matkris AX=b adalah :") | + | -x4val = int(jawab[3]) |
| − | print ("x1= ",x1val) | + | -print ("Hasil X untuk matkris AX=b adalah :") |
| − | print ("x2= ",x2val) | + | -print ("x1= ",x1val) |
| − | print ("x3= ",x3val) | + | -print ("x2= ",x2val) |
| − | print ("x4= ",x4val) | + | -print ("x3= ",x3val) |
| + | -print ("x4= ",x4val) | ||
| + | |||
[[File:Yo.PNG]] | [[File:Yo.PNG]] | ||
Revision as of 14:38, 20 February 2020
Pak Dai menugaskan mahasiswa nya untuk memilih soal-soal pengaplikasian metode numerik yang menarik menurut kami.
Dapat disimpulkan bahwa saya tertarik pada setiap bab yg ada di buku, namun yang paling membuat saya tertarik adalah soal no 8 bab 2 dikarenakan sama seperti pelajaran Aljabar Linier yaitu Eliminasi Gauss-Jordan. Selain itu saya juga menyukai pelajaran tersebut.
Sumber: Kiusalaas, Jaan. 2013. Numerical Methods in Engineering with Python 3. Cambridge: Cambridge University Press.
Contents
Jawaban
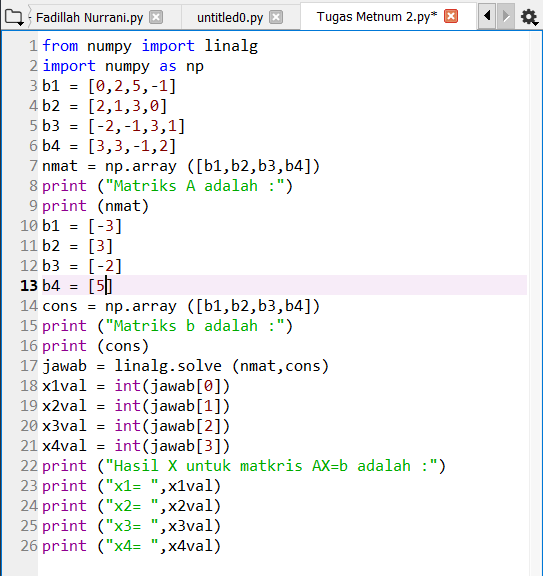
Saya mencoba mengerjakan soal diatas menggunakan metode Gauss-Jordan karena menurut saya itu yang paling mudah. Menggunakan aplikasi python, didapatkan hasil sebagai berikut:
-from numpy import linalg -import numpy as np -b1 = [0,2,5,-1] -b2 = [2,1,3,0] -b3 = [-2,-1,3,1] -b4 = [3,3,-1,2] -nmat = np.array ([b1,b2,b3,b4]) -print ("Matriks A adalah :") -print (nmat) -b1 = [-3] -b2 = [3] -b3 = [-2] -b4 = [5] -cons = np.array ([b1,b2,b3,b4]) -print ("Matriks b adalah :") -print (cons) -jawab = linalg.solve (nmat,cons) -x1val = int(jawab[0]) -x2val = int(jawab[1]) -x3val = int(jawab[2]) -x4val = int(jawab[3]) -print ("Hasil X untuk matkris AX=b adalah :") -print ("x1= ",x1val) -print ("x2= ",x2val) -print ("x3= ",x3val) -print ("x4= ",x4val)
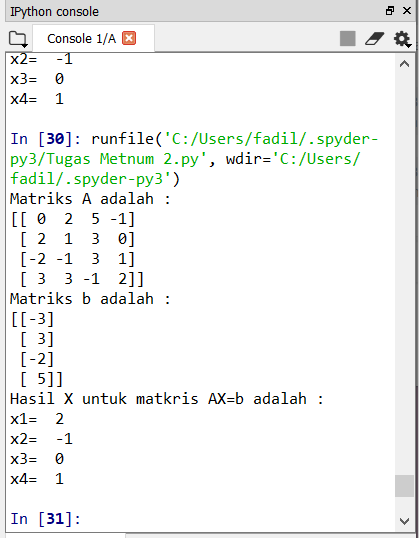
Didapatkan hasil sebagai berikut:
Bab 2
Saya tertarik saat saya melihat bab 2, saya menemukan pelajaran bahwa untuk membuat penyelesaian gauss berbentuk matriks, bisa menggunakan python dengan kode np.array. Metode dalam menyelesaikan matriks pada bab 2, bisa juga menggunakan metode Doolittle atau Metode Chooleski. Di bab 2 juga saya mendapatkan soal mengenai Gaya pada sebuah balok segitiga yang biasanya diselesaikan dengan metode manual, namun ternyata bisa diselesaikan dengan metode matriks juga. Selain itu juga, penyelesaian gauss dapat pula diselesaikan dengan metode scaled row pivoting. Untuk pengaplikasiannya ternyata banyak yang bisa diselesaikan dengan metode pada bab ini yaitu, kasus pegas dengan beban menggantung, aliran listrik, dll. Saya juga baru mengetahui ternyata matriks bisa diselesaikan dengan metode gaussSeidel.
Bab 3
Pada bab 3 ini, saya tertarik pada fakta bahwa aplikasi coding dapat membuat grafik parabola dengan pendekatan interpolasi. Jenis interpolasi nya juga beragam, seperti interpolasi polinomial yang menggunakan metode Newton dan Langrange, interpolasi dengan curve fitting, metode rasional, interpolasi dengan metode cubic spline. Selain itu bab ini juga mengajarkan untuk menghitung least square menggunakan aplikasi coding.
Bab 4 5 & 6
Pada bab 4 dijelaskan mengenai penggunaan kode untuk menyelesaikan bentuk persamaan, bab 5 mengenai turunan, dan bab 6 mengenai integral. Pada bab 4 saya tertarik pada soal saat diketahui diagram termodinamika dan efisiensinya. Selain itu juga ada mengenai momen bending untuk mencari nilai maksimum bebannya. Pada bab integral, saya tertarik pada soal mengenai kecepatan penarikan pada panahan, yang dapat dihitung menggunakan metode integral. Selain itu juga ada metode Euler, untuk mendapatkan nilai error nya. Pengaplikasian yang paling menarik untuk saya adalah msaat menghitung pegas dengan beban disamping, akrena dulu saya tidak bisa mengerjakannya dengan manual.
Bab 7 8 9 10
Materi pada bab ini saya tidak begitu mengerti mengenai apa. Namun saya tertarik pada soal di bab 7 yaitu menghitung pegas dan juga perputaran secara vertikal pada batangan. Selain itu di bab 8 saya tertarik pada soal mengenai perhitungan beam yang sama persis soalnya saat saya mengerjakan tugas Struktur Kapal 1.