Difference between revisions of "Tugas 2 Muhammad Attaritsabitsah Gibran"
(→Bantuan Program) |
(→Permasalahan 1) |
||
| Line 9: | Line 9: | ||
===Penyelesaian Manual=== | ===Penyelesaian Manual=== | ||
| − | + | Dalam menyelesaikan soal, saya menggunakan Excel sebagai alat perhitungan manual. Saya mempertimbangkan mengapa demikian karena saya rasa soal yang saya ambil tidaklah mudah. Dengan itu, saya harus mengerjakan soal tersebut agar dapat ''keep in track''. Saya telah menggunakan python awalnya, akan tetapi saya sering kehilangan arah secara tiba-tiba dikarenakan saya tidak bisa melihat hasil di interface tabel seperti Excel yang memudahkan saya membaca hasil soal. | |
| − | Dalam menyelesaikan soal, saya menggunakan Excel sebagai alat perhitungan. Saya mempertimbangkan mengapa demikian karena saya rasa soal yang saya ambil tidaklah mudah. Dengan itu, saya harus mengerjakan soal tersebut agar dapat ''keep in track''. Saya telah menggunakan python awalnya, akan tetapi saya sering kehilangan arah secara tiba-tiba dikarenakan saya tidak bisa melihat hasil di interface tabel seperti Excel yang memudahkan saya membaca hasil soal. | ||
[[File:Anotasi 2020-02-18 194252.png|700px]] | [[File:Anotasi 2020-02-18 194252.png|700px]] | ||
Sebuah lintasan satelit berbentuk elips. Maka dari itu saya menggunakan persamaan elips sebagai acuannya. Referensi yang saya ambil adalah teori hukum pertama Kepler. Telah dijelaskan bahwa lintasan memiliki nilai eksentrisitas. | Sebuah lintasan satelit berbentuk elips. Maka dari itu saya menggunakan persamaan elips sebagai acuannya. Referensi yang saya ambil adalah teori hukum pertama Kepler. Telah dijelaskan bahwa lintasan memiliki nilai eksentrisitas. | ||
| − | Saya hanya mengambil interval sudut sebesar 30 derajat. Hal tersebut sebenarnya terlalu sederhana. Seharusnya saya mendapatkan hasil di seluruh sudut. Hal tersebut dapat terealisasi bila menggunakan pemrograman python | + | Saya hanya mengambil interval sudut sebesar 30 derajat. Hal tersebut sebenarnya terlalu sederhana. Seharusnya saya mendapatkan hasil di seluruh sudut. Hal tersebut dapat terealisasi bila menggunakan pemrograman python. |
Sebuah elips memiliki persamaan | Sebuah elips memiliki persamaan | ||
| Line 30: | Line 29: | ||
Pada gambar, nilai R tertinggi ada pada sudut 60 derajat. Akan tetapi secara pasti belum tentu. Hal tersebut karena saya mengambil interval 30 derajat. Maka sudut 60 derajat hanyalah pendekatan. R tertinggi secara pasti tidak dapat ditentukan bila tidak mengambil semua data. Maka nilai R tertinggi ada disekitar 60 derajat | Pada gambar, nilai R tertinggi ada pada sudut 60 derajat. Akan tetapi secara pasti belum tentu. Hal tersebut karena saya mengambil interval 30 derajat. Maka sudut 60 derajat hanyalah pendekatan. R tertinggi secara pasti tidak dapat ditentukan bila tidak mengambil semua data. Maka nilai R tertinggi ada disekitar 60 derajat | ||
| + | |||
| + | ===Bantuan Programming=== | ||
| + | Saya menemukan bahwa soal ini lebih mudah bila dikerjakan menggunakan metode newton raphson. Karena hal tersebut yang paling mudah dan cepat. Tetapi saya harus menyiapkan modul newtonRaphson terlebih dahulu karena belum ada di library umum. Untuk menyiapkan modul newtonRaphson (spesifiknya newtonRaphson2), saya mendapat sumber dari buku acuan kelas. Berikut modul newtonRaphson2 | ||
| + | [[File:TUGAS2 MAG MODULNEWTONRAPHSON.png|700px|Modul newtonRaphson]] | ||
| + | |||
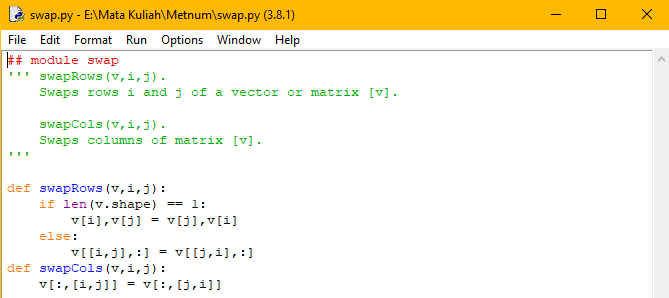
| + | modul raphson2 membutuhkan numpy, dan gaussPivot. Untuk numpy saya hanya tinggal menginstall secara biasa, karena merupakan modul yang sudah umum. Sedangkan modul gaussPivot saya harus membuat modul tersebut sendiri, lagi-lagi dari buku acuan kelas. Berikut modul gaussPivot yang juga membutuhkan modul error handling dan swap, karena berhubungan dengan matriks | ||
| + | [[File:TUGAS2 MAG MODULGAUSSPIVOT.png|700px|Modul gaussPivot]] | ||
| + | [[File:TUGAS2 MAG MODULERROR.png|Modul Error]] | ||
| + | [[File:TUGAS2 MAG MODULSWAP.png|Modul Swap]] | ||
| + | |||
| + | Setelah penyiapan modul newtonraphson, | ||
Revision as of 20:03, 19 February 2020
Permasalahan 1
Analisis Masalah
1. Satelit berevolusi di bumi, bukan di matahari. Karena bumi memiliki bentuk yang oval, maka bumi memiliki nilai eksentrisitas (e = 0,017). Maka asumsi, jalur satelit yang diambil juga memiliki nilai eksentrisitas yang sama.
2. Jarak R adalah jarak dari inti bumi ke satelit. Maka R merupakan kombinasi antara Jari-jari bumi + Ketinggian satelit dari Bumi. R merupakan koordinat polar, 
. R telah terobservasi di beberapa sudut yaitu -30, 0, dan 30 derajat. Seterusnya R di semua sudut diprediksi. Kemudian setelah itu bisa mendapatkan jarak R terendah.
3. Asumsikan nilai sudut kemiringan bumi diabaikan (yaitu sekitar 23,5 derajat) hal tersebut tidak mempengaruhi nilai
Penyelesaian Manual
Dalam menyelesaikan soal, saya menggunakan Excel sebagai alat perhitungan manual. Saya mempertimbangkan mengapa demikian karena saya rasa soal yang saya ambil tidaklah mudah. Dengan itu, saya harus mengerjakan soal tersebut agar dapat keep in track. Saya telah menggunakan python awalnya, akan tetapi saya sering kehilangan arah secara tiba-tiba dikarenakan saya tidak bisa melihat hasil di interface tabel seperti Excel yang memudahkan saya membaca hasil soal.
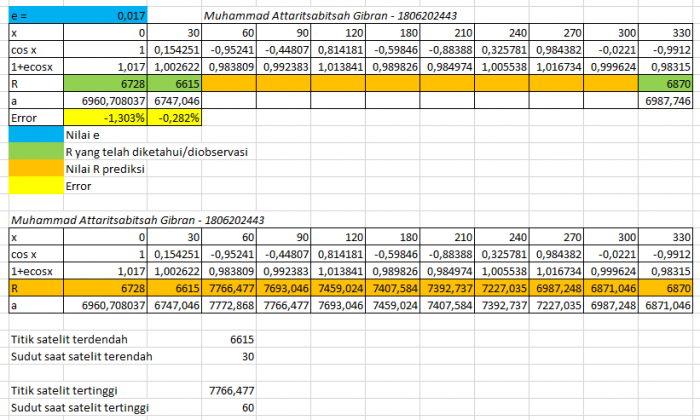
Sebuah lintasan satelit berbentuk elips. Maka dari itu saya menggunakan persamaan elips sebagai acuannya. Referensi yang saya ambil adalah teori hukum pertama Kepler. Telah dijelaskan bahwa lintasan memiliki nilai eksentrisitas.
Saya hanya mengambil interval sudut sebesar 30 derajat. Hal tersebut sebenarnya terlalu sederhana. Seharusnya saya mendapatkan hasil di seluruh sudut. Hal tersebut dapat terealisasi bila menggunakan pemrograman python.
Sebuah elips memiliki persamaan
r = a(1– e^2) / (1+ e cos φ)
a = r (1+ e cos φ)/(1– e^2)
Dimana e adalah nilai eksentrisitas. Nilai e berkisar antara 0<e<1. Jika e = 0, maka elips berbentuk lingkaran sempurna. Kemudian fungsi cos memberikan pengertian nilai yang naik turun yang digambarkan dalam grafik cos.
Saya memasukkan nilai yang telah terobservasi di baris R. Kemudian di baris R terdapat banyak sel kosong, dimaksudkan adalah nilai prediksi dari posisi R satelit.
nilai a adalah nilai R di sudut sebelumnya. Misalnya nilai a di kolom 0 derajat adalah prediksi nilai R di kolom 30 derajat sebelumnya (-30 derajat).
Pada gambar, nilai R tertinggi ada pada sudut 60 derajat. Akan tetapi secara pasti belum tentu. Hal tersebut karena saya mengambil interval 30 derajat. Maka sudut 60 derajat hanyalah pendekatan. R tertinggi secara pasti tidak dapat ditentukan bila tidak mengambil semua data. Maka nilai R tertinggi ada disekitar 60 derajat
Bantuan Programming
Saya menemukan bahwa soal ini lebih mudah bila dikerjakan menggunakan metode newton raphson. Karena hal tersebut yang paling mudah dan cepat. Tetapi saya harus menyiapkan modul newtonRaphson terlebih dahulu karena belum ada di library umum. Untuk menyiapkan modul newtonRaphson (spesifiknya newtonRaphson2), saya mendapat sumber dari buku acuan kelas. Berikut modul newtonRaphson2
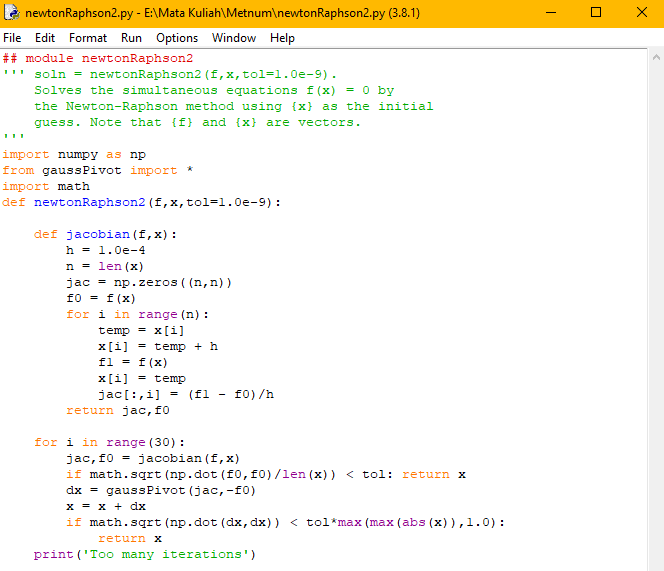
modul raphson2 membutuhkan numpy, dan gaussPivot. Untuk numpy saya hanya tinggal menginstall secara biasa, karena merupakan modul yang sudah umum. Sedangkan modul gaussPivot saya harus membuat modul tersebut sendiri, lagi-lagi dari buku acuan kelas. Berikut modul gaussPivot yang juga membutuhkan modul error handling dan swap, karena berhubungan dengan matriks
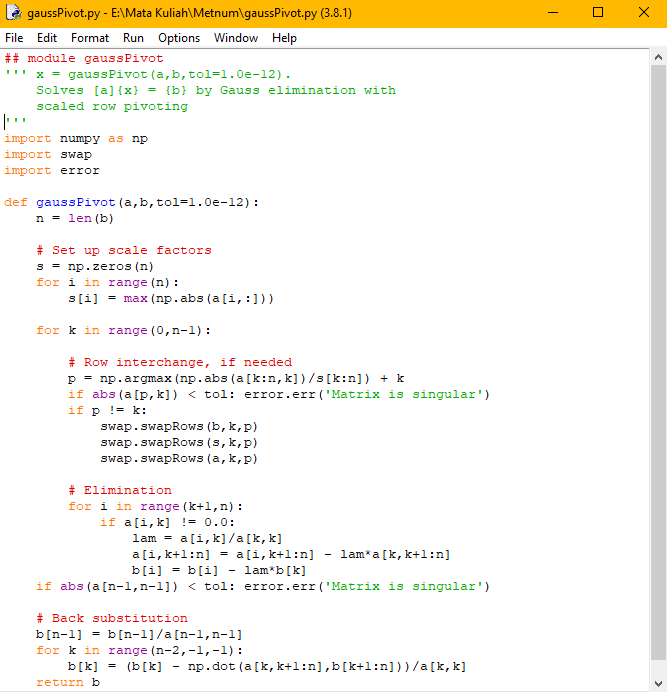
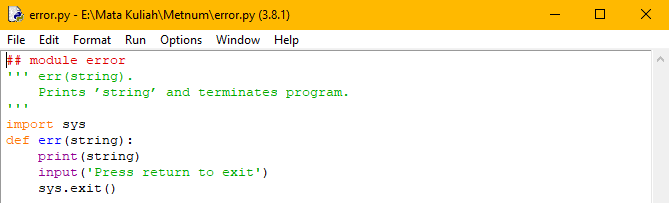
Setelah penyiapan modul newtonraphson,
