Difference between revisions of "Agis Gilang Setiawan"
(→Minggu 4) |
|||
| Line 331: | Line 331: | ||
Sebagai review | Sebagai review | ||
Presentasi kelompok yang sudah selesai | Presentasi kelompok yang sudah selesai | ||
| + | |||
| + | ===CFD CAR DRAG ANALYSIS=== | ||
| + | |||
| + | Analysis drag dilakukan terlebih dahulu input data yang diperlukan pada ''CFD-Pre'' dan ''CFD-Solve''. Berikut adalah hasil setelah dilakukan ''Mesh Geometry'' dan ''Run Solver'' dari mobil yang akan dianalisa. | ||
| + | |||
| + | [[File:testcfdkel2_1.jpg|400px]] | ||
| + | |||
| + | Kemudian, pada bagian ''tab'' ''CFD-Post'', dilakukan running dengan aplikasi ''Paraview'' untuk mengetahui drag force yang ingin dicari tahu. | ||
| + | |||
| + | [[File:testcfdkel2_2.jpg|400px]] | ||
| + | |||
| + | Lalu, dilakukan pengerjaan dengan filter ''Generate Surface Normal'', dengan mengapply tampak car_body saja yang terlihat. Kemudian, dilakukan kalkulasi besar P terhadap gaya normal sumbu x. Hasil tersebut kemudian di apply kembali sehingga menghasilkan perhitungan yang diinginkan yaitu ''Drag Force'' yang ditentukan. Didapatkan besarnya setelah dilakukan ''filter'' dan integrasi perhitungan yang ada. Berikut adalah skema yang dilakukan: | ||
| + | |||
| + | [[File:testcfdkel2_3.jpg|400px]] | ||
| + | |||
| + | Kemudian, dilakukan percobaan lainnya dengan variasi V dengan interval 1 dari 10 hingga 20. Akhirnya, didapatkan data yang kemudian dibentuk grafiknya serta ''trendline'' yang berbentuk kurva sebagai berikut: | ||
| + | |||
| + | [[File:testcfdkel2_4.jpg|400px]] | ||
| + | |||
| + | |||
| + | ===Optimasi=== | ||
| + | Optimasi untuk kasus airfoil dilakukan menggunakan kode sbb: | ||
| + | |||
| + | # -*- coding: utf-8 -*- | ||
| + | """ | ||
| + | Created on Mon Dec 2 14:39:11 2019 | ||
| + | |||
| + | @author: rjsec | ||
| + | """ | ||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | |||
| + | def cdrag(x): | ||
| + | x1 = x[0] | ||
| + | drag = 0.0000003*x1**4-0.00002*x1**3+0.0008*x1**2+0.0026*x1-0.0517 | ||
| + | return drag | ||
| + | |||
| + | def clift(x): | ||
| + | x1 = x[0] | ||
| + | lift = 0.0000001*x1**4+0.00001*x1**3+0.0003*x1**2+0.0052*x1+0.0187 | ||
| + | return lift | ||
| + | |||
| + | def objective(x): | ||
| + | return cdrag(x) | ||
| + | |||
| + | def constraint1(x): | ||
| + | return 90 - cdrag(x) | ||
| + | def constraint2(x): | ||
| + | return 90 - clift(x) | ||
| + | |||
| + | con1=({'type':'ineq','fun':constraint1}) | ||
| + | con2=({'type':'ineq','fun':constraint2}) | ||
| + | cons = (con1,con2) | ||
| + | |||
| + | x1_guess = 50 | ||
| + | |||
| + | x0 = np.array([x1_guess]) | ||
| + | |||
| + | sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True}) | ||
| + | |||
| + | xopt = sol.x | ||
| + | forceopt = -sol.fun | ||
| + | |||
| + | dragopt = cdrag(xopt) | ||
| + | liftopt = clift(xopt) | ||
| + | |||
| + | print ("") | ||
| + | print ("Hasil optimasi:") | ||
| + | print ("Sudut optimal = "+str(-xopt[0])) | ||
| + | print ("Total force optimal = "+str(forceopt)) | ||
| + | print ("Drag force optimal = "+str(-dragopt)) | ||
| + | print ("Lift force optimal = "+str(liftopt)) | ||
| + | |||
| + | |||
| + | == Tugas Besar == | ||
| + | '''Spesifikasi Airfoil''' | ||
| + | [[File:TB1.png]] | ||
| + | Airfoil yang digunakan adalah MH 70 11.08% - Martin Hepperle MH70 | ||
| + | Span = 2 mm | ||
| + | Root and Tip Chord = 10 mm | ||
| + | |||
| + | '''Pembuatan model airfoil''' | ||
| + | Airfoil dibuat dengan menggunakan software Autodesk Inventor | ||
| + | [[File:TB2.png]] | ||
| + | |||
| + | '''Simulasi menggunakan CFD''' | ||
| + | Model yang sudah dibuat diimport ke CFDSOF | ||
| + | [[File:TB3.png]] | ||
| + | Model memasuki tahap ''meshing'' | ||
| + | |||
| + | Berikut adalah ''Boundary geometry'' untuk proses ''meshing'' | ||
| + | [[File:TB4.png]] | ||
| + | |||
| + | Model memasuki tahap-tahap analisis sebagai berikut | ||
| + | [[File:TB5.png]] | ||
| + | |||
| + | [[File:TB6.png]] | ||
| + | |||
| + | [[File:TB7.png]] | ||
| + | |||
| + | [[File:TB8.png]] | ||
| + | |||
| + | [[File:TB9.png]] | ||
| + | |||
| + | [[File:TB10.png]] | ||
| + | |||
| + | [[File:TB11.png]] | ||
| + | |||
| + | [[File:TB12.png]] | ||
| + | |||
| + | '''Perhitungan menggunakan Paraview''' | ||
| + | Model ''meshing'' diimport ke Paraview | ||
| + | Perhitungan dilakukan dengan tahap berikut | ||
| + | [[File:TB12.png]] | ||
| + | |||
| + | [[File:TB13.png]] | ||
| + | |||
| + | [[File:TB14.png]] | ||
| + | |||
| + | [[File:TB15.png]] | ||
| + | |||
| + | [[File:TB16.png]] | ||
| + | |||
| + | [[File:TB17.png]] | ||
| + | |||
| + | [[File:TB18.png]] | ||
| + | |||
| + | '''Hasil Percobaan''' | ||
| + | ''Data Percobaan'' | ||
| + | Data Percobaan | ||
| + | [[File:TB19.png]] | ||
| + | |||
| + | ''Grafik Percobaan'' | ||
| + | Berikut adalah grafik lift dan drag kami | ||
| + | [[File:TB20.png]] | ||
| + | |||
| + | ''Optimasi'' | ||
| + | Kode yang digunakan | ||
| + | [[File:TB21.png]] | ||
| + | |||
| + | Berikut hasil optimasi yang dilakukan | ||
| + | [[File:TB22.png]] | ||
| + | |||
| + | Grafik hasil optimasi Lift vs Drag | ||
| + | |||
| + | [[File:TB23.png]] | ||
| + | |||
Latest revision as of 18:41, 17 December 2019
Bismillahirrahmannirrahim ("Hello World!")
Jangan lupa istighfar dan berdoa sebelum melakukan sesuatu
Contents
Minggu 1
Mengapa kita harus belajar kalkulus?
Sebagai fondasi dasar untuk dapat mempelajari dan memahami mata kuliah lanjutan lainnya sekaligus melatih sense pelajar dalam menyelesaikan masalah yang berbasis logika
Phyton adalah salah satu bahasa pemrograman yang umum digunakan
Flowchart
Input --> Process --> Output
Pelajaran 1 minggu kedepan : pelajari Phyton, dan buat program untuk menyelesaikan suatu persoalan (dimulai dari alogaritmanya)
TUGAS 1
Python adalah salah satu dari banyaknya bahasa pemrograman. Python merupakan bahasa pemrograman yang paling sering digunakan di zaman modern ini.
Menyelesaikan persamaan (x^2-1)/(x-1) dengan menggunakan pyhthon.
def tugas(x):
result = (x**2-1)/(x-1)
try:
result
except ZeroDivisionError:
result = float('~')
return result
a = 1
b = a + 0.3
d = a - c
hasilnya = 0
jumlah = 0
while a < b+ 0.5:
d =d + 0.01
print(result(d))
a = a + 0.1
jumlah = jumlah + 1
if soal(d) != float('~'):
hasilnya = hasilnya + soal(d)
print("Limit = ")
print(hasilnya/jumlah)
Minggu 2
Kita harus mengenal terlebih dahulu partner kita dalam bekerja, yakni komputer
Pengertian bit
Praktik Langsung
Dasar-dasar programming + Phython
Diberi tugas dan mengerjakan dirumah
Mempelajari Tupple dan List
Tuple
Tuple adalah daftar yang berurutan dan terdiri dari beberapa elemen. Sebagai contoh tuple digunakan untuk menyimpan data seperti nama, nomor telepon, tempat dan tanggal lahir, email, dll.
List
List adalah kumpulan data yang berurutan maupun yang tidak berurutan. List dapat digunakan untuk menyimpan data kedalam daftar, mengurangi data, dan menambah data.
Minggu depan akan diadakan quiz 1 metnum
Minggu 3
Mempelajari penggunaan fungsi while, if, else, dan for
Mempraktikan penggunaan bahasa pemrograman untuk membuat deret bilangan Fibonacci
Penggunaan while
a=0
b=1
d=1
n1=input()
n=int(n1)
if(n==1):
c=1
else:
while(d<n):
c=a+b
a=b
b=c
d=d+1
print("Suku " + n1 + " adalah:")
print(c)
Penggunaan For
a=0
b=1
d=1
n1=input()
n=int(n1)
if(n==1):
c=1
else:
for d in range(n-1):
c=a+b
a=b
b=c
d=d+1
print("Suku " + n1 + " adalah:")
print(c)
Sebelum pekan depan sudah dibuatkan kelompok dan oekan depan sudah mengerjakan tugas kelompok
Minggu 4
Tugas Membuat program Gauss Elimination Saya dapat membuat program menghitung nilai X pada AX=B dengan metode Gauss Elimination. Namun masih memiliki kekurangan yaitu, hanya berlaku untuk matriks rectangular (nxn), dan Matrik B hanya memiliki 1 kolom.
a=[[2,-3,-1],
[3,2,-5],
[2,4,-4]]
b =[[3],
[-9],
[-5]]
c=[1,1,1,1,1,1,1,1]
n=len(b)
#Elimination
for k in range(0,n-1):
for i in range(n-1,k,-1):
if a[i][k] != 0.0:
op= a[i][k]/a[i-1][k]
b[i][0]=b[i][0]-op*b[i-1][0]
for f in range(0,n):
a[i][f]=a[i][f]-op*a[i-1][f]
#Subtitution
if a[n-1][n-1] != 0:
c[n-1]=b[n-1][0]/a[n-1][n-1]
else:
c[n-1]=0
for i in range(n-2,-1,-1):
sigma=0
for k in range(0,n,1):
y=a[i][k]*c[k]
sigma=sigma+y
sigma=sigma-a[i][i]
if a[i][i] != 0:
c[i]=(b[i][0]-sigma)/a[i][i]
else:
a[i][i] =0
for v in range(0,n,1):
print(a[v])
print(c[0:n])
Perhatikan dosen dan serap ilmunya, jangan bukunya
Mechanical modelling seperti stress
Parameter elastisitas (keengganan untuk berubah bentuk) sebagai sifat bahan
kita makhluk yang sangat dimuliakan
kenalkan pancasila,
modeling kasus engineering dengan metnum
parameter secara pyshically
Macam macam tegangan
Mengurangi kebenaran, karena pengurangan asumsi pada simulasi
Keadaan disederhanakan terus
Tugas saya menyusun persamaan diatas untuk tiap titik
Minggu 5
Phyton adalah bahasa pemrograman yang umum digunakan Modelling spring system Modelling menggunakan matrix system Penggunaan Third Party Tool seperti Numpy dan Simpy
Minggu 6
Peran komputer adalah sebagai tool dalam menyelesaikan modelling Asumsi kontinuum, homogen, dan konstan Imagination is more powerful than knowledge Kontinuum adalah sebuah notasi dimana ketika variabel terikat memiliki perubahan yang sangat kecil mendekati 0 akan memiliki nilai yang sama Percaya akan tuhan, surga, dan neraka Metode numerik merupakan Computer Aided Engineering Penjelasan runge kutta untuk penyelesaian persamaan turunan.
Minggu 7
Diadakan kuis
UTS
Muhasabah UTS
Problem A
#Menentukan nilai gravitasi
g=float(input("Masukkan nilai g(m/s^2):"))
#Menentukan nilai m4
m4=float(input("Masukkan nilai m4(kg):"))
#Menentukan nilai m3
m3=float(input("Masukkan nilai m3(kg):"))
#Menentukan nilai m2
m2=float(input("Masukkan nilai m2(kg):"))
#Menentukan nilai m1
m1=float(input("Masukkan nilai m1(kg):"))
#Pengoperasian mencari nilai sin a
sina=m4/(m3+m2+m1)
#Menghitung nilai T3
T3=m4*g
#Menghitung nilai T2
T2=T3-(m3*g*sina)
#Menghitung nilai T1
T1=m1*g*sina
#print nilai T3
print("Besar T3:",T3,"N")
#print nilai T2
print("Besar T2:",T2,"N")
#print nilai T1
print("Besar T1:",T1,"N")
Problem B
#Menentukan nilai gravitasi
g=float(input("Masukkan nilai g(m/s^2):"))
#Menentukan nilai massa mobil
m=float(input("Masukkan nilai massa mobil(kg):"))
#Menentukan nilai koefisien gesek
cs=float(input("Masukkan nilai cs:"))
#Menentukan nilai koefisien drag udara
cd=float(input("Masukkan nilai cd:"))
#Menentukan nilai a
a=float(input("Masukkan nilai a(m/s^2):"))
#Menentukan nilai xo
xo=float(input("Masukkan nilai xo(m):"))
#Menentukan nilai vo
vo=float(input("Masukkan nilai vo(m/s):"))
#Menentukan nilai vmaks
vmaks=float(input("Masukkan nilai vmaks(m/s):"))
#Pengoperasian mencari nilai gaya gesek
frik=m*g*cs
din=cd*vmaks**2
#Pengoperasian mencari tmaks
tmaks=(vmaks-xo)/(a-(m*g*cs)-(cd*vmaks**2))
#Menghitung nilai xmaks
xmaks=xo+vo*tmaks+(0.5*a*tmaks**2)-(0.5*frik*tmaks**2)-(0.5*din*tmaks**2)
#print nilai tmaks
print("t saat vmaks:",tmaks,"s")
#print nilai T3
print("x saat vmaks",xmaks,"m")
test
m = eval(input("massa mobil : "))
g = 9.81
cd = eval(input("koefisien drag udara : "))
frik = eval(input("koefisien gesek jalan : "))
hp = eval(input("Besar Horsepower mobil : "))
rpm = eval(input("Besar RPM mobil : "))
sina = eval(input("Besar sina bidang miring: "))
cosa = eval(input("Besar cosa bidang miring: "))
v = 0
t = 0
dt = 1 #tinggi step atau waktu
error = 100
Fmobil = (hp * 9550) / (rpm * ((2 * 3.14)/60))
p = (Fmobil/m) - g*frik
q = cd/m
def dvdt(t, v):
return p-(q*(v)**(1.5))-(cosa*frik*g)-(sina*g)
while error > 0.005:
k1 = dvdt(t, v)
k2 = dvdt(t + 0.5 * h, v + 0.5 * h * k1)
k3 = dvdt(t + 0.5 * h, v + 0.5 * h * k2)
k4 = dvdt(t + h, v + h * k3)
v1 = v + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
t = t + h
error = ((v1 - v) / v1)*100 #persentase error
v = v1
lst.append(v1)
waktu = len(lst)
print ("waktu untuk mencapai velocity maksimal adalah: ", waktu+1)
print ("velocity maksimal adalah: ", v1)
Minggu 10
Kasus fisika nyata runge-kutta
Minggu 11
Penjelasan mengenai gelombang Sarjana dituntut merumuskan masalah kemudian menemukan solusi Sales mobil menjual mobil dengan spesifikasi power dan torque
Minggu 12
Terdapat banyak cara pengelolaan data Terdapat error dalam suatu pengelolaan data Dilakukan optimasi sebagai pengurangan error Optimasi dilakukan untuk mencari nilai efektif
Minggu 13
Penggunaan CFDSOF Penggunaan Paraview Menghitung gaya drag dan gaya lift
Minggu 14
Quiz Soal yang diberikan berupa soal yang sudah diberikan sebelumnya Sebagai review Presentasi kelompok yang sudah selesai
===CFD CAR DRAG ANALYSIS===
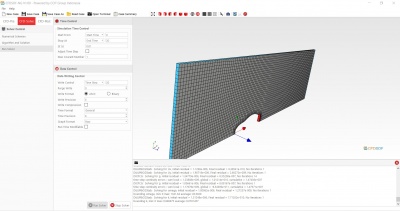
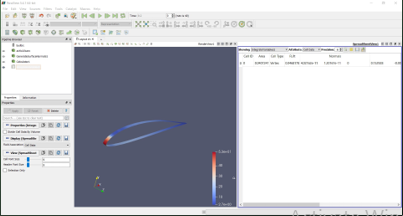
Analysis drag dilakukan terlebih dahulu input data yang diperlukan pada CFD-Pre dan CFD-Solve. Berikut adalah hasil setelah dilakukan Mesh Geometry dan Run Solver dari mobil yang akan dianalisa.
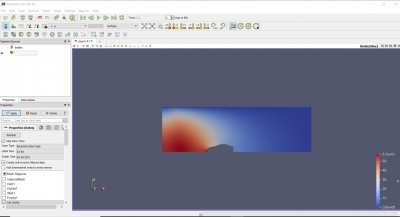
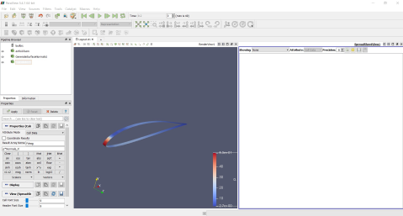
Kemudian, pada bagian tab CFD-Post, dilakukan running dengan aplikasi Paraview untuk mengetahui drag force yang ingin dicari tahu.
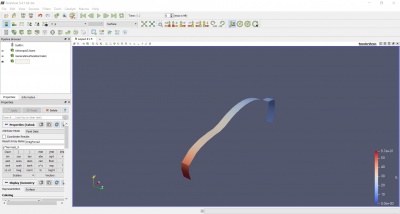
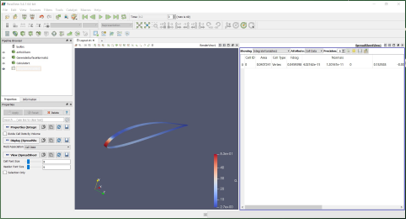
Lalu, dilakukan pengerjaan dengan filter Generate Surface Normal, dengan mengapply tampak car_body saja yang terlihat. Kemudian, dilakukan kalkulasi besar P terhadap gaya normal sumbu x. Hasil tersebut kemudian di apply kembali sehingga menghasilkan perhitungan yang diinginkan yaitu Drag Force yang ditentukan. Didapatkan besarnya setelah dilakukan filter dan integrasi perhitungan yang ada. Berikut adalah skema yang dilakukan:
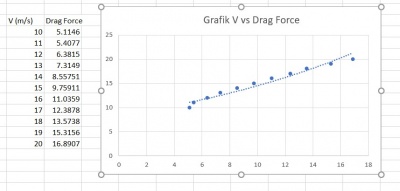
Kemudian, dilakukan percobaan lainnya dengan variasi V dengan interval 1 dari 10 hingga 20. Akhirnya, didapatkan data yang kemudian dibentuk grafiknya serta trendline yang berbentuk kurva sebagai berikut:
Optimasi
Optimasi untuk kasus airfoil dilakukan menggunakan kode sbb:
# -*- coding: utf-8 -*-
"""
Created on Mon Dec 2 14:39:11 2019
@author: rjsec
"""
import numpy as np
from scipy.optimize import minimize
def cdrag(x):
x1 = x[0]
drag = 0.0000003*x1**4-0.00002*x1**3+0.0008*x1**2+0.0026*x1-0.0517
return drag
def clift(x):
x1 = x[0]
lift = 0.0000001*x1**4+0.00001*x1**3+0.0003*x1**2+0.0052*x1+0.0187
return lift
def objective(x):
return cdrag(x)
def constraint1(x):
return 90 - cdrag(x)
def constraint2(x):
return 90 - clift(x)
con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
xopt = sol.x
forceopt = -sol.fun
dragopt = cdrag(xopt)
liftopt = clift(xopt)
print ("")
print ("Hasil optimasi:")
print ("Sudut optimal = "+str(-xopt[0]))
print ("Total force optimal = "+str(forceopt))
print ("Drag force optimal = "+str(-dragopt))
print ("Lift force optimal = "+str(liftopt))
Tugas Besar
Spesifikasi AirfoilAirfoil yang digunakan adalah MH 70 11.08% - Martin Hepperle MH70 Span = 2 mm Root and Tip Chord = 10 mm
Pembuatan model airfoil Airfoil dibuat dengan menggunakan software Autodesk Inventor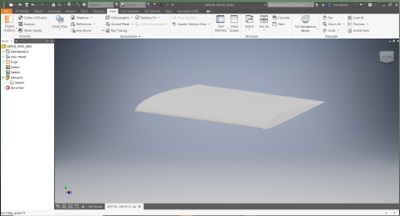
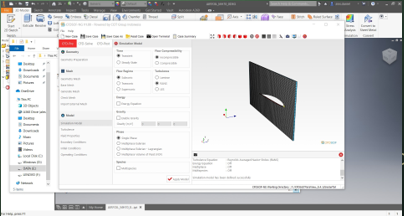
Simulasi menggunakan CFD Model yang sudah dibuat diimport ke CFDSOFModel memasuki tahap meshing Berikut adalah Boundary geometry untuk proses meshing
Model memasuki tahap-tahap analisis sebagai berikut
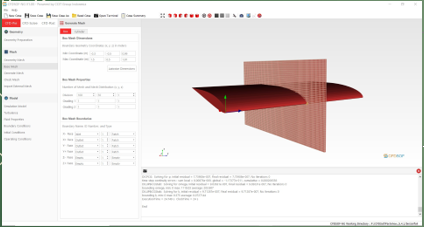
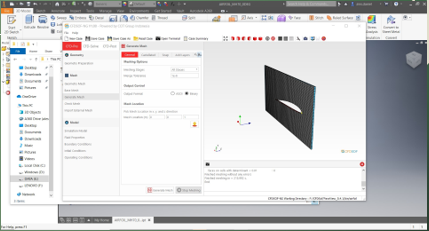
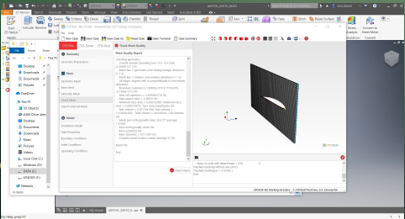
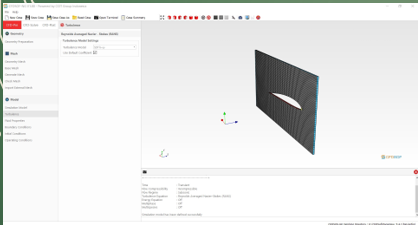
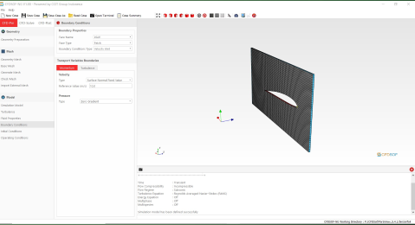
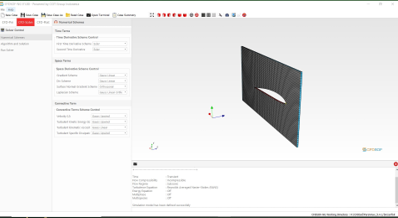
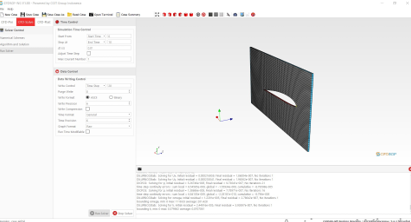
Perhitungan menggunakan Paraview Model meshing diimport ke Paraview Perhitungan dilakukan dengan tahap berikut
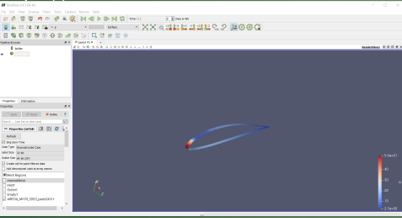
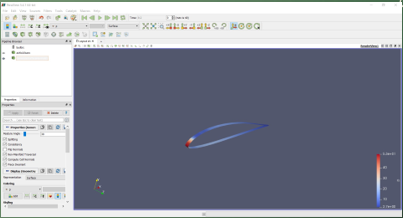
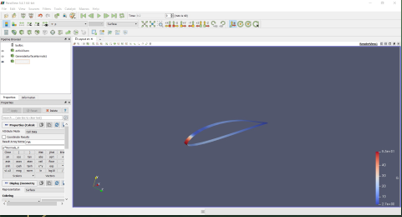
Hasil Percobaan Data Percobaan Data PercobaanGrafik Percobaan Berikut adalah grafik lift dan drag kami
Optimasi Kode yang digunakan
Berikut hasil optimasi yang dilakukan
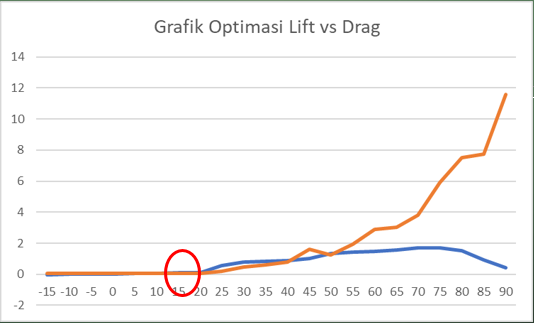
Grafik hasil optimasi Lift vs Drag
Minggu 15
Presentasi CFDSOF
Minggu 16
Mempelajari tentang ANN (Artificial Neural Network) Terinspirasi dari otak manusia Digunakan dalam klasifikasi dan prediksi Tahapan-tahapan membuat ANN