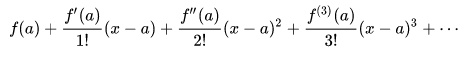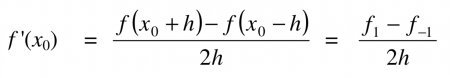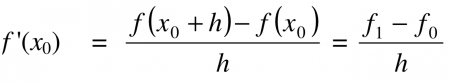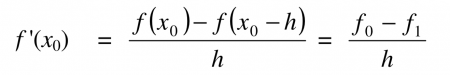Difference between revisions of "Nur Akhmad Fajar"
(→Tugas 1 (Selasa, 29 Oktober 2019)) |
(→Runge Kutta Method (Selasa, 5 November 2019)) |
||
| Line 136: | Line 136: | ||
== '''Runge Kutta Method''' (Selasa, 5 November 2019) == | == '''Runge Kutta Method''' (Selasa, 5 November 2019) == | ||
| + | |||
| + | Pada kelas ini kami diberitahu bahwa penyelesaian Metode Numerik dapat diselesaikan dengan metode Brainware, Software, dan Hardware. Dalam menyelesaikan masalah sehari-hari atau kita dapat menyebutnya Engineering Problem (Real Life Case) kita dapat menggunakan metode yang telah disebutkan diatas. Untuk menyelesaikannya kita harus menentukan Initial Value Problem dan Boundary Value Problem dimana pada kasus yang telah diberikan dikelas yaitu, top speed dan aerodynamics. Dengan membuat model yang berupa physical atau math kita dapat menyelesaikan permasalahan engineering yang ada. Lalu setelah model tersebut ada, kita harus dapat menganalisis permasalahan dan modelnya agar dapat ditemukan solusi yang valid dari model tersebut yang disebut dengan Analysis Result. Agar lebih memudahkan pekerjaan kita, dapat digunakan software yang telah ada untuk memecahkan masalahnya. Beberapa software yang dapat digunakan adalah CFD, FEA, AI (Neural Network) dan Optimization. | ||
| + | |||
| + | '''Runge Kutta Method''' | ||
| + | |||
| + | Ini adalah merupakan metode alternatif selain Deret Taylor, dalam penggunaannya kita menggunakan metode turunan seperti dibawah ini | ||
| + | |||
| + | [[File:Runge.png]] | ||
Revision as of 17:31, 16 December 2019
Contents
- 1 Profil
- 2 Deret Taylor (Selasa, 3 September 2019)
- 3 Tingkatan Bahasa Komputer, merangkai pseudocode (Selasa, 10 September 2019)
- 4 Turunan Numerik (Selasa, 17 September 2019)
- 5 Root Finding Algoritma (Selasa, 24 September 2019)
- 6 Tugas 1 (Selasa, 29 Oktober 2019)
- 7 Runge Kutta Method (Selasa, 5 November 2019)
Profil
Nama : Nur Akhmad Fajar
NPM : 1606824774
Jurusan : Teknik Mesin
Deret Taylor (Selasa, 3 September 2019)
Metode Numerik
1. Summary
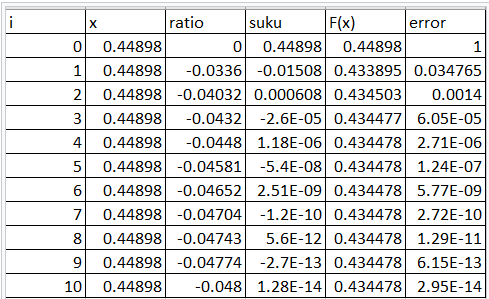
Pada hari Selasa, 3 September 2019 kami pertama kali diajarkan cara untuk memecahkan masalah dari perhitungan matematika yang sulit. Cara tersebut dinamakan Metode Numerik. Pada hari tersebut kami diajarkan oleh Dr. Ir. Engkos Achmad Kosasih M.T. dan Dr. Ir. Ahmad Indra Siswantara. Metode numerik merupakan salah satu cara untuk mengaproksimasi sebuah fungsi yang terkadang sulit untuk dicari nilai dari akar-akarnya dengan perhitungan sederhana. Pada kelas Metode Numerik hari Selasa, 3 September 2019 kami diperkenalkan dengan Deret Taylor atau Deret Maclaurin. Kami diminta menggunakan program Microsoft Excel untuk mencari nilai sinus dari f(pi/7). Hal ini dapat dipecahkan dengan menggunakan rumus Deret Taylor seperti di bawah ini
2. Lalu untuk pengaplikasiannya dalam excel berikut saya lampirkan
Tingkatan Bahasa Komputer, merangkai pseudocode (Selasa, 10 September 2019)
Untuk bahasa komputer yang paling rendah dinamakan binary atau bahasa permesinan. Binary tersebut menggunakan angka 1 dan 0 untuk pengoperasiannya. Angkan 1 dan 0 tersebut akan dikombinasikan sehingga dapat membuat suatu perintah. Perintah yang harus diaplikasikan sangatlah banyak, namun kita hanya dapat menggunakan kombinasi antara 1 dan 0 untuk memberi perintah tersebut. Hal ini membuat bahasa tersebut sangat sulit dipahami untuk para pemula. Maka dari itu, dibuatlah bahasa penerjemah yang mana bahasa tersebut akan diterjemahkan kembali ke bahasa binary dengan menggunakan komputer. Penerjemah ini disebut sebagai compiler.
Compiler ini menggunakan aplikasi-aplikasi khusus pada komputer. Berbeda dengan aplikasi yang ada pada komputer, pseudocode adalah bahasa ada pemrograman yang tidak dapat diterjemahkan ke bahasa mesin (binary) karena tidak ada aplikasi yang dapat menerjemahkannya. Berikut adalah contoh pseudocode yang telah dibuat di kelas :
I = r ; err = 1
suku = x
sin = suku
while err > 1e-7
{
ratio = -x^2/((2*I)*(2*I+1))
suku = suku*ratio
err = abs(suku/sin)
sin = sin + suku
I = I+1
}
Turunan Numerik (Selasa, 17 September 2019)
Dalam turunan numerik kita harus menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 jenis turunan numerik, yaitu maju, mundur, dan center. Dalam perhitungannya harus digunakan alat seperti komputer atau kalkulator agar lebih memudahkan kita. Untuk nilai h yang sama, maka jenis center dapat digunakan pada turunan numerik tersebut, namum untuk maju dan mundur dapat digunakan apabila terdapat tingkat keakuratan yang sama. pada kelas ini kita mengidentifikasi metode yang akan digunakan berdasarkan data yang ada. Berikut adalah metodenya :
1. Turunan Center
2. Turunan Maju
3. Turunan Mundur
Root Finding Algoritma (Selasa, 24 September 2019)
Pada kesempatan kali ini diberikan materi yaitu Root Finding Algoritma. Materi tersebut adalah algoritma yang digunakan untuk mencari nilai nol atau roots dari fungsi sebuah persamaan. Dapat digunakan 3 metode dalam Root Finding Algoritma, yaitu:
1. Newton-Raphson Method
Newton-Raphson Method adalah metode dengan pendekatan satu titik untuk mencari akar dari suatu fungsi f(x), dimana fungsi f(x) memiliki turunan
2. Bisect Method
Bisect method adalah metode yang dengan membagi dua bagian, dari dua bagian tersebut lalu ditentukan yang terdapat akar dan tidak terdapat akar.
3. Secant Method
Secant method adalah metode yang menggunakan garis secant untuk mengaproksimasi nilai sebuah fungsi (gradien garis yang melalui titik (x_0),ff(x_0)) dan (x_1, f(x_1)))
Tugas 1 (Selasa, 29 Oktober 2019)
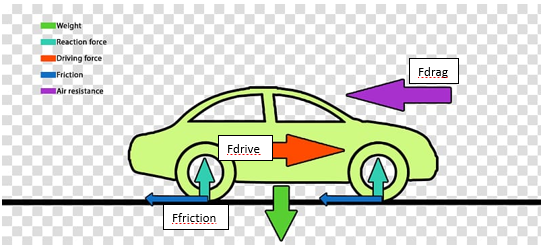
Pada kesempatan kali ini saya akan menjawab persoalan yang diberikan pada kelas mata kuliah metode numerik. Persoalan yang diberikan adalah mahasiswa harus membuat pseudocode dari governing equation sebuah mobil untuk mencari waktu yang ditempuh mobil untuk mencapai kecepatan maksimal
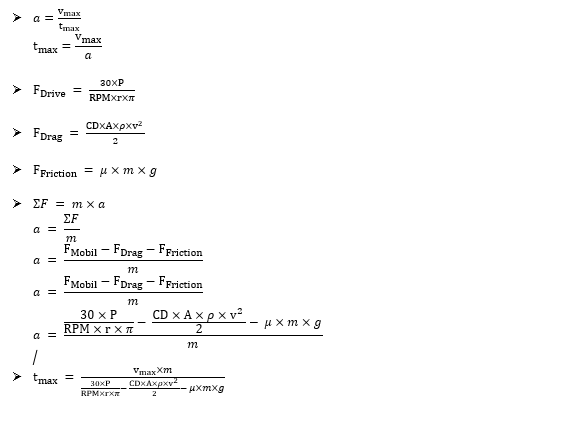
Pseudocode dari Governing Equation diatas yaitu
import math
g = 9.81
phi = 3.14
rho = 1.2
P = eval (input('Daya Mesin Mobil: '))
RPM = eval (input('Putaran Mesin mobil: '))
r = eval (input('Jari-jari Ban mobil: '))
CD = eval (input('Koefisien Hambat Udara: '))
A = eval (input('Luas Permukaan Mobil: '))
vmax = eval (input('Kecepatan maksimum mobil: '))
CF = eval (input('Koefisien Gesek: '))
m = eval (input('massa mobil: '))
Fmobil = (30*P)/(RPM*r*phi)
Fdrag = (CD*A*rho*vmax^2)/2
Ffriction = CF*m*g
tmax = (vmax*m)/(Fmobil-Fdrag-Ffriction)
print ('waktu yang dibutuhkan mobil untuk mencapai kecepatan maksimumnya: ',tmax)
Runge Kutta Method (Selasa, 5 November 2019)
Pada kelas ini kami diberitahu bahwa penyelesaian Metode Numerik dapat diselesaikan dengan metode Brainware, Software, dan Hardware. Dalam menyelesaikan masalah sehari-hari atau kita dapat menyebutnya Engineering Problem (Real Life Case) kita dapat menggunakan metode yang telah disebutkan diatas. Untuk menyelesaikannya kita harus menentukan Initial Value Problem dan Boundary Value Problem dimana pada kasus yang telah diberikan dikelas yaitu, top speed dan aerodynamics. Dengan membuat model yang berupa physical atau math kita dapat menyelesaikan permasalahan engineering yang ada. Lalu setelah model tersebut ada, kita harus dapat menganalisis permasalahan dan modelnya agar dapat ditemukan solusi yang valid dari model tersebut yang disebut dengan Analysis Result. Agar lebih memudahkan pekerjaan kita, dapat digunakan software yang telah ada untuk memecahkan masalahnya. Beberapa software yang dapat digunakan adalah CFD, FEA, AI (Neural Network) dan Optimization.
Runge Kutta Method
Ini adalah merupakan metode alternatif selain Deret Taylor, dalam penggunaannya kita menggunakan metode turunan seperti dibawah ini