Difference between revisions of "Kelompok 3"
Wildan.zulfa (talk | contribs) (→Tugas Simulasi CFD Pada Mobil) |
Wildan.zulfa (talk | contribs) (→Tugas Optimasi CFD Airfoil) |
||
| Line 124: | Line 124: | ||
== '''Tugas Optimasi CFD Airfoil''' == | == '''Tugas Optimasi CFD Airfoil''' == | ||
| + | |||
| + | |||
| + | Silahkan berkomentar pada kolom di bawah | ||
| + | |||
| + | <comments voting="Plus" /> | ||
Revision as of 12:31, 15 December 2019
Perkenalkan, Kami dari kelompok 3 dengan anggota
1. Candra Steven
2. Fahmi Ismail Wibisono
3. Wildan Zulfa Abdurrohman
Contents
Metode Eliminasi Gauss
Eliminisasi Gauss adalah metode untuk mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana. Dengan melakukan operasi baris sehingga matriks tersebut menjadi salah satu metode penyelesaian persamaan linear.
Contoh soal
Pengerjaan Matematis
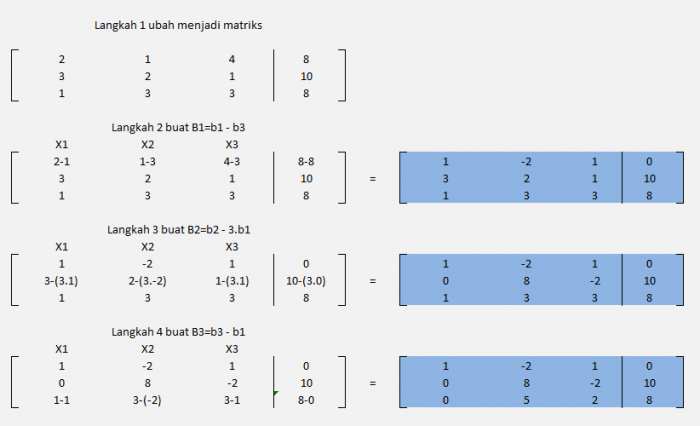
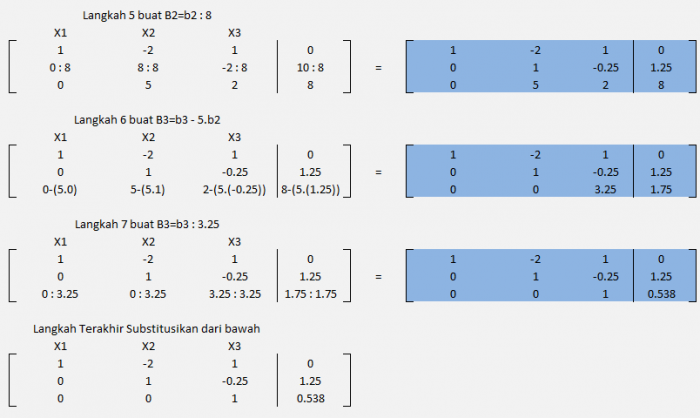
Menggunakan Eliminasi Gauss
Kemudian menyelesaikan dengan Subtitusi
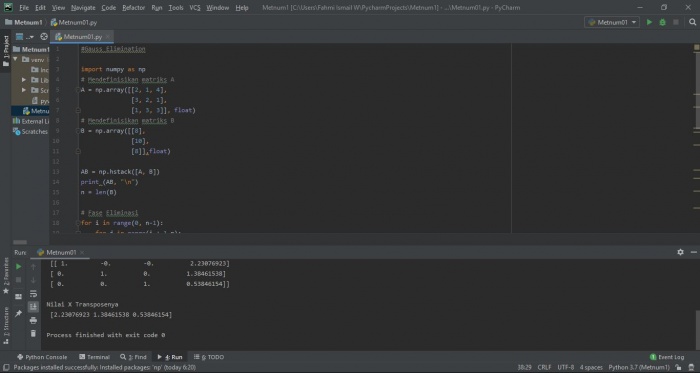
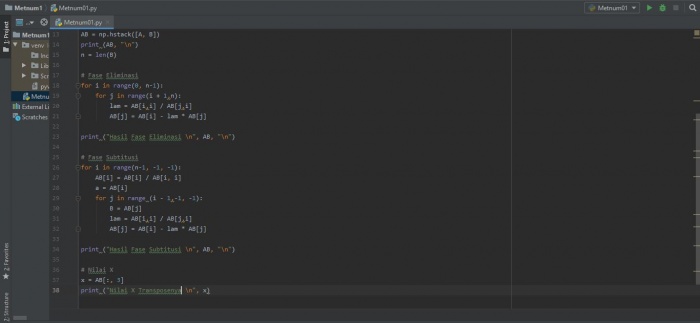
Pengerjaan Menggunakan Bahasa Python
Dalam penggunaan matriks pada bahasa python dibutuhkan fungsi array dengan cara import numpy
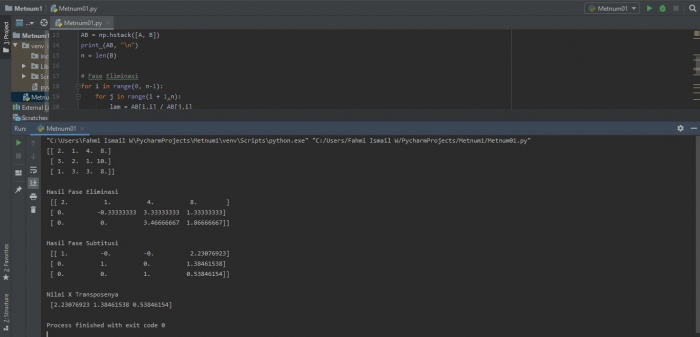
Hasil perhitungan dengan Python
Program Python
Runge Kutta
Pada tanggal 9 Oktober 2019, kami diberikan tugas untuk membuat persamaan pegas dengan metode Runge Kutta. Soalnya adalah sebagai berikut
Penyelesaian dari soal ini dapat diselesaikan dengan coding sebagai berikut
# Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01.
x0 = 0
y = 0
h = 0.01
x = float(input("Masukkan nilai t: "))
if 0 <= x < 2:
# dydx menyatakan persamaan awal dalam soal. Persamaan harus diintegralkan sekali untuk menghasilkan persamaan kecepatan.
# Didapat hasil 2x^2 - 30xy karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
# P(t) dinyatakan dalam x.
def dydx(x, y):
return (2*x**2 - 30*x*y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x selanjutnya
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 2:
# Ketika x >= 2, perhitungan harus diganti karena P(t) sudah konstan di angka 20 N.
def dydx(x, y):
return (8 - 30*x*y)
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
else:
print("Mohon masukkan nilai t positif.")
Tugas Simulasi CFD Pada Mobil
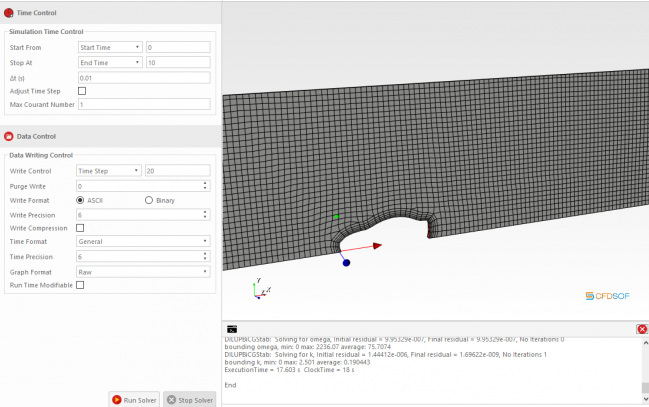
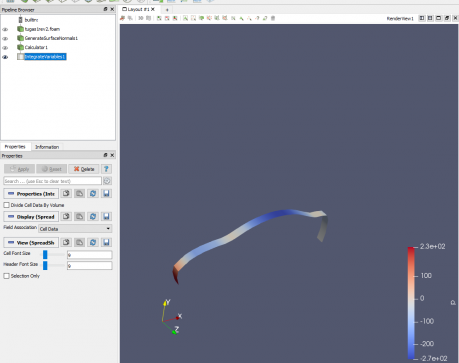
Tugas Optimasi CFD Airfoil
Silahkan berkomentar pada kolom di bawah
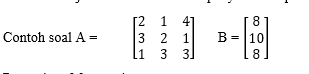




Enable comment auto-refresher