Difference between revisions of "Rivaldo Marta"
Rivaldomarta (talk | contribs) |
Rivaldomarta (talk | contribs) |
||
| Line 110: | Line 110: | ||
Soal B | Soal B | ||
---- | ---- | ||
| + | def TurunanV(t, v): #Fungsi Turunan V terhadap t | ||
| + | return ((a - cd*vt**3/2)/m) | ||
| + | |||
#memasukkan nilai variabel yang diperlukan | #memasukkan nilai variabel yang diperlukan | ||
cd=eval(input("drag coefficient: ")) | cd=eval(input("drag coefficient: ")) | ||
| − | v0=eval(input("initial velocity (m/s): ")) | + | v0=eval(input("initial velocity(m/s): ")) |
m=eval(input("mass (kg): ")) | m=eval(input("mass (kg): ")) | ||
a=eval(input("acceleration (m/s^2): ")) | a=eval(input("acceleration (m/s^2): ")) | ||
vt=eval(input("top speed (m/s): ")) | vt=eval(input("top speed (m/s): ")) | ||
| − | # | + | xinitial = 0 #x awal |
| − | + | yinitial = 0 #y awal | |
| − | + | x = vt | |
| − | + | h = 0.2 #delta yang digunakan | |
| − | + | ||
| − | print("waktu | + | |
| + | nilai = (int)((x - xinitial)/h) #menghitung jumlah increment | ||
| + | for i in range(1, nilai + 1): | ||
| + | k1 = h * TurunanV(xinitial, yinitial) #runge kutta | ||
| + | k2 = h * TurunanV(xinitial + 0.5 * h, yinitial + 0.5 * k1) | ||
| + | k3 = h * TurunanV(xinitial + 0.5 * h, yinitial + 0.5 * k2) | ||
| + | k4 = h * TurunanV(xinitial + h, yinitial + k3) | ||
| + | |||
| + | yinitial = yinitial + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | xinitial = xinitial + h #menambahkan xawal besarkan delta h | ||
| + | print("maka waktu yang dibutuhkan adalah",yinitial, "detik") | ||
[[File:Rivaldo Marta Problem 2.mp4]] | [[File:Rivaldo Marta Problem 2.mp4]] | ||
Revision as of 00:53, 6 November 2019
Nama: Rivaldo Marta
NPM : 1706036324
بِسْمِ اللَّهِ الرَّحْمَنِ الرَّحِيمِ
Contents
Pengenalan Metode Numerik
Mengapa Anak Mesin Perlu Belajar Kalkulus?
Sebagai Mahasiswa Mesin yang nantinya akan menjadi sarjana teknik, perlu untuk memiliki analisis yang tepat dalam menyelesaikan permasalahan yang dihadapi nanti. Sarjana teknik harus mampu memodelkan dan mensimulasikan permasalahan yang ada sehingga dapat ditentukan perhitungan yang tepat untuk mendapatkan pemecahan masalah yang tepat. Perhitungan yang tepat dapat dicapai dengan memahami konsep Kalkulus yang tepat.
Pengertian Metode Numerik
Menurut ahli matematika seperti Chapra dan Chanale (1991) berpendapat bahwa pengertian metode numerik adalah teknik penyelesaian masalah secara matematis dg operasi aritmetika melalui formulasi tertentu. Secara umum,metode numerik adalah tool matematis yang dirancang untuk menyelesaikan masalah numerik (angka atau bilangan). Implementasi dari numerical method yang dilengkapi dengan kaidah pemeriksaan konvergensi yang sesuai dalam bahasa pemrograman disebut dengan algoritma numerik (numerical algorithm).
Dalam pembelajaran ini, Bahasa pemrograman yang digunakan adalah Python. Bahasa pemrograman berguna untuk mengubah perintah user menjadi Bahasa yang dapat dijalankan oleh software yang digunakan untuk memecahkan permasalahan yang ada. Bahasa pemrograman dapat dijelaskan melalui flowchart, yaitu bagan-bagan yang berisi tahapan selama proses coding.
Menyelesaikan Persoalan Matematis
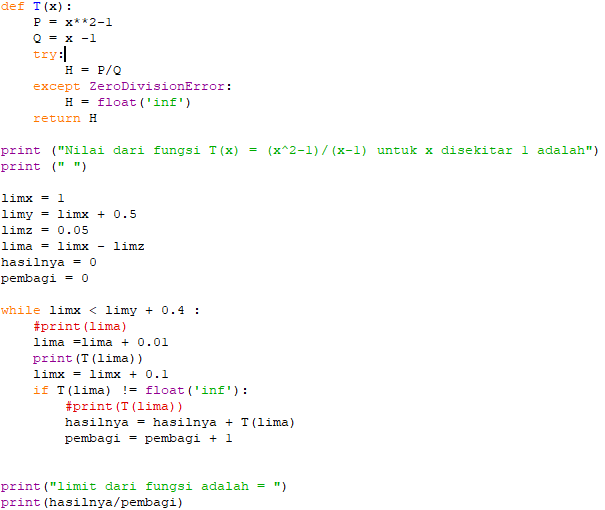
Misalkan mencari limit x mendekati 1 untuk fungsi T(x) = (x^2-1)/(x-1)
setelah Python di run, akan muncul hasil sebagai berikut
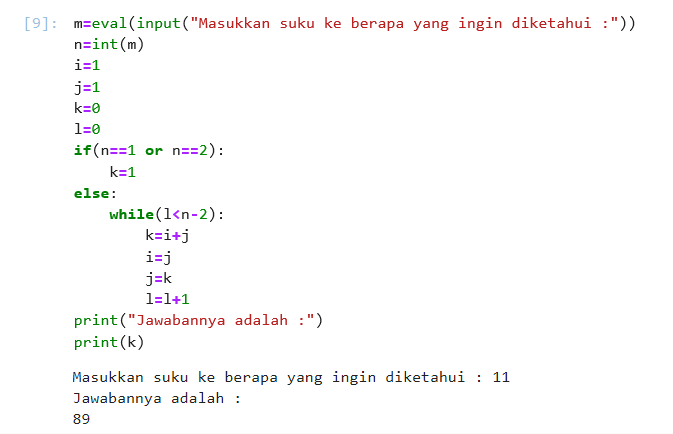
Deret Fibonacci
Deret Fibonacci adalah sebuah pola bilangan yang diperoleh dari penjumlahan dua bilangan sebelumnya di dalam deret tersebut.
Quiz 16 Oktober 2019
Soal Problem set 2.1 no 6
from numpy import linalg import numpy as np
#memasukkan nilai-nilai matriks
A= np.array ([[0,0,2,1,2] ,[0,1,0,2,-1], [1,2,0,-2,1], [0,0,0,-1,1], [0,1,-1,1,-1]])
B= np.array ([[1], [1], [-4], [-2], [-1]])
H= np.array ([[0,0,2,1,2,1] ,[0,1,0,2,-1,1], [1,2,0,-2,1,-4], [0,0,0,-1,1,-2], [0,1,-1,1,-1,-1]]) #matriks untuk dilakukan operasi gauss elimination
print ('Matrix A :')
print (A)
print ('Matrix B :')
print (B)
print ('persamaan Gaus-Elimination :')
print (H)
#akan dicari nilai matrix X menggunakan library linalg
matrix = A
sols = B
persamaan = linalg.solve (matrix,sols)
x1 = int(row1[0])
x2 = int(row2[1])
x3 = int(row3[2])
x4 = int(row4[3])
x5 = int(row5[4])
hasil= (x1, x2, x3, x4, x5)
print ("maka matrix X adalah :")
print (hasil)
Hasil Coding dan Video Penjelasan UTS
Soal A
from math import*
#memasukkan variabel yang dipelukan
g=9.81
m1=eval(input("massa 1 dalam kg: "))
m2=eval(input("massa 2 dalam kg: "))
m3=eval(input("massa 3 dalam kg: "))
alpha=eval(input("sudut dalam radian: "))
ms=eval(input("koefisien gesek statis: "))
y=sin(alpha)
x=cos(alpha)
z=(y-ms*x)
T1=m1*g*z
T2=T1+m2*g*z
T3=T2+m3*g*z
m4=T3/g
print("nilai T1 adalah: ", T1, "Newton")
print("nilai T2 adalah: ", T2, "Newton")
print("nilai T3 adalah: ", T3, "Newton")
print("nilai m4 adalah: ", m4, "kilogram")
Soal B
def TurunanV(t, v): #Fungsi Turunan V terhadap t
return ((a - cd*vt**3/2)/m)
#memasukkan nilai variabel yang diperlukan
cd=eval(input("drag coefficient: "))
v0=eval(input("initial velocity(m/s): "))
m=eval(input("mass (kg): "))
a=eval(input("acceleration (m/s^2): "))
vt=eval(input("top speed (m/s): "))
xinitial = 0 #x awal
yinitial = 0 #y awal
x = vt
h = 0.2 #delta yang digunakan
nilai = (int)((x - xinitial)/h) #menghitung jumlah increment
for i in range(1, nilai + 1):
k1 = h * TurunanV(xinitial, yinitial) #runge kutta
k2 = h * TurunanV(xinitial + 0.5 * h, yinitial + 0.5 * k1)
k3 = h * TurunanV(xinitial + 0.5 * h, yinitial + 0.5 * k2)
k4 = h * TurunanV(xinitial + h, yinitial + k3)
yinitial = yinitial + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
xinitial = xinitial + h #menambahkan xawal besarkan delta h
print("maka waktu yang dibutuhkan adalah",yinitial, "detik")
Video Muhasabah
Berikut adalah video muhasabah dan evaluasi diri saya selama pembelajaran setengah semester Metode Numerik
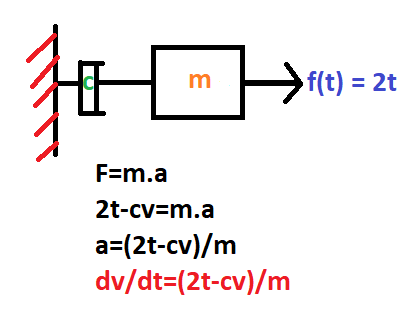
Permodelan Sistem Getaran Mekanik
dV/dt=(f(t)-cv)
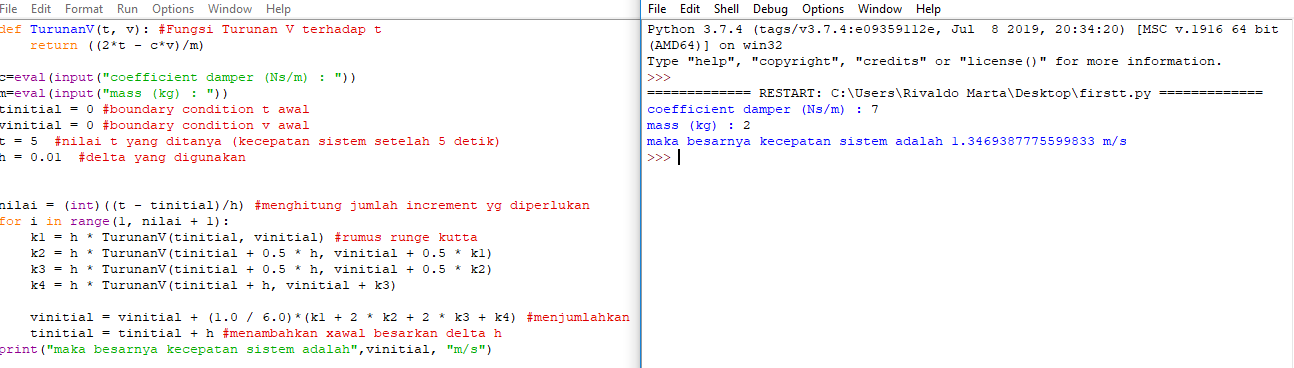
Coding Sistem
def TurunanV(t, v): #Fungsi Turunan V terhadap t
return ((2*t - c*v)/m)
c=eval(input("coefficient damper (Ns/m) : "))
m=eval(input("mass (kg) : "))
tinitial = 0 #t awal
vinitial = 0 #v awal
t = 5 #nilai t yang ditanya (kecepatan sistem setelah 5 detik)
h = 0.01 #delta yang digunakan
nilai = (int)((t - tinitial)/h) #menghitung jumlah increment
for i in range(1, nilai + 1):
k1 = h * TurunanV(tinitial, vinitial) #runge kutta
k2 = h * TurunanV(tinitial + 0.5 * h, vinitial + 0.5 * k1)
k3 = h * TurunanV(tinitial + 0.5 * h, vinitial + 0.5 * k2)
k4 = h * TurunanV(tinitial + h, vinitial + k3)
vinitial = vinitial + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #menjumlahkan nilai k1,k2,k3,k4 ke y' yang baru dan membaginya
tinitial = tinitial + h #menambahkan xawal besarkan delta h
print("maka besarnya kecepatan sistem adalah",vinitial, "m/s")


Enable comment auto-refresher