Difference between revisions of "Pemodelan Fisika kasus nyata-Runge kutta"
(Created page with "__TOC__ == Study-case == Studi kasus yaitu roket yang diterbangkan lalu jatuh bebas diudara menuju permukaan bumi. == Algoritma == Kasus ini dapat diselesaikan dengan met...") |
|||
| Line 70: | Line 70: | ||
return v | return v | ||
print("Kecepatan roket setelah", t, "detik jatuh adalah", rungekutta(t0, v0, t, step), "m/s") | print("Kecepatan roket setelah", t, "detik jatuh adalah", rungekutta(t0, v0, t, step), "m/s") | ||
| − | [[File: | + | |
| − | [[File:prbaru2.png| | + | [[File:prbaru_1.png|700px|thumb|center]] |
| + | |||
| + | [[File:prbaru2.png|800px|thumb|center]] | ||
== Video Pembahasan == | == Video Pembahasan == | ||
Maaf sedang dalam proses upload, karena internet tidak stabil upload gagal berkali-kali via youtube | Maaf sedang dalam proses upload, karena internet tidak stabil upload gagal berkali-kali via youtube | ||
Revision as of 23:13, 5 November 2019
Study-case
Studi kasus yaitu roket yang diterbangkan lalu jatuh bebas diudara menuju permukaan bumi.
Algoritma
Kasus ini dapat diselesaikan dengan metode runge-kutta, dalam studycase ini saya berusaha mencoba mencari kecepatan pada waktu tertentu (waktu yang kita inginkan). Berikut adalah langkah-langkah yang saya lakukan dalam menyelesaikan studycase ini dengan metode runge-kutta:
1. Menyusun input yang akan digunakan yaitu mulai dari gaya berat, nilai gravitasi, koefisien drag, massa roket, dan area roket.
2. Membuat pendefinisian dari setiap nilai persamaan sesuai dengan persamaan matematis yang telah dibuat, pendefinisian berupa suatu persamaan diferensial.
3. Untuk mendapatkan nilai waktu maka runge kutta harus dibuat suatu sistem iterasi yaitu dengan menggunakan while, sehingga terjadi iterasi sampai kecepatan 0 dan diperoleh waktunya.
4. menggunakan f(t,v) sebagai fungsi (x,y) dimana t diposisikan sebagai x dan v diposisikan sebagai y.
5. menggunakan persamaan sebagai dasar runge-kutta f(t, v):((m*g-cd*v**1.5)/m)
FlowChart
Coding
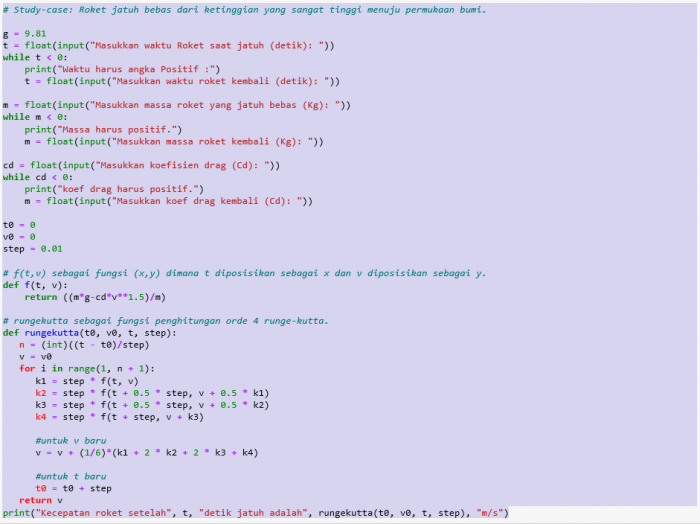
- Study-case: Roket jatuh bebas dari ketinggian yang sangat tinggi menuju permukaan bumi.
g = 9.81 t = float(input("Masukkan waktu Roket saat jatuh (detik): ")) while t < 0:
print("Waktu harus angka Positif :")
t = float(input("Masukkan waktu roket kembali (detik): "))
m = float(input("Masukkan massa roket yang jatuh bebas (Kg): ")) while m < 0:
print("Massa harus positif.")
m = float(input("Masukkan massa roket kembali (Kg): "))
cd = float(input("Masukkan koefisien drag (Cd): ")) while cd < 0:
print("koef drag harus positif.")
m = float(input("Masukkan koef drag kembali (Cd): "))
t0 = 0 v0 = 0 step = 0.01
- f(t,v) sebagai fungsi (x,y) dimana t diposisikan sebagai x dan v diposisikan sebagai y.
def f(t, v):
return ((m*g-cd*v**1.5)/m)
- rungekutta sebagai fungsi penghitungan orde 4 runge-kutta.
def rungekutta(t0, v0, t, step):
n = (int)((t - t0)/step)
v = v0
for i in range(1, n + 1):
k1 = step * f(t, v)
k2 = step * f(t + 0.5 * step, v + 0.5 * k1)
k3 = step * f(t + 0.5 * step, v + 0.5 * k2)
k4 = step * f(t + step, v + k3)
#untuk v baru
v = v + (1/6)*(k1 + 2 * k2 + 2 * k3 + k4)
#untuk t baru
t0 = t0 + step
return v
print("Kecepatan roket setelah", t, "detik jatuh adalah", rungekutta(t0, v0, t, step), "m/s")
Video Pembahasan
Maaf sedang dalam proses upload, karena internet tidak stabil upload gagal berkali-kali via youtube