Difference between revisions of "Ales Daniel"
Alesdaniel (talk | contribs) (→Permodelan Persamaan Rudal Yang Meluncur) |
Alesdaniel (talk | contribs) (→Permodelan Persamaan Rudal Yang Meluncur) |
||
| Line 175: | Line 175: | ||
dx/dt = (ax-(cd*v**3/2)/m)/cos(alpha) | dx/dt = (ax-(cd*v**3/2)/m)/cos(alpha) | ||
| + | |||
| + | Algoritma : | ||
| + | |||
| + | ''Sumbu X'' : | ||
| + | |||
| + | from math import * | ||
| + | |||
| + | g = 9.81 | ||
| + | |||
| + | m = eval(input("Massa rudal dalam kg: ")) | ||
| + | |||
| + | sudut = eval(input("Sudut kemiringan rudal dalam derajat: ")) | ||
| + | |||
| + | a = eval(input("Percepatan yang diinginkan: ")) | ||
| + | |||
| + | cd = eval(input("Koefisien hambat udara: ")) | ||
| + | |||
| + | alpha = sudut*0.0174 | ||
| + | |||
| + | ay = a*(sin(alpha)) | ||
| + | |||
| + | ax = a*(cos(alpha)) | ||
| + | |||
| + | v0 = 0 | ||
| + | |||
| + | x0 = 0 | ||
| + | |||
| + | t0 = 0 | ||
| + | |||
| + | dt = 0.1 | ||
| + | |||
| + | error = 100 | ||
| + | |||
| + | lst = [] | ||
| + | |||
| + | def dxdt(t0, v0): | ||
| + | |||
| + | return ((ax-(cd*v0**3/2)/m)) | ||
| + | |||
| + | while error > 0.005: | ||
| + | |||
| + | k1 = dt*dxdt(t0, v0) | ||
| + | |||
| + | k2 = dt*dxdt(t0+0.5*dt, v0+0.5*dt*k1) | ||
| + | |||
| + | k3 = dt*dxdt(t0+0.5*dt, v0+0.5*dt*k2) | ||
| + | |||
| + | k4 = dt*dxdt(t0+dt, v0+k3*dt) | ||
| + | |||
| + | v1 = v0 + (1/6)*(k1+2*k2+2*k3+k4) | ||
| + | |||
| + | x0 = x0 + dt | ||
| + | |||
| + | v0 = v1 | ||
| + | |||
| + | error = ((v1-v0)/v1) | ||
| + | |||
| + | lst.append(1) | ||
| + | |||
| + | #dihasilkan perhitungan untuk sumbu X | ||
| + | |||
| + | print('Kecepatan yang dihasilkan rudal pada sumbu x adalah', v1, 'm/s') | ||
| + | |||
| + | |||
| + | ''Sumbu Y'' : | ||
| + | |||
| + | from math import * | ||
| + | |||
| + | g = 9.81 | ||
| + | |||
| + | m = eval(input("Massa rudal dalam kg: ")) | ||
| + | |||
| + | sudut = eval(input("Sudut kemiringan rudal dalam derajat: ")) | ||
| + | |||
| + | a = eval(input("Percepatan yang diinginkan: ")) | ||
| + | |||
| + | cd = eval(input("Koefisien hambat udara: ")) | ||
| + | |||
| + | alpha = sudut*0.0174 | ||
| + | |||
| + | ay = a*(sin(alpha)) | ||
| + | |||
| + | ax = a*(cos(alpha)) | ||
| + | |||
| + | v0 = 0 | ||
| + | |||
| + | x0 = 0 | ||
| + | |||
| + | t0 = 0 | ||
| + | |||
| + | dt = 0.1 | ||
| + | |||
| + | error = 100 | ||
| + | |||
| + | lst = [] | ||
| + | |||
| + | def dydt(t0, v0): | ||
| + | |||
| + | return ((ay-(g*(cd*v0**3/2)/m))) | ||
| + | |||
| + | while error > 0.005: | ||
| + | |||
| + | k1 = dt*dydt(t0, v0) | ||
| + | |||
| + | k2 = dt*dydt(t0+0.5*dt, v0+0.5*dt*k1) | ||
| + | |||
| + | k3 = dt*dydt(t0+0.5*dt, v0+0.5*dt*k2) | ||
| + | |||
| + | k4 = dt*dydt(t0+dt, v0+k3*dt) | ||
| + | |||
| + | v1 = v0 + (1/6)*(k1+2*k2+2*k3+k4) | ||
| + | |||
| + | x0 = x0 + dt | ||
| + | |||
| + | v0 = v1 | ||
| + | |||
| + | error = ((v1-v0)/v1) | ||
| + | |||
| + | lst.append(1) | ||
| + | #dihasilkan perhitungan untuk sumbu Y | ||
| + | |||
| + | print('Kecepatan yang dihasilkan rudal pada sumbu Y adalah', v1, 'm/s') | ||
Revision as of 22:14, 5 November 2019
NAMA : ALES DANIEL
TEMPAT, TANGGAL LAHIR : JAKARTA, 27 OKTOBER 1998
NPM : 1706036072
DOSEN :
Dr. Ir. Ahmad Indra Siswantara
Dr. Eng. Radon Dhelika, B.Eng, M.Eng
Contents
Rabu, 4 September 2019
Mengapa Saya Harus Belajar Kalkulus?
Kalkulus merupakan suatu ilmu mendasar bagi mahasiswa teknik sebagai bekal untuk melakukan perhitungan pada mata kuliah lainnya. Penggunaan ilmu tersebut dapat mengatasi permasalahan melalui perhitungan berdasarkan data yang diinformasikan. Ilmu Kalkulus lebih berfokus kepada perhitungan fungsi, turunan, integral, dan lain-lain. Pada pertemuan pertama, kami membahas salah satu penggunaan ilmu Kalkulus pada salah satu mata kuliah teknik mesin, Termodinamika. Contoh yang digunakan adalah rumus entalpi sebagai berikut :
H = U + PV
Apabila dikaitkan dengan ilmu Kalkulus, rumus tersebut dapat diturunkan menjadi rumus sebagai berikut :
dH = dU + dPV
Setelah itu, saya dijelaskan oleh pak Dai untuk setiap pelajaran yang akan dihadapi untuk selalu memulai dengan berdoa. Kami melakukan doa bersama sebelum melakukan pelajaran dan diajak oleh beliau untuk tidak pernah lupa kepada yang maha kuasa.
Metode Numerik dan Phyton
Pada mata kuliah metode numerik ini, kami menggunakan salah satu perangkat bernama Phyton. Perangkat merupakan bahasa pemrograman untuk menyusun langkah-langkah dalam menyelesaikan suatu permasalahan melalui pemberian instruksi. Perangkat ini sedang marak digunakan oleh banyak orang sebagai bahasa pemrograman dan MIT sebagai salah satu perguruan tinggi yang tengah menggunakan perangkat lunak tersebut. Komputer sendiri tidak akan mengalami kelelahan apabila menghitung angka yang banyak. Kita harus membuat langkah-langkah menyelesaikan solusinya. Dikarenakan langkah-langkah yang panjang, diperlukan perubahan bahasa yang dimengerti oleh komputer. Bahasa yang biasanya kita mengerti akan diubah melalui interpreter menjadi bahasa mesin oleh komputer atau biasa disebut sebagai High Level Language. Melalui perangkat Phyton, model matematis sesulit apapun dengan High level language, dapat dipecahkan dengan persamaan aljabar dari suatu numerik. Dalam suatu metode numerik, pasti terdapat persamaan-persamaan didalamnya. Misalkan persamaan berikut:
A = B + C
Pernyataan tersebut pada dasaranya tidak eksak sama sekali dan yang eksak hanyalah 'The One and Only', Tuhan. Persamaan tersebut memiliki bentuk yang lebih tepat sebagai berikut :
R = A - (B + C)
R merupakan residu dengan besaran yang mendekati 0
Melalui programming tersebut, dapat diaktualisasikan pada kenyataan dengan metode numerik. Salah satu contohnya adalah prediksi badai yang akan datang sehingga masyarakat dapat melakukan evakuasi terlebih dahulu. Hal tersebut disebut dengan Weather Forecasting dan menggunakan model matematika yang sangat rumit disertai super komputer. Komputer hanya mengetahui operasi matematis tambah(+), bagi(:), kali(x), dan kurang(-). Komputer tidak mengetahui operasi integral dan hanya kita sendiri yang dapat memahaminya serta menyusunnya. Langkah-langkah instruksi tersebut disebut sebagai algoritma. Hal tersebut dapat dibantu dengan membentuk flowchart untuk mengetahui alur perhitungannya.
Tugas 01
Rabu, 11 September 2019
Pada hari ini, kami mendapatkan materi lebih dalam mengenai metode numerik. Metode numerik belajar mengenai penyelesaian model matematika dengan menggunakan High Level Language. Permodelan komputer saat ini diperlukan oleh mahasiswa teknik mesin. Komputer memiliki sebuah database untuk menyimpan file. Contohnya adalah sebuah file game catur yang menyimpan langkah-langkah. Metode numerik saat ini juga digunakan untuk Artificial Intelligence. Misalkan juga pada saat melakukan pencarian di internet, akan muncul pencarian dan hal-hal yang kita inginkan berdasarkan history yang sudah ada.
Saat sedang mendownload suatu software, kita diberikan pilihan pilihan bit antara 32 dan 64 bit. 32 bit berarti intergernya berada pada tingkat 2^31, kemudian untuk 64 bit prosesnya akan lebih berbeda. Prosesor tersebut juga memiliki batas. Misalkan, pada 32 bit, berarti batas bawah dan atas yang direpresentasikan pada komputer hanya di dalam angka tersebut. Apabila kita menjalankan suatu proses yang lebih dari 32 bit, akan terjadi overflow. Untuk mempresentasikannya diberikan bilangan biner, yaitu terdiri dari 0 dan 1. Huruf yang muncul pada komputer kita terdiri dari bilangan biner tersebut. Dalam memori, ada yang menampung data dalam bentuk angka biner. Jika dengan 64 bit, angka menghasilkan angka yang lebih besar sehingga lebih akurat dengan kualitas lebih baik.
Komputer memiliki otak berupa memori. Manusia hanya memiliki memori terbatas. Akan tetapi, manusia memiliki hati. Menurut pak Dai, berpikir yang sesungguhnya adalah menggunakan hati. Otak kita hanyalah seperti komputer sebagai penyimpan memori atau database. Kita juga harus mengetahui keterbatasan kita. Apa yang dimiliki oleh komputer hanyalah Artificial Intelligence. Yang ada pada manusia merupakan natural. Manusia sendirilah yang memiliki pure inteligence walaupun memiliki memori yang terbatas.
Pada akhir pertemuan, kami diberikan latihan soal sebagai berikut :
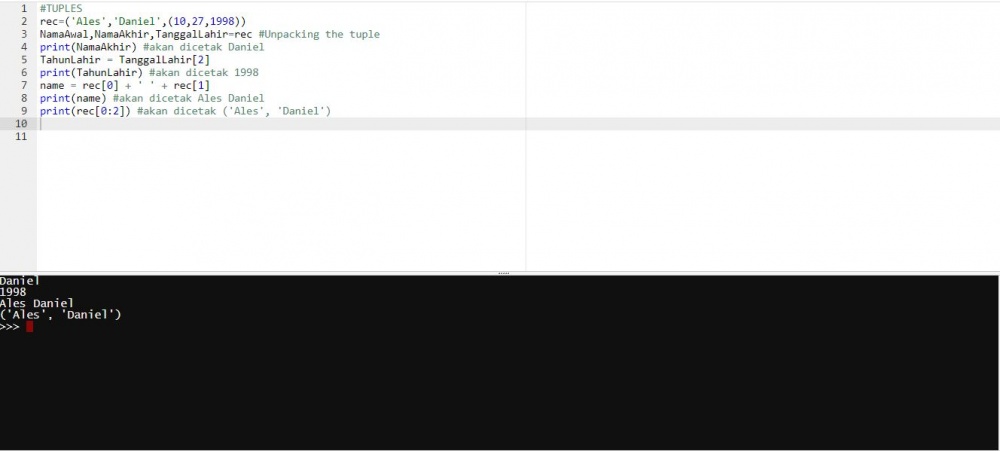
TUPLES
rec=('Ales','Daniel',(10,27,1998))
NamaAwal,NamaAkhir,TanggalLahir=rec #Unpacking the tuple
print(NamaAkhir) #akan dicetak Daniel
TahunLahir = TanggalLahir[2]
print(TahunLahir) #akan dicetak 1998
name = rec[0] + ' ' + rec[1]
print(name) #akan dicetak Ales Daniel
print(rec[0:2]) #akan dicetak ('Ales', 'Daniel')
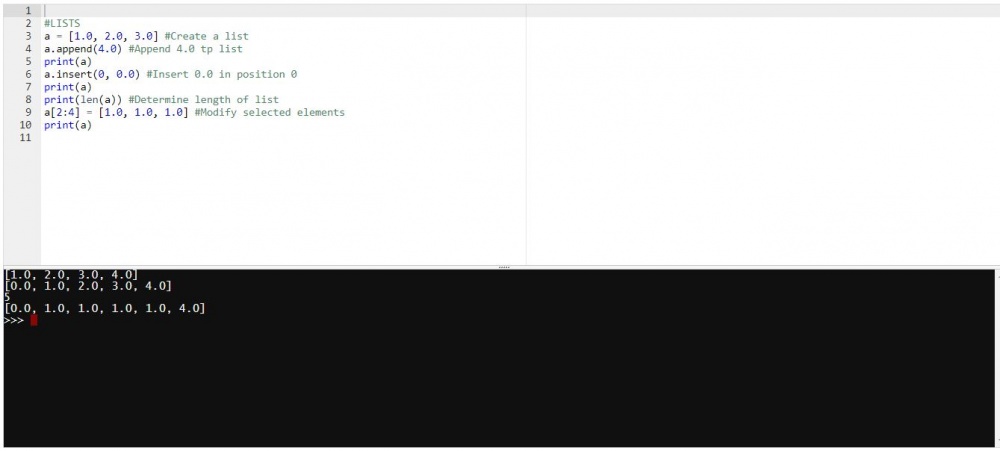
LISTS
a = [1.0, 2.0, 3.0] #Create a list
a.append(4.0) #Append 4.0 tp list
print(a)
a.insert(0, 0.0) #Insert 0.0 in position 0
print(a)
print(len(a)) #Determine length of list
a[2:4] = [1.0, 1.0, 1.0] #Modify selected elements
print(a)
Rabu, 18 September 2019
TUGAS KELOMPOK GAUSS-ELIMINATION
Rabu, 9 Oktober 2019
Seorang engineer harus memiliki skill untuk memodelkan suatu hal. Kontinuum berarti semua hal mengisi segalanya. Misalkan sebuah meja yang memiliki massa mengisi isi mejanya. Kontinuum tersebut dapat dimodelkan secara matematis dalam persamaan diferensial.
Rabu, 16 Oktober 2019
KUIS
1. Hasil Running Problem Set 2.1 No. 6
2. Hasil Running Problem Set 7.1 No. 2
x0 = 0 y = 1 h = 0.01 x = 0.03
- nilai x bisa berubah sesuai kebutuhan
def dydx(x, y):
return (x**2 - 4 * y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0) / h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai dengan x =", x, "adalah", rungeKutta(x0, y, x, h))
HASIL:
Nilai dengan x = 0.03 adalah 0.9607897700333333
UJIAN TENGAH SEMESTER; RABU, 23 OKTOBER 2019
Komentar dari teman di kanan dan kiri tempat duduk:
Permodelan Persamaan Rudal Yang Meluncur
Asumsi suatu rudal yang meluncur dengan gerakan miring dengan sudut tertentu. Rudal tersebut bergerak pada suatu posisi yang miring terhadap sumbu x dan y. Pada pengerjaan ini, rudal tersebut dianggap bergerak secara terus menerus pada kemiringan tertentu. Perhitungan yang akan dilakukan adalah turunannya terhadap sumbu x dan sumbu y. Berikut adalah permodelan matematis yang digunakan:
dy/dt = (ay-(g+(cd*v**3/2)/m)/sin(alpha)
dx/dt = (ax-(cd*v**3/2)/m)/cos(alpha)
Algoritma :
Sumbu X :
from math import *
g = 9.81
m = eval(input("Massa rudal dalam kg: "))
sudut = eval(input("Sudut kemiringan rudal dalam derajat: "))
a = eval(input("Percepatan yang diinginkan: "))
cd = eval(input("Koefisien hambat udara: "))
alpha = sudut*0.0174
ay = a*(sin(alpha))
ax = a*(cos(alpha))
v0 = 0
x0 = 0
t0 = 0
dt = 0.1
error = 100
lst = []
def dxdt(t0, v0):
return ((ax-(cd*v0**3/2)/m))
while error > 0.005:
k1 = dt*dxdt(t0, v0)
k2 = dt*dxdt(t0+0.5*dt, v0+0.5*dt*k1)
k3 = dt*dxdt(t0+0.5*dt, v0+0.5*dt*k2)
k4 = dt*dxdt(t0+dt, v0+k3*dt)
v1 = v0 + (1/6)*(k1+2*k2+2*k3+k4)
x0 = x0 + dt
v0 = v1
error = ((v1-v0)/v1)
lst.append(1)
- dihasilkan perhitungan untuk sumbu X
print('Kecepatan yang dihasilkan rudal pada sumbu x adalah', v1, 'm/s')
Sumbu Y :
from math import *
g = 9.81
m = eval(input("Massa rudal dalam kg: "))
sudut = eval(input("Sudut kemiringan rudal dalam derajat: "))
a = eval(input("Percepatan yang diinginkan: "))
cd = eval(input("Koefisien hambat udara: "))
alpha = sudut*0.0174
ay = a*(sin(alpha))
ax = a*(cos(alpha))
v0 = 0
x0 = 0
t0 = 0
dt = 0.1
error = 100
lst = []
def dydt(t0, v0):
return ((ay-(g*(cd*v0**3/2)/m)))
while error > 0.005:
k1 = dt*dydt(t0, v0)
k2 = dt*dydt(t0+0.5*dt, v0+0.5*dt*k1)
k3 = dt*dydt(t0+0.5*dt, v0+0.5*dt*k2)
k4 = dt*dydt(t0+dt, v0+k3*dt)
v1 = v0 + (1/6)*(k1+2*k2+2*k3+k4)
x0 = x0 + dt
v0 = v1
error = ((v1-v0)/v1)
lst.append(1)
- dihasilkan perhitungan untuk sumbu Y
print('Kecepatan yang dihasilkan rudal pada sumbu Y adalah', v1, 'm/s')

Enable comment auto-refresher