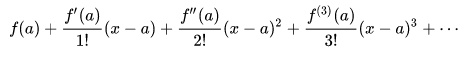Difference between revisions of "Rafi Ahmad Eshandra"
Rafieshandra (talk | contribs) (→KEGIATAN DIKELAS) |
Rafieshandra (talk | contribs) (→KEGIATAN DIKELAS) |
||
| Line 149: | Line 149: | ||
[[File:21661.jpg]] | [[File:21661.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''[['''PERTEMUAN 6''']]''' | ||
| + | |||
| + | ''Selasa, 5 November 2019'' | ||
Revision as of 10:28, 12 November 2019
Nama : Rafi Ahmad Eshandra
NPM : 1706986486
Jurusan : Teknik Mesin
No HP : 082114306757
KEGIATAN DIKELAS
Assalamualaikum wr.wb
Pada bagian ini saya akan memaparkan hasil pertemuan tiap minggunya pada mata kuliah metode numerik.
Selasa, 3 September 2019
Metode Numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematika sehingga dapat dipecahkan dengan operasi perhitungan biasa.
Pada pertemuan kali ini materi yang diberikan adalah mengenai pengolahan data dengan keterbatasan kemampuan dalam menghitung. Dimana pengaplikasian
metode numerik sangat berguna dalam kehidupan sehari-hari. Karena hasil yang didapatkan akan lebih presisi dan akurat.
Materi yang diberikan pada pertemuan kali ini adalah Metode Taylor dimana metode ini berfungsi untuk mengaproksimasikan nilai dari sebuah
fungsi.
Dalam hal ini deret tersebut merupakan jumlah tak hingga dari suku pada deret.
Untuk menghitungnya digunakan dengan prinsip turunan pada sebuah titik.
Berikut adalah rumus deret taylor :
Selasa, 10 September 2019
Pertemuan ke-2 kali ini membahas tentang tingkatan bahasa komputer. Bahasa yang paling rendah dalam komputer disebut dengan bahasa binary. Bahasa
binary sendiri hanyalah angka 1 dan 0. Sementara pembelajaran yang ditujukan pada pertemuan kali ini adalah mengenai Pseudocode yang merupakan
algortima yang ditujukan untuk dibaca oleh manusia bukan oleh komputer. Ada pula beberapa pseudocode yang diajarkan dikelas diantaranya
l = r ; err = 1
suku = x
sin = suku, while err > 1e-7
ratio = -x^2/((2*1)*(2*1+1))
suku = suku*ratio
err = abs(suku/sin)
sin = sin + suku
l = l + 1
Itulah beberapa rangkuman materi yang didapatkan pada pertemuan 2 mata kuliah metode numerik
Selasa, 17 September 2019
Pada pertemuan kali ini dibahas mengenai turunan numerik, yang mana dibagi menjadi 3 yaitu maju, mundur dan center. Turunan numerik sendiri adalah
hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Penggunaan metode ini bergantung pada data yang kita inginkan, kita harus
mengidentifikasi terlebih dahulu.
Adapula beberapa rumus mengenai turunan numerik diantaranya :
Selasa, 24 September 2019
Pertemuan kali ini membahas mengenai secant, bisect, dan Newton-Raphson method. Metode-metode ini digunakan untuk pencarian pembuat 0 dari fungsi.
ketiga metode diatas dapat disebut juga dengan root finding algoritma.
1. Secant method sendiri adalah metode yang menggunakan garis secant
2. Bisect method sendiri adalah metode pencarian akar-akar untuk fungis yang terus menerus
3. Newton-Raphson method sendiri adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan.
Itu adalah beberapa metode dari root finding algoritma.
Selasa, 1 Oktober 2019
Pertemuan kali ini membahas mengenai Truncation Error, Rounding Error, Persamaan Banyak. Inti dari pelajaran pertemuan kali ini adalah tiap-tiap
software memiliki truncation error, selain itu tiap metode numerik sendiri memiliki truncaation error pula. Akan tetapi hal-hal tersebut dapat kita
perkecil dengan meshing. Meshing sendiri adalah meshing merupakan pembagian daerah yang dianalisis menjadi partisi-partisi yang sangat kecil, semakin
kecil partisi tersebut maka akan semakin akurat pula hasilnya.
Sementara rounding error adalah kesalahan perhitungan matematis atau kesalahan kuantisasi yang disebabkan oleh perubahan angka menjadi bilangan
bulat. Apabila jumlah pengoperasian perhitungan bertambah banyak maka jumlah rounding akan semakin banyak pula.
Selasa, 29 Oktober 2019
Selasa, 5 November 2019