Wahyu Nugroho Ramadhan

Pertemuan Pertama

Telapak Kaki Kalkulus

Rabu, 4 September 2019. MAhasiswa kelas Metode Numerik 02 diberi tugas membuat tulisan dengan tema mengapa kita harus belajar kalkulus

Berikut adalah tulisan saya

Kalkulus merupakan salah satu mata kuliah yang saya pelajari sata semester 1 dan 2 perkuliahan di Fakultas Teknik Universitas Indonesia. Dengan Jurusan Teknik Mesin kini sadar bahwa suatu teknologi paling mutakhir sejatinya berawal dari perhitungan yang matang. Dan kalkulus adalah pondasinya. Seperti ketika kita ingin membuat baling2 pesawat tentu kita harus tau volume benda putarnya agar ketika baling2 berputar tidak terjadi benturan dengan bagian lain. Maka dari itu bisa dibilang kalau kalkulus adalah telapak kaki anak teknik yang akan selalu digunakan untuk berjalan menyusuri dunia perkulihanan hingga pekerjaan

Pertemuan Kedua

Rabu, 11 September 2019

pada pertemuan kedua saya mempelajari fungsi variabel, string, tuplet, dan list

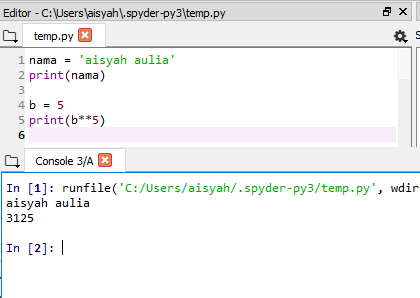
Variable Merupakan pendefinisian suatu hal menggunakan simbol misal A = 2

String Berfungi untuk menggantikan sebuah kalimat panjang menjadi lebih sederhana misal Menu1 = Nasi padang bumbu kacang menu2 = Nasi rawon bumbu kecap

Tuples adalah cara input data agar mudah di cari misal pada nama yang panjang 1. Muhammad 2. Bagus 3. Ferdinan 4. Siregar

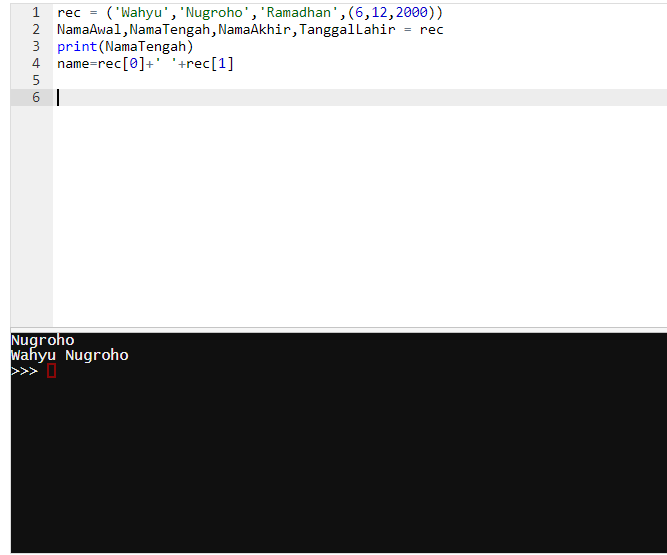
Diinput dalam rumus >>> rec("Wahyu","Nugroho","Ramadhan",(06,12,2000)

untuk membuka nama kita gunakan >>> namaDepan,namaTengah,namaBelakang,tanggalLahir=rec

hasilnya adalah kita dapat mencari kata yang dicari dengan memasukan kata kuci tiap-tiap kata misal Wahyu = namaDepan Nugroho = namaTengah Ramadhan = namaBelakang 06,12,200 = tanggalLahir

Pertemuan ketiga

Rabu, 18 September 2019

Pada pertemuan ketiga kita melakukan quiz dengan mengubah bilangan Fibonacci kedalam bahasa pemrograman pyton pada percobaan pertama kami mengerjakan tugas tanpa melihat aplikasi maupun bantuan lainnya jadi bahasa pemrograman yang kami buat di percobaan pertama murni merepresentasikan sejauh mana pengetahuan kami tentang bahsa pemrograman lalu pada percobaan kedua kami diberi clue oleh dosen, dapat membuka aplikasi, maupun bekerja sama dengan teman

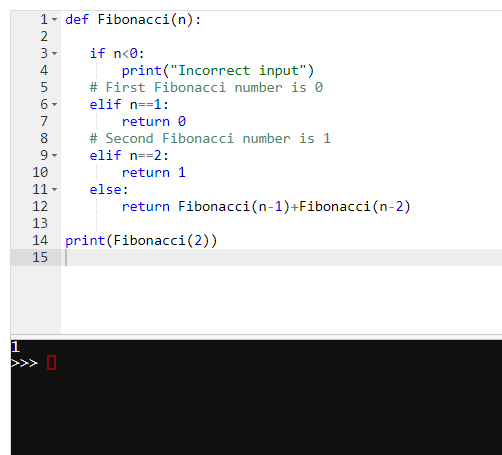
pada percobaan kedua kami diberi dua tugas yaitu membuat bahsa programnya serta flowchart

def Fibonacci(n):

   if n<0: 
       print("Incorrect input") 
   # First Fibonacci number is 0 
   elif n==1: 
       return 0
   # Second Fibonacci number is 1 
   elif n==2: 
       return 1
   else: 
       return Fibonacci(n-1)+Fibonacci(n-2) 

print(Fibonacci( ))

dengan subtitusi angka ke-n maka akan muncul Un

lalu untuk flowchartny

Pertemuan Ketujuh

membuat algoritma python unutk soal

Prolem set 2.1 hal 55

line1 = [0,0,2,1,2] line2 = [0,1,0,2,-1] line3 = [1,2,0,-2,1] line4 = [0,0,0,-1,1] line5 = [0,1,-1,1,-1]

nmat = np.array ([line1,line2,line3,line4,line5]) print ("n Matrix adalah:") print (nmat) cons = np.array ([1,1,-4,-2,-1]) print ("Matrix Y adalah:") print (cons)

jawab = linalg.solve (nmat,cons) x1value = int(jawab[0]) x2value = int(jawab[1]) x3value = int(jawab[2]) x4value = int(jawab[3]) x5value = int(jawab[4]) print ("hasil X adalah :") print ("x1= ",x1value) print ("x2= ",x2value) print ("x3= ",x3value) print ("x4= ",x4value) print ("x5= ",x5value)

Problem set 7.1 beluuuuuuuuu kelar def dydx(x, y):

   return ((x**2 - 4*y)) 
 

1. Finds value of y for a given x using step size h
2. and initial value y0 at x0.

def rungeKutta(x0, y0, x, h):

   # Count number of iterations using step size or 
   # step height h 
   n = (int)((x - x0)/h)  
   # Iterate for number of iterations 
   y = y0 
   for i in range(1, n + 1): 
       "Apply Runge Kutta Formulas to find next value of y"
       k1 = h * dydx(x0, y) 
       k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) 
       k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) 
       k4 = h * dydx(x0 + h, y + k3) 
 
       # Update next value of y 
       y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) 
 
       # Update next value of x 
       x0 = x0 + h 
   return y 
 

1. misalkan :

x0 = 0 y = 1 x = 0.03 h = 0.01 print ('The value of y at x is:', rungeKutta(x0, y, x, h))