Dwiko Arief Wicaksono

Biografi

Dwiko Arief Wicaksono, lahir pada tanggal 22 Juni 1997 di Batam; tumbuh besar di daerah Tanjung Priok, Jakarta Utara sampai dengan umur 6 tahun. Setelah itu, ia pindah ke Cikarang, Bekasi dan menempuh pendidikan dasar di SD Al - Azhar 12 Cikarang. Dilanjutkan dengan pendidikan menengah pertama pada SMP Al - Azhar 16 Cikarang. Pendidikan menegah atas Dwiko dilanjutkan di Bogor, tepatnya pada sekolah asrama yang mempunyai nama SMA Dwiwarna. Setelah lulus SMA Dwiko melanjutkan pendidikannya di salah satu perguruan tinggi negeri, yaitu Universitas Indonesia melalui jalur SIMAK dan masuk ke jurusan Teknik Sipil.

Metode Numerik

Konstribusi Python dalam kalkulasi matematika dapat dilihat pada kegunaannya dalam penyelesaian persamaan linear. Sebelum masuk ke dalam kalkulasi persamaan linear, terdapat dasar-dasar kalkulasi pada bahasa pemrograman Python yang harus dikuasai terlebih dahulu, dasar-dasar Python sebagai berikut,

Variables

Pada bahasa pemrogaman ini, pengguna harus memberikan argumen pada variabel yang akan dikalkulasikan, berikut contohnya,

>>>b = 2

>>>print (b)

dari command diatas, akan muncul hasil seperti berikut,

2

untuk kalkulasi matematika sederhana dengan menggunakan 2 variabel, pengguna harus memberikan argumen terhadap 2 variabel tersebut,

>>>a = 3

>>>b = 2

>>>print (a*b)

maka hasil yang muncul adalah

6

command diatas dapat dituliskan dengan cara lain seperti,

>>>a = 3

>>>b = 2

>>>c = a * b

>>>print (c)

6

Tugas rangkaian pipa

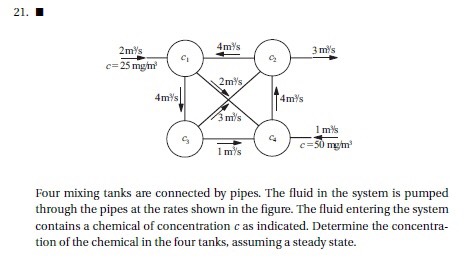
Dari soal diatas, dengan menggunakan hokum kontinuitas maka akan didapatkan persamaan sebagai berikut,

6C1 - 4C2 + 0C3 + 0C4 = 50 
-2C1 + 0C2 - 1C3 + 4C4 = 50 
0C1 + 7C2 - 3C3 - 4C4 = 0 
-4C1 + 0C2 + 4C3 + 0C4 = 0 

Persamaan itu selanjutnya akan dieliminsasi menggunakan metode gauss dengan bentuk matrix sebagai berikut,

6  -4  0  0 | 50
-2  0  -1  4 | 50
0  7  -3  -4 | 0
-4  0  4  0 | 0

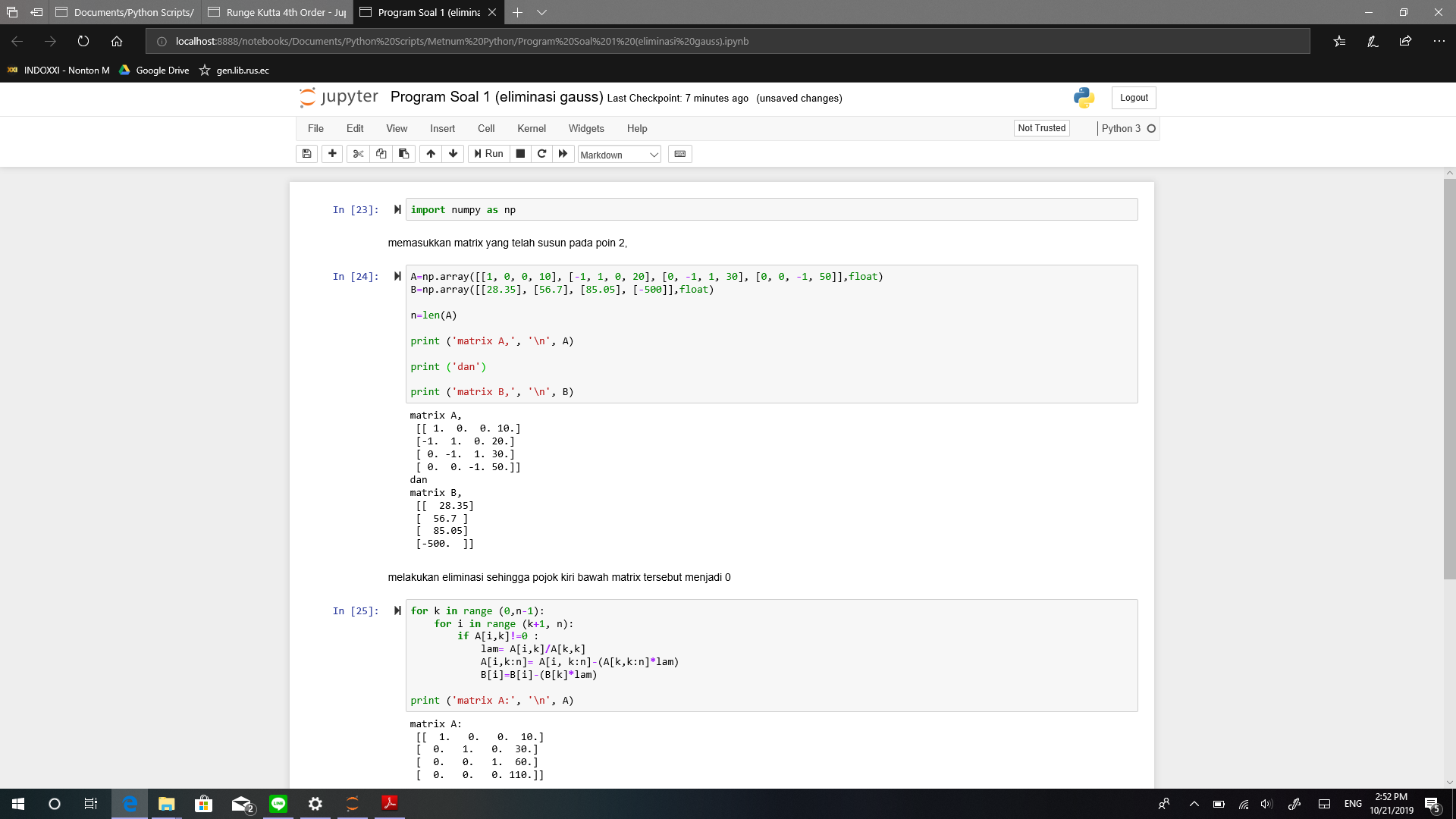
setelah itu, dimasukkan ke dalam kode python yang telah dibuat sebelumnya

KUIS

Problem set 2.1 Nomor 6 halaman 55

Pada soal ini matrix yang diberikan soal adalah sebagai berikut,

A = [[0, 0, 2, 1, 2], [0, 1, 0, 2, -1], [1, 2, 0, -2, 0], [0, 0, 0, -1, 1], [0, 1, -1, 1, -1]]

B = [1, 1, -4, -2, -1]

sebelum memasuki eleminasi gauss, matrix tersebut harus dikonfigurasi ulang agar bisa dihitung,

konfigurasi matrix,

A = [[1, 2, 0, -2, 0], [0, 1, 0, 2, -1],[0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]]

B = [-4, 1, -1, -2, 1]

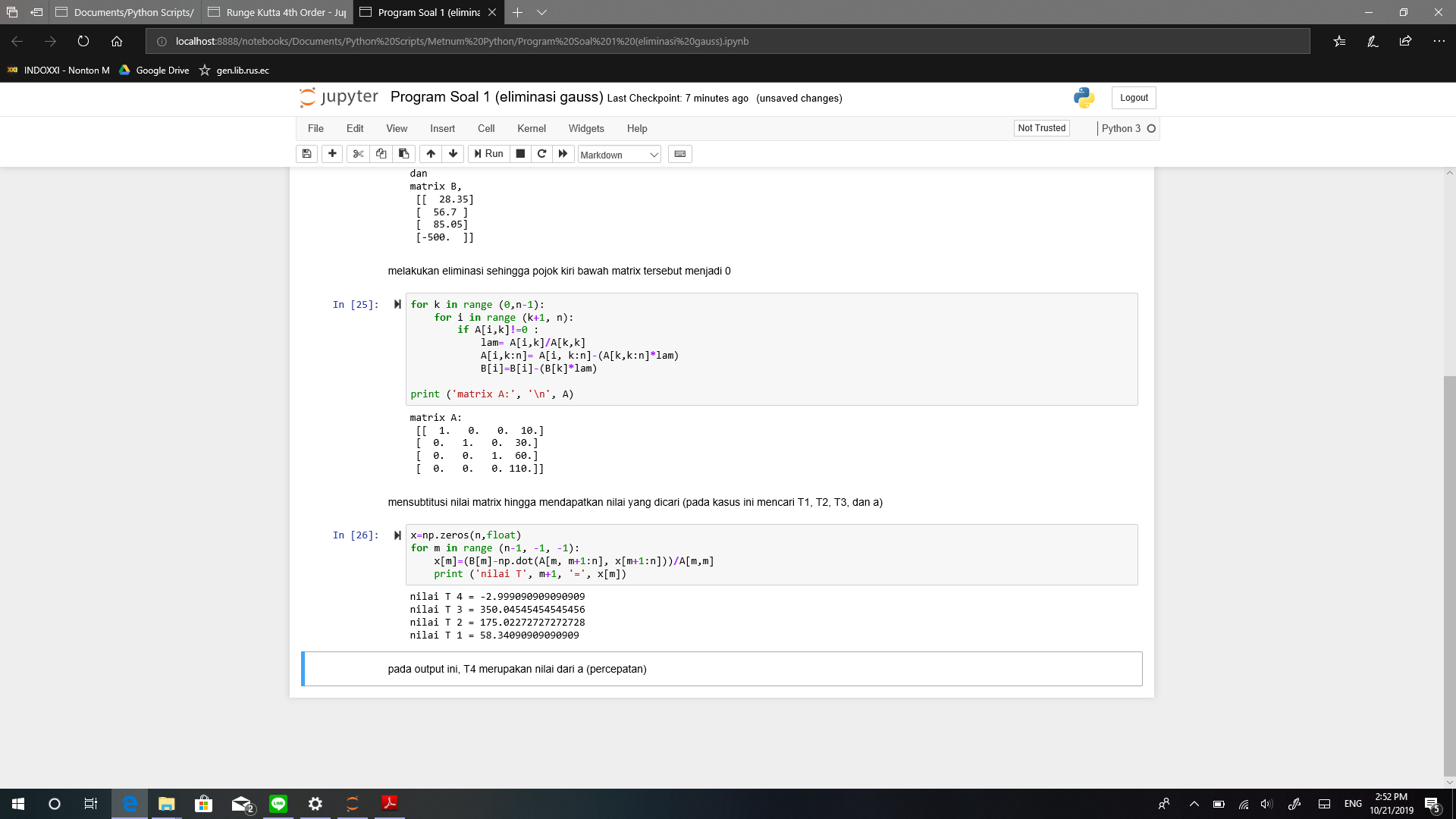
maka hasil yang akan didapatkan adalah,

X1 = 2

X2 = -2

X3 = 1

X4 = 1

X5 = -1

kode python

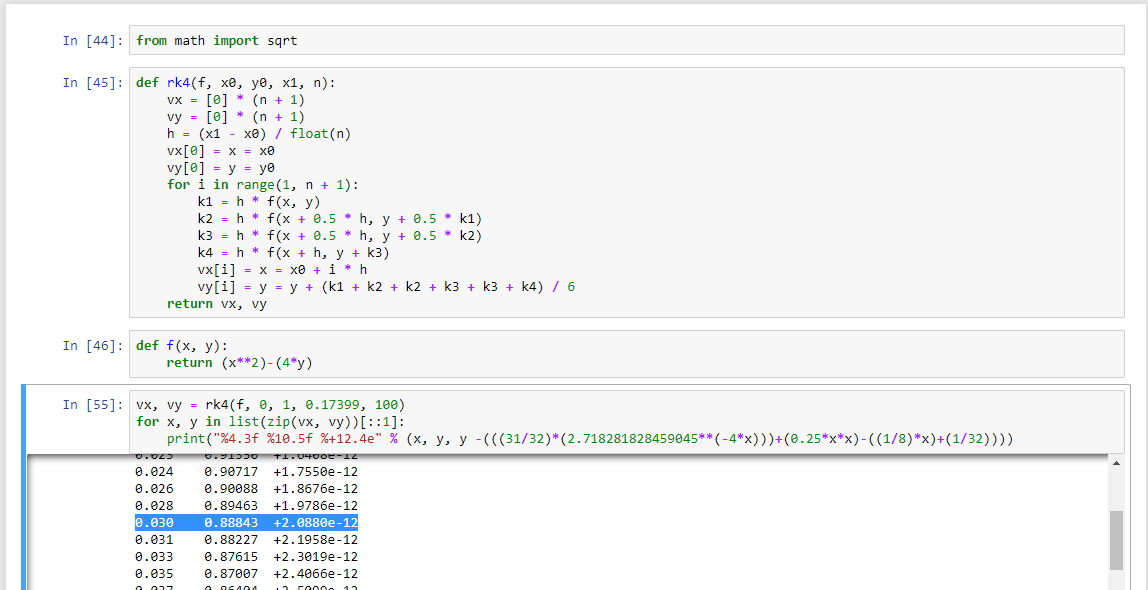
Problem set 7.1 No 1 halaman 263

hasil tersebut memiliki error dari rumus analitis sebesar +2.0880e-12

UTS

soal 1 (eliminasi gauss)

Asumsi yang digunakan,

m1 = 10 kg

m2 = 20 kg

m3 = 30 kg

m4 = 50 kg

sudut = 30

gravitasi = 10 m/s2

konstanta gesek 1 = konstanta gesek 2 = konstanta gesek 3 = 0.25