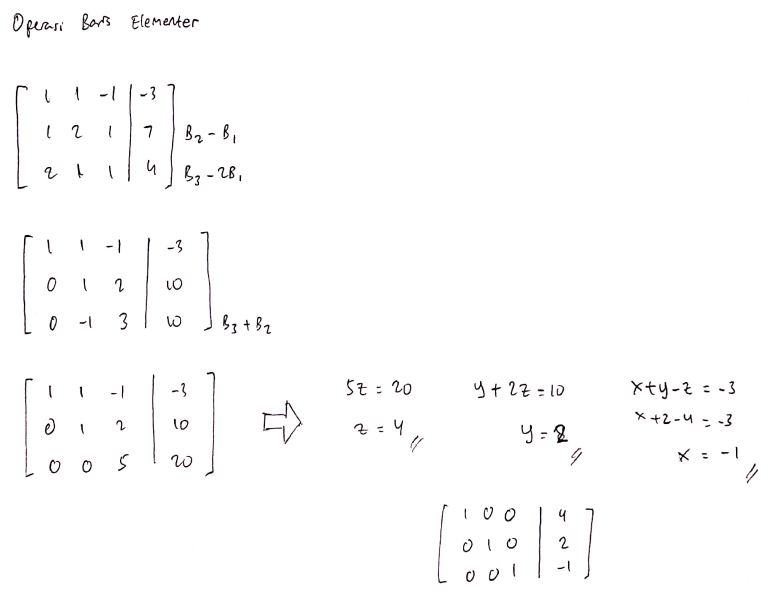Difference between revisions of "Kelompok 14"
| Line 53: | Line 53: | ||
[[File:K14-metnum_gauss-jordan.mp4]] | [[File:K14-metnum_gauss-jordan.mp4]] | ||
| + | |||
| + | |||
| + | |||
| + | == Menyelesaikan Soal dengan Runge-Kutta == | ||
| + | |||
| + | [[File:K14-Runge_kutta_2.png]] | ||
| + | |||
| + | === Algoritma === | ||
| + | |||
| + | === Flowchart === | ||
| + | |||
| + | === Kode di python === | ||
| + | |||
| + | # x0 dan y sebagai titik asal, x sebagai t yang diinput, dan h sebagai tingkat peningkatan, di sini digunakan h = 0.001 supaya cukup akurat | ||
| + | x0 = 0 | ||
| + | y = 0 | ||
| + | h = 0.001 | ||
| + | x = float(input("Nilai t: ")) # perintah untuk memasukkan nilai t sebagai x | ||
| + | |||
| + | if 0 <= x < 2: # untuk 0 <= t < 2 | ||
| + | def dydx(x, y): # dydx menyatakan persamaan awal dalam soal | ||
| + | return (4 * x - 30 * y) # diperoleh 4x - 30y karena diketahui di soal m = 2,5 kg dan k = 75 N/m, P(t) dinyatakan dalam x | ||
| + | |||
| + | def rungeKutta(x0, y0, x, h): # perhitungan Runge-Kutta | ||
| + | n = (int)((x - x0) / h) | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | k1 = h * dydx(x0, y) | ||
| + | k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * dydx(x0 + h, y + k3) | ||
| + | y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | x0 = x0 + h | ||
| + | return y | ||
| + | |||
| + | print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h)) | ||
| + | |||
| + | elif x >= 2: # untuk t > 2 | ||
| + | def dydx(x, y): # dydx menyatakan persamaan awal dalam soal | ||
| + | return (8 - 30 * y) # diperoleh 8 - 30y karena diketahui di soal P(t) = 20 N , m = 2,5 kg , k = 75 N/m | ||
| + | |||
| + | def rungeKutta(x0, y0, x, h): # perhitungan Runge-Kutta | ||
| + | n = (int)((x - x0) / h) | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | k1 = h * dydx(x0, y) | ||
| + | k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * dydx(x0 + h, y + k3) | ||
| + | y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | x0 = x0 + h | ||
| + | return y | ||
| + | |||
| + | print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h)) # print nilai y pada t yang diinput | ||
| + | |||
| + | else: | ||
| + | print("Nilai t harus positif.") # memberitahu nilai t harus positif jika t yang dimasukkan negatif | ||
| + | |||
| + | [[File:K14-Runge_kutta.png]] | ||
| + | |||
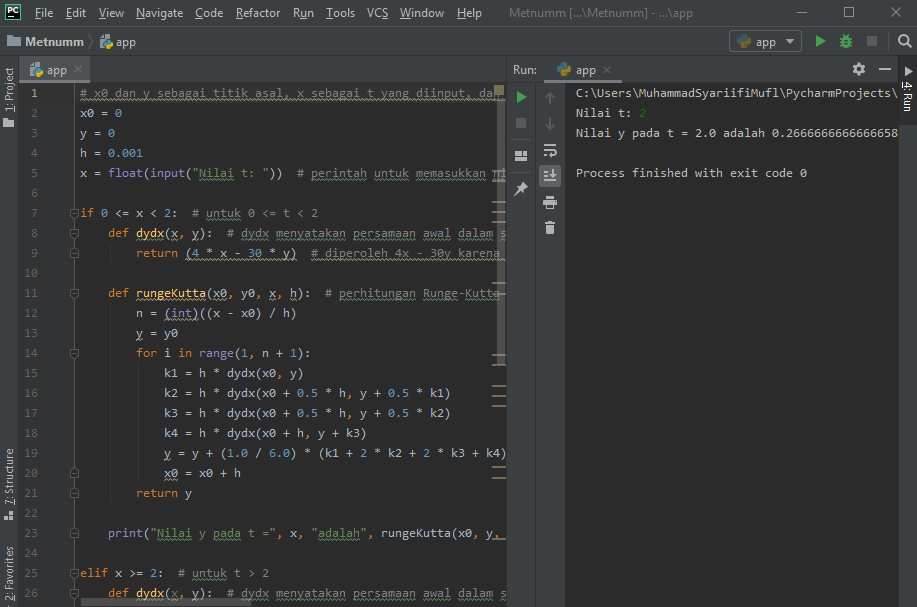
| + | Run dari kode di atas, ketika dimasukkan t = 2, program menampilkan nilai y pada t = 2 yaitu 0.2666666666666658 | ||
Revision as of 15:28, 16 October 2019
Contents
Anggota Kelompok 14
Muhammad Syariifi Muflih (1806149210)
Fabio Almer Agoes (1806201296)
Oimolala Putrawan (1706036412)
Eliminasi Gauss-Jordan
Pengertian
Eliminasi Gauss-Jordan adalah prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks eselon baris tereduksi dengan metode operasi baris elementer.
Contoh soal:
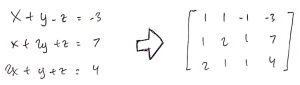
x + y – z = –3
x + 2y + z = 7
2x + y + z = 4
Pertama, sistem persamaan linear yang ingin dipecahkan diubah ke matriks:
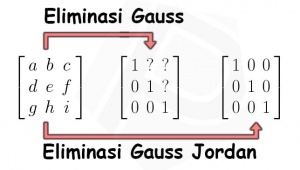
Kemudian, dengan operasi baris elementer, matriks tersebut diubah menjadi matriks eselon baris (gauss), kemudian diubah lagi menjadi matriks eselon baris tereduksi (gauss-jordan).
Berikut penyelesaian secara manual:
Menyelesaikan SPL dengan Eliminasi Gauss-Jordan menggunakan Python
Contoh soal sistem persamaan linear 3 variabel:
x + y – z = –3
x + 2y + z = 7
2x + y + z = 4
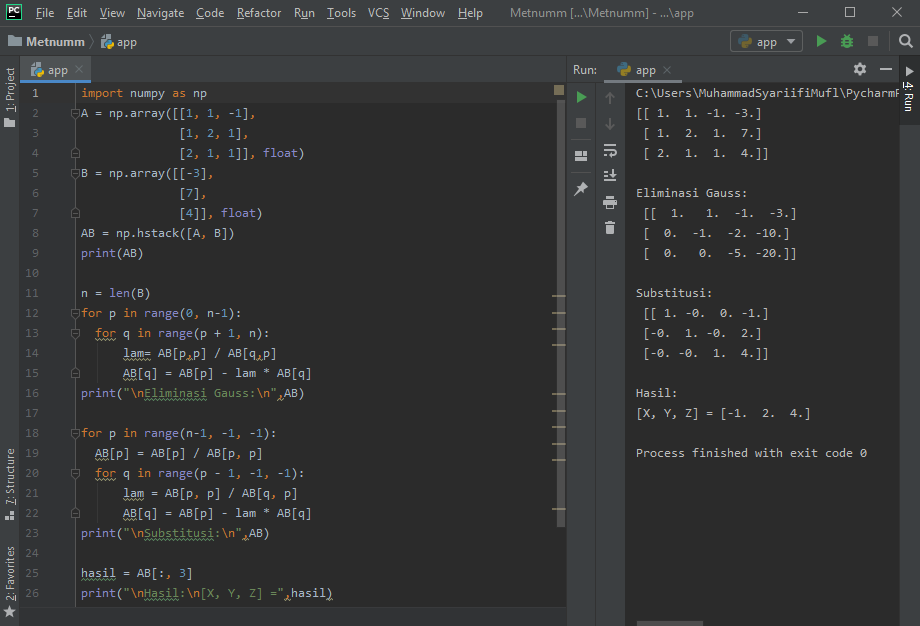
Berikut kode yang kami gunakan di python:
Video
Menyelesaikan Soal dengan Runge-Kutta
Algoritma
Flowchart
Kode di python
# x0 dan y sebagai titik asal, x sebagai t yang diinput, dan h sebagai tingkat peningkatan, di sini digunakan h = 0.001 supaya cukup akurat
x0 = 0
y = 0
h = 0.001
x = float(input("Nilai t: ")) # perintah untuk memasukkan nilai t sebagai x
if 0 <= x < 2: # untuk 0 <= t < 2
def dydx(x, y): # dydx menyatakan persamaan awal dalam soal
return (4 * x - 30 * y) # diperoleh 4x - 30y karena diketahui di soal m = 2,5 kg dan k = 75 N/m, P(t) dinyatakan dalam x
def rungeKutta(x0, y0, x, h): # perhitungan Runge-Kutta
n = (int)((x - x0) / h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 2: # untuk t > 2
def dydx(x, y): # dydx menyatakan persamaan awal dalam soal
return (8 - 30 * y) # diperoleh 8 - 30y karena diketahui di soal P(t) = 20 N , m = 2,5 kg , k = 75 N/m
def rungeKutta(x0, y0, x, h): # perhitungan Runge-Kutta
n = (int)((x - x0) / h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h)) # print nilai y pada t yang diinput
else:
print("Nilai t harus positif.") # memberitahu nilai t harus positif jika t yang dimasukkan negatif
Run dari kode di atas, ketika dimasukkan t = 2, program menampilkan nilai y pada t = 2 yaitu 0.2666666666666658