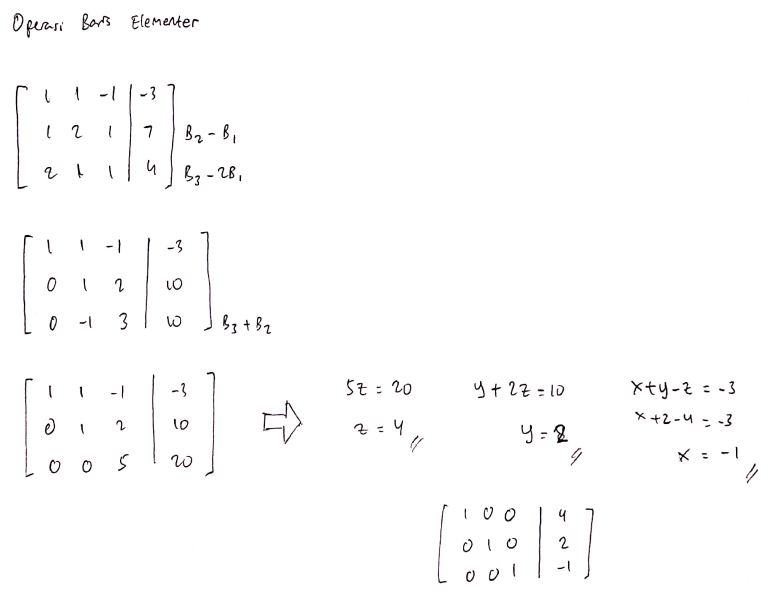Difference between revisions of "Kelompok 14"
| Line 12: | Line 12: | ||
=== Pengertian === | === Pengertian === | ||
| − | Eliminasi Gauss-Jordan adalah prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks '''eselon baris tereduksi''' dengan ''' | + | Eliminasi Gauss-Jordan adalah prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks '''eselon baris tereduksi''' dengan metode '''operasi baris elementer'''. |
Contoh soal: | Contoh soal: | ||
| Line 24: | Line 24: | ||
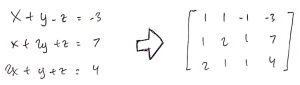
Pertama, sistem persamaan linear yang ingin dipecahkan diubah ke matriks: | Pertama, sistem persamaan linear yang ingin dipecahkan diubah ke matriks: | ||
| − | [[File:K14-mengubah_spl_ke_matriks.png]] | + | [[File:K14-mengubah_spl_ke_matriks.png|thumb|center]] |
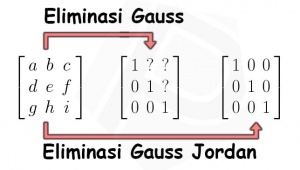
Kemudian, dengan operasi baris elementer, matriks tersebut diubah menjadi matriks eselon baris '''(gauss)''', kemudian diubah lagi menjadi matriks eselon baris tereduksi '''(gauss-jordan)'''. | Kemudian, dengan operasi baris elementer, matriks tersebut diubah menjadi matriks eselon baris '''(gauss)''', kemudian diubah lagi menjadi matriks eselon baris tereduksi '''(gauss-jordan)'''. | ||
| − | [[File:K14-Ilustrasi-eliminasi-gauss-jordan.jpg]] | + | [[File:K14-Ilustrasi-eliminasi-gauss-jordan.jpg|thumb|center]] |
Berikut penyelesaian secara manual: | Berikut penyelesaian secara manual: | ||
| Line 50: | Line 50: | ||
[[File:K14-gauss-jordan elimination.png]] | [[File:K14-gauss-jordan elimination.png]] | ||
| − | + | ||
| + | |||
| + | [[File:K14-metnum_gauss-jordan.mp4]] | ||
Revision as of 21:26, 15 October 2019
Contents
Anggota Kelompok 14
Muhammad Syariifi Muflih (1806149210)
Fabio Almer Agoes (1806201296)
Oimolala Putrawan (1706036412)
Eliminasi Gauss-Jordan
Pengertian
Eliminasi Gauss-Jordan adalah prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks eselon baris tereduksi dengan metode operasi baris elementer.
Contoh soal:
x + y – z = –3
x + 2y + z = 7
2x + y + z = 4
Pertama, sistem persamaan linear yang ingin dipecahkan diubah ke matriks:
Kemudian, dengan operasi baris elementer, matriks tersebut diubah menjadi matriks eselon baris (gauss), kemudian diubah lagi menjadi matriks eselon baris tereduksi (gauss-jordan).
Berikut penyelesaian secara manual:
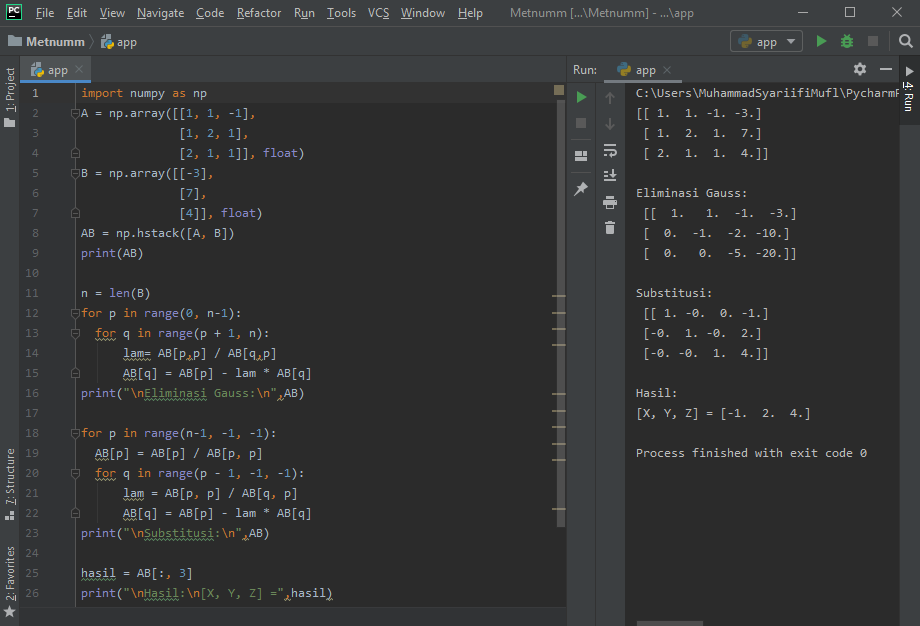
Menyelesaikan SPL dengan Eliminasi Gauss-Jordan menggunakan Python
Contoh soal sistem persamaan linear 3 variabel:
x + y – z = –3
x + 2y + z = 7
2x + y + z = 4
Berikut kode yang kami gunakan di python: