Difference between revisions of "Yarynara Sebrio. S"
(→Tugas Metode Numerik) |
(→tugas 1) |
||
| Line 21: | Line 21: | ||
x1 = 0 | x1 = 0 | ||
| + | |||
dx1 = ('0.1') | dx1 = ('0.1') | ||
| + | |||
dx = float (dx1) | dx = float (dx1) | ||
| + | |||
x2 = x1+dx | x2 = x1+dx | ||
| + | |||
Fx_1 = ((x2**2)-1) / (x1-1) | Fx_1 = ((x2**2)-1) / (x1-1) | ||
| + | |||
n = 1 error = 0 | n = 1 error = 0 | ||
| + | |||
print ("n x F(x) error") | print ("n x F(x) error") | ||
| + | |||
print (n," ",x1," ",Fx_1," ",error) | print (n," ",x1," ",Fx_1," ",error) | ||
| + | |||
while x2<1 : | while x2<1 : | ||
| + | |||
Fx_2 = ((x2**2)-1) / (x2-1) | Fx_2 = ((x2**2)-1) / (x2-1) | ||
| + | |||
error = ((Fx_2-Fx_1) / Fx_1) | error = ((Fx_2-Fx_1) / Fx_1) | ||
| + | |||
Fx_1 = Fx_2 | Fx_1 = Fx_2 | ||
| + | |||
n = n+1 | n = n+1 | ||
| + | |||
print (n," ",x1," ",Fx_1," ",error) | print (n," ",x1," ",Fx_1," ",error) | ||
| + | |||
x2=x2+dx | x2=x2+dx | ||
Revision as of 09:50, 14 October 2019
Biografi
Nama : Yarynara Sebrio Suharyadi
TTL : Jakarta,23 September 1999
NPM : 1706070816
Jurusan : Teknik Mesin Paralel Universitas Indonesia
Hobi : Bermain Tenis lapangan
Di bagian pemograman python ini saya mempelajari cara mengerjakan operasi matematika yang sering digunakan untuk membuat simulasi di berbagai sistem seperti fisika,kimia,biologi , cara menyelesaikan matematika tersebut cukup sulit diperoleh karena persamaan disamping yang tidak efisien
Tugas Metode Numerik
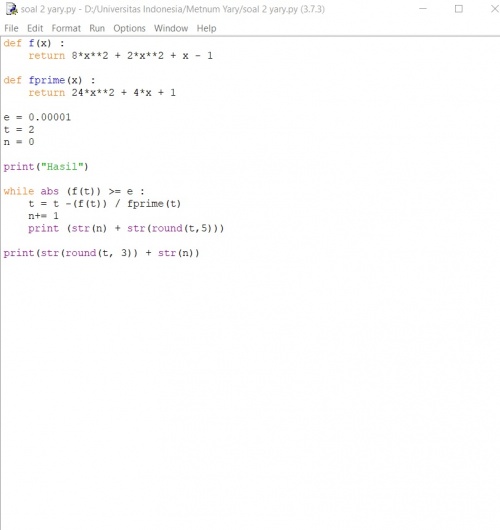
tugas 1
x1 = 0
dx1 = ('0.1')
dx = float (dx1)
x2 = x1+dx
Fx_1 = ((x2**2)-1) / (x1-1)
n = 1 error = 0
print ("n x F(x) error")
print (n," ",x1," ",Fx_1," ",error)
while x2<1 :
Fx_2 = ((x2**2)-1) / (x2-1)
error = ((Fx_2-Fx_1) / Fx_1)
Fx_1 = Fx_2
n = n+1
print (n," ",x1," ",Fx_1," ",error)
x2=x2+dx
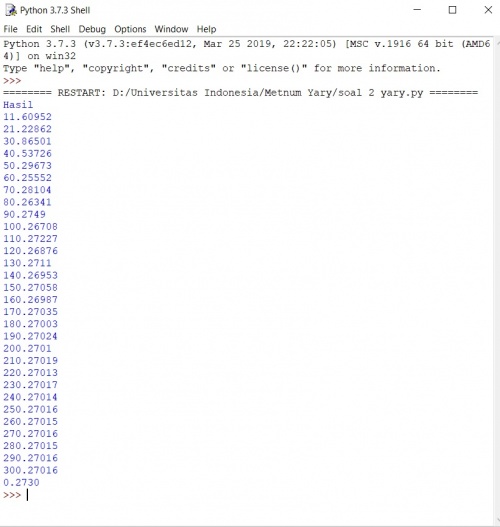
Tugas 2
Tugas 3
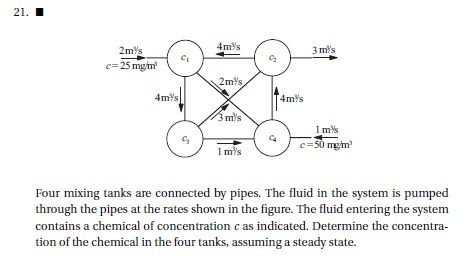
Soal ini dikerjakan dengan menggunakan Hukum Kontinuitas Massa Definisi : massa yang masuk ke dalam sistem akan sama dengan massa yang keluar dari sistem
Rumus Q*p=Q*p
Karena terdapat 4 variabel, maka terdapat 4 persamaan
6C1 - 4C2 = 50
-2C1 - 1C3 + 4C4 = 50
7C2 - 3C3 - 4C4 = 0
-4C1 + 4C3 = 0
6C1 - 4C2 + 0C3 + 0C4 = 50
-2C1 + 0C2 - 1C3 + 4C4 = 50
0C1 + 7C2 - 3C3 - 4C4 = 0
-4C1 + 0C2 + 4C3 + 0C4 = 0
Dari model python akan didapatkan nilai
C1 = 275/9
C2 = 100/3
C3 = 275/9
C4 = 425/12
- python segera menyusul