Difference between revisions of "Kelompok 2"
| Line 1: | Line 1: | ||
| + | ===Eliminasi Gauss=== | ||
| + | <youtube width="200" height="100">Ysrz1P3X-_s</youtube> | ||
| + | |||
Pengerjaan dilakukan menggunakan algoritma Gauss seperti yang ada di buku Phyton. Namun, yang membedakan adalah tidak menggunakan ''module'' pada pengerjaan ini. Berikut adalah algoritma yang sudah dirancang berdasarkan soal pada buku Phyton : | Pengerjaan dilakukan menggunakan algoritma Gauss seperti yang ada di buku Phyton. Namun, yang membedakan adalah tidak menggunakan ''module'' pada pengerjaan ini. Berikut adalah algoritma yang sudah dirancang berdasarkan soal pada buku Phyton : | ||
| Line 9: | Line 12: | ||
[-9], \ | [-9], \ | ||
[-5]] | [-5]] | ||
| − | |||
n = len(b) | n = len(b) | ||
for k in range(0, n-1): | for k in range(0, n-1): | ||
| Line 18: | Line 20: | ||
for f in range(0,n): | for f in range(0,n): | ||
a[i][f]=a[i][f]-op*a[i-1][f] | a[i][f]=a[i][f]-op*a[i-1][f] | ||
| − | |||
Hasil=['Hasilnya'] | Hasil=['Hasilnya'] | ||
if a[2][2] !=0: | if a[2][2] !=0: | ||
Revision as of 17:58, 7 October 2019
Eliminasi Gauss
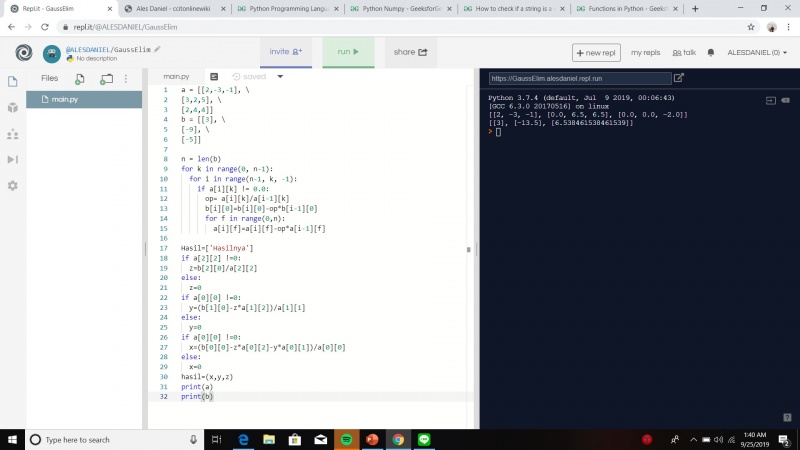
Pengerjaan dilakukan menggunakan algoritma Gauss seperti yang ada di buku Phyton. Namun, yang membedakan adalah tidak menggunakan module pada pengerjaan ini. Berikut adalah algoritma yang sudah dirancang berdasarkan soal pada buku Phyton :
Algoritma yang kami gunakan adalah sebagai berikut:
a = [[2,-3,-1], \
[3,2,5], \
[2,4,4]]
b = [[3], \
[-9], \
[-5]]
n = len(b)
for k in range(0, n-1):
for i in range(n-1, k, -1):
if a[i][k] != 0.0:
op= a[i][k]/a[i-1][k]
b[i][0]=b[i][0]-op*b[i-1][0]
for f in range(0,n):
a[i][f]=a[i][f]-op*a[i-1][f]
Hasil=['Hasilnya']
if a[2][2] !=0:
z=b[2][0]/a[2][2]
else:
z=0
if a[0][0] !=0:
y=(b[1][0]-z*a[1][2])/a[1][1]
else:
y=0
if a[0][0] !=0:
x=(b[0][0]-z*a[0][2]-y*a[0][1])/a[0][0]
else:
x=0
hasil=(x,y,z)
print(a)