Difference between revisions of "Metode Numerik soal 21 - Jaringan pipa"

From ccitonlinewiki
Jump to: navigation, search
Line 2: Line 2:
  
 
[[File:S__18382858.jpg]]
 
[[File:S__18382858.jpg]]
 +
 +
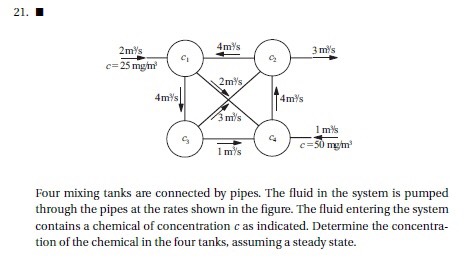
dikerjakan menggunakan hukum kontinuitas massa dimana masa yang masuk akan sama dengan yang dikeluarkan sehingga didapati rumus Q*''p''=Q*''p'' sehingga akan mendapatakan 4 persamaan dengan 4 variabel
 +
 +
 +
6C1 - 4C2 = 50
 +
 +
-2C1 - 1C3 + 4C4 = 50
 +
   
 +
7C2 - 3C3 - 4C4 = 0
 +
 +
-4C1 + 4C3 = 0
 +
 +
 +
 +
 +
6C1 - 4C2 + 0C3 + 0C4 = 50
 +
 +
-2C1 + 0C2 - 1C3 + 4C4 = 50
 +
 +
0C1 + 7C2 - 3C3 - 4C4 = 0
 +
 +
-4C1 + 0C2 + 4C3 + 0C4 = 0
 +
 +
yang kemudian dijadikan dalam modue python lalu didapatkan nilai C1 = 275/9 , C2 = 100/3 , C3 = 275/9, C4 = 425/12
 +
 +
 +
 +
<div border-style: inset;">
 +
import numpy as np
 +
class GEPP():
 +
    def __init__(self, A, b, doPricing=True):
 +
        #super(GEPP, self).__init__()
 +
        self.A = A                      # input: A is an n x n numpy matrix
 +
        self.b = b                      # b is an n x 1 numpy array
 +
        self.doPricing = doPricing
 +
        self.n = None                  # n is the length of A
 +
        self.x = None                  # x is the solution of Ax=b
 +
        self._validate_input()          # method that validates input
 +
        self._elimination()            # method that conducts elimination
 +
        self._backsub()                # method that conducts back-substitution
 +
    def _validate_input(self):
 +
        self.n = len(self.A)
 +
        if self.b.size != self.n:
 +
            raise ValueError("Invalid argument: incompatible sizes between" +
 +
                            "A & b.", self.b.size, self.n)
 +
    def _elimination(self):
 +
        """
 +
        k represents the current pivot row. Since GE traverses the matrix in the
 +
        upper right triangle, we also use k for indicating the k-th diagonal
 +
        column index.
 +
        :return
 +
        """
 +
        # Elimination
 +
        for k in range(self.n - 1):
 +
            if self.doPricing:
 +
                # Pivot
 +
                maxindex = abs(self.A[k:, k]).argmax() + k
 +
                if self.A[maxindex, k] == 0:
 +
                    raise ValueError("Matrix is singular.")
 +
                # Swap
 +
                if maxindex != k:
 +
                    self.A[[k, maxindex]] = self.A[[maxindex, k]]
 +
                    self.b[[k, maxindex]] = self.b[[maxindex, k]]
 +
            else:
 +
                if self.A[k, k] == 0:
 +
                    raise ValueError("Pivot element is zero. Try setting doPricing to True.")
 +
            # Eliminate
 +
            for row in range(k + 1, self.n):
 +
                multiplier = self.A[row, k] / self.A[k, k]
 +
                self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
 +
                self.b[row] = self.b[row] - multiplier * self.b[k]
 +
    def _backsub(self):
 +
        # Back Substitution
 +
        self.x = np.zeros(self.n)
 +
        for k in range(self.n - 1, -1, -1):
 +
            self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
 +
def main():
 +
    A = np.array([[6., -4., 0., 0.],
 +
                  [-4., 0., 4., 0.],
 +
                  [-2., 0., -1., 4.],
 +
                  [0., 7., -3., -4.]])
 +
    b = np.array([[50.],
 +
                  [0.],
 +
                  [50.],
 +
                  [0.]])
 +
    print("ini matriks awal nya")
 +
    print(A)
 +
    print("ini hasil yang awal")
 +
    print(b)
 +
    GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
 +
    print("ini hasil akhirnya")
 +
    print(GaussElimPiv.x)
 +
    print(GaussElimPiv.A)
 +
    print(GaussElimPiv.b)
 +
    GaussElimPiv = GEPP(A, b)
 +
    print(GaussElimPiv.x)
 +
if __name__ == "__main__":
 +
    main()
 +
 +
</div>
  
 
<comments voting="Plus" />
 
<comments voting="Plus" />

Revision as of 14:14, 30 September 2019

Pada tugas hiburan ini

S 18382858.jpg

dikerjakan menggunakan hukum kontinuitas massa dimana masa yang masuk akan sama dengan yang dikeluarkan sehingga didapati rumus Q*p=Q*p sehingga akan mendapatakan 4 persamaan dengan 4 variabel


6C1 - 4C2 = 50

-2C1 - 1C3 + 4C4 = 50

7C2 - 3C3 - 4C4 = 0

-4C1 + 4C3 = 0



6C1 - 4C2 + 0C3 + 0C4 = 50

-2C1 + 0C2 - 1C3 + 4C4 = 50

0C1 + 7C2 - 3C3 - 4C4 = 0

-4C1 + 0C2 + 4C3 + 0C4 = 0

yang kemudian dijadikan dalam modue python lalu didapatkan nilai C1 = 275/9 , C2 = 100/3 , C3 = 275/9, C4 = 425/12 


import numpy as np
class GEPP():
   def __init__(self, A, b, doPricing=True):
       #super(GEPP, self).__init__()
       self.A = A                      # input: A is an n x n numpy matrix
       self.b = b                      # b is an n x 1 numpy array
       self.doPricing = doPricing
       self.n = None                   # n is the length of A
       self.x = None                   # x is the solution of Ax=b
       self._validate_input()          # method that validates input
       self._elimination()             # method that conducts elimination
       self._backsub()                 # method that conducts back-substitution
   def _validate_input(self):
       self.n = len(self.A)
       if self.b.size != self.n:
           raise ValueError("Invalid argument: incompatible sizes between" +
                            "A & b.", self.b.size, self.n)
   def _elimination(self):
       """
       k represents the current pivot row. Since GE traverses the matrix in the
       upper right triangle, we also use k for indicating the k-th diagonal
       column index.
       :return
       """
       # Elimination
       for k in range(self.n - 1):
           if self.doPricing:
               # Pivot
               maxindex = abs(self.A[k:, k]).argmax() + k
               if self.A[maxindex, k] == 0:
                   raise ValueError("Matrix is singular.")
               # Swap
               if maxindex != k:
                   self.Ak, maxindex = self.Amaxindex, k
                   self.bk, maxindex = self.bmaxindex, k
           else:
               if self.A[k, k] == 0:
                   raise ValueError("Pivot element is zero. Try setting doPricing to True.")
           # Eliminate
           for row in range(k + 1, self.n):
               multiplier = self.A[row, k] / self.A[k, k]
               self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
               self.b[row] = self.b[row] - multiplier * self.b[k]
   def _backsub(self):
       # Back Substitution
       self.x = np.zeros(self.n)
       for k in range(self.n - 1, -1, -1):
           self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
   A = np.array([[6., -4., 0., 0.],
                 [-4., 0., 4., 0.],
                 [-2., 0., -1., 4.],
                 [0., 7., -3., -4.]])
   b = np.array([[50.],
                 [0.],
                 [50.],
                 [0.]])
   print("ini matriks awal nya")
   print(A)
   print("ini hasil yang awal")
   print(b)
   GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
   print("ini hasil akhirnya")
   print(GaussElimPiv.x)
   print(GaussElimPiv.A)
   print(GaussElimPiv.b)
   GaussElimPiv = GEPP(A, b)
   print(GaussElimPiv.x)
if __name__ == "__main__":
   main()


Edosyafei

62 months ago
Score 0+
Ingin sedikit berkomenta mengenai penyelesaian tugas mengenai kestimbagan 4 tangki konsentrasi. Untuk usaha mencari cara menyelesaikan penyelesaian persamaan aljabar di internet sudah baik. Namun, alangkah lebih baiknya jika saudara menyelesaikannya dengan mengimplentasikan langsung konsep penyelesaian aljabar dengan membuat sendiri algoritma dan kode nya.Diharapkan hal tersebut dapat menambah kemampuan saudara dalam memahami metode numerik dengan menggunakan bantuan komputer

Permalink | Reply

IlliyyinLafi

62 months ago
Score 0+

Berikut kodingan yang saya kerjakan

http://air.e...ran_02-_LAFI

Permalink | Reply

Bagus fadhlurrohman

62 months ago
Score 0+

di bawah ini merupakan hasil tugas saya

http://air.e...an#Hiburan_3

Permalink | Reply

IlliyyinLafi

62 months ago
Score 0+

tugas bagus

Bagus_Fadhlurrohman#Hiburan_3

Permalink | Reply

Anggitoz

62 months ago
Score 0+

Tugas M. Anggito Zhafranny/1706027761

Muhammad_Anggito_Zhafranny#4th_Session

Permalink | Reply

Renoandib

62 months ago
Score 0+

Tugas Ananda Reno Andi Bahar/1706024860

Ananda_Reno_Andi_Bahar#HIBURAN_III

Permalink | Reply

Add your comment
ccitonlinewiki welcomes all comments. If you do not want to be anonymous, register or log in. It is free.

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Metode_Numerik_soal_21_-_Jaringan_pipa&oldid=12321"