Difference between revisions of "Faiz Gading Rahmadana"
| Line 40: | Line 40: | ||
Bila dibandingkan dari ketiga turunan tersebut. Untuk nilai h yang sama. Turunan pusat adalah yang paling akurat. Terima kasih untuk ilmunya hari ini Pak. | Bila dibandingkan dari ketiga turunan tersebut. Untuk nilai h yang sama. Turunan pusat adalah yang paling akurat. Terima kasih untuk ilmunya hari ini Pak. | ||
| + | |||
| + | == '''Pertemuan 4, 24 September 2019''' == | ||
| + | Pertemuan kali ini tidak kalah bermanfaatnya bila dibandingkan dengan pertemuan sebelumnya. Membahas '''Secant, Bisect, dan Newton-Raphson Method'''. Biasa digunakan dalam pencarian pembuat nol dari sebuah fungsi atau dapat disebut root-finding algorithm. Untuk ketiga metode tersebut, Pak Engkos menjelaskan pengertian masing-masing metode. Secant method menggunakan secant lines untukmengaproksimasikan nilai sebuah fungsi. Bila dibandingkan dengan Newton-Raphson, metode ini cukup mirip dengan secant method, namun yang membedakanialah menggunakan finite-difference. Sedangkan untuk bisect method, metode ini untuk mencari akar-akar untuk fungsi yang kontinu dimana diketahui nilai x pada f(x) bernilai positif dan f(x) bernilai negatif. Terima kasih untuk ilmunya hari ini Pak. | ||
| + | |||
| + | == '''Pertemuan 5, 1 Oktober 2019''' == | ||
| + | Pada pertemuan sebelumnya, Pak Engkos telah membahas tiga metode numerik yaitu secant, bisect, dan newton-raphson method. Kali ini beliau membahas '''Truncation Error''' karena semua metode numerik memilikinya. Begitu pula pada kebanyakan software. Meshing adalah hal yang lumrah dilakukan untuk memperkecil truncation error. Meshing sendiri adalah pembagian daerah yang dianalisis menjadi partisi-partisi yang sangat kecil menghasilkan hasil yang akurat. Namun, hasil yang dihasilkan tetap diskrit, meskipun terlihat kontinum jika partisinya sangat kecil. Yang perlu diperhatikan adalah saat partisi terlalu kecil yang berarti pengoperasian perhitungan akan semakin banyak untuk menghasilkan yang akurat. Namun, hal ini berarti rounding akan semakin banyak dan errornya pun semakin besar. Sehingga, untuk menentukan sebesar apa partisinya, terdapat nilai optimum. Untuk mengetahuinya, dapat divariasikan nilai iterasi dari yang kecil hingga besar dan saat tidak memiliki perubahan signifikan maka di titik tersebut ialah jumlah iterasi paling optimum. Terima kasih untuk ilmunya hari ini Pak. | ||
Revision as of 12:58, 20 October 2019
Contents
Profil
Perkenalkan, saya Faiz Gading Rahmadana. Kalian bisa panggil saya Faiz. Jurusan Teknik Mesin. Sekarang tahun ketiga saya. NPM bila kalian butuh, 1706986353. Laman ini akan dipenuhi celotehan saya. Tentu bermanfaat. Terima kasih kepada Dr. Ir. Ahmad Indra Siswantara dan Dr. Ir. Engkos Achmad Kosasih M.T. telah menyediakan tool yang menarik. Bagus untuk mulai nge-blog.
Pertemuan 1, 3 September 2019
Kelas Metode Numerik kali ini cukup menarik perhatian. Sama sekali tidak ada hal lain yang saya lakukan selain memperhatikan ilmu yang diberikan oleh para Dosen. Bagi yang awam istilah Metode Numerik (Metnum). Manusia punya batasan. Butuh bantuan menyelesaikan persoalan matematika. Untuk persoalan dasar saya yakin semuanya hebat. Apalagi Mahasiswa DTM. Dibimbing oleh Dosen-Dosen profesional. Tidak ada keraguan lagi. Nah, Metnum disini adalah teknik yang memformulasikan persoalan matematika hingga bisa dipecahkan dengan perhitungan biasa. Seperti perkalian dan pengurangan. Jadi sangat mempermudah manusia.
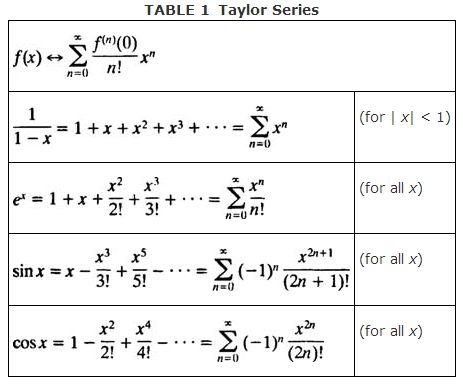
Taylor's Method itu salah satunya. Representasi fungsi matematika intinya. Sebagai jumlahan tak hingga dari suku-suku yang nilainya dihitung dari turunan fungsi tersebut.
Pada kelas kali ini, Pak Engkos meminta Mahasiswa mengaproksimasikan nilai dari Sin(pi/7). Menggunakan rumus umum diatas. Pola didapat yaitu -x^2/2n(2n+1). Masukkan ke dalam Microsoft Excel. Simsalabim. Jawaban pun dapat dicari serinci mungkin. Kesimpulan blog saya kali ini. Hidup ini mudah. Sebetulnya. Hanya perlu perbanyak membaca. Jadi paham bagaimana cara menggunakannya. Ilmu dasar, terutama teknologi. Because, that's why it does exist. Makes everything easier. Terima kasih untuk ilmunya hari ini Pak.
Pertemuan 2, 10 September 2019
Jangan sia-siakan waktu satu detik pun. Tidak ada yang tahu kapan rejeki datang. Mungkin di detik tersebut. Seperti Pandji Pragiwaksono. Saat masih menjadi penyiar Hard Rock FM Bandung. Begitu tertanam pengalaman Pandji di hidup saya. Hari ini pun saya mendapat ilmu penting. Bahasa pemrograman. Sangat banyak manfaatnya. Terutama bidang engineering. Apalagi di jaman sekarang. Serba digital. Pseudo Code dan Bahasa C adalah beberapa contohnya. Pseudo Code adalah algortima dari sebuah pemrogaman komputer menggunakan struktur sederhana dari beberapa bahasa pemrograman yang dapat dibaca manusia. Algoritma ini dijelaskan menggunakan kata-kata. Seperti contoh berikut
Sedangkan Bahasa C adalah bahasa pemrograman yang ditekankan Pak Engkos untuk dipelajari Mahasiswa. Ada beberapa tipe. Float dan Integer merupakan tipe data dasar. Untuk tipe data turunan terdapat Array. Float adalah tipe data untuk menampung angka pecahan. Integer, berfungsi sebagai tipe data yang menampung angka bulat. Array, tipe data yang terdiri dari kumpulan tipe data dasar yang sejenis. Terima kasih untuk ilmunya hari ini Pak.
Pertemuan 3, 17 September 2019
Bila ingin cepat sukses, duduklah di pundak raksasa. Kalimat ini sering terngiang di kepala saya. Dr. Ir. Engkos Achmad Kosasih M.T.. Bagi saya, Beliau masuk kategori raksasa yang dapat membantu saya mendapatkan gelar S.T. dengan tepat. Beliau tidak hanya menjelaskan materi. Namun memberikan alasan. Mengapa harus dengan cara ini. Mengapa tidak menggunakan Phyton. Konsep mengajar seperti ini akan sangat membantu mahasiswa dalam meningkatkan ketertarikannya untuk belajar. Masuk ke materi. Persoalan Turunan Numerik yaitu menentukan nilai hampiran nilai turunan fungsi f. Terdapat tiga pendekatan dalam menentukan turunan numerik. Hampiran selisih maju, hampiran selisih mundur, dan hampiran selisih pusat. Berikut uraiannya.
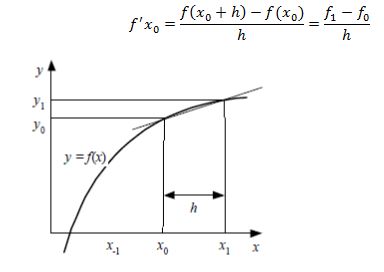
1. Hampiran Selisih Maju (Forward Difference Approximation)
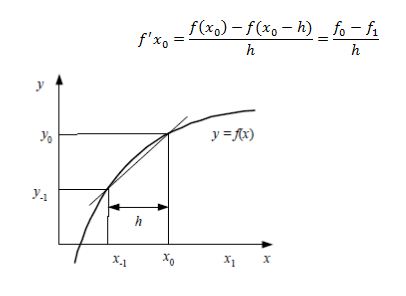
2. Hampiran Selisih Mundur (Backward Difference Approximation)
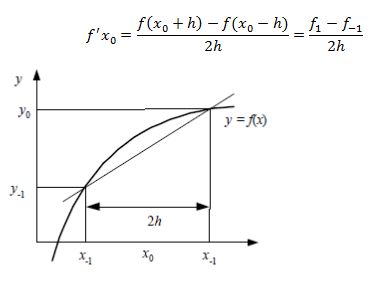
3. Hampiran Selisih Pusat (Central Difference Approximation)
Bila dibandingkan dari ketiga turunan tersebut. Untuk nilai h yang sama. Turunan pusat adalah yang paling akurat. Terima kasih untuk ilmunya hari ini Pak.
Pertemuan 4, 24 September 2019
Pertemuan kali ini tidak kalah bermanfaatnya bila dibandingkan dengan pertemuan sebelumnya. Membahas Secant, Bisect, dan Newton-Raphson Method. Biasa digunakan dalam pencarian pembuat nol dari sebuah fungsi atau dapat disebut root-finding algorithm. Untuk ketiga metode tersebut, Pak Engkos menjelaskan pengertian masing-masing metode. Secant method menggunakan secant lines untukmengaproksimasikan nilai sebuah fungsi. Bila dibandingkan dengan Newton-Raphson, metode ini cukup mirip dengan secant method, namun yang membedakanialah menggunakan finite-difference. Sedangkan untuk bisect method, metode ini untuk mencari akar-akar untuk fungsi yang kontinu dimana diketahui nilai x pada f(x) bernilai positif dan f(x) bernilai negatif. Terima kasih untuk ilmunya hari ini Pak.
Pertemuan 5, 1 Oktober 2019
Pada pertemuan sebelumnya, Pak Engkos telah membahas tiga metode numerik yaitu secant, bisect, dan newton-raphson method. Kali ini beliau membahas Truncation Error karena semua metode numerik memilikinya. Begitu pula pada kebanyakan software. Meshing adalah hal yang lumrah dilakukan untuk memperkecil truncation error. Meshing sendiri adalah pembagian daerah yang dianalisis menjadi partisi-partisi yang sangat kecil menghasilkan hasil yang akurat. Namun, hasil yang dihasilkan tetap diskrit, meskipun terlihat kontinum jika partisinya sangat kecil. Yang perlu diperhatikan adalah saat partisi terlalu kecil yang berarti pengoperasian perhitungan akan semakin banyak untuk menghasilkan yang akurat. Namun, hal ini berarti rounding akan semakin banyak dan errornya pun semakin besar. Sehingga, untuk menentukan sebesar apa partisinya, terdapat nilai optimum. Untuk mengetahuinya, dapat divariasikan nilai iterasi dari yang kecil hingga besar dan saat tidak memiliki perubahan signifikan maka di titik tersebut ialah jumlah iterasi paling optimum. Terima kasih untuk ilmunya hari ini Pak.