Difference between revisions of "Faizal Abizar"
| (30 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File:Screenshot (102).png|thumb| | + | [[File:Screenshot (102).png|thumb|600px|left]] |
Nama : Faizal Abizar | Nama : Faizal Abizar | ||
| Line 7: | Line 7: | ||
Program : S1 Teknik Mesin Paralel | Program : S1 Teknik Mesin Paralel | ||
| − | |||
__FORCETOC__ | __FORCETOC__ | ||
== '''Metode Numerik''' == | == '''Metode Numerik''' == | ||
| + | |||
| + | === '''Pengantar, 2 September 2019''' === | ||
Metode Numerik adalah teknik untuk menyelesaikan permasalahan-permasalahan yang diformulasikan secara matematik dengan cara operasi hitungan (arithmetic). Metode Numerik menurut beberapa ahli : | Metode Numerik adalah teknik untuk menyelesaikan permasalahan-permasalahan yang diformulasikan secara matematik dengan cara operasi hitungan (arithmetic). Metode Numerik menurut beberapa ahli : | ||
| Line 29: | Line 30: | ||
*Solusi selalu berbentuk angka. | *Solusi selalu berbentuk angka. | ||
*Solusi yang dihasilkan adalah solusi pendekatan/hampiran (approxomation), solusi hampiran tidak sama dengan solusi sejati, sehingga ada selisih antara keduanya yang disebut galat atau error. | *Solusi yang dihasilkan adalah solusi pendekatan/hampiran (approxomation), solusi hampiran tidak sama dengan solusi sejati, sehingga ada selisih antara keduanya yang disebut galat atau error. | ||
| + | |||
| + | |||
| + | === '''Pertemuan 2, 9 September 2019''' === | ||
| + | |||
| + | Apakah didunia ini terdapat angka eksak? jawabannya adalah "YA", angka eksak terdiri dari dua angka yaitu angka 0 dan angka 1. Kenapa bisa begitu? karena pada dasarnya angka 0 adalah suatu bilangan yang tidak memiliki nilai dan angka 1 adalah bilangan yang hanya memiliki satu nilai yaitu bernilai 1, dari situ kemudian berkembang angka-angka lain seperti angka 2, angka 3, angka 4, dst. Hal itu didasari ketika contohnya angka 5 yang memiliki nilai 5 adalah kombinasi dari angka satu yang dijumlah sebanyak lima kali (1+1+1+1+1=5). Begitu pula dengan sistem pada komputer yang hanya mengenal 2 angka pada pulse peng-operasiannya. | ||
| + | |||
| + | Pada sistem komputer kita mengenal dengan istilah Bit atau kepanjangan dari “Binary Digit”, yang berarti digit biner. Binary digit adalah unit satuan terkecil dalam komputasi digital. Komputer tidak menggunakan angka desimal untuk menyimpan data. Semua data komputer disimpan dalam angka-angka biner. Hanya 2 nilai berbeda yang bisa dinyatakan satu bit, entah nilai 0 atau nilai 1. Sejarah menyebutkan Istilah “binary digit” atau “bit” diperkenalkan oleh John Tukey di tahun 1947, dimana saat itu ia bekerja sebagai seorang ilmuwan di Bell Laboratories. Sejak saat itu istilah ‘bit’ terus digunakan di dunia komputer. | ||
| + | |||
| + | Dalam sistem komputasi, dikenal istilah Byte yang artinya adalah kumpulan dari beberapa Bit. 1 Byte = 8 Bit. Komputer hanya dapat membaca bilangan Biner dikarenakan pada sistem CPU dan komponen komputer lainnya, memiliki standard command yaitu 0=No / False dan 1=Yes / True. Hal tersebut didasari karena komputer layaknya otak manusia, berkomunikasi dari satu kapasitor dengan kapasitor lainnya menggunakan signal yang disebut dengan Pulse (Denyut) layaknya otak manusia. Kemudian pulse tersebut dapat diterjemahkan kedalam suatau Command (Perintah) yang pada akhirnya Command tersebut dabat dibuat String (Alur) yang akan berakhir menjadi sebuah Algoritma atau yang biasa dikenal dengan Computer Logic (Logika Komputer). Pada akhirnya Computer Logic tersebut dapat disusun menjadi sebuah Program yang sedemikian rupa seperti OS Windows, OS Mac, OS Linux, Aplikasi Komputer, Hingga Image Rendendering pada sebuah program Video Game. | ||
| + | |||
| + | Dapat disimpulkan bahwa komputer hanya memahami satu bilangan yaitu Bilangan Biner, dari bilangan tersebut lahir yang disebut sebagai bahasa komputer seperti Phyton, C+, C++, dll. Setiap bahasa pemrograman tersebut memiliki ciri khas masing-masing namun memiliki satu kesamaan yaitu menggunakan Command inti yang sama yang dapat disusun menjadi sebuah Algoritma. | ||
| + | |||
| + | === '''Pertemuan 3, 16 September 2019''' === | ||
| + | |||
| + | *numeric method class is not finished yet | ||
| Line 71: | Line 87: | ||
[[Video Penjelasan BAB 11]] | [[Video Penjelasan BAB 11]] | ||
| + | == '''Kuis Metode Numerik''' == | ||
| + | === '''Halaman 55 No.6''' === | ||
| + | print ('Selamat datang di Program Hitung Kuis 1 Metnum Faizal Abizar - 1706022211') | ||
| + | |||
| + | import numpy as np | ||
| + | class GEPP(): | ||
| + | |||
| + | def __init__(self, A, b, doPricing=True): | ||
| + | #super(GEPP, self).__init__() | ||
| + | |||
| + | self.A = A # input: A is an n x n numpy matrix | ||
| + | self.b = b # b is an n x 1 numpy array | ||
| + | self.doPricing = doPricing | ||
| + | |||
| + | self.n = None # n is the length of A | ||
| + | self.x = None # x is the solution of Ax=b | ||
| + | |||
| + | self._validate_input() # method that validates input | ||
| + | self._elimination() # method that conducts elimination | ||
| + | self._backsub() # method that conducts back-substitution | ||
| + | |||
| + | def _validate_input(self): | ||
| + | self.n = len(self.A) | ||
| + | if self.b.size != self.n: | ||
| + | raise ValueError("Invalid argument: incompatible sizes between" + | ||
| + | "A & b.", self.b.size, self.n) | ||
| + | |||
| + | def _elimination(self): | ||
| + | |||
| + | |||
| + | # Elimination | ||
| + | for k in range(self.n - 1): | ||
| + | if self.doPricing: | ||
| + | # Pivot | ||
| + | maxindex = abs(self.A[k:, k]).argmax() + k | ||
| + | if self.A[maxindex, k] == 0: | ||
| + | raise ValueError("Matrix is singular.") | ||
| + | # Swap | ||
| + | if maxindex != k: | ||
| + | self.A[[k, maxindex]] = self.A[[maxindex, k]] | ||
| + | self.b[[k, maxindex]] = self.b[[maxindex, k]] | ||
| + | else: | ||
| + | if self.A[k, k] == 0: | ||
| + | raise ValueError("Pivot element is zero. Try setting doPricing to True.") | ||
| + | # Eliminate | ||
| + | for row in range(k + 1, self.n): | ||
| + | multiplier = self.A[row, k] / self.A[k, k] | ||
| + | self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:] | ||
| + | self.b[row] = self.b[row] - multiplier * self.b[k] | ||
| + | |||
| + | def _backsub(self): | ||
| + | # Back Substitution | ||
| + | |||
| + | self.x = np.zeros(self.n) | ||
| + | for k in range(self.n - 1, -1, -1): | ||
| + | self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k] | ||
| + | |||
| + | |||
| + | def main(): | ||
| + | A = np.array([[1., 2., 0., -2., 0.], | ||
| + | [0., 1., 0., 2., -1.], | ||
| + | [0., 0., 2., 1., 2.], | ||
| + | [0., 0., 0., -1., 1.], | ||
| + | [0., 1., -1., 1., -1.]]) | ||
| + | b = np.array([[-4.], | ||
| + | [1.], | ||
| + | [1.], | ||
| + | [-2.], | ||
| + | [-1.]]) | ||
| + | GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False) | ||
| + | print(GaussElimPiv.x) | ||
| + | print(GaussElimPiv.A) | ||
| + | print(GaussElimPiv.b) | ||
| + | GaussElimPiv = GEPP(A, b) | ||
| + | print(GaussElimPiv.x) | ||
| + | |||
| + | if __name__ == "__main__": | ||
| + | main() | ||
| + | |||
| + | Hasil dari perhitungan diatas adalah : | ||
| + | [[File:Screenshot (37).png]] | ||
| + | |||
| + | |||
| + | == '''UTS Metode Numerik''' == | ||
| + | |||
| + | === '''Metode Numerik soal A''' === | ||
| + | print ('Selamat Datang Di UTS METNUM 2019 - Faizal Abizar - 1706022211') | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | class GEPP(): | ||
| + | |||
| + | def __init__(self, A, b, doPricing=True): | ||
| + | #super(GEPP, self).__init__() | ||
| + | |||
| + | self.A = A | ||
| + | self.b = b | ||
| + | self.doPricing = doPricing | ||
| + | |||
| + | self.n = None | ||
| + | self.x = None | ||
| + | |||
| + | self._validate_input() | ||
| + | self._elimination() | ||
| + | self._backsub() | ||
| + | def _validate_input(self): | ||
| + | self.n = len(self.A) | ||
| + | if self.b.size != self.n: | ||
| + | raise ValueError("Invalid argument: incompatible sizes between" + | ||
| + | "A & b.", self.b.size, self.n) | ||
| + | |||
| + | def _elimination(self): | ||
| + | # Elimination | ||
| + | for k in range(self.n - 1): | ||
| + | if self.doPricing: | ||
| + | # Pivot | ||
| + | maxindex = abs(self.A[k:, k]).argmax() + k | ||
| + | if self.A[maxindex, k] == 0: | ||
| + | raise ValueError("Matrix is singular.") | ||
| + | # Swap | ||
| + | if maxindex != k: | ||
| + | self.Ak, maxindex = self.Amaxindex, k | ||
| + | self.bk, maxindex = self.bmaxindex, k | ||
| + | else: | ||
| + | if self.A[k, k] == 0: | ||
| + | raise ValueError("Pivot element is zero. Try setting doPricing to True.") | ||
| + | # Eliminate | ||
| + | for row in range(k + 1, self.n): | ||
| + | multiplier = self.A[row, k] / self.A[k, k] | ||
| + | self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:] | ||
| + | self.b[row] = self.b[row] - multiplier * self.b[k] | ||
| + | |||
| + | def _backsub(self): | ||
| + | # Back Substitution | ||
| + | self.x = np.zeros(self.n) | ||
| + | for k in range(self.n - 1, -1, -1): | ||
| + | self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k] | ||
| + | def main(): | ||
| + | A = np.array([[6., -4., 0., 0.], | ||
| + | [-4., 0., 4., 0.], | ||
| + | [-2., 0., -1., 4.], | ||
| + | [0., 7., -3., -4.]]) | ||
| + | b = np.array([[50.], | ||
| + | [0.], | ||
| + | [50.], | ||
| + | [0.]]) | ||
| + | print("Matriks Awal") | ||
| + | print(A) | ||
| + | print("Hasil Matriks Awal") | ||
| + | print(b) | ||
| + | |||
| + | GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False) | ||
| + | print("Hasil Akhir") | ||
| + | print(GaussElimPiv.x) | ||
| + | print(GaussElimPiv.A) | ||
| + | print(GaussElimPiv.b) | ||
| + | GaussElimPiv = GEPP(A, b) | ||
| + | print(GaussElimPiv.x) | ||
| + | if __name__ == "__main__": | ||
| + | main() | ||
| + | |||
| + | Untuk Hasil Perhitungan Saya Lampirkan Sebagai Berikut : | ||
| + | [[File:Screenshot (150).png]] | ||
| + | |||
| + | Berikut saya lampirkan penyelesaian soal A: | ||
| + | <youtube width="200" height="100">YHTIpkPq75s</youtube> | ||
| + | |||
| + | === '''Metode Numerik soal B''' === | ||
| + | 'UTS Metode Numerik 2019, 21 Oktober 2019' | ||
| + | 'Faizal Abizar - 1706022211' | ||
| + | #masukan plugin numpy | ||
| + | import numpy as np | ||
| + | def diff_y (x,y): | ||
| + | fungsi = x**2 - 4*y | ||
| + | return (fungsi) | ||
| + | |||
| + | #definisikan syarat perhitungan | ||
| + | x=0 | ||
| + | y=1 | ||
| + | h=0.5 | ||
| + | step_size = 0.5 | ||
| + | step_size = -np.arange (0,0.5,h) | ||
| + | for t in step_size: | ||
| + | k1 = diff_y (x,y) | ||
| + | k2 = diff_y ((x+0.5*h),(y+0.05*k1*h)) | ||
| + | |||
| + | #simulasi hasil | ||
| + | w1 = y + 1/3*(k1+2*k2) | ||
| + | |||
| + | #cek kecepatan pada saat 0,7 detik | ||
| + | print ('maka x(0.7) sama dengan', w1) | ||
| + | |||
| + | dan didapatkan hasil sebagai berikut: | ||
| + | |||
| + | |||
| + | [[File:Utshariini.png]] | ||
| + | |||
| + | Berikut saya lampirkan video penjelasan penggunaan script soal B: | ||
| + | <youtube width="200" height="100">bUsE-3yaJdc</youtube> | ||
== '''Daftar Tugas''' == | == '''Daftar Tugas''' == | ||
=== '''Metode Numerik''' === | === '''Metode Numerik''' === | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | def f(x): | ||
| + | return 8*x**3 + 2*x**2 + x - 1 | ||
| + | def fprime(x): | ||
| + | return 24*x**2 + 4*x +1 | ||
| + | <br>ep = 0.001 | ||
| + | <br>gu = -10 | ||
| + | i = 0 | ||
| + | <br>print('8*x**3 + 2*x**2 + x - 1') | ||
| + | <br>print('Results by Python 3.7') | ||
| + | <br>while abs(f(gu)) >= ep: | ||
| + | gu = gu - (f(gu)/fprime(gu)) | ||
| + | i += 1 | ||
| + | print(' ' + str(i) + ' ' + str(round(gu,7))) | ||
| + | <br>print('The root approach is ' + str(round(gu,2)) + | ||
| + | '| failed to calculate: ' + str(i) + ' times' ) | ||
| + | </div> | ||
| + | |||
| + | |||
| + | '''Tugas 2''' | ||
| + | |||
| + | Konversi dan Eliminasi menggunakan Gaussian Elimination: | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | 6x<sub>1</sub> + 4x<sub>2</sub> = 50 | ||
| + | 2x<sub>1</sub> + x<sub>3</sub> + 4x<sub>4</sub> = 50 | ||
| + | 7x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> = 50 | ||
| + | 4x<sub>1</sub> + 4x<sub>3</sub> = 50 | ||
| + | |||
| + | Masukan kedalam persamaan matriks: | ||
| + | [[6. 4. 0. 0.] | ||
| + | [2. 0. 1. 4.] | ||
| + | [0. 7. 3. 4.] | ||
| + | [4. 0. 4. 0.]] | ||
| + | </div> | ||
| + | |||
| + | Kemudian masukan matriks kedalam program Phyton: | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | import numpy as np | ||
| + | <br>A = np.array([[6, 4, 0, 0], [2, 0 ,1, 4], [0, 7, 3, 4], [ 4, 0, 4, 0]], float) | ||
| + | B = np.array([50, 50, 0, 0], float) | ||
| + | <br>n = len(A) | ||
| + | </div> | ||
| + | |||
| + | Gunakan Gaussian Elimination | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | for k in range(0,n-1): | ||
| + | for i in range(k+1,n): | ||
| + | if A[i,k]!=0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) | ||
| + | B[i] = B[i]-(B[k]*lam) | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <div border-style: inset;"> | ||
| + | x = np.zeros(n,float) | ||
| + | for m in range(n-1,-1,-1): | ||
| + | x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m] | ||
| + | </div> | ||
| + | '''Results''' | ||
| + | |||
=== '''Mekanika Fluida''' === | === '''Mekanika Fluida''' === | ||
| Line 87: | Line 367: | ||
| + | |||
| + | == '''Muhasabah Diri''' == | ||
| + | <youtube width="200" height="100">pcZMtWVNJiE</youtube> | ||
== '''Referensi''' == | == '''Referensi''' == | ||
MUNSON, B. R., YOUNG, D. F., & OKIISHI, T. H. (2006). Fundamentals of fluid mechanics. Hoboken, NJ, J. Wiley & Sons. | MUNSON, B. R., YOUNG, D. F., & OKIISHI, T. H. (2006). Fundamentals of fluid mechanics. Hoboken, NJ, J. Wiley & Sons. | ||
Latest revision as of 00:02, 28 October 2019
Nama : Faizal Abizar
NPM : 1706022211
Program : S1 Teknik Mesin Paralel
Contents
Metode Numerik
Pengantar, 2 September 2019
Metode Numerik adalah teknik untuk menyelesaikan permasalahan-permasalahan yang diformulasikan secara matematik dengan cara operasi hitungan (arithmetic). Metode Numerik menurut beberapa ahli :
- Chapra dan Chanale
"Metode numerik adalah teknik di mana masalah matematika diformulasikan sedemikian rupa sehingga dapat diselesaikan oleh pengoperasian aritmetika."
- Ibraheem dan Hisyam
"Metode numerik adalah teknik -teknik yang digunakan untuk merumuskan masalah matematika agar dapat diselesaikan hanya dengan operasi hitungan, yang terdiri dari operasi tambah, kurang, kali dan bagi."
- Rochmad
"Metode numerik adalah suatu teknik untuk memformulasikan masalah matematika sehingga dapat diselesaikan dengan operasi aritmetika yang terdiri dari operasi tambah, kurang, kali dan bagi."
Metode Numerik Memiliki Karakteristik Yaitu :
- Solusi selalu berbentuk angka.
- Solusi yang dihasilkan adalah solusi pendekatan/hampiran (approxomation), solusi hampiran tidak sama dengan solusi sejati, sehingga ada selisih antara keduanya yang disebut galat atau error.
Pertemuan 2, 9 September 2019
Apakah didunia ini terdapat angka eksak? jawabannya adalah "YA", angka eksak terdiri dari dua angka yaitu angka 0 dan angka 1. Kenapa bisa begitu? karena pada dasarnya angka 0 adalah suatu bilangan yang tidak memiliki nilai dan angka 1 adalah bilangan yang hanya memiliki satu nilai yaitu bernilai 1, dari situ kemudian berkembang angka-angka lain seperti angka 2, angka 3, angka 4, dst. Hal itu didasari ketika contohnya angka 5 yang memiliki nilai 5 adalah kombinasi dari angka satu yang dijumlah sebanyak lima kali (1+1+1+1+1=5). Begitu pula dengan sistem pada komputer yang hanya mengenal 2 angka pada pulse peng-operasiannya.
Pada sistem komputer kita mengenal dengan istilah Bit atau kepanjangan dari “Binary Digit”, yang berarti digit biner. Binary digit adalah unit satuan terkecil dalam komputasi digital. Komputer tidak menggunakan angka desimal untuk menyimpan data. Semua data komputer disimpan dalam angka-angka biner. Hanya 2 nilai berbeda yang bisa dinyatakan satu bit, entah nilai 0 atau nilai 1. Sejarah menyebutkan Istilah “binary digit” atau “bit” diperkenalkan oleh John Tukey di tahun 1947, dimana saat itu ia bekerja sebagai seorang ilmuwan di Bell Laboratories. Sejak saat itu istilah ‘bit’ terus digunakan di dunia komputer.
Dalam sistem komputasi, dikenal istilah Byte yang artinya adalah kumpulan dari beberapa Bit. 1 Byte = 8 Bit. Komputer hanya dapat membaca bilangan Biner dikarenakan pada sistem CPU dan komponen komputer lainnya, memiliki standard command yaitu 0=No / False dan 1=Yes / True. Hal tersebut didasari karena komputer layaknya otak manusia, berkomunikasi dari satu kapasitor dengan kapasitor lainnya menggunakan signal yang disebut dengan Pulse (Denyut) layaknya otak manusia. Kemudian pulse tersebut dapat diterjemahkan kedalam suatau Command (Perintah) yang pada akhirnya Command tersebut dabat dibuat String (Alur) yang akan berakhir menjadi sebuah Algoritma atau yang biasa dikenal dengan Computer Logic (Logika Komputer). Pada akhirnya Computer Logic tersebut dapat disusun menjadi sebuah Program yang sedemikian rupa seperti OS Windows, OS Mac, OS Linux, Aplikasi Komputer, Hingga Image Rendendering pada sebuah program Video Game.
Dapat disimpulkan bahwa komputer hanya memahami satu bilangan yaitu Bilangan Biner, dari bilangan tersebut lahir yang disebut sebagai bahasa komputer seperti Phyton, C+, C++, dll. Setiap bahasa pemrograman tersebut memiliki ciri khas masing-masing namun memiliki satu kesamaan yaitu menggunakan Command inti yang sama yang dapat disusun menjadi sebuah Algoritma.
Pertemuan 3, 16 September 2019
- numeric method class is not finished yet
Mekanika Fluida
Mekanika Fluida adalah cabang dari ilmu fisika yang mempelajari mengenai zat fluida (cair, gas dan plasma) dan gaya yang bekerja padanya. Mekanika fluida dapat dibagi menjadi statika fluida, ilmu yang mempelajari keadaan fluida saat diam; kinematika fluida, ilmu yang mempelajari fluida yang bergerak; dan dinamika fluida, ilmu yang mempelajari efek gaya pada fluida yang bergerak. Ini adalah cabang dari mekanika kontinum, sebuah subjek yang memodelkan materi tanpa memperhatikan informasi mengenai atom penyusun dari materi tersebut sehingga hal ini lebih berdasarkan pada sudut pandang makroskopik daripada sudut pandang mikroskopik. Mekanika fluida, terutama dinamika fluida, adalah bidang penelitian utama dengan banyak hal yang belum terselesaikan atau hanya sebagian yang terselesaikan. Mekanika fluida dapat menjadi sangat rumit secara matematika, dan sangat tepat untuk diselesaikan dengan metode numerik, biasanya dengan menggunakan perhitungan komputer. Dinamika Fluida Komputasi, adalah salah satu disiplin yang dikhususkan untuk penyelesaian masalah mekanika fluida dengan pendekatan numerik.
BAB 8 : Viskositas Aliran Pipa
Pada BAB ini kita mempelajari tentang bagaimana karakteristik suatu aliran dalam sebuah pipa dan dapat mengamati perbedaan tekanan pada kedua ujung pipa atau biasa disebut dari titik A ke titik B.Berikut saya lampirkan penjelasan saya mengenai BAB 8 ini yang sudah saya rangkum ke dalam sebuah video.
Youtube
BAB 9 : Flow Over Immersed Bodies
Pada BAB ini kita akan mempelajari tentang karakteristik fluida apabila mengalir pada benda yang terbenam atau terendam. Ilmu ini banyak diterapkan didalam kehidupan sehari-hari contohnya adalah dalam mendesign pesawat terbang, helikopter, dkapal selam, dan lain-lain dengan memeprhatikan gaya-gaya yang terjadi pada sekitar (lingkungan) dari objek tersebut.
BAB 10 : Aliran Open-Channel
Jika pada BAB 8 dan BAB 9 kita mempelajari aliran pipa tertutup (Close-Channel), pada BAB ini kita mempelajari sesuatu yang sedikit berbeda yaitu Aliran Open-Channel. Aliran ini berbeda dengan Close-Channel karena pada aliran ini fluida tidak mengalir sepenuhnya pada sebuah pipa atau saluran air. Hal ini dapat kita lihat disekitar kita contohnya adalah saluran air depan rumah (selokan) dan sungai yang tingkat kesulitan dari perhitungannya bisa dibilang cukup rumit mengingat kita harus mengukur dan menentukan spesifikasi dari tempat fluida mengalir tersebut. Kerumitan ditambah juga dengan pebedaan kemiringan pada objek yang menyebabkan tekanan yang mengalir tidak sama pada setiap titik.
BAB 11 : Aliran Compressible
Pada BAB ini kita akan mempelajari tentang fluida mampu mampat, fluida yang compressible adalah fluida yang kerapatannya dapat berubah karena perubahan tekanan dan temperatur. Contoh fluida compressible adalah gas nitrogen dan oksigen.
Kuis Metode Numerik
Halaman 55 No.6
print ('Selamat datang di Program Hitung Kuis 1 Metnum Faizal Abizar - 1706022211')
import numpy as np class GEPP():
def __init__(self, A, b, doPricing=True):
#super(GEPP, self).__init__()
self.A = A # input: A is an n x n numpy matrix
self.b = b # b is an n x 1 numpy array
self.doPricing = doPricing
self.n = None # n is the length of A
self.x = None # x is the solution of Ax=b
self._validate_input() # method that validates input
self._elimination() # method that conducts elimination
self._backsub() # method that conducts back-substitution
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("Invalid argument: incompatible sizes between" +
"A & b.", self.b.size, self.n)
def _elimination(self):
# Elimination
for k in range(self.n - 1):
if self.doPricing:
# Pivot
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
# Swap
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("Pivot element is zero. Try setting doPricing to True.")
# Eliminate
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[1., 2., 0., -2., 0.],
[0., 1., 0., 2., -1.],
[0., 0., 2., 1., 2.],
[0., 0., 0., -1., 1.],
[0., 1., -1., 1., -1.]])
b = np.array([[-4.],
[1.],
[1.],
[-2.],
[-1.]])
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
print(GaussElimPiv.x)
print(GaussElimPiv.A)
print(GaussElimPiv.b)
GaussElimPiv = GEPP(A, b)
print(GaussElimPiv.x)
if __name__ == "__main__":
main()
Hasil dari perhitungan diatas adalah :

UTS Metode Numerik
Metode Numerik soal A
print ('Selamat Datang Di UTS METNUM 2019 - Faizal Abizar - 1706022211')
import numpy as np
class GEPP():
def __init__(self, A, b, doPricing=True):
#super(GEPP, self).__init__()
self.A = A
self.b = b
self.doPricing = doPricing
self.n = None
self.x = None
self._validate_input()
self._elimination()
self._backsub()
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("Invalid argument: incompatible sizes between" +
"A & b.", self.b.size, self.n)
def _elimination(self):
# Elimination
for k in range(self.n - 1):
if self.doPricing:
# Pivot
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
# Swap
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("Pivot element is zero. Try setting doPricing to True.")
# Eliminate
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[6., -4., 0., 0.],
[-4., 0., 4., 0.],
[-2., 0., -1., 4.],
[0., 7., -3., -4.]])
b = np.array([[50.],
[0.],
[50.],
[0.]])
print("Matriks Awal")
print(A)
print("Hasil Matriks Awal")
print(b)
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
print("Hasil Akhir")
print(GaussElimPiv.x)
print(GaussElimPiv.A)
print(GaussElimPiv.b)
GaussElimPiv = GEPP(A, b)
print(GaussElimPiv.x)
if __name__ == "__main__":
main()
Untuk Hasil Perhitungan Saya Lampirkan Sebagai Berikut :
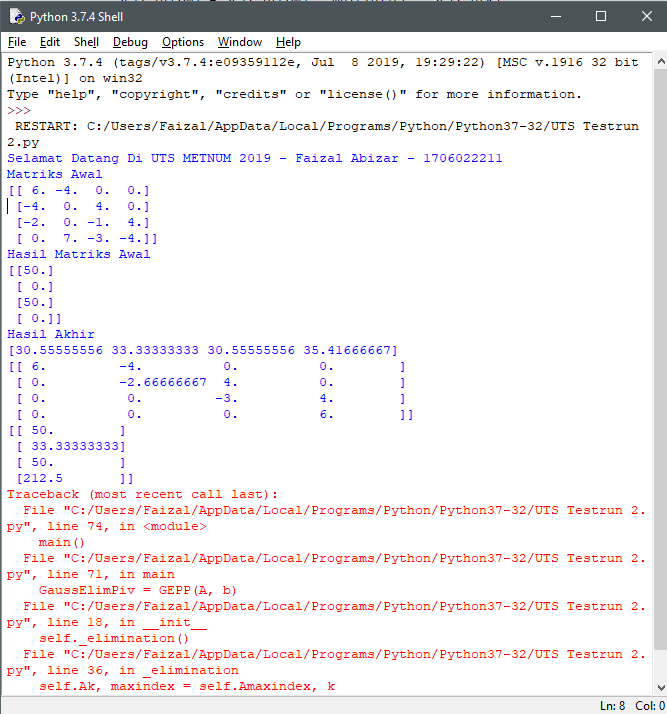
Berikut saya lampirkan penyelesaian soal A:
Metode Numerik soal B
'UTS Metode Numerik 2019, 21 Oktober 2019'
'Faizal Abizar - 1706022211'
#masukan plugin numpy
import numpy as np
def diff_y (x,y):
fungsi = x**2 - 4*y
return (fungsi)
#definisikan syarat perhitungan
x=0
y=1
h=0.5
step_size = 0.5
step_size = -np.arange (0,0.5,h)
for t in step_size:
k1 = diff_y (x,y)
k2 = diff_y ((x+0.5*h),(y+0.05*k1*h))
#simulasi hasil
w1 = y + 1/3*(k1+2*k2)
#cek kecepatan pada saat 0,7 detik
print ('maka x(0.7) sama dengan', w1)
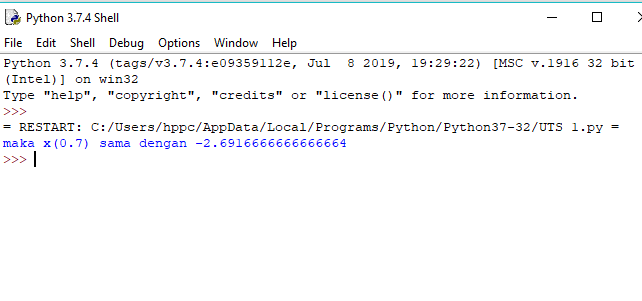
dan didapatkan hasil sebagai berikut:
Berikut saya lampirkan video penjelasan penggunaan script soal B:
Daftar Tugas
Metode Numerik
def f(x): return 8*x**3 + 2*x**2 + x - 1 def fprime(x): return 24*x**2 + 4*x +1
ep = 0.001
gu = -10 i = 0
print('8*x**3 + 2*x**2 + x - 1')
print('Results by Python 3.7')
while abs(f(gu)) >= ep: gu = gu - (f(gu)/fprime(gu)) i += 1 print(' ' + str(i) + ' ' + str(round(gu,7)))
print('The root approach is ' + str(round(gu,2)) + '| failed to calculate: ' + str(i) + ' times' )
Tugas 2
Konversi dan Eliminasi menggunakan Gaussian Elimination:
6x1 + 4x2 = 50 2x1 + x3 + 4x4 = 50 7x2 + 3x3 + 4x4 = 50 4x1 + 4x3 = 50
Masukan kedalam persamaan matriks:
[[6. 4. 0. 0.] [2. 0. 1. 4.] [0. 7. 3. 4.] [4. 0. 4. 0.]]
Kemudian masukan matriks kedalam program Phyton:
import numpy as np
A = np.array([[6, 4, 0, 0], [2, 0 ,1, 4], [0, 7, 3, 4], [ 4, 0, 4, 0]], float) B = np.array([50, 50, 0, 0], float)
n = len(A)
Gunakan Gaussian Elimination
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
Results
Mekanika Fluida
Muhasabah Diri
Referensi
MUNSON, B. R., YOUNG, D. F., & OKIISHI, T. H. (2006). Fundamentals of fluid mechanics. Hoboken, NJ, J. Wiley & Sons.