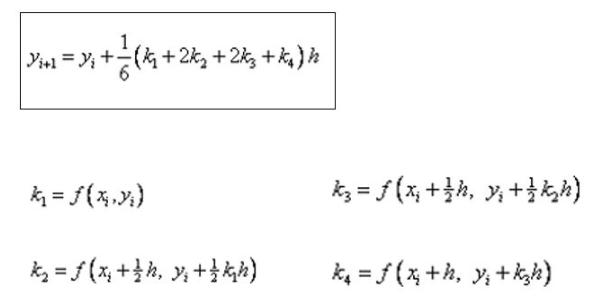Difference between revisions of "Dika Auliady"
Dikaauliady (talk | contribs) |
Dikaauliady (talk | contribs) (→Biodata) |
||
| (46 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | == Profil == | ||
| + | |||
| + | [[File:Foto.PNG]] | ||
| + | |||
| + | Nama : Dika Auliady | ||
| + | |||
| + | NPM : 1706070671 | ||
| + | |||
| + | Jurusan : Teknik Mesin | ||
| + | |||
== Biodata == | == Biodata == | ||
| − | Nama : Dika Auliady | + | Nama Lengkap : Dika Auliady |
| + | |||
| + | Tempat tanggal lahir : Jakarta | ||
| + | |||
| + | Alamat : BSD | ||
| + | |||
| + | == Metode Numerik == | ||
| + | |||
| + | ''Pertemuan 1 : 2 September 2019'' | ||
| + | -------- | ||
| + | |||
| + | Pada pertemuan pertama ini membahas tentang apa itu metode numerik. Metode numerik adalah mata kuliah yang mempelajari tentang bahasa pemrograman untuk bisa menyelesaikan sebuah persoalan dengan cara numerik bukan secara analitik. Karena pada kehidupan sehari-hari baik di teknik maupun bukan banyak permasalahan yang tidak bisa diselesaikan secara analitik. Contohnya untuk menyelesaikan sebuah persamaan di pegas dapat diselesaikan dengan mudah secara analitik namun, apabila pegas yang digunakan lebih banyak tentu menyelesaikannya akan lebih lama dan lebih sulit. Jadi untuk mengatasi ini, ada beberapa bahasa pemrograman sepeti python,matlab,C++, dan lain-lain untuk bisa menerjemahkan dari manusia ke komputer. | ||
| + | |||
| + | Phyton merupakan salah satu dari berbagai bahasa pemrograman yang berguna untuk mengkomunikasikan antara user dengan komputer. Dalam metode numerik bisa digunakan untuk menyelesaikan persoalan matematika yang rumit menjadi lebih mudah dan lebih cepat. | ||
| + | |||
| + | Mode interaktif merupakan fasilitas/fitur yang disediakan oleh Python sebagai tempat menulis kode secara interaktif. Fitur ini dikenal juga dengan Shell, Console, REPL (Read–Eval–Print Loop), interpreter, dsb. Cara membuka mode interaktif adalah dengan mengetik perintah python pada terminal. | ||
| + | |||
| + | Tanda >>>, artinya python siap menerima perintah. Terdapat juga tanda ... yang berarti secondary prompt atau sub prompt, biasanya muncul saat membuat blok kode dan menulis perintah tunggal dalam beberapa baris.perintah print, perintah ini berfungsi untuk mencetak teks ke layar. | ||
| + | |||
| + | Dari hasil diskusi pada pertemuan ini, bilangan eksak adalah bilangan yang pasti seperti 0,1,2 dan seterusnya merupakan | ||
| + | 1. Hanya kesepakatan untuk mempermudah perhitungan dalam kehidupan | ||
| + | 2. Merupakan pendekatan untuk menyelesaikan persoalan karena ada beberapa masalah yang tidak memiliki hasil atau tidak dapat terdefinisi hasilnya | ||
| + | Jadi sebenarnya bilangan eksak itu tidak ada, dan menurut bahasanya eksak artinya adalah pasti maka sebenar-benarnya yang pasti hanyalah tuhan kita Allah saja. | ||
| + | |||
| + | |||
| + | ''Pertemuan 2 : 9 September 2019'' | ||
| + | ----------- | ||
| + | |||
| + | Melanjutkan dari bahasan sebelumnya untuk mencari nilai dari hasil sebuah penyelesaian pada python perlu beberapa step dan tidak bisa langsung menggunakan satu perintah dan menemukan hasilnya, perlu menggunakan trial and error jadi alur pengerjaan pada python ini ada 3, yaitu algoritma,flowchart,code python. | ||
| + | Untuk lebih jelasnya ada contoh soal yang diberikan seperti dibawah | ||
| + | |||
| + | def limit(x) : | ||
| + | try: | ||
| + | a = (x**2-1) | ||
| + | b = (x-1) | ||
| + | result = a/b | ||
| + | print (result) | ||
| + | except ZeroDivisonError : | ||
| + | c = ((x+(1/99))**2-1) / ((x+(1/99))-1) | ||
| + | print (c) | ||
| + | d = ((x+(1/999))**2-1) / ((x+(1/999))-1) | ||
| + | print (d) | ||
| + | e = ((x+(1/9999))**2-1) / ((x+(1/9999))-1) | ||
| + | print (e) | ||
| + | f = ((x+(1/99999))**2-1) / ((x+(1/99999))-1) | ||
| + | print (f) | ||
| + | g = ((x+(1/999999))**2-1) / ((x+(1/999999))-1) | ||
| + | print (g) | ||
| + | h = ((x+(1/9999999))**2-1) / ((x+(1/9999999))-1) | ||
| + | print (h) | ||
| + | |||
| + | [[Soal 1]] | ||
| + | |||
| + | [[Soal 2]] | ||
| + | |||
| + | Dari soal-soal limit ini tujuannya sama yaitu melakukan pendekatan untuk menemukan jawaban yang pasti dengan metode limit. | ||
| + | pada persamaan pertama kita mau mendapatkan hasil terdefinisi maka untuk itu nilai x tidak boleh satu tetapi harus mendekati satu. | ||
| + | Hasilnya dari 6 kali percobaan adalah mendekati angka 2. | ||
| + | Kenapa menggunakan zerodivisonerror adalah agar untuk tidak terjadi eror angka 0. | ||
| + | Cara pengerjaannya seperti biasa, pertama kita harus menjelaskan apa itu fungsi x lalu | ||
| + | masukan perintah zerodivision eror dan print hasilnya. | ||
| + | |||
| + | |||
| + | ''Pertemuan 3 : 16 September 2019'' | ||
| + | ------ | ||
| + | |||
| + | #define fungsi T | ||
| + | def fungsi_T(x): | ||
| + | T = (x**2-1)/(x-1) | ||
| + | return (T) | ||
| + | |||
| + | #2 assign x = 0, delta_x = 0.1 | ||
| + | x = 0 | ||
| + | delta_x = 0.1 | ||
| + | error = 1 | ||
| + | |||
| + | To = fungsi_T(x) | ||
| + | |||
| + | print ('x adalah', x) | ||
| + | |||
| + | print ('Nilai T awal adalah', To) | ||
| + | |||
| + | x = x+delta_x | ||
| + | |||
| + | Tn = fungsi_T(x) | ||
| + | |||
| + | error = abs ((To-Tn/To)) | ||
| + | |||
| + | print ('Nilai T selanjutnya', Tn) | ||
| + | |||
| + | print ('Error nya adalah', error) | ||
| + | |||
| + | x = x+delta_x | ||
| + | |||
| + | To = Tn | ||
| + | |||
| + | Tn = fungsi_T(x) | ||
| + | |||
| + | error = abs ((To-Tn/To)) | ||
| + | |||
| + | print ('Nilai T selanjutnya', Tn) | ||
| + | |||
| + | print ('Error nya adalah', error) | ||
| + | |||
| + | |||
| + | Dalam menyelesaikan sebuah fungsi limit banyak cara yang bisa dilakukan. Pada pertemuan kali ini mempelajari tentang loop | ||
| + | yaitu apabila kita menginginkan sebuah hasil tetapi dengan syarat suatu kondisi maka cara dapat diterapkan. | ||
| + | Jadi dengan menggunakan soal di pertemuan sebelumnya, kita dapat menentukan syarat seperti apabila x nya masih kurang dari 1 maka perintah ini akan terus berjalan menyelesaikan persamaan atau dengan menggunakan errornya, karena error akan terus menuju 0. Untuk Tn adalah perbaharuan To atau T awal sementara delta_x adalah pertambahan yang kita inginkan untuk menuju ke 1 dimulai dari 0. Error adalah perbandingan selisih hasil fungsi yang baru dan yang lama. | ||
| + | |||
| + | |||
| + | ''Pertemuan 4 : 23 September 2019'' | ||
| + | ------ | ||
| + | |||
| + | Pada pertemuan kali membahas tentang aplikasi pyhton pada sebuah sistem pipa. Sebelum itu kita harus mengetahui bentuk matematis dari soal yang dimaksud yaitu pada kasus ini dalam bentuk sebuah matriks. Penyelesaian matriks pada python dapat dikerjakan dengan eliminasi gauss. Berikut adalah langkah penyelesaiannya | ||
| + | |||
| + | [[File:Pipapipa.jpg]] | ||
| + | |||
| + | Pertama mencari persamaan | ||
| + | |||
| + | 6c1 - 4c2 = 50 | ||
| + | |||
| + | -2c1 - c3 + 4c4 = 50 | ||
| + | |||
| + | 7c2 - 3c3 - 4c4 = 50 | ||
| + | |||
| + | -4c1 + 4c3 = 50 | ||
| + | |||
| + | |||
| + | |||
| + | Dalam bentuk matriks | ||
| + | |||
| + | [6. -4. 0. 0.] | ||
| + | |||
| + | [-4. 0. 4. 0.] | ||
| + | |||
| + | [-2. 0. -1. 4.] | ||
| + | |||
| + | [0. 7. -3. -4.] | ||
| + | |||
| + | |||
| + | |||
| + | Lalu masukan ke dalam code python | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | A = np.array([[6,-4,0,0], [-4,0,4,0], [-2,0,-1,4], [0,7,-3,-4]], float) | ||
| + | |||
| + | B = np.array([50,0,50,0], float) | ||
| + | print ('Matriks A adalah', A) | ||
| + | print ('Matriks B adalah', B) | ||
| + | n = len (A) | ||
| + | |||
| + | for k in range(0,n-1): | ||
| + | for i in range(k+1,n): | ||
| + | if A[i,k]!=0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) | ||
| + | B[i] = B[i]-(B[k]*lam) | ||
| + | print ('Matriks A setelah eliminasi Gauss :', '\n', A) | ||
| + | |||
| + | x = np.zeros(n, float) | ||
| + | |||
| + | for m in range(n-1,-1,-1): | ||
| + | x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m] | ||
| + | print ('Nilai X', m+1, '=', x[m]) | ||
| + | |||
| + | Perintah untuk menerapkan numpy dalam coding ini agar mempermudah berbagai bentuk matematik digunakan dalam coding ini. Array berguna untuk membuat data yang dinginkan dituliskan dalam format matrix.Baris 2 dan 3 memunculkan matrix. Matrix yang muncul adalah matrix A dan B karena perintah print ditujukan kepada keduanya. Baris 4 dan 5 perintah menuliskan apa yang ada di dalamnya. Baris 6 mengetahui ukuran matriks dari A. Dalam kasus ini, nilai tersebut adalah 4x4. Float tidak termasuk jenis data lain karena itu berguna untuk mendefinisikan nilai desimal. Baris 7 -12 proses eliminasi bagian dari baris yang harusnya 0. Karena kita memerlukan matrix segitiga bawah untuk menyelesaikan dengan metode elimination gauss. For digunakan untuk menjalankan perintah hanya ketika argumen yang ada bersifat true. Proses yang berjalan adalah pengecekan setiap angka pada segitiga bawah dalam matrix tersebut agar nilainya menjadi 0. Baris 8 perintah for yang berarti hanya berjalan kalau argumennya bersifat true. Range disini berarti dimana kita akan memulai pivot. If digunakan untuk apabila nilai pada matriks sudah bernilai 0 maka diperlu lagi dilakukan pengoperasian. Lam merupakan pembagian nilai di koordinat data yang diberikan, setelah membentuk segitiga bawah nilai x dapat ditentukan. tetapi ada penggunaan np.dot disana. Baris 14 zero matrix yang berarti x adalah sebuah matrik yang kosong. Selanjutnya ada back subtitution. Perintah np.dot sama seperti dot product dalam aljabar linear. Baris terakhir print (x[m]). | ||
| + | Selesai. | ||
| + | |||
| + | [[Hiburan 3]] | ||
| + | |||
| + | |||
| + | ''Pertemuan 6 : 7 Oktober 2019'' | ||
| + | -------- | ||
| + | |||
| + | Di pertemuan ini mempelajari tentang Runge-Kutta 4th order yaitu sebuah pendekatan dari sebuah grafik dengan menggunakan turunan keempat. | ||
| + | Lebih jelasnya diajarkan dalam bentuk soal | ||
| + | |||
| + | Sebuah bola jatuh dengan kecepatan awal 0 pada jarak 100 m, hanya dipengaruhi percepatan gravitasi sebesar 10 m/s2 | ||
| + | tentukan kecepatan dan tinggi bola setelah 4 detik | ||
| + | |||
| + | Pada pertemuan kali ini belum menggunakan python tetapi dengan excel agar pemahamannya lebih mudah. | ||
| + | Yang pertama kali harus dilakukan adalah menentukan turunan pertama dari fungsi kecepatan dan fungsi posisi nya atau dv/dt dan dy/dt. | ||
| + | Setelah mengetahui dv/dt = -g dan dy/dt = -gt maka hanya dengan memasukannya ke dalam rumus bisa didapatkaklah hasilnya. | ||
| + | |||
| + | [[File:Qwe.PNG]] | ||
| + | |||
| + | [[File:Mbnv.PNG]] | ||
| + | |||
| + | Dengan h sebesar 0,2 artinya kita mencari data setiap 0,2 detik setelahnya sampai akhirnya di 4 detik karena ini merupakan pendekatan yang tidak bisa langsung mendapat hasilnya. | ||
| + | |||
| + | |||
| + | ''Pertemuan 7 : 14 Oktober 2019'' | ||
| + | ------- | ||
| + | |||
| + | Kuis metode numerik | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | #1. definisi matriks | ||
| + | A = np.array ([[1,2,0,-2,0], [0,1,0,2,-1], [0,0,2,1,2], [0,0,0,-1,1], [0,1,-1,1,-1]], float) | ||
| + | B = np.array ([1,1,-4,-2,-1], float) | ||
| + | |||
| + | n = len(A) | ||
| + | |||
| + | #2. eliminasi gauss | ||
| + | |||
| + | for k in range (0,n-1) : #k adalah baris pivot dimulai dari 0 sampai n-1 | ||
| + | for i in range (k+1, n) : #i adalah baris dibawah pivot sampai terakhir | ||
| + | if A[i,k]!=0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) | ||
| + | B[i] = B[i]-(B[k]*lam) | ||
| + | |||
| + | print ('matriks A :', '\n', A) | ||
| + | |||
| + | #3. back substitution | ||
| + | x=np.zeros (n,float) #menyatakan kalo dia matrix | ||
| + | for m in range (n-1, -1, -1) : #m dari bawah ke atas | ||
| + | x[m] = (B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m] | ||
| + | print ('nilai X', m+1, '=', x[m]) | ||
| + | |||
| + | Langkah pertama yang dilakukan reorder the equation dengan menukar baris pertama dengan baris ketiga karena apabila tidak dilakukan kita tidak dapat mengeliminasi dan membuat segitiga bawah. Selanjutnya line pertama sampah ketiga adalah kita mendefinisikan matriks tersebut dengan np.array dan ukuran matriksnya dengan len. Dari line 4 sampai 10 adalah eliminasi gaus untuk membentuk matriks segitiga bawah. for k adalah untuk menetukan baris pivotnya sedangkan for i adalah untuk baris yang akan dieliminasi oleh baris pivot. Range untuk menjelaskan koordinat dari pivot yaitu adalah baris pertama sampai 1 sebelum terakhir dan sisanya adalah baris dibawah pivot. If digunakan untuk memperintahkan apabila sudah 0 maka tidak perlu dieliminasi lagi. Lam adalah pengkali untuk pivot agar bisa mengeliminasi baris dibawahnya. perintah print untuk memunculkan matriks A setelah dieliminasi menjadi matriks segitiga bawah. Tahapan selanjutnya adalah back subtitution, yaitu untuk mencari nilai x. np.zeros digunakan untuk menyatakan bahwa nilai x adalah sebuah matriks kosong. Dengan menggunakan rumus matematis maka didapatkanlah nilai x. np.dot adalah dot product seperti pada aljabar linear. Print nilai X selesai. | ||
| + | |||
| + | [[Problem set 2.1 No.6]] | ||
| + | |||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | |||
| + | def diff_y (x,y): | ||
| + | diff_y = x**2 - 4*y | ||
| + | return (diff_y) | ||
| + | |||
| + | x = 0 | ||
| + | y = 1 | ||
| + | h = 0.01 | ||
| + | step_size = np.arange (0,0.03,h) | ||
| + | |||
| + | for t in step_size: | ||
| + | k1 = diff_y (x,y) | ||
| + | k2 = diff_y ((x+0.5*h), (y+0.5*k1*h)) | ||
| + | |||
| + | y = y + k1*h | ||
| + | |||
| + | print ('maka y(0.03) adalah', y) | ||
| + | |||
| + | Pertama kita definisikan turunan Y sebagai sebuah fungsi. Baris 4-7 adalah menjelaskan keadaan awal dimana keadaan yang ditanya adalah y saat x bernilai 0.03, maka pastinya dimulai dari angka 0 karena harus dilakukan step by step maka menggunakan step size dengan dimulai dari 0 sampai 0.03 dengan pertambahan sebesar h yaiu disini 0.01. Karena pada soal dijelaskan bahwa saat x nya bernilai 0, y nya bernilai 1 maka dituliskan seperti itu. Baris-baris selanjutnya adalah rumus runge kutta sampai 2nd order. Terakhir print nilai Y. Selesai. | ||
| + | |||
| + | [[Problem set 7.1 No.1]] | ||
| + | |||
| + | |||
| + | |||
| + | ''UTS'' | ||
| + | ------ | ||
| + | |||
| + | [[Soal A]] | ||
| + | |||
| + | [[Soal B]] | ||
| + | |||
| + | https://youtu.be/eis6-h4Ngf8 | ||
| + | |||
== Mekanika fluida == | == Mekanika fluida == | ||
Latest revision as of 22:34, 15 September 2024
Profil
Nama : Dika Auliady
NPM : 1706070671
Jurusan : Teknik Mesin
Biodata
Nama Lengkap : Dika Auliady
Tempat tanggal lahir : Jakarta
Alamat : BSD
Metode Numerik
Pertemuan 1 : 2 September 2019
Pada pertemuan pertama ini membahas tentang apa itu metode numerik. Metode numerik adalah mata kuliah yang mempelajari tentang bahasa pemrograman untuk bisa menyelesaikan sebuah persoalan dengan cara numerik bukan secara analitik. Karena pada kehidupan sehari-hari baik di teknik maupun bukan banyak permasalahan yang tidak bisa diselesaikan secara analitik. Contohnya untuk menyelesaikan sebuah persamaan di pegas dapat diselesaikan dengan mudah secara analitik namun, apabila pegas yang digunakan lebih banyak tentu menyelesaikannya akan lebih lama dan lebih sulit. Jadi untuk mengatasi ini, ada beberapa bahasa pemrograman sepeti python,matlab,C++, dan lain-lain untuk bisa menerjemahkan dari manusia ke komputer.
Phyton merupakan salah satu dari berbagai bahasa pemrograman yang berguna untuk mengkomunikasikan antara user dengan komputer. Dalam metode numerik bisa digunakan untuk menyelesaikan persoalan matematika yang rumit menjadi lebih mudah dan lebih cepat.
Mode interaktif merupakan fasilitas/fitur yang disediakan oleh Python sebagai tempat menulis kode secara interaktif. Fitur ini dikenal juga dengan Shell, Console, REPL (Read–Eval–Print Loop), interpreter, dsb. Cara membuka mode interaktif adalah dengan mengetik perintah python pada terminal.
Tanda >>>, artinya python siap menerima perintah. Terdapat juga tanda ... yang berarti secondary prompt atau sub prompt, biasanya muncul saat membuat blok kode dan menulis perintah tunggal dalam beberapa baris.perintah print, perintah ini berfungsi untuk mencetak teks ke layar.
Dari hasil diskusi pada pertemuan ini, bilangan eksak adalah bilangan yang pasti seperti 0,1,2 dan seterusnya merupakan 1. Hanya kesepakatan untuk mempermudah perhitungan dalam kehidupan 2. Merupakan pendekatan untuk menyelesaikan persoalan karena ada beberapa masalah yang tidak memiliki hasil atau tidak dapat terdefinisi hasilnya Jadi sebenarnya bilangan eksak itu tidak ada, dan menurut bahasanya eksak artinya adalah pasti maka sebenar-benarnya yang pasti hanyalah tuhan kita Allah saja.
Pertemuan 2 : 9 September 2019
Melanjutkan dari bahasan sebelumnya untuk mencari nilai dari hasil sebuah penyelesaian pada python perlu beberapa step dan tidak bisa langsung menggunakan satu perintah dan menemukan hasilnya, perlu menggunakan trial and error jadi alur pengerjaan pada python ini ada 3, yaitu algoritma,flowchart,code python. Untuk lebih jelasnya ada contoh soal yang diberikan seperti dibawah
def limit(x) :
try:
a = (x**2-1)
b = (x-1)
result = a/b
print (result)
except ZeroDivisonError :
c = ((x+(1/99))**2-1) / ((x+(1/99))-1)
print (c)
d = ((x+(1/999))**2-1) / ((x+(1/999))-1)
print (d)
e = ((x+(1/9999))**2-1) / ((x+(1/9999))-1)
print (e)
f = ((x+(1/99999))**2-1) / ((x+(1/99999))-1)
print (f)
g = ((x+(1/999999))**2-1) / ((x+(1/999999))-1)
print (g)
h = ((x+(1/9999999))**2-1) / ((x+(1/9999999))-1)
print (h)
Dari soal-soal limit ini tujuannya sama yaitu melakukan pendekatan untuk menemukan jawaban yang pasti dengan metode limit. pada persamaan pertama kita mau mendapatkan hasil terdefinisi maka untuk itu nilai x tidak boleh satu tetapi harus mendekati satu. Hasilnya dari 6 kali percobaan adalah mendekati angka 2. Kenapa menggunakan zerodivisonerror adalah agar untuk tidak terjadi eror angka 0. Cara pengerjaannya seperti biasa, pertama kita harus menjelaskan apa itu fungsi x lalu masukan perintah zerodivision eror dan print hasilnya.
Pertemuan 3 : 16 September 2019
- define fungsi T
def fungsi_T(x):
T = (x**2-1)/(x-1) return (T)
- 2 assign x = 0, delta_x = 0.1
x = 0 delta_x = 0.1 error = 1
To = fungsi_T(x)
print ('x adalah', x)
print ('Nilai T awal adalah', To)
x = x+delta_x
Tn = fungsi_T(x)
error = abs ((To-Tn/To))
print ('Nilai T selanjutnya', Tn)
print ('Error nya adalah', error)
x = x+delta_x
To = Tn
Tn = fungsi_T(x)
error = abs ((To-Tn/To))
print ('Nilai T selanjutnya', Tn)
print ('Error nya adalah', error)
Dalam menyelesaikan sebuah fungsi limit banyak cara yang bisa dilakukan. Pada pertemuan kali ini mempelajari tentang loop
yaitu apabila kita menginginkan sebuah hasil tetapi dengan syarat suatu kondisi maka cara dapat diterapkan.
Jadi dengan menggunakan soal di pertemuan sebelumnya, kita dapat menentukan syarat seperti apabila x nya masih kurang dari 1 maka perintah ini akan terus berjalan menyelesaikan persamaan atau dengan menggunakan errornya, karena error akan terus menuju 0. Untuk Tn adalah perbaharuan To atau T awal sementara delta_x adalah pertambahan yang kita inginkan untuk menuju ke 1 dimulai dari 0. Error adalah perbandingan selisih hasil fungsi yang baru dan yang lama.
Pertemuan 4 : 23 September 2019
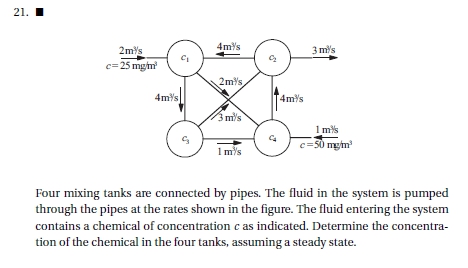
Pada pertemuan kali membahas tentang aplikasi pyhton pada sebuah sistem pipa. Sebelum itu kita harus mengetahui bentuk matematis dari soal yang dimaksud yaitu pada kasus ini dalam bentuk sebuah matriks. Penyelesaian matriks pada python dapat dikerjakan dengan eliminasi gauss. Berikut adalah langkah penyelesaiannya
Pertama mencari persamaan
6c1 - 4c2 = 50
-2c1 - c3 + 4c4 = 50
7c2 - 3c3 - 4c4 = 50
-4c1 + 4c3 = 50
Dalam bentuk matriks
[6. -4. 0. 0.]
[-4. 0. 4. 0.]
[-2. 0. -1. 4.]
[0. 7. -3. -4.]
Lalu masukan ke dalam code python
import numpy as np
A = np.array([[6,-4,0,0], [-4,0,4,0], [-2,0,-1,4], [0,7,-3,-4]], float)
B = np.array([50,0,50,0], float) print ('Matriks A adalah', A) print ('Matriks B adalah', B) n = len (A)
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
print ('Matriks A setelah eliminasi Gauss :', '\n', A)
x = np.zeros(n, float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
print ('Nilai X', m+1, '=', x[m])
Perintah untuk menerapkan numpy dalam coding ini agar mempermudah berbagai bentuk matematik digunakan dalam coding ini. Array berguna untuk membuat data yang dinginkan dituliskan dalam format matrix.Baris 2 dan 3 memunculkan matrix. Matrix yang muncul adalah matrix A dan B karena perintah print ditujukan kepada keduanya. Baris 4 dan 5 perintah menuliskan apa yang ada di dalamnya. Baris 6 mengetahui ukuran matriks dari A. Dalam kasus ini, nilai tersebut adalah 4x4. Float tidak termasuk jenis data lain karena itu berguna untuk mendefinisikan nilai desimal. Baris 7 -12 proses eliminasi bagian dari baris yang harusnya 0. Karena kita memerlukan matrix segitiga bawah untuk menyelesaikan dengan metode elimination gauss. For digunakan untuk menjalankan perintah hanya ketika argumen yang ada bersifat true. Proses yang berjalan adalah pengecekan setiap angka pada segitiga bawah dalam matrix tersebut agar nilainya menjadi 0. Baris 8 perintah for yang berarti hanya berjalan kalau argumennya bersifat true. Range disini berarti dimana kita akan memulai pivot. If digunakan untuk apabila nilai pada matriks sudah bernilai 0 maka diperlu lagi dilakukan pengoperasian. Lam merupakan pembagian nilai di koordinat data yang diberikan, setelah membentuk segitiga bawah nilai x dapat ditentukan. tetapi ada penggunaan np.dot disana. Baris 14 zero matrix yang berarti x adalah sebuah matrik yang kosong. Selanjutnya ada back subtitution. Perintah np.dot sama seperti dot product dalam aljabar linear. Baris terakhir print (x[m]). Selesai.
Pertemuan 6 : 7 Oktober 2019
Di pertemuan ini mempelajari tentang Runge-Kutta 4th order yaitu sebuah pendekatan dari sebuah grafik dengan menggunakan turunan keempat. Lebih jelasnya diajarkan dalam bentuk soal
Sebuah bola jatuh dengan kecepatan awal 0 pada jarak 100 m, hanya dipengaruhi percepatan gravitasi sebesar 10 m/s2 tentukan kecepatan dan tinggi bola setelah 4 detik
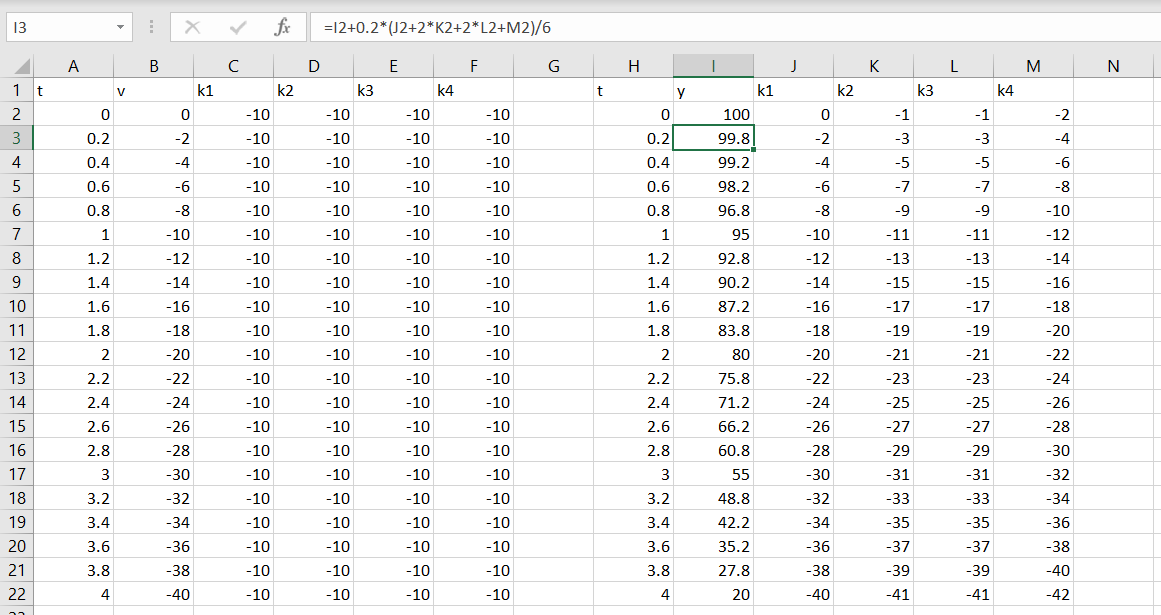
Pada pertemuan kali ini belum menggunakan python tetapi dengan excel agar pemahamannya lebih mudah. Yang pertama kali harus dilakukan adalah menentukan turunan pertama dari fungsi kecepatan dan fungsi posisi nya atau dv/dt dan dy/dt. Setelah mengetahui dv/dt = -g dan dy/dt = -gt maka hanya dengan memasukannya ke dalam rumus bisa didapatkaklah hasilnya.
Dengan h sebesar 0,2 artinya kita mencari data setiap 0,2 detik setelahnya sampai akhirnya di 4 detik karena ini merupakan pendekatan yang tidak bisa langsung mendapat hasilnya.
Pertemuan 7 : 14 Oktober 2019
Kuis metode numerik
import numpy as np
- 1. definisi matriks
A = np.array ([[1,2,0,-2,0], [0,1,0,2,-1], [0,0,2,1,2], [0,0,0,-1,1], [0,1,-1,1,-1]], float) B = np.array ([1,1,-4,-2,-1], float)
n = len(A)
- 2. eliminasi gauss
for k in range (0,n-1) : #k adalah baris pivot dimulai dari 0 sampai n-1
for i in range (k+1, n) : #i adalah baris dibawah pivot sampai terakhir
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
print ('matriks A :', '\n', A)
- 3. back substitution
x=np.zeros (n,float) #menyatakan kalo dia matrix for m in range (n-1, -1, -1) : #m dari bawah ke atas
x[m] = (B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m]
print ('nilai X', m+1, '=', x[m])
Langkah pertama yang dilakukan reorder the equation dengan menukar baris pertama dengan baris ketiga karena apabila tidak dilakukan kita tidak dapat mengeliminasi dan membuat segitiga bawah. Selanjutnya line pertama sampah ketiga adalah kita mendefinisikan matriks tersebut dengan np.array dan ukuran matriksnya dengan len. Dari line 4 sampai 10 adalah eliminasi gaus untuk membentuk matriks segitiga bawah. for k adalah untuk menetukan baris pivotnya sedangkan for i adalah untuk baris yang akan dieliminasi oleh baris pivot. Range untuk menjelaskan koordinat dari pivot yaitu adalah baris pertama sampai 1 sebelum terakhir dan sisanya adalah baris dibawah pivot. If digunakan untuk memperintahkan apabila sudah 0 maka tidak perlu dieliminasi lagi. Lam adalah pengkali untuk pivot agar bisa mengeliminasi baris dibawahnya. perintah print untuk memunculkan matriks A setelah dieliminasi menjadi matriks segitiga bawah. Tahapan selanjutnya adalah back subtitution, yaitu untuk mencari nilai x. np.zeros digunakan untuk menyatakan bahwa nilai x adalah sebuah matriks kosong. Dengan menggunakan rumus matematis maka didapatkanlah nilai x. np.dot adalah dot product seperti pada aljabar linear. Print nilai X selesai.
import numpy as np
def diff_y (x,y):
diff_y = x**2 - 4*y return (diff_y)
x = 0 y = 1 h = 0.01 step_size = np.arange (0,0.03,h)
for t in step_size:
k1 = diff_y (x,y) k2 = diff_y ((x+0.5*h), (y+0.5*k1*h)) y = y + k1*h
print ('maka y(0.03) adalah', y)
Pertama kita definisikan turunan Y sebagai sebuah fungsi. Baris 4-7 adalah menjelaskan keadaan awal dimana keadaan yang ditanya adalah y saat x bernilai 0.03, maka pastinya dimulai dari angka 0 karena harus dilakukan step by step maka menggunakan step size dengan dimulai dari 0 sampai 0.03 dengan pertambahan sebesar h yaiu disini 0.01. Karena pada soal dijelaskan bahwa saat x nya bernilai 0, y nya bernilai 1 maka dituliskan seperti itu. Baris-baris selanjutnya adalah rumus runge kutta sampai 2nd order. Terakhir print nilai Y. Selesai.
UTS