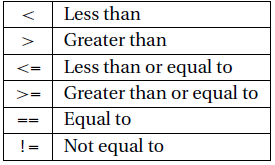Difference between revisions of "Adam Ilham Maulana"
Adamillana (talk | contribs) |
Adamillana (talk | contribs) |
||
| (64 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File:Adammm.PNG]] | + | [[File:Adammm.PNG|500px|thumb|right]] |
Nama : Adam Ilham Maulana | Nama : Adam Ilham Maulana | ||
| Line 8: | Line 8: | ||
| − | ''' | + | '''KENAPA MAHASISWA TEKNIK MESIN PERLU BELAJAR KALKULUS???''' |
---- | ---- | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
Agar mahasiswa Teknik Mesin dapat memiliki kemampuan berlogika dan mampu menyelesaikan masalah dengan cermat. | Agar mahasiswa Teknik Mesin dapat memiliki kemampuan berlogika dan mampu menyelesaikan masalah dengan cermat. | ||
| − | + | [[File:kalkulus.jpg]] | |
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | '''Tugas''' | ||
| + | |||
| + | 1. Pelajari Python! | ||
| + | |||
| + | 2. Buatlah penyelesaian pada soal yang ada di papan tulis! | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Python == | ||
| + | |||
| + | [[File:Python1.jpg]] | ||
| + | |||
| + | '''Pengertian''' | ||
| + | |||
| + | Python adalah bahasa pemrograman interpretatif multiguna dengan filosofi perancangan yang berfokus pada tingkat keterbacaan kode. Python diklaim sebagai bahasa yang menggabungkan kapabilitas, kemampuan, dengan sintaksis kode yang sangat jelas,dan dilengkapi dengan fungsionalitas pustaka standar yang besar serta komprehensif. | ||
| + | |||
| + | '''Sumber Belajar''' | ||
| + | - sololearn.com | ||
| + | - Buku numerical methods with Python 3 | ||
| + | |||
| + | |||
| + | == Proses Belajar Python == | ||
| + | |||
| + | '''1. Menulis Kalimat''' | ||
| + | |||
| + | >>> print('Hello world!') | ||
| + | |||
| + | Hello world! | ||
| + | |||
| + | |||
| + | '''2. Operasi sederhana''' | ||
| + | |||
| + | Operasi matemarikan yang dapat dilakukan menggunakan Python adalah Penjumlahan (+), pengurangan (-), perkalian (*), dan pembagian (/) | ||
| + | |||
| + | 1. Operasi Penjumlahan | ||
| + | |||
| + | >>> 2 + 2 | ||
| + | |||
| + | 4 | ||
| + | |||
| + | >>> 5 + 4 - 3 | ||
| + | |||
| + | 6 | ||
| + | |||
| + | |||
| + | 2. Operasi Pengurangan | ||
| + | |||
| + | >>> 5-3 | ||
| + | |||
| + | 2 | ||
| + | |||
| + | |||
| + | 3. Perkalian dan pembagian. | ||
| + | |||
| + | >>> 2 * (3 + 4) | ||
| + | |||
| + | 14 | ||
| + | |||
| + | >>> 10 / 2 | ||
| + | |||
| + | 5.0 | ||
| + | |||
| + | - pembagian oleh bilangan 0 akan menyebabkan error - | ||
| + | |||
| + | >>> 11 / 0 | ||
| + | |||
| + | Traceback (most recent call last): | ||
| + | |||
| + | File "<stdin>", line 1, in <module> | ||
| + | |||
| + | ZeroDivisionError: division by zero | ||
| + | |||
| + | |||
| + | |||
| + | '''3. Floats''' | ||
| + | |||
| + | Floats digunakan dalam Python untuk mewakili angka yang bukan bilangan bulat. | ||
| + | |||
| + | >>> 3/4 | ||
| + | |||
| + | 0.75 | ||
| + | |||
| + | >>> 9.8765000 | ||
| + | |||
| + | 9.8765 | ||
| + | |||
| + | |||
| + | |||
| + | '''4. eksponen (perpangkatan)''' | ||
| + | |||
| + | >>> 2**5 | ||
| + | |||
| + | 32 | ||
| + | |||
| + | >>> 9 ** (1/2) | ||
| + | |||
| + | 3.0 | ||
| + | |||
| + | |||
| + | '''5. Quotient dan remainder''' | ||
| + | |||
| + | Untuk menentukan hasil bagi dan sisa divisi, masing-masing menggunakan divisi lantai dan operator modulo. | ||
| + | Pembagian lantai dilakukan dengan menggunakan dua garis miring ke depan (//). | ||
| + | Operator modulo dijalankan dengan simbol persen (%). | ||
| + | Operator ini dapat digunakan dengan float dan integer. | ||
| + | |||
| + | >>> 20 // 6 | ||
| + | |||
| + | 3 | ||
| + | |||
| + | >>> 1.25 % 0.5 | ||
| + | |||
| + | 0.25 | ||
| + | |||
| + | |||
| + | '''6. menulis kalimat dengan tanda petik.''' | ||
| + | |||
| + | >>> "Python is fun!" | ||
| + | |||
| + | 'Python is fun!' | ||
| + | |||
| + | >>> 'Always look on the bright side of life' | ||
| + | |||
| + | 'Always look on the bright side of life' | ||
| + | |||
| + | |||
| + | '''7. Tuple''' | ||
| + | |||
| + | Sebuah tuple adalah urutan objek yang dipisahkan oleh koma dan terlampir | ||
| + | dalam kurung. Jika tuple berisi objek tunggal, koma akhir diperlukan; | ||
| + | misalnya, x = (2,). Tuples mendukung operasi yang sama dengan string; mereka | ||
| + | juga tidak berubah. Berikut adalah contoh di mana tuple rec berisi tuple lain | ||
| + | (25,05,2000): | ||
| + | |||
| + | contohnya. | ||
| + | |||
| + | |||
| + | >>>rec = ("Adam", "Ilham", "Maulana", (25, 5, 2000)) | ||
| + | |||
| + | >>>NamaDepan, NamaTengah, NamaAkhir, TglLahir = rec | ||
| + | |||
| + | >>>print (NamaDepan) | ||
| + | |||
| + | Adam | ||
| + | |||
| + | >>>Bulanlahir = TglLahir [1] | ||
| + | |||
| + | >>>print (Bulanlahir) | ||
| + | |||
| + | 5 | ||
| + | |||
| + | >>>nama = rec[1]+ ' ' + rec[2] + ' ' + rec[0] | ||
| + | |||
| + | >>>print (nama) | ||
| + | |||
| + | Ilham Maulana Adam | ||
| + | |||
| + | |||
| + | '''8. Comparison Opereators''' | ||
| + | |||
| + | Operator perbandingan (relasional) mengembalikan Benar atau Salah. Operator-operator ini antara lain. | ||
| + | |||
| + | [[File:Haha.PNG|800px|thumb|center|]] | ||
| + | |||
| + | >>> a = 2 | ||
| + | |||
| + | >>> b = 1.99 | ||
| + | |||
| + | >>> c = ’2’ | ||
| + | |||
| + | >>> print(a > b) | ||
| + | |||
| + | True | ||
| + | |||
| + | >>> print(a == c) | ||
| + | |||
| + | False | ||
| + | |||
| + | >>> print((a > b) and (a != c)) | ||
| + | |||
| + | True | ||
| + | |||
| + | >>> print((a > b) or (a == b)) | ||
| + | |||
| + | True | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | == Menyelesaikan tugas 1 dengan Python == | ||
| + | |||
| + | '''1. Membuka IDLE (Python)''' | ||
| + | |||
| + | '''2. Masukan codes''' | ||
| + | |||
| + | [[File:aabb.PNG]] | ||
| + | |||
| + | 1. import sympy | ||
| + | |||
| + | memasukan modul sympy | ||
| + | |||
| + | |||
| + | 2. x = sympy.symbol('x') | ||
| + | |||
| + | mendefinisikan x sebagai symbol | ||
| + | |||
| + | |||
| + | 3. fungsi = (x**2-1)/(x-1) | ||
| + | |||
| + | menyimpan perhitungan dalam variabel fungsi. | ||
| + | |||
| + | |||
| + | 4. hasil = sympy.limit(fungsi, x, 1) | ||
| + | |||
| + | menyimpan hasil perhitungan dalam variabel hasil. | ||
| + | |||
| + | |||
| + | 5. print(hasil) | ||
| + | |||
| + | |||
| + | |||
| + | '''3. Press F5''' | ||
| + | |||
| + | hasil akan muncul. | ||
| + | |||
| + | [[File:bbcc.PNG|800px|thumb|center]] | ||
| + | |||
| + | |||
| + | |||
| + | == Pertemuan Kedua == | ||
| + | |||
| + | '''1. Cara membuat nama dan tanggal lahir''' | ||
| + | |||
| + | 1. rec = ('Adam', 'Ilham', 'Maulana',(25,5,2000)) | ||
| + | |||
| + | 2. NamaAwal, NamaTengah, NamaAkhir, tanggallahir = rec | ||
| + | |||
| + | 3. print(NamaTengah) | ||
| + | |||
| + | 4. TahunLahir = tanggallahir [2] | ||
| + | |||
| + | 5. print(TahunLahir) | ||
| + | |||
| + | 6. name = rec[0] +''+rec[1] | ||
| + | |||
| + | 7. print(name) | ||
| + | |||
| + | 5. print(rec[0:3]) | ||
| + | |||
| + | |||
| + | [[File:T2.PNG|800px|thumb|center]] | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | == Cara mengerjakan deret fibonacci dengan python == | ||
| + | |||
| + | |||
| + | '''1. metode loop (while/for)''' | ||
| + | |||
| + | [[File:Codesfibo1.PNG|500px|thumb|center]] | ||
| + | |||
| + | ket: untuk menetukan suku keberapa tinggal ubah nNum: | ||
| + | (disini saya mencoba menemukan suke ke 10 untuk deret fibonacci yang dimulai dari 1) | ||
| + | |||
| + | setelah itu jalankan. | ||
| + | |||
| + | [[File:Hasilfibo1.PNG|500px|thumb|center]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''2. metode function''' | ||
| + | |||
| + | [[File:Codesfibo2.PNG|500px|thumb|center]] | ||
| + | |||
| + | kemudian jalankan | ||
| + | |||
| + | [[File:Codesfibo2.2.PNG|500px|thumb|center]] | ||
| + | |||
| + | setelah dijalankan kemudian tentukan suku keberapa (disini saya mencari suku ke 15) | ||
| + | |||
| + | [[File:Hasilfibo2.PNG|500px|thumb|center]] | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | == belajar mengaplikasikan meode numerik dengan python == | ||
| + | |||
| + | - numpy merupakan library yang ada di python | ||
| + | - fungsi eval merubah string jadi number. | ||
| + | - ni adalah jumlah node | ||
| + | - np.zeros((ni,ni),float) membentuk matriks isinya 0 ukurannya ni*ni. | ||
| + | - n_k adalah matriks yang isinya data data dari konstanta pegas | ||
| + | |||
| + | |||
| + | == aplikasi differensial dengan metode numerik == | ||
| + | |||
| + | terlebih dahulu kita harus membuat model sebelum melakukan komputasi dalam komputer | ||
| + | |||
| + | metode numerik dalam teknik mesin ada 3 aspek | ||
| + | |||
| + | seorang engineer adalah bagaimana caranya untuk memodelkan | ||
| + | |||
| + | lalu bagaimana caranya memodelkan suatu barang yang natinya dapat digunakan secara continu. misalnya ada sebuah benda diberikan gaya kemudian benda itu memiliki massa dan gaya itu terdistribusi ke seluruh bagian benda itu. dan itu yang dinamakan continu. melalui sifat continu dapat diterapkan beberapa hukum dalam sebuah benda contohnya, akan menghasilkan model matematis | ||
| + | |||
| + | '''metode runge kutta''' | ||
| + | |||
| + | slah satu metode untuk memnyelesaikan persamaan differensial. | ||
| + | |||
| + | |||
| + | |||
| + | == Jawaban quiz == | ||
| + | |||
| + | |||
| + | '''a. problem set 2.1 nomer 6 halaman 55''' | ||
| + | |||
| + | # Definisikan Matriks A | ||
| + | A = np.array([[0, 0, 2, 1, 2], | ||
| + | [0, 1, 0, 2, -1], | ||
| + | [1, 2, 0, -2, 0], | ||
| + | [0, 0, 0, -1, 1], | ||
| + | [0, 1, -1, 1, -1]], float) | ||
| + | |||
| + | #Definisikan Matriks B | ||
| + | b = np.array([[1], | ||
| + | [1], | ||
| + | [-4], | ||
| + | [-2], | ||
| + | [-1]],float) | ||
| + | |||
| + | Ab = np.hstack([A, b]) | ||
| + | print (Ab, "\n") | ||
| + | |||
| + | n = len(b) | ||
| + | |||
| + | |||
| + | #Fase Eliminasi | ||
| + | for i in range(0, n-1): | ||
| + | for j in range(i + 1, n): | ||
| + | lam = Ab[i,i] / Ab[j,i] | ||
| + | Ab[j] = Ab[i] - lam * Ab[j] | ||
| + | |||
| + | print ("Hasil Fase Eliminasi \n", Ab, "\n") | ||
| + | |||
| + | #Fase Substitusi | ||
| + | for i in range(n - 1, -1, -1): | ||
| + | Ab[i] = Ab[i] / Ab[i, i] | ||
| + | for j in range(i - 1, -1, -1): | ||
| + | b = Ab[j] | ||
| + | lam = Ab[i,i] / Ab[j,i] | ||
| + | Ab[j] = Ab[i] - lam * Ab[j] | ||
| + | |||
| + | print ("Hasil Fase Substitusi \n", Ab, "\n") | ||
| + | |||
| + | x = Ab[:, 5] | ||
| + | |||
| + | print ("nilai xnya adalah \n", x) | ||
| + | |||
| + | |||
| + | '''cara kedua''' | ||
| + | |||
| + | from numpy import linalg | ||
| + | import numpy as np | ||
| + | |||
| + | #definisikan matriks A | ||
| + | A1 = [0, 0, 2, 1, 2] | ||
| + | A2 = [0, 1, 0, 2, -1] | ||
| + | A3 = [1, 2, 0, -2, 0] | ||
| + | A4 = [0, 0, 0, -1, 1] | ||
| + | A5 = [0, 1, -1, 1, -1] | ||
| + | |||
| + | nmat = np.array ([A1, A2, A3, A4, A5]) | ||
| + | |||
| + | #definisikan matriks B | ||
| + | B = np.array ([1, 1, -4, -2, -1]) | ||
| + | |||
| + | #Dibawah ini adalah kode untuk memecahkan persamaan aljabar linear bertuliskan (linalg) | ||
| + | jawaban = linalg.solve (nmat,B) | ||
| + | a = int(jawaban[0]) | ||
| + | b = int(jawaban[1]) | ||
| + | c = int(jawaban[2]) | ||
| + | d = int(jawaban[3]) | ||
| + | f = int(jawaban[4]) | ||
| + | |||
| + | #munculkan hasil | ||
| + | print("X1 adalah ", a) | ||
| + | print("X2 adalah ", b) | ||
| + | print("X3 adalah ", c) | ||
| + | print("X4 adalah ", d) | ||
| + | print("X5 adalah ", f) | ||
| + | |||
| + | #maka dari cara kedua didapat matriks Xnya adalah | ||
| + | X1 adalah 2 | ||
| + | |||
| + | X2 adalah -2 | ||
| + | |||
| + | X3 adalah 1 | ||
| + | |||
| + | X4 adalah 1 | ||
| + | |||
| + | X5 adalah -1 | ||
| + | |||
| + | |||
| + | |||
| + | '''b. problem nomer 2 halaman 263''' | ||
| + | |||
| + | |||
| + | # Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01. | ||
| + | x0 = 2 | ||
| + | |||
| + | y = 1 | ||
| + | h = 0.01 | ||
| + | x = float(input("Masukkan nilai t: ")) | ||
| + | if x>0 : | ||
| + | # dydx menyatakan persamaan awal dalam soal. | ||
| + | # Didapat hasil x^2-4y | ||
| + | |||
| + | def dydx(x, y): | ||
| + | return (x**2-4*y) | ||
| + | |||
| + | # Ini merupakan implementasi perhitungan Runge-Kutta. | ||
| + | def rungeKutta(x0, y0, x, h): | ||
| + | n = (int)((x - x0)/h) | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | k1 = h * dydx(x0, y) | ||
| + | k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * dydx(x0 + h, y + k3) | ||
| + | |||
| + | # untuk y selanjutnya | ||
| + | y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | |||
| + | # untuk x selanjutnya | ||
| + | x0 = x0 + h | ||
| + | list.append(y) | ||
| + | return y | ||
| + | print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h)) | ||
| + | |||
| + | kemudian akan didapatkan hasil apabila t=0.03 | ||
| + | |||
| + | |||
| + | Masukkan nilai t: 0.03 | ||
| + | |||
| + | Nilai y pada t = 0.03 adalah 1 | ||
| + | |||
| + | |||
| + | |||
| + | == Ujian Tengah semester == | ||
| + | |||
| + | |||
| + | '''Soal nomer satu''' | ||
| + | |||
| + | ''Input'' | ||
| + | |||
| + | # -*- coding: utf-8 -*- | ||
| + | """ | ||
| + | Created on Wed Oct 23 13:30:54 2019 | ||
| + | |||
| + | @author: Adam Ilham Maulana | ||
| + | """ | ||
| + | |||
| + | #Bismillahirrahmanirrahim | ||
| + | |||
| + | #soal nomer 1. carilah tegangan tali. | ||
| + | import math | ||
| + | |||
| + | #Tentukan variabel-variabel yang akan digunakan dalam perhitungan | ||
| + | |||
| + | g=9.81 | ||
| + | |||
| + | M1=eval(input("besar massa benda 1 ?")) #masukkan 30 kg | ||
| + | |||
| + | M2=eval(input("besar massa benda 2 ?")) #masukkan 20 kg | ||
| + | |||
| + | M3=eval(input("besar massa benda 3 ?")) #masukkan 10 kg | ||
| + | |||
| + | k1=eval(input("Koefisien gesek benda 1 ?")) #masukkan 0.6 | ||
| + | |||
| + | k2=eval(input("koefisien gesek benda 2 ?")) #masukkan 0.4 | ||
| + | |||
| + | k3=eval(input("Koefisien gesek benda 3 ?")) #masukkan 0.2 | ||
| + | |||
| + | alfa=eval(input("sudutnya kemiringan ?")) #masukkan 60 | ||
| + | |||
| + | a=eval(input("percepatan :")) #masukkan 5 m/s^2 | ||
| + | |||
| + | |||
| + | x= math.sin(alfa) | ||
| + | |||
| + | y= math.cos(alfa) | ||
| + | |||
| + | #buat rumus untuk mencari Tegangan tali 1, 2, dan 3 | ||
| + | |||
| + | T1=M1*g*(x-k1*y)-M1*a | ||
| + | |||
| + | T2=M2*g*(x-k2*y)+T1-M2*a | ||
| + | |||
| + | T3=M3*g*(x-k3*y)+T2-M3*a | ||
| + | |||
| + | |||
| + | |||
| + | #akan didapatkan hasilnya | ||
| + | |||
| + | print ("tegangan tali T1 adalah", abs(T1)) | ||
| + | |||
| + | print ("tegangan tali T2 adalah", abs(T2)) | ||
| + | |||
| + | print ("tegangan Tali T2 adalah", abs(T3)) | ||
| + | |||
| + | |||
| + | ''output'' | ||
| + | |||
| + | runfile('E:/Adam Ilham Maulana/Universitas Indonesia/metnum/untitled3.py', wdir='E:/Adam Ilham Maulana/Universitas Indonesia/metnum') | ||
| + | |||
| + | besar massa benda 1 ? 30 | ||
| + | |||
| + | besar massa benda 2 ? 20 | ||
| + | |||
| + | besar massa benda 3 ? 10 | ||
| + | |||
| + | Koefisien gesek benda 1 ? 0.6 | ||
| + | |||
| + | koefisien gesek benda 2 ? 0.4 | ||
| + | |||
| + | Koefisien gesek benda 3 ? 0.2 | ||
| + | |||
| + | sudutnya kemiringan ? 60 | ||
| + | |||
| + | percepatan : 5 | ||
| + | |||
| + | |||
| + | |||
| + | dapat hasilnya | ||
| + | |||
| + | |||
| + | tegangan tali T1 adalah 71.52868170867406 | ||
| + | |||
| + | tegangan tali T2 adalah 156.5871548659475 | ||
| + | |||
| + | tegangan Tali T2 adalah 217.80273412032957 | ||
| + | |||
| + | [[File:Soal1.mp4]] | ||
| + | |||
| + | |||
| + | |||
| + | '''soal nomer 2''' | ||
| + | |||
| + | #definisikan variabel-variabel yang akan digunakan | ||
| + | |||
| + | g = 9.81 | ||
| + | |||
| + | densitas = 1.2 #merupakan massa jenis udara | ||
| + | |||
| + | cd = eval(input("koefisien drag:")) | ||
| + | |||
| + | area = eval(input("luas (m^2):")) | ||
| + | |||
| + | v1 = eval(input("kecepatan yang diinginkan:")) | ||
| + | |||
| + | m = eval(input("massa mobil(kg):")) | ||
| + | |||
| + | u = eval(input("koefisien gesek:")) | ||
| + | |||
| + | a = eval(input("percepatan(m/s^2):")) | ||
| + | |||
| + | |||
| + | #cari percepatan yang disebabkan gaya gesek (ag) dan yang disebabkan oleh gaya hambat udara (adrag) | ||
| + | |||
| + | ag = g*u | ||
| + | |||
| + | for v0 in range (0,v1): | ||
| + | |||
| + | adrag = (cd*area*densitas*v0**2)/2*m | ||
| + | |||
| + | atot = a - (adrag + ag) #berasal dari rumus Ftot/massa total | ||
| + | |||
| + | |||
| + | #masukkan rumus untuk mendapatkan waktu yg diperlukan | ||
| + | |||
| + | t = -(v1)/atot | ||
| + | |||
| + | #kemudian didapatkan waktu yang diperlukan untuk mencapai kecepatan tertentu | ||
| + | |||
| + | print("waktu yang diperlukan untuk mencapai kecepatan yang diinginkan:", t, "sekon") | ||
| + | |||
| + | [[File:Soal2.mp4]] | ||
| + | |||
| + | |||
| + | |||
| + | [[Video Muhasabah]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Contoh Soal Runge kutta == | ||
| + | |||
| + | '''intro''' | ||
| + | |||
| + | Rasulullah SAW. menganjurkan umat muslim untuk memanah. kemudian beliau bersabda. | ||
| + | |||
| + | “Sesungguhnya ia mengatakan, “Barangsiapa telah mengetahui tentang memanah kemudian meninggalkannya, maka dia bukan termasuk golonganku, atau telah bermaksiat.” (HR. Muslim) | ||
| + | |||
| + | |||
| + | |||
| + | '''soal''' | ||
| + | |||
| + | sebuah anak panah dilontarkan dari keadaan diam, dengan massa 0.2 kg. dan kaliber 3 cm dan diketahuai gaya koefisien drag dari udara sebesar 0.1 dan memiliki percepatan. diketahuai F sebesar 800t N pada saat 0=<t<0.5 dan F sebesar 800 pada saat t>=0.5 | ||
| + | |||
| + | tentukan kecepatan laju anak panah pada saat anak panah tersebut pada waktu 2 s!! | ||
| + | |||
| + | |||
| + | '''penyelesaian dengan rumus rungue kutta''' | ||
| + | |||
| + | # -*- coding: utf-8 -*- | ||
| + | """ | ||
| + | Created on Wed Nov 6 15:08:38 2019 | ||
| + | |||
| + | @author: USER | ||
| + | """ | ||
| + | |||
| + | |||
| + | #pendefinisian soal | ||
| + | # t0 dan v0 sebagai keadaan awal, t sebagai t yang diinput, dan h sebagai increment | ||
| + | t0 = 0 | ||
| + | v0 = 0 | ||
| + | h = 0.01 # di sini digunakan h = 0.01 | ||
| + | t = float(input("masukkan nilai t: ")) # perintah untuk memasukkan nilai t | ||
| + | |||
| + | if 0 <= t < 0.5: # untuk 0 <= t < 0.2 | ||
| + | def F(t, v): | ||
| + | return (4000 * t - 0.0001125 * (v**2)) # persamaan a yang diperoleh dari soal. | ||
| + | |||
| + | #metode runge kutta | ||
| + | def rungeKutta(t0, v0, t, h): | ||
| + | n = (int)((t - t0) / h) | ||
| + | v = v0 | ||
| + | for i in range(1, n + 1): | ||
| + | k1 = h * F(t0, v) | ||
| + | k2 = h * F(t0 + 0.5 * h, v + 0.5 * k1) | ||
| + | k3 = h * F(t0 + 0.5 * h, v + 0.5 * k2) | ||
| + | k4 = h * F(t0 + h, v + k3) | ||
| + | v = v + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | t0 = t0 + h | ||
| + | return v | ||
| + | |||
| + | print("Nilai v pada t =", t, "adalah", rungeKutta(t0, v0, t, h), "m/s") # nilai v akan muncul sesuai dengan t yang dimasukkan | ||
| + | |||
| + | elif t >= 0.1: # untuk t >= 0.1 | ||
| + | def F(t, v): | ||
| + | return (4000 - 0.0001125 * (v**2)) # persamaan a yang telah diperoleh | ||
| + | |||
| + | def rungeKutta(t0, v0, t, h): # perhitungan Runge-Kutta | ||
| + | n = (int)((t - t0) / h) | ||
| + | v = v0 | ||
| + | for i in range(1, n + 1): | ||
| + | k1 = h * F(t0, v) | ||
| + | k2 = h * F(t0 + 0.5 * h, v + 0.5 * k1) | ||
| + | k3 = h * F(t0 + 0.5 * h, v + 0.5 * k2) | ||
| + | k4 = h * F(t0 + h, v + k3) | ||
| + | v = v + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | t0 = t0 + h | ||
| + | return v | ||
| + | |||
| + | print("Nilai v pada t =", t, "adalah", rungeKutta(t0, v0, t, h), "m/s") # nilai v akan muncul sesuai dengan nilai t yang dimasukkan | ||
| + | |||
| + | else: | ||
| + | print("Nilai t harus positif.") | ||
| + | |||
| + | |||
| + | |||
| + | == Curve fitting == | ||
| + | |||
| + | curve fitting dibagi jadi dua | ||
| + | |||
| + | - regresi. | ||
| + | |||
| + | konsep yangpaling m,udah adalah regresi linear. garis yang mendekati adalah yang memiliki error paling kecil. | ||
| + | |||
| + | |||
| + | |||
| + | - interpolasi | ||
| + | |||
| + | |||
| + | == Optimasi == | ||
| + | |||
| + | Untuk tugas ini, kami menggunakan referensi airfoil NACA-0009 9.0% smoothed untuk mendapatkan nilai drag force dan lift force pada kecepatan 30 m/s | ||
| + | |||
| + | |||
| + | [[File:Airfoil Kel.12.png]] | ||
| + | |||
| + | |||
| + | Variabel pada tugas ini adalah angle airfoil dari -15° hingga 90° | ||
| + | |||
| + | dengan bantuan aplikasi CFDSOF dan Paraview | ||
| + | |||
| + | didapatkan nilai-nilai sebagai berikut | ||
| + | |||
| + | |||
| + | [[File:Data Airfoil Kel.12.png]] | ||
| + | |||
| + | |||
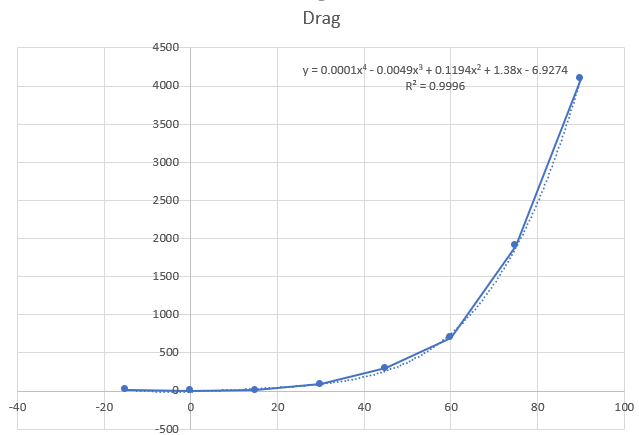
| + | '''Grafik Drag''' | ||
| + | |||
| + | [[File:Grafik Drag versi 2 Kel.12.png]] | ||
| + | |||
| + | |||
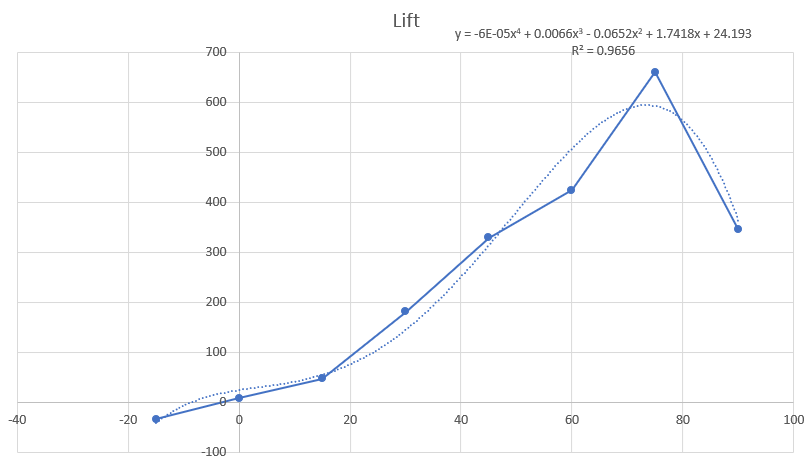
| + | '''Grafik Lift''' | ||
| + | |||
| + | [[File:Grafik Lift versi 2 Kel.12.png]] | ||
| + | |||
| + | |||
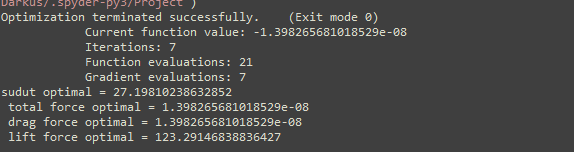
| + | '''Hasil Optimasi''' | ||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | def drag(x):#drag | ||
| + | x = x[0] | ||
| + | d = 0.0001*x**4 -0.0049*x**3 + 0.1194*x**2 - 1.38*x - 6.927 | ||
| + | return d | ||
| + | |||
| + | def lift(x): #lift | ||
| + | x = x[0] | ||
| + | l = -0.00006*x**4 + 0.0066*x**3 - 0.0652*x**2 + 1.7418*x + 24.193 | ||
| + | return l | ||
| + | |||
| + | def obj(x): #sudut yang diminimalkan | ||
| + | return drag(x) | ||
| + | |||
| + | def c1(x): #variable SUDUT yang meminimalkan persamaan garis drag | ||
| + | return drag(x) | ||
| + | def c2(x): #variable SUDUT yang meminimalkan persamaan garis lift | ||
| + | return lift(x) | ||
| + | |||
| + | |||
| + | con1=({'type':'ineq','fun':c1}) | ||
| + | con2=({'type':'ineq','fun':c2}) | ||
| + | cons = (con1,con2) | ||
| + | |||
| + | a = (10,90) | ||
| + | batas = [a] | ||
| + | |||
| + | x1_guess = 20 | ||
| + | |||
| + | x0 = np.array([x1_guess]) | ||
| + | |||
| + | sol = minimize(obj,x0, method='SLSQP', bounds=batas, constraints=cons, options={'disp':True}) | ||
| + | |||
| + | xopt = sol.x | ||
| + | fopt = -sol.fun | ||
| + | |||
| + | dopt = drag(xopt) # drag optimal | ||
| + | lopt = lift(xopt) # lift optimal | ||
| + | |||
| + | print ('sudut optimal = '+str(xopt[0]), "\n", 'total force optimal = '+str(fopt), "\n", 'drag force optimal = '+str(-dopt), "\n", 'lift force optimal = '+str(lopt)) | ||
| + | |||
| + | |||
| + | [[File:Optimasi Elvin 1.png]] | ||
| + | |||
| + | |||
| + | |||
| + | == Aplikasi ANN pada Data CFD == | ||
| + | |||
| + | '''Koding ANN (Dengan Google Colab)''' | ||
| + | |||
| + | import tensorflow as tf | ||
| + | from tensorflow import keras | ||
| + | from tensorflow.keras import Sequential | ||
| + | from tensorflow.keras.layers import Flatten, Dense | ||
| + | import numpy as np | ||
| + | import pandas as pd | ||
| + | print(tf.__version__) | ||
| + | |||
| + | from google.colab import files | ||
| + | uploaded = files.upload() | ||
| + | |||
| + | import io | ||
| + | database = pd.read_excel(io.BytesIO(uploaded['ANN ELVIN.xlsx'])) | ||
| + | |||
| + | x = database['angle of attack'] | ||
| + | #y1 = dataset['Fdrag'] | ||
| + | #y2 = dataset['Flift'] | ||
| + | y = database['drag/lift'] | ||
| + | |||
| + | import matplotlib.pyplot as plt | ||
| + | plt.plot(x,y) | ||
| + | |||
| + | norm_x = [(a-np.min(x))/(np.max(x)-np.min(x)) | ||
| + | for a in x] | ||
| + | norm_y = [(a-np.min(y))/(np.max(y)-np.min(y)) | ||
| + | for a in y] | ||
| + | |||
| + | from sklearn.preprocessing import StandardScaler | ||
| + | from sklearn.model_selection import train_test_split | ||
| + | |||
| + | x_train, x_test, y_train, y_test = train_test_split(norm_x, norm_y, test_size = 0.3, random_state = | ||
| + | 0) | ||
| + | |||
| + | x_train = np.asarray(x_train) | ||
| + | x_test = np.asarray (x_test) | ||
| + | y_train = np.asarray (y_train) | ||
| + | y_test = np.asarray (y_test) | ||
| + | |||
| + | |||
| + | import matplotlib.pyplot as plt | ||
| + | unnorm_y_awal= [a*(np.max(y)-np.min(y))+np.min(y) | ||
| + | for a in y_test] | ||
| + | plt.suptitle('Output Real') | ||
| + | plt.plot(unnorm_y_awal) | ||
| + | |||
| + | model = Sequential() | ||
| + | model.add(Dense(3, activation='relu', input_dim = 1)) # input layer | ||
| + | model.add(Dense(4, activation='relu')) # hidden layer | ||
| + | model.add(Dense(1, activation = 'sigmoid')) | ||
| + | |||
| + | model.compile(optimizer='adam', loss = 'binary_crossentropy', metrics=['accuracy']) | ||
| + | |||
| + | history = model.fit(x_train, y_train, batch_size = 64, epochs = 5, verbose = 1, validation_split = 0.16) | ||
| + | |||
| + | Train on 3 samples, validate on 1 samples | ||
| + | Epoch 1/5 | ||
| + | 3/3 [==============================] - 0s 34ms/sample - loss: 0.7800 - acc: 0.0000e+00 - val_loss: 0.8347 - val_acc: 0.0000e+00 | ||
| + | Epoch 2/5 | ||
| + | 3/3 [==============================] - 0s 2ms/sample - loss: 0.7782 - acc: 0.0000e+00 - val_loss: 0.8323 - val_acc: 0.0000e+00 | ||
| + | Epoch 3/5 | ||
| + | 3/3 [==============================] - 0s 1ms/sample - loss: 0.7765 - acc: 0.0000e+00 - val_loss: 0.8299 - val_acc: 0.0000e+00 | ||
| + | Epoch 4/5 | ||
| + | 3/3 [==============================] - 0s 1ms/sample - loss: 0.7748 - acc: 0.0000e+00 - val_loss: 0.8275 - val_acc: 0.0000e+00 | ||
| + | Epoch 5/5 | ||
| + | 3/3 [==============================] - 0s 2ms/sample - loss: 0.7731 - acc: 0.0000e+00 - val_loss: 0.8252 - val_acc: 0.0000e+00 | ||
| + | |||
| + | unnorm_x= [a*(np.max(x)-np.min(x))+np.min(x) | ||
| + | for a in x_test] | ||
| + | unnorm_y= [a*(np.max(y)-np.min(y))+np.min(y) | ||
| + | for a in y_test] | ||
| + | |||
| + | plt.suptitle('Output Real vs Output Prediction ANN') | ||
| + | plt.subplot(2, 1, 1) | ||
| + | plt.plot(unnorm_y_awal) | ||
| + | plt.subplot(2, 1, 2) | ||
| + | plt.plot(unnorm_y) | ||
| + | |||
| + | |||
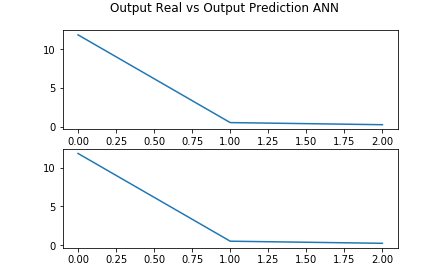
| + | '''Hasil''' | ||
| + | |||
| + | Dapat dilihat bahwa output real dengan output prediction ANN sama persis | ||
| − | [[File: | + | [[File:ANN Elvin 1.png]] |
Latest revision as of 17:13, 17 December 2019
Nama : Adam Ilham Maulana
NPM : 1806201251
Jurusan : Teknik Mesin
KENAPA MAHASISWA TEKNIK MESIN PERLU BELAJAR KALKULUS???
Agar mahasiswa Teknik Mesin dapat memiliki kemampuan berlogika dan mampu menyelesaikan masalah dengan cermat.
Tugas
1. Pelajari Python!
2. Buatlah penyelesaian pada soal yang ada di papan tulis!
Contents
- 1 Python
- 2 Proses Belajar Python
- 3 Menyelesaikan tugas 1 dengan Python
- 4 Pertemuan Kedua
- 5 Cara mengerjakan deret fibonacci dengan python
- 6 belajar mengaplikasikan meode numerik dengan python
- 7 aplikasi differensial dengan metode numerik
- 8 Jawaban quiz
- 9 Ujian Tengah semester
- 10 Contoh Soal Runge kutta
- 11 Curve fitting
- 12 Optimasi
- 13 Aplikasi ANN pada Data CFD
Python
Pengertian
Python adalah bahasa pemrograman interpretatif multiguna dengan filosofi perancangan yang berfokus pada tingkat keterbacaan kode. Python diklaim sebagai bahasa yang menggabungkan kapabilitas, kemampuan, dengan sintaksis kode yang sangat jelas,dan dilengkapi dengan fungsionalitas pustaka standar yang besar serta komprehensif.
Sumber Belajar - sololearn.com - Buku numerical methods with Python 3
Proses Belajar Python
1. Menulis Kalimat
>>> print('Hello world!')
Hello world!
2. Operasi sederhana
Operasi matemarikan yang dapat dilakukan menggunakan Python adalah Penjumlahan (+), pengurangan (-), perkalian (*), dan pembagian (/)
1. Operasi Penjumlahan
>>> 2 + 2
4
>>> 5 + 4 - 3
6
2. Operasi Pengurangan
>>> 5-3
2
3. Perkalian dan pembagian.
>>> 2 * (3 + 4)
14
>>> 10 / 2
5.0
- pembagian oleh bilangan 0 akan menyebabkan error -
>>> 11 / 0
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ZeroDivisionError: division by zero
3. Floats
Floats digunakan dalam Python untuk mewakili angka yang bukan bilangan bulat.
>>> 3/4
0.75
>>> 9.8765000
9.8765
4. eksponen (perpangkatan)
>>> 2**5
32
>>> 9 ** (1/2)
3.0
5. Quotient dan remainder
Untuk menentukan hasil bagi dan sisa divisi, masing-masing menggunakan divisi lantai dan operator modulo. Pembagian lantai dilakukan dengan menggunakan dua garis miring ke depan (//). Operator modulo dijalankan dengan simbol persen (%). Operator ini dapat digunakan dengan float dan integer.
>>> 20 // 6
3
>>> 1.25 % 0.5
0.25
6. menulis kalimat dengan tanda petik.
>>> "Python is fun!"
'Python is fun!'
>>> 'Always look on the bright side of life'
'Always look on the bright side of life'
7. Tuple
Sebuah tuple adalah urutan objek yang dipisahkan oleh koma dan terlampir dalam kurung. Jika tuple berisi objek tunggal, koma akhir diperlukan; misalnya, x = (2,). Tuples mendukung operasi yang sama dengan string; mereka juga tidak berubah. Berikut adalah contoh di mana tuple rec berisi tuple lain (25,05,2000):
contohnya.
>>>rec = ("Adam", "Ilham", "Maulana", (25, 5, 2000))
>>>NamaDepan, NamaTengah, NamaAkhir, TglLahir = rec
>>>print (NamaDepan)
Adam
>>>Bulanlahir = TglLahir [1]
>>>print (Bulanlahir)
5
>>>nama = rec[1]+ ' ' + rec[2] + ' ' + rec[0]
>>>print (nama)
Ilham Maulana Adam
8. Comparison Opereators
Operator perbandingan (relasional) mengembalikan Benar atau Salah. Operator-operator ini antara lain.
>>> a = 2
>>> b = 1.99
>>> c = ’2’
>>> print(a > b)
True
>>> print(a == c)
False
>>> print((a > b) and (a != c))
True
>>> print((a > b) or (a == b))
True
Menyelesaikan tugas 1 dengan Python
1. Membuka IDLE (Python)
2. Masukan codes
1. import sympy
memasukan modul sympy
2. x = sympy.symbol('x')
mendefinisikan x sebagai symbol
3. fungsi = (x**2-1)/(x-1)
menyimpan perhitungan dalam variabel fungsi.
4. hasil = sympy.limit(fungsi, x, 1)
menyimpan hasil perhitungan dalam variabel hasil.
5. print(hasil)
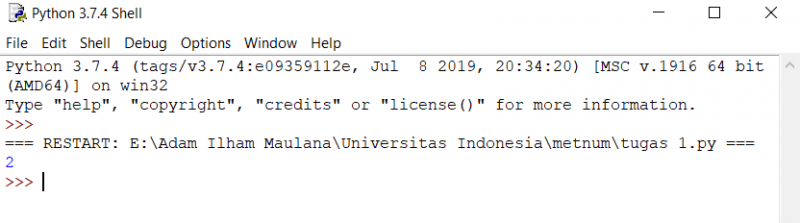
3. Press F5
hasil akan muncul.
Pertemuan Kedua
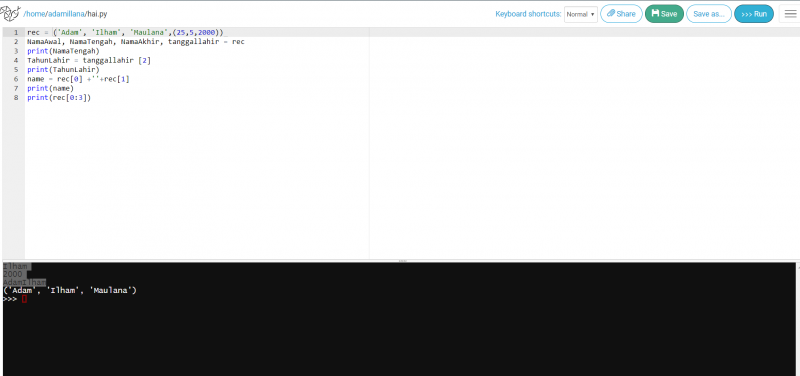
1. Cara membuat nama dan tanggal lahir
1. rec = ('Adam', 'Ilham', 'Maulana',(25,5,2000))
2. NamaAwal, NamaTengah, NamaAkhir, tanggallahir = rec
3. print(NamaTengah)
4. TahunLahir = tanggallahir [2]
5. print(TahunLahir)
6. name = rec[0] ++rec[1]
7. print(name)
5. print(rec[0:3])
Cara mengerjakan deret fibonacci dengan python
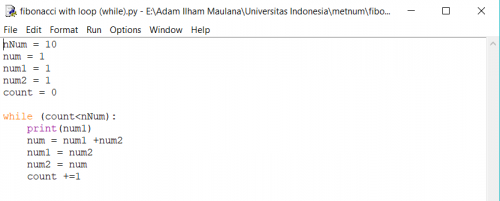
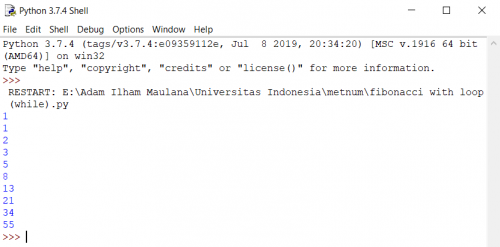
1. metode loop (while/for)
ket: untuk menetukan suku keberapa tinggal ubah nNum: (disini saya mencoba menemukan suke ke 10 untuk deret fibonacci yang dimulai dari 1)
setelah itu jalankan.
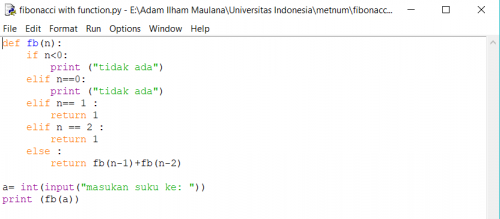
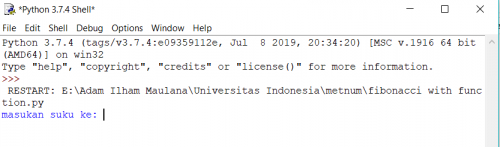
2. metode function
kemudian jalankan
setelah dijalankan kemudian tentukan suku keberapa (disini saya mencari suku ke 15)
belajar mengaplikasikan meode numerik dengan python
- numpy merupakan library yang ada di python - fungsi eval merubah string jadi number. - ni adalah jumlah node - np.zeros((ni,ni),float) membentuk matriks isinya 0 ukurannya ni*ni. - n_k adalah matriks yang isinya data data dari konstanta pegas
aplikasi differensial dengan metode numerik
terlebih dahulu kita harus membuat model sebelum melakukan komputasi dalam komputer
metode numerik dalam teknik mesin ada 3 aspek
seorang engineer adalah bagaimana caranya untuk memodelkan
lalu bagaimana caranya memodelkan suatu barang yang natinya dapat digunakan secara continu. misalnya ada sebuah benda diberikan gaya kemudian benda itu memiliki massa dan gaya itu terdistribusi ke seluruh bagian benda itu. dan itu yang dinamakan continu. melalui sifat continu dapat diterapkan beberapa hukum dalam sebuah benda contohnya, akan menghasilkan model matematis
metode runge kutta
slah satu metode untuk memnyelesaikan persamaan differensial.
Jawaban quiz
a. problem set 2.1 nomer 6 halaman 55
- Definisikan Matriks A
A = np.array([[0, 0, 2, 1, 2],
[0, 1, 0, 2, -1],
[1, 2, 0, -2, 0],
[0, 0, 0, -1, 1],
[0, 1, -1, 1, -1]], float)
- Definisikan Matriks B
b = np.array([[1],
[1],
[-4],
[-2],
[-1]],float)
Ab = np.hstack([A, b]) print (Ab, "\n")
n = len(b)
- Fase Eliminasi
for i in range(0, n-1):
for j in range(i + 1, n):
lam = Ab[i,i] / Ab[j,i]
Ab[j] = Ab[i] - lam * Ab[j]
print ("Hasil Fase Eliminasi \n", Ab, "\n")
- Fase Substitusi
for i in range(n - 1, -1, -1):
Ab[i] = Ab[i] / Ab[i, i]
for j in range(i - 1, -1, -1):
b = Ab[j]
lam = Ab[i,i] / Ab[j,i]
Ab[j] = Ab[i] - lam * Ab[j]
print ("Hasil Fase Substitusi \n", Ab, "\n")
x = Ab[:, 5]
print ("nilai xnya adalah \n", x)
cara kedua
from numpy import linalg import numpy as np
#definisikan matriks A
A1 = [0, 0, 2, 1, 2] A2 = [0, 1, 0, 2, -1] A3 = [1, 2, 0, -2, 0] A4 = [0, 0, 0, -1, 1] A5 = [0, 1, -1, 1, -1]
nmat = np.array ([A1, A2, A3, A4, A5])
#definisikan matriks B
B = np.array ([1, 1, -4, -2, -1])
#Dibawah ini adalah kode untuk memecahkan persamaan aljabar linear bertuliskan (linalg)
jawaban = linalg.solve (nmat,B) a = int(jawaban[0]) b = int(jawaban[1]) c = int(jawaban[2]) d = int(jawaban[3]) f = int(jawaban[4])
#munculkan hasil
print("X1 adalah ", a) print("X2 adalah ", b) print("X3 adalah ", c) print("X4 adalah ", d) print("X5 adalah ", f)
#maka dari cara kedua didapat matriks Xnya adalah
X1 adalah 2
X2 adalah -2
X3 adalah 1
X4 adalah 1
X5 adalah -1
b. problem nomer 2 halaman 263
# Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01.
x0 = 2
y = 1 h = 0.01 x = float(input("Masukkan nilai t: ")) if x>0 :
# dydx menyatakan persamaan awal dalam soal. # Didapat hasil x^2-4y def dydx(x, y): return (x**2-4*y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x selanjutnya
x0 = x0 + h
list.append(y)
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
kemudian akan didapatkan hasil apabila t=0.03
Masukkan nilai t: 0.03
Nilai y pada t = 0.03 adalah 1
Ujian Tengah semester
Soal nomer satu
Input
- -*- coding: utf-8 -*-
""" Created on Wed Oct 23 13:30:54 2019
@author: Adam Ilham Maulana """
#Bismillahirrahmanirrahim
#soal nomer 1. carilah tegangan tali.
import math
#Tentukan variabel-variabel yang akan digunakan dalam perhitungan
g=9.81
M1=eval(input("besar massa benda 1 ?")) #masukkan 30 kg
M2=eval(input("besar massa benda 2 ?")) #masukkan 20 kg
M3=eval(input("besar massa benda 3 ?")) #masukkan 10 kg
k1=eval(input("Koefisien gesek benda 1 ?")) #masukkan 0.6
k2=eval(input("koefisien gesek benda 2 ?")) #masukkan 0.4
k3=eval(input("Koefisien gesek benda 3 ?")) #masukkan 0.2
alfa=eval(input("sudutnya kemiringan ?")) #masukkan 60
a=eval(input("percepatan :")) #masukkan 5 m/s^2
x= math.sin(alfa)
y= math.cos(alfa)
#buat rumus untuk mencari Tegangan tali 1, 2, dan 3
T1=M1*g*(x-k1*y)-M1*a
T2=M2*g*(x-k2*y)+T1-M2*a
T3=M3*g*(x-k3*y)+T2-M3*a
#akan didapatkan hasilnya
print ("tegangan tali T1 adalah", abs(T1))
print ("tegangan tali T2 adalah", abs(T2))
print ("tegangan Tali T2 adalah", abs(T3))
output
runfile('E:/Adam Ilham Maulana/Universitas Indonesia/metnum/untitled3.py', wdir='E:/Adam Ilham Maulana/Universitas Indonesia/metnum')
besar massa benda 1 ? 30
besar massa benda 2 ? 20
besar massa benda 3 ? 10
Koefisien gesek benda 1 ? 0.6
koefisien gesek benda 2 ? 0.4
Koefisien gesek benda 3 ? 0.2
sudutnya kemiringan ? 60
percepatan : 5
dapat hasilnya
tegangan tali T1 adalah 71.52868170867406
tegangan tali T2 adalah 156.5871548659475
tegangan Tali T2 adalah 217.80273412032957
soal nomer 2
#definisikan variabel-variabel yang akan digunakan
g = 9.81
densitas = 1.2 #merupakan massa jenis udara
cd = eval(input("koefisien drag:"))
area = eval(input("luas (m^2):"))
v1 = eval(input("kecepatan yang diinginkan:"))
m = eval(input("massa mobil(kg):"))
u = eval(input("koefisien gesek:"))
a = eval(input("percepatan(m/s^2):"))
#cari percepatan yang disebabkan gaya gesek (ag) dan yang disebabkan oleh gaya hambat udara (adrag)
ag = g*u
for v0 in range (0,v1):
adrag = (cd*area*densitas*v0**2)/2*m
atot = a - (adrag + ag) #berasal dari rumus Ftot/massa total
#masukkan rumus untuk mendapatkan waktu yg diperlukan
t = -(v1)/atot
- kemudian didapatkan waktu yang diperlukan untuk mencapai kecepatan tertentu
print("waktu yang diperlukan untuk mencapai kecepatan yang diinginkan:", t, "sekon")
Contoh Soal Runge kutta
intro
Rasulullah SAW. menganjurkan umat muslim untuk memanah. kemudian beliau bersabda.
“Sesungguhnya ia mengatakan, “Barangsiapa telah mengetahui tentang memanah kemudian meninggalkannya, maka dia bukan termasuk golonganku, atau telah bermaksiat.” (HR. Muslim)
soal
sebuah anak panah dilontarkan dari keadaan diam, dengan massa 0.2 kg. dan kaliber 3 cm dan diketahuai gaya koefisien drag dari udara sebesar 0.1 dan memiliki percepatan. diketahuai F sebesar 800t N pada saat 0=<t<0.5 dan F sebesar 800 pada saat t>=0.5
tentukan kecepatan laju anak panah pada saat anak panah tersebut pada waktu 2 s!!
penyelesaian dengan rumus rungue kutta
# -*- coding: utf-8 -*-
""" Created on Wed Nov 6 15:08:38 2019
@author: USER """
#pendefinisian soal # t0 dan v0 sebagai keadaan awal, t sebagai t yang diinput, dan h sebagai increment
t0 = 0 v0 = 0 h = 0.01 # di sini digunakan h = 0.01 t = float(input("masukkan nilai t: ")) # perintah untuk memasukkan nilai t
if 0 <= t < 0.5: # untuk 0 <= t < 0.2
def F(t, v):
return (4000 * t - 0.0001125 * (v**2)) # persamaan a yang diperoleh dari soal.
#metode runge kutta
def rungeKutta(t0, v0, t, h):
n = (int)((t - t0) / h)
v = v0
for i in range(1, n + 1):
k1 = h * F(t0, v)
k2 = h * F(t0 + 0.5 * h, v + 0.5 * k1)
k3 = h * F(t0 + 0.5 * h, v + 0.5 * k2)
k4 = h * F(t0 + h, v + k3)
v = v + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
t0 = t0 + h
return v
print("Nilai v pada t =", t, "adalah", rungeKutta(t0, v0, t, h), "m/s") # nilai v akan muncul sesuai dengan t yang dimasukkan
elif t >= 0.1: # untuk t >= 0.1
def F(t, v):
return (4000 - 0.0001125 * (v**2)) # persamaan a yang telah diperoleh
def rungeKutta(t0, v0, t, h): # perhitungan Runge-Kutta
n = (int)((t - t0) / h)
v = v0
for i in range(1, n + 1):
k1 = h * F(t0, v)
k2 = h * F(t0 + 0.5 * h, v + 0.5 * k1)
k3 = h * F(t0 + 0.5 * h, v + 0.5 * k2)
k4 = h * F(t0 + h, v + k3)
v = v + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
t0 = t0 + h
return v
print("Nilai v pada t =", t, "adalah", rungeKutta(t0, v0, t, h), "m/s") # nilai v akan muncul sesuai dengan nilai t yang dimasukkan
else:
print("Nilai t harus positif.")
Curve fitting
curve fitting dibagi jadi dua
- regresi.
konsep yangpaling m,udah adalah regresi linear. garis yang mendekati adalah yang memiliki error paling kecil.
- interpolasi
Optimasi
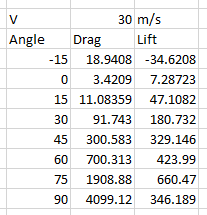
Untuk tugas ini, kami menggunakan referensi airfoil NACA-0009 9.0% smoothed untuk mendapatkan nilai drag force dan lift force pada kecepatan 30 m/s
Variabel pada tugas ini adalah angle airfoil dari -15° hingga 90°
dengan bantuan aplikasi CFDSOF dan Paraview
didapatkan nilai-nilai sebagai berikut
Grafik Drag
Grafik Lift
Hasil Optimasi
import numpy as np
from scipy.optimize import minimize
def drag(x):#drag
x = x[0]
d = 0.0001*x**4 -0.0049*x**3 + 0.1194*x**2 - 1.38*x - 6.927
return d
def lift(x): #lift
x = x[0]
l = -0.00006*x**4 + 0.0066*x**3 - 0.0652*x**2 + 1.7418*x + 24.193
return l
def obj(x): #sudut yang diminimalkan
return drag(x)
def c1(x): #variable SUDUT yang meminimalkan persamaan garis drag
return drag(x)
def c2(x): #variable SUDUT yang meminimalkan persamaan garis lift
return lift(x)
con1=({'type':'ineq','fun':c1})
con2=({'type':'ineq','fun':c2})
cons = (con1,con2)
a = (10,90)
batas = [a]
x1_guess = 20
x0 = np.array([x1_guess])
sol = minimize(obj,x0, method='SLSQP', bounds=batas, constraints=cons, options={'disp':True})
xopt = sol.x
fopt = -sol.fun
dopt = drag(xopt) # drag optimal
lopt = lift(xopt) # lift optimal
print ('sudut optimal = '+str(xopt[0]), "\n", 'total force optimal = '+str(fopt), "\n", 'drag force optimal = '+str(-dopt), "\n", 'lift force optimal = '+str(lopt))
Aplikasi ANN pada Data CFD
Koding ANN (Dengan Google Colab)
import tensorflow as tf from tensorflow import keras from tensorflow.keras import Sequential from tensorflow.keras.layers import Flatten, Dense import numpy as np import pandas as pd print(tf.__version__) from google.colab import files uploaded = files.upload() import io database = pd.read_excel(io.BytesIO(uploaded['ANN ELVIN.xlsx'])) x = database['angle of attack'] #y1 = dataset['Fdrag'] #y2 = dataset['Flift'] y = database['drag/lift'] import matplotlib.pyplot as plt plt.plot(x,y)
norm_x = [(a-np.min(x))/(np.max(x)-np.min(x))
for a in x]
norm_y = [(a-np.min(y))/(np.max(y)-np.min(y))
for a in y]
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(norm_x, norm_y, test_size = 0.3, random_state =
0)
x_train = np.asarray(x_train)
x_test = np.asarray (x_test)
y_train = np.asarray (y_train)
y_test = np.asarray (y_test)
import matplotlib.pyplot as plt
unnorm_y_awal= [a*(np.max(y)-np.min(y))+np.min(y)
for a in y_test]
plt.suptitle('Output Real')
plt.plot(unnorm_y_awal)
model = Sequential()
model.add(Dense(3, activation='relu', input_dim = 1)) # input layer
model.add(Dense(4, activation='relu')) # hidden layer
model.add(Dense(1, activation = 'sigmoid'))
model.compile(optimizer='adam', loss = 'binary_crossentropy', metrics=['accuracy'])
history = model.fit(x_train, y_train, batch_size = 64, epochs = 5, verbose = 1, validation_split = 0.16)
Train on 3 samples, validate on 1 samples
Epoch 1/5
3/3 [==============================] - 0s 34ms/sample - loss: 0.7800 - acc: 0.0000e+00 - val_loss: 0.8347 - val_acc: 0.0000e+00
Epoch 2/5
3/3 [==============================] - 0s 2ms/sample - loss: 0.7782 - acc: 0.0000e+00 - val_loss: 0.8323 - val_acc: 0.0000e+00
Epoch 3/5
3/3 [==============================] - 0s 1ms/sample - loss: 0.7765 - acc: 0.0000e+00 - val_loss: 0.8299 - val_acc: 0.0000e+00
Epoch 4/5
3/3 [==============================] - 0s 1ms/sample - loss: 0.7748 - acc: 0.0000e+00 - val_loss: 0.8275 - val_acc: 0.0000e+00
Epoch 5/5
3/3 [==============================] - 0s 2ms/sample - loss: 0.7731 - acc: 0.0000e+00 - val_loss: 0.8252 - val_acc: 0.0000e+00
unnorm_x= [a*(np.max(x)-np.min(x))+np.min(x)
for a in x_test]
unnorm_y= [a*(np.max(y)-np.min(y))+np.min(y)
for a in y_test]
plt.suptitle('Output Real vs Output Prediction ANN')
plt.subplot(2, 1, 1)
plt.plot(unnorm_y_awal)
plt.subplot(2, 1, 2)
plt.plot(unnorm_y)
Hasil
Dapat dilihat bahwa output real dengan output prediction ANN sama persis