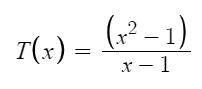Difference between revisions of "AZ"
m (Anggitoz moved page Muhammad Anggito Zhafranny to AZ: hide personal information) |
|||
| (40 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
== Profile == | == Profile == | ||
| − | |||
| − | |||
| + | |||
| + | |||
| + | |||
| + | ==Core Python== | ||
| + | |||
| + | ====Numpy, SciPy, and Matplotlib==== | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | (work) C:\DEV>python -m pip install numpy | ||
| + | (work) C:\DEV>python -m pip install scipy | ||
| + | (work) C:\DEV>python -m pip install matplotlib | ||
| + | </div> | ||
| + | |||
| + | ''''Numpy'''' is the core library for scientific computing in Python. It provides a high-performance multidimensional array object, and tools for working with these arrays. If you are already familiar with MATLAB, you might find this tutorial useful to get started with Numpy. Numpy provides a high-performance multidimensional array and basic tools to compute with and manipulate these arrays. ''''SciPy'''' builds on this, and provides a large number of functions that operate on numpy arrays and are useful for different types of scientific and engineering applications. | ||
| + | |||
| + | ''''Matplotlib'''' is a plotting library. In this section give a brief introduction to the matplotlib.pyplot module, which provides a plotting system similar to that of MATLAB. | ||
| + | |||
| + | Then click enter and appeared to be like this: | ||
| + | |||
| + | [[File:Installing numpy scipy and matplotlib.jpg|500px]] | ||
| + | |||
| + | ===Python Tutorial=== | ||
| + | |||
| + | Link [http://cs231n.github.io/python-numpy-tutorial/#python Click Here] and click https://en.wikibooks.org/wiki/Python_Programming/Basic_Math | ||
| + | also from here learnpython.org | ||
| + | |||
| + | == Numerical Methods == | ||
| + | |||
| + | This section serves as my study journal of Numerical Methods through my Fifth Semester at DTM UI. | ||
| + | |||
| + | ===1st Session=== | ||
| + | |||
| + | Lecturer : Dr. Ahmad Indra and Dr. Ir. Engkos Kosasih | ||
| + | |||
| + | Date : 02 September 2019 | ||
| + | |||
| + | ﷽ | ||
| + | |||
| + | '''Introduction''' | ||
| + | |||
| + | Class is being held at Class GK201. A Computer Laboratory. The class was supposed being held by Mr. Achmad Riadi and Dr. Ir. Engkos A. Kosasih yet suprising moments happen when Dr. Ahmad Indra Siswantara or Pak DAI appearing instead. Pak Engkos appeared after a half hour. | ||
| + | |||
| + | At the beginning, Pak DAI told us the essence of praying before studying, the meaning of our purpose of studying and also the difference of us, engineers and accountant at viewing measurement tolerance before and then we continue to introduction of Numerical Methods. An accountant and economist would see measurement down to every detail like how they counting country's debt down to double digit cent while we engineers are so tolerant at measurements as long as it does not create trouble or mishaps at designed machine or system. | ||
| + | |||
| + | According to Pak Engkos, Numerical Method is simply how to using algorythim and equation we learn from prior subject we learn (ex. Engineering Mathematics) and how to communicate or speak language of computer in order to achieve the results of process a large equation that might be impossible to calculated by human minds alone. Any equations that can be completed with numerics can also be attained by exact way but not vice versa. Human might can calculate first or second order, but in higher order we need to use engineering computation to attain results efficiently and quicker. It's is not something we can calculated with paper in higher order, said Pak Engkos. | ||
| + | |||
| + | Tools of Numerical Methods: Python, C++, Java, etc. | ||
| + | Any computation language is eligible to use said Pak DAI and seems picking using python as tools. | ||
| + | |||
| + | ===2nd Session=== | ||
| + | |||
| + | Lecturer : Dr. Ahmad Indra Siswantara | ||
| + | |||
| + | Date : 09 September 2019 | ||
| + | |||
| + | '''Iterative Method''' | ||
| + | |||
| + | There is no term of Common Sense, rather any sense or mind is right and the wrong ones is our intrigue, temptation, and sort off... | ||
| + | <br>- Pak DAI | ||
| + | |||
| + | ''The Iterative Method'' is a mathematical way of solving a problem which generates a sequence of approximations. This method is applicable for both linear and nonlinear problems with large number of variables. | ||
| + | |||
| + | [[File:29244.png]] | ||
| + | |||
| + | mengapa hasilnya 2 tidak 0/0? | ||
| + | |||
| + | Angka bulat itu tidak ada. | ||
| + | |||
| + | TL;DR | ||
| + | * ''0/0 tidak konsisten'' karena jika persamaan ini dihadapkan dengan beberapa kasus atau argumen maka bisa didapatkan berbeda hasil, padahal jika dalam eksakta, aturannya adalah hasil persamaan tidak bisa diubah, pasti atau bisa disamakan dengan absolut. | ||
| + | ada beberapa aturan yang kita tahu dari persamaan dengan 0 dan bilangan bulat: | ||
| + | * Jika (a/0)=infinit, jika a=0 maka 0/0=infinit | ||
| + | * Jika (0/b)=0, jika b=0 maka 0/0=0 | ||
| + | * Jika (c/c)=1, jika c=0 maka 0/0=1 | ||
| + | |||
| + | Bisa kita bandingkan dan simpulkan bahwa 0/0 tidak konsisten atau undefined/ | ||
| + | |||
| + | '''New Terms''' | ||
| + | |||
| + | * '''''Perhitungan komputasi''''' undefined/tidak konsisten/error cannot appeared on computer. | ||
| + | |||
| + | * '''''Discrete >< Continous''''' | ||
| + | |||
| + | : > '''''Discrete''''' can only take certain values. Not Decimal. | ||
| + | |||
| + | : > '''''Continous''''' can take any value (within a range). | ||
| + | |||
| + | * '''''Algoritma''''' is an arrangement of instructions to solve problems. | ||
| + | |||
| + | * '''''Flowchart''''' a diagram that uses a set of standard graphic symbols to represent the sequence of coded instructions fed into a computer, enabling it to perform specified logical and arithmetical operations. | ||
| + | |||
| + | * '''''Program''''' consists of compiled code that can run directly from the computer's operating system. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''PR / Hiburan I''' | ||
| + | |||
| + | Cari x di persamaan berikut menggunakan peranti lunak Python | ||
| + | <Br>[[File:80092.png]] | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | [[file:1568599528431.jpg|thumb|550px|Results]] | ||
| + | def f(x): | ||
| + | return 8*x**3 + 2*x**2 + x - 1 | ||
| + | def fprime(x): | ||
| + | return 24*x**2 + 4*x +1 | ||
| + | <br>ep = 0.001 | ||
| + | <br>gu = -10 | ||
| + | i = 0 | ||
| + | <br>print('8*x**3 + 2*x**2 + x - 1') | ||
| + | <br>print('Results by Python 3.7') | ||
| + | <br>while abs(f(gu)) >= ep: | ||
| + | gu = gu - (f(gu)/fprime(gu)) | ||
| + | i += 1 | ||
| + | print(' ' + str(i) + ' ' + str(round(gu,7))) | ||
| + | <br>print('The root approach is ' + str(round(gu,2)) + | ||
| + | '| failed to calculate: ' + str(i) + ' times' ) | ||
| + | </div> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ===3rd Session=== | ||
| + | |||
| + | Missed 3rd Session | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ===4th Session=== | ||
| + | |||
| + | Lecturer : Dr. Ahmad Indra and assistant Edo | ||
| + | |||
| + | Date : 23 September 2019 | ||
| + | |||
| + | '''Systems of Linear Algebraic Equations''' | ||
| + | |||
| + | '''Pr / Hiburan II''' | ||
| + | |||
| + | [[File:PR_sesi_4.jpg]] | ||
| + | |||
| + | Convert to array/matrix equation in order to eliminate it using Gaussian Elimination. Thus its equation and matrix are: | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | 6x<sub>1</sub> - 4x<sub>2</sub> = 50 | ||
| + | -2x<sub>1</sub> - x<sub>3</sub> + 4x<sub>4</sub> = 50 | ||
| + | -7x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> = 0 | ||
| + | 4x<sub>1</sub> - 4x<sub>3</sub> = 0 | ||
| + | |||
| + | Therefore resulting this in matrix | ||
| + | [[ 6. -4. 0. 0.] | ||
| + | [-2. 0. -1. 4.] | ||
| + | [ 0. -7. 3. 4.] | ||
| + | [ 4. 0. -4. 0.]] | ||
| + | </div> | ||
| + | |||
| + | Then define those matrix in python. | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | import numpy as np | ||
| + | <br>A = np.array([[6, -4, 0, 0], [-2, 0 ,-1, 4], [0, -7, 3, 4], [ 4, 0, -4, 0]], float) | ||
| + | B = np.array([50, 50, 0, 0], float) | ||
| + | <br>n = len(A) | ||
| + | </div> | ||
| + | |||
| + | '''Use Gaussian Elimination''' | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | for k in range(0,n-1): | ||
| + | for i in range(k+1,n): | ||
| + | if A[i,k]!=0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) | ||
| + | B[i] = B[i]-(B[k]*lam) | ||
| + | </div> | ||
| + | |||
| + | '''Back Subtitution''' | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | x = np.zeros(n,float) | ||
| + | for m in range(n-1,-1,-1): | ||
| + | x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m] | ||
| + | </div> | ||
| + | |||
| + | '''Results''' | ||
| + | |||
| + | [[File:13124141431.png|500px]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ===5th Session=== | ||
| + | |||
| + | Lecturer : Dr. Ahmad Indra | ||
| + | |||
| + | Date : 30 September 2019 | ||
| + | |||
| + | ''' | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ===6th Session=== | ||
| + | |||
| + | Lecturer : Dr. Ahmad Indra | ||
| + | |||
| + | Date : 7 Oktober 2019 | ||
| + | |||
| + | '''Runge-Kutta Method''' | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ===7th Session - QUIZ=== | ||
| + | |||
| + | ====QUIZ 01==== | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | import numpy as np | ||
| + | A=np.array([[1., 2., 0., -2., 0.], | ||
| + | [0., 1., 0., 2., -1.], | ||
| + | [0., 0., 2., 1., 2.], | ||
| + | [0., 0., 0., -1., 1.], | ||
| + | [0., 1., -1., 1., -1.]], float) | ||
| + | B=np.array([1, 1, -4, -2, -1], float) | ||
| + | <br>n = len(A) | ||
| + | <br>print('Matriks A adalah:') | ||
| + | print(A,'\n') | ||
| + | print('Matriks A memiliki ', n , ' baris','\n') | ||
| + | print('Matriks B adalah:') | ||
| + | print(B,'\n') | ||
| + | for k in range(0,n-1): | ||
| + | for i in range(k+1,n): | ||
| + | if A[i,k]!=0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) | ||
| + | B[i] = B[i]-(B[k]*lam) | ||
| + | print('matrix A:', '\n', A) | ||
| + | print('Nilai x masing-masing adalah:') | ||
| + | x = np.zeros(n,float) | ||
| + | for m in range(n-1,-1,-1): | ||
| + | x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m] | ||
| + | print('C',m+1,'=', x[m]) | ||
| + | |||
| + | </div> | ||
| + | |||
| + | [[File:Quiz01 no 1.jpg|500px]] | ||
| + | |||
| + | ====QUIZ 02==== | ||
| + | |||
| + | Menggunakan modul printSoln dan '''run_kut4''' | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | import numpy as np | ||
| + | def integrate(F,x,y,xStop,h): | ||
| + | def run_kut4(F,x,y,xStop,h): | ||
| + | K0 = h*F(x,y) | ||
| + | K1 = h*F(x+h/2, y+K0/2) | ||
| + | K2 = h*F(x+h/2, y+K1/2) | ||
| + | K3 = h*F(x+h,y+K2) | ||
| + | return (K0+2*K1+2*K2+K3)/6 | ||
| + | X = [] | ||
| + | Y = [] | ||
| + | X.append(x) | ||
| + | Y.append(y) | ||
| + | while x < xStop: | ||
| + | h = min(h,xStop - x) | ||
| + | y = y + run_kut4(F,x,y,xStop,h) | ||
| + | x = x+h | ||
| + | X.append(x) | ||
| + | Y.append(y) | ||
| + | return np.array(X),np.array(Y) | ||
| + | |||
| + | '''Quiz no.2 | ||
| + | <div border-style: inset;"> | ||
| + | #!/usr/bin/python | ||
| + | ## example7_5 | ||
| + | import numpy as np | ||
| + | from run_kut4 import * | ||
| + | from printSoln import * | ||
| + | from math import exp<Br> | ||
| + | x = 0.03 | ||
| + | def F(x,y): | ||
| + | F = np.zeros(1) | ||
| + | F[0] = ((31/32)*exp(-4))+((1/4)*x**2)-(1/8)*x+(1/32) | ||
| + | return F<Br> | ||
| + | x = 0.0 <span style="color:#ff0000"># Start of integration</span> | ||
| + | xStop = 0.03 <span style="color:#ff0000"># End of integration</span> | ||
| + | y = np.array([1]) <span style="color:#ff0000"># Initial values of {y}</span> | ||
| + | h = 0.01 <span style="color:#ff0000"># Step size</span> | ||
| + | freq = 1 <span style="color:#ff0000"># Printout frequency</span><Br> | ||
| + | print(y)<Br> | ||
| + | X,Y = integrate(F,x,y,xStop,h) | ||
| + | printSoln(X,Y,freq) | ||
| + | input("\nPress return to exit") | ||
| + | </div> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | === Ujian Tengah Semester === | ||
| + | |||
| + | ==== UTS No.1 ==== | ||
| + | |||
| + | Hasil Pengerjaan, ''Click to enlarge'' | ||
| + | |||
| + | <gallery> | ||
| + | File:Uts-toz00.jpg|Analisis dan Flowchart | ||
| + | File:Uts-toz01.jpg|Kodingan Python | ||
| + | File:Uts-toz03.jpg|Hasil Kodingan | ||
| + | </gallery> | ||
| + | |||
| + | ''Youtube'' | ||
| + | |||
| + | <youtube width="200" height="100">https://youtu.be/TdJA8fc4cZM</youtube> | ||
| + | |||
| + | ''Kodingan'' | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | import math | ||
| + | import numpy as np<Br> | ||
| + | <span style="color:#ff0000"># Define Matrices </span> | ||
| + | A = np.array([[1., 0., 0.], | ||
| + | [-1., 1., 0.], | ||
| + | [0., -1., 1.]], float) | ||
| + | B = np.array([6, 5, 4], float)<Br> | ||
| + | n = len(A)<Br> | ||
| + | <span style="color:#800080">print</span>('Matriks A adalah:') | ||
| + | <span style="color:#800080">print</span>(A,'\n') | ||
| + | <span style="color:#800080">print</span>('Matriks A memiliki ', n , ' baris','\n') | ||
| + | <span style="color:#800080">print</span>('Matriks B adalah:') | ||
| + | <span style="color:#800080">print</span>(B,'\n')<Br> | ||
| + | <span style="color:#ff0000"># Gauss Elimination </span> | ||
| + | for k in range(0,n-1): | ||
| + | for i in range(k+1,n): | ||
| + | if A[i,k]!=0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) | ||
| + | B[i] = B[i]-(B[k]*lam)<Br> | ||
| + | <span style="color:#800080">print</span>('matrix A:', '\n', A, '\n')<Br> | ||
| + | <span style="color:#ff0000"># Back Substitution </span> | ||
| + | <span style="color:#800080">print</span>('Nilai Tegangan masing-masing adalah:') | ||
| + | x = np.zeros(n,float) | ||
| + | for m in range(n-1,-1,-1): | ||
| + | x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m] | ||
| + | <span style="color:#800080">print</span>('T',m+1,'=', x[m]) | ||
| + | </div> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ==== UTS No.2 ==== | ||
| + | |||
| + | Hasil Pengerjaan, ''Click to enlarge'' | ||
| + | |||
| + | <gallery> | ||
| + | File:Uts-toz00.jpg|Analisis dan Flowchart | ||
| + | File:Uts-toz01.jpg|Kodingan Python | ||
| + | File:Uts-toz03.jpg|Hasil Kodingan | ||
| + | </gallery> | ||
| + | |||
| + | '''Youtube''' | ||
| + | |||
| + | <youtube width="200" height="100">xxxxxxxxx</youtube> | ||
| + | |||
| + | '''Kodingan''' | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | |||
| + | </div> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ==== Refleksi Diri ==== | ||
| + | |||
| + | Video ini adalah kegiatan merangkum hal yang saya dapat selama setengah semester belajar Metode Numerik bersama Dr. Ahmad Indra | ||
| + | |||
| + | <youtube width="200" height="100">https://youtu.be/_mDlvhNTi7s</youtube> | ||
== Fluid Mechanics == | == Fluid Mechanics == | ||
| Line 84: | Line 453: | ||
''Youtube'' | ''Youtube'' | ||
| − | <youtube width="200" height="100"> | + | <youtube width="200" height="100">UDRKHeWMFGA</youtube> |
| + | |||
| + | |||
| + | ==References== | ||
| + | Fluid Mechanics | ||
| + | # MUNSON, B. R., YOUNG, D. F., & OKIISHI, T. H. (2006). FUNDAMENTALS OF FLUID MECHANICS. Hoboken, NJ, J. Wiley & Sons. | ||
| + | Numerical Method | ||
| + | # [https://www.dropbox.com/s/spbsy24qm91r4v6/Jaan%20Kiusalaas-Numerical%20Methods%20in%20Engineering%20with%20Python%203-Cambridge%20University%20Press%20%282013%29.pdf?dl=0 KIUSALAAS, J. (2013). NUMERICAL METHODS IN ENGINEERING WITH PYTHON. Tribeca, NY, Cambridge University Press] | ||
Latest revision as of 20:17, 5 October 2024
THIS IS FINE This Page isn't Completed Yet the deadline is near. Help.
Profile
Core Python
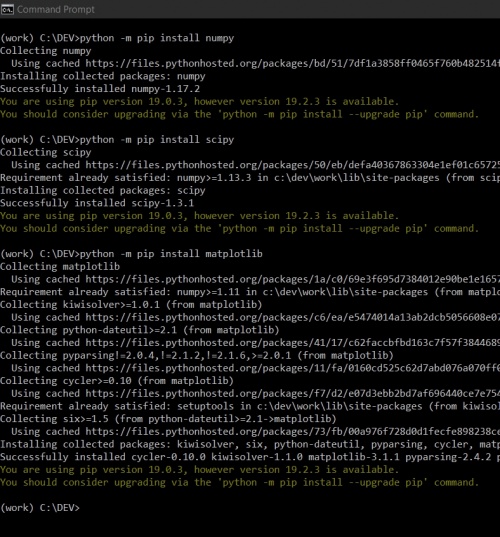
Numpy, SciPy, and Matplotlib
(work) C:\DEV>python -m pip install numpy (work) C:\DEV>python -m pip install scipy (work) C:\DEV>python -m pip install matplotlib
'Numpy' is the core library for scientific computing in Python. It provides a high-performance multidimensional array object, and tools for working with these arrays. If you are already familiar with MATLAB, you might find this tutorial useful to get started with Numpy. Numpy provides a high-performance multidimensional array and basic tools to compute with and manipulate these arrays. 'SciPy' builds on this, and provides a large number of functions that operate on numpy arrays and are useful for different types of scientific and engineering applications.
'Matplotlib' is a plotting library. In this section give a brief introduction to the matplotlib.pyplot module, which provides a plotting system similar to that of MATLAB.
Then click enter and appeared to be like this:
Python Tutorial
Link Click Here and click https://en.wikibooks.org/wiki/Python_Programming/Basic_Math also from here learnpython.org
Numerical Methods
This section serves as my study journal of Numerical Methods through my Fifth Semester at DTM UI.
1st Session
Lecturer : Dr. Ahmad Indra and Dr. Ir. Engkos Kosasih
Date : 02 September 2019
﷽
Introduction
Class is being held at Class GK201. A Computer Laboratory. The class was supposed being held by Mr. Achmad Riadi and Dr. Ir. Engkos A. Kosasih yet suprising moments happen when Dr. Ahmad Indra Siswantara or Pak DAI appearing instead. Pak Engkos appeared after a half hour.
At the beginning, Pak DAI told us the essence of praying before studying, the meaning of our purpose of studying and also the difference of us, engineers and accountant at viewing measurement tolerance before and then we continue to introduction of Numerical Methods. An accountant and economist would see measurement down to every detail like how they counting country's debt down to double digit cent while we engineers are so tolerant at measurements as long as it does not create trouble or mishaps at designed machine or system.
According to Pak Engkos, Numerical Method is simply how to using algorythim and equation we learn from prior subject we learn (ex. Engineering Mathematics) and how to communicate or speak language of computer in order to achieve the results of process a large equation that might be impossible to calculated by human minds alone. Any equations that can be completed with numerics can also be attained by exact way but not vice versa. Human might can calculate first or second order, but in higher order we need to use engineering computation to attain results efficiently and quicker. It's is not something we can calculated with paper in higher order, said Pak Engkos.
Tools of Numerical Methods: Python, C++, Java, etc. Any computation language is eligible to use said Pak DAI and seems picking using python as tools.
2nd Session
Lecturer : Dr. Ahmad Indra Siswantara
Date : 09 September 2019
Iterative Method
There is no term of Common Sense, rather any sense or mind is right and the wrong ones is our intrigue, temptation, and sort off...
- Pak DAI
The Iterative Method is a mathematical way of solving a problem which generates a sequence of approximations. This method is applicable for both linear and nonlinear problems with large number of variables.
mengapa hasilnya 2 tidak 0/0?
Angka bulat itu tidak ada.
TL;DR
- 0/0 tidak konsisten karena jika persamaan ini dihadapkan dengan beberapa kasus atau argumen maka bisa didapatkan berbeda hasil, padahal jika dalam eksakta, aturannya adalah hasil persamaan tidak bisa diubah, pasti atau bisa disamakan dengan absolut.
ada beberapa aturan yang kita tahu dari persamaan dengan 0 dan bilangan bulat:
- Jika (a/0)=infinit, jika a=0 maka 0/0=infinit
- Jika (0/b)=0, jika b=0 maka 0/0=0
- Jika (c/c)=1, jika c=0 maka 0/0=1
Bisa kita bandingkan dan simpulkan bahwa 0/0 tidak konsisten atau undefined/
New Terms
- Perhitungan komputasi undefined/tidak konsisten/error cannot appeared on computer.
- Discrete >< Continous
- > Discrete can only take certain values. Not Decimal.
- > Continous can take any value (within a range).
- Algoritma is an arrangement of instructions to solve problems.
- Flowchart a diagram that uses a set of standard graphic symbols to represent the sequence of coded instructions fed into a computer, enabling it to perform specified logical and arithmetical operations.
- Program consists of compiled code that can run directly from the computer's operating system.
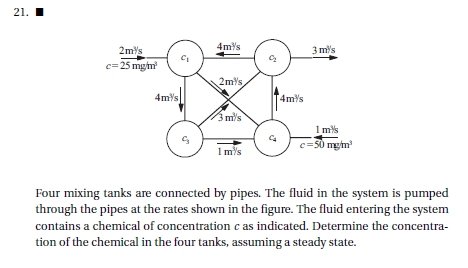
PR / Hiburan I
Cari x di persamaan berikut menggunakan peranti lunak Python
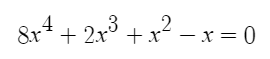
def f(x): return 8*x**3 + 2*x**2 + x - 1 def fprime(x): return 24*x**2 + 4*x +1
ep = 0.001
gu = -10 i = 0
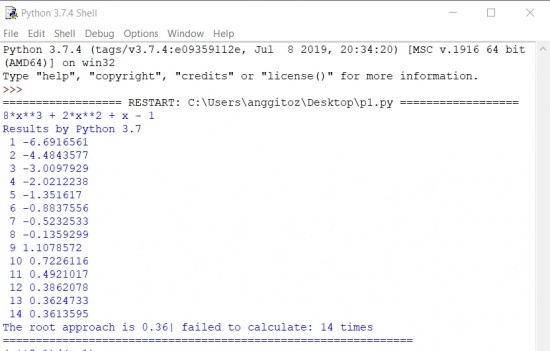
print('8*x**3 + 2*x**2 + x - 1')
print('Results by Python 3.7')
while abs(f(gu)) >= ep: gu = gu - (f(gu)/fprime(gu)) i += 1 print(' ' + str(i) + ' ' + str(round(gu,7)))
print('The root approach is ' + str(round(gu,2)) + '| failed to calculate: ' + str(i) + ' times' )
3rd Session
Missed 3rd Session
4th Session
Lecturer : Dr. Ahmad Indra and assistant Edo
Date : 23 September 2019
Systems of Linear Algebraic Equations
Pr / Hiburan II
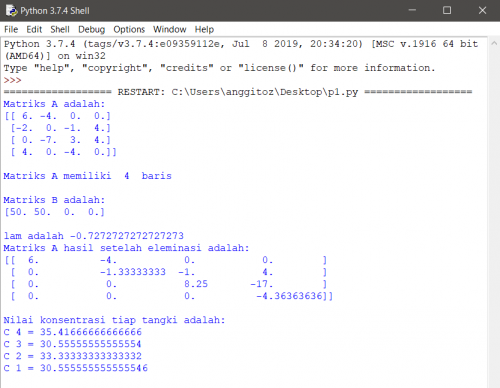
Convert to array/matrix equation in order to eliminate it using Gaussian Elimination. Thus its equation and matrix are:
6x1 - 4x2 = 50 -2x1 - x3 + 4x4 = 50 -7x2 + 3x3 + 4x4 = 0 4x1 - 4x3 = 0
Therefore resulting this in matrix
[[ 6. -4. 0. 0.] [-2. 0. -1. 4.] [ 0. -7. 3. 4.] [ 4. 0. -4. 0.]]
Then define those matrix in python.
import numpy as np
A = np.array([[6, -4, 0, 0], [-2, 0 ,-1, 4], [0, -7, 3, 4], [ 4, 0, -4, 0]], float) B = np.array([50, 50, 0, 0], float)
n = len(A)
Use Gaussian Elimination
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
Back Subtitution
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
Results
5th Session
Lecturer : Dr. Ahmad Indra
Date : 30 September 2019
6th Session
Lecturer : Dr. Ahmad Indra
Date : 7 Oktober 2019
Runge-Kutta Method
7th Session - QUIZ
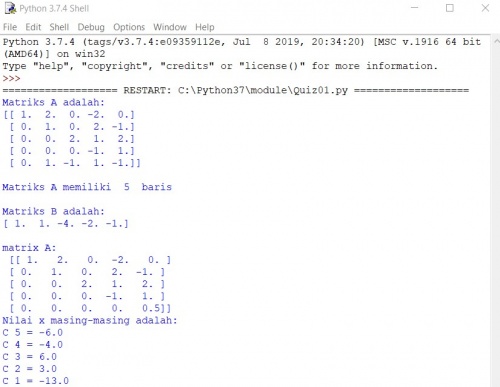
QUIZ 01
import numpy as np
A=np.array([[1., 2., 0., -2., 0.],
[0., 1., 0., 2., -1.],
[0., 0., 2., 1., 2.],
[0., 0., 0., -1., 1.],
[0., 1., -1., 1., -1.]], float)
B=np.array([1, 1, -4, -2, -1], float)
n = len(A)
print('Matriks A adalah:')
print(A,'\n')
print('Matriks A memiliki ', n , ' baris','\n')
print('Matriks B adalah:')
print(B,'\n')
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
print('matrix A:', '\n', A)
print('Nilai x masing-masing adalah:')
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
print('C',m+1,'=', x[m])
QUIZ 02
Menggunakan modul printSoln dan run_kut4
import numpy as np
def integrate(F,x,y,xStop,h):
def run_kut4(F,x,y,xStop,h):
K0 = h*F(x,y)
K1 = h*F(x+h/2, y+K0/2)
K2 = h*F(x+h/2, y+K1/2)
K3 = h*F(x+h,y+K2)
return (K0+2*K1+2*K2+K3)/6
X = []
Y = []
X.append(x)
Y.append(y)
while x < xStop:
h = min(h,xStop - x)
y = y + run_kut4(F,x,y,xStop,h)
x = x+h
X.append(x)
Y.append(y)
return np.array(X),np.array(Y)
Quiz no.2
#!/usr/bin/python ## example7_5 import numpy as np from run_kut4 import * from printSoln import * from math import exp
x = 0.03 def F(x,y): F = np.zeros(1) F[0] = ((31/32)*exp(-4))+((1/4)*x**2)-(1/8)*x+(1/32) return F
x = 0.0 # Start of integration xStop = 0.03 # End of integration y = np.array([1]) # Initial values of {y} h = 0.01 # Step size freq = 1 # Printout frequency
print(y)
X,Y = integrate(F,x,y,xStop,h) printSoln(X,Y,freq) input("\nPress return to exit")
Ujian Tengah Semester
UTS No.1
Hasil Pengerjaan, Click to enlarge
Youtube
Kodingan
import math import numpy as np
# Define Matrices A = np.array([[1., 0., 0.], [-1., 1., 0.], [0., -1., 1.]], float) B = np.array([6, 5, 4], float)
n = len(A)
print('Matriks A adalah:') print(A,'\n') print('Matriks A memiliki ', n , ' baris','\n') print('Matriks B adalah:') print(B,'\n')
# Gauss Elimination for k in range(0,n-1): for i in range(k+1,n): if A[i,k]!=0 : lam = A[i,k]/A[k,k] A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) B[i] = B[i]-(B[k]*lam)
print('matrix A:', '\n', A, '\n')
# Back Substitution print('Nilai Tegangan masing-masing adalah:') x = np.zeros(n,float) for m in range(n-1,-1,-1): x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m] print('T',m+1,'=', x[m])
UTS No.2
Hasil Pengerjaan, Click to enlarge
Youtube
Kodingan
Refleksi Diri
Video ini adalah kegiatan merangkum hal yang saya dapat selama setengah semester belajar Metode Numerik bersama Dr. Ahmad Indra
Fluid Mechanics
Here lies my case studies that examine a set of problems from textbook Fundamentals of Fluid Mechanics by Munson; Young; Okiishi; and Huebsch. I upload it in form of my handwriting on folio paper, youtube videos and text. Mainly text in Indonesian, i supposed. Mainly created as Mr. DAI instructed it to us as homework. Hope this helps your studies; Tschuss
Chapter 8: Viscous Flowin Pipes
Summary & Study Case on Folio Click to enlarge.
Chapter ini membahas tentang karakteristik aliran didalam pipa. Perpindahan energi terjadi akibat terjadi perubahan pressure atau tekanan seiring perpindahan dari titik A ke titik B.
- Toz Bab8 01.jpg
Page 1
- Toz Bab8 02.jpg
Page 2
- Toz Bab8 03.jpg
Page 3
Youtube
Chapter 9: Flow Over Immersed Bodies
Summary & Study Case on Folio Click to enlarge.
Chapter ini membahas tentang karakteristik aliran luar yang melewati benda terendam. Contoh terdekatnya adalah Ikan yang berenang didalam air. Aliran luar juga sering disebut aerodinamika. Ilmu ini diaplikasikan dalam mendesain transportasi pesawat terbang, mobil, maupun kapal selam dengan memperhatikan gaya fluida (Lift-Drag) dan Lapisan Batas suatu aliran akibat benda yang terendam.
Youtube
Chapter 10: Open-Channel Flow
Summary & Study Case on Folio Click to enlarge.
Berbeda dengan Bab 8, Bab 10 ini melibatkan aliran-aliran yang mengalir dalam kanal dan pipa yang tidak terisi sepenuhnya. Contoh aslinya adalah sungai yang berada disekeliling kita, tetapi itu masih tergolong rumit karena memerlukan pengukuran geometri dari sungai tersebut. Perbedaan signifikan antara bab 8 dan bab 10 terletak pada perubahan tekanan sebagai penggeraknya. Open-Channel Flow tidak memiliki perubahan tekanan sebagai penggerak melainkan kemiringan atau gradien dasar kanal sebagai penggerak.
Important Equation
Youtube
Chapter 11: Compressible Flow
Summary & Study Case on Folio Click to enlarge.
Membahas tentang aliran mampu-mampat yang pada dasarnya jika menyertakan persamaan kontinuitas massa, maka densitas juga ikut berubah seiring perpindahannya melewati duct konvergen-divergen atau sebaliknya. Mempelajari karakteristik aliran jika memasuki duct, dalam arti laju dll.
- Toz Bab11 01.jpg
Page 1
- Toz Bab11 02.jpg
Page 2
- Toz Bab11 03.jpg
Page 3
Youtube
References
Fluid Mechanics
- MUNSON, B. R., YOUNG, D. F., & OKIISHI, T. H. (2006). FUNDAMENTALS OF FLUID MECHANICS. Hoboken, NJ, J. Wiley & Sons.
Numerical Method