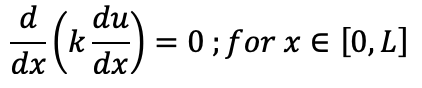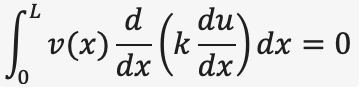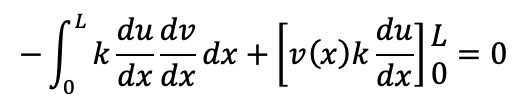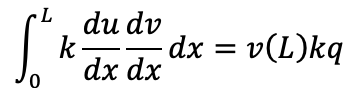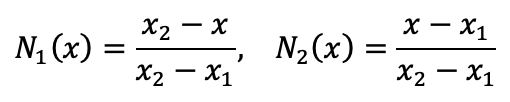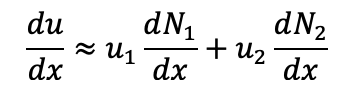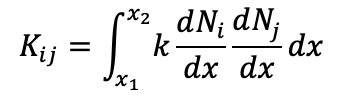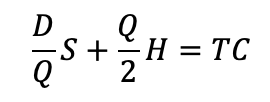Difference between revisions of "User:Muhamad.akbar41"
| (39 intermediate revisions by the same user not shown) | |||
| Line 109: | Line 109: | ||
• U is the vector of unknown nodal values, | • U is the vector of unknown nodal values, | ||
• F is the force vector, which includes contributions from the Neumann boundary condition. | • F is the force vector, which includes contributions from the Neumann boundary condition. | ||
| + | |||
| + | |||
| + | == JILID 2 : Pembuatan Kode Python == | ||
| + | |||
| + | |||
| + | '''Question 3''': Can you provide with algorithm, flow chart and python code? | ||
| + | |||
| + | Certainly! Here’s how you can implement the finite element method (FEM) for a 1D heat conduction problem step-by-step, including the algorithm, flowchart, and a sample Python code. | ||
| + | |||
| + | ### Algorithm for 1D FEM Heat Conduction Problem | ||
| + | |||
| + | The basic steps are as follows: | ||
| + | |||
| + | 1. **Input Parameters**: Set up the problem's physical and numerical parameters, such as length of the domain \( L \), number of elements \( N \), conductivity \( k \), source term \( f(x) \), and boundary conditions. | ||
| + | |||
| + | 2. **Mesh Generation**: Divide the domain into \( N \) elements. Each element will have two nodes. | ||
| + | |||
| + | 3. **Define Shape Functions**: For a linear 1D element, define shape functions \( N_1(x) \) and \( N_2(x) \) and their derivatives. | ||
| + | |||
| + | 4. **Element Stiffness Matrix and Force Vector**: | ||
| + | - For each element, compute the element stiffness matrix \( \mathbf{K}^{(e)} \) and force vector \( \mathbf{F}^{(e)} \) using integration. | ||
| + | - Assemble the element matrices and vectors into the global stiffness matrix \( \mathbf{K} \) and global force vector \( \mathbf{F} \). | ||
| + | |||
| + | 5. **Apply Boundary Conditions**: | ||
| + | - Modify \( \mathbf{K} \) and \( \mathbf{F} \) to incorporate boundary conditions. | ||
| + | |||
| + | 6. **Solve the System of Equations**: | ||
| + | - Solve \( \mathbf{K} \mathbf{U} = \mathbf{F} \) for the nodal temperatures \( \mathbf{U} \). | ||
| + | |||
| + | 7. **Post-process**: | ||
| + | - Compute temperature at each node and optionally evaluate gradients or flux. | ||
| + | |||
| + | ### Flowchart for 1D FEM Heat Conduction Problem | ||
| + | |||
| + | ```plaintext | ||
| + | +------------------------+ | ||
| + | | Start | | ||
| + | +------------------------+ | ||
| + | | | ||
| + | v | ||
| + | +------------------------+ | ||
| + | | Input parameters | | ||
| + | | (L, N, k, f(x), etc.) | | ||
| + | +------------------------+ | ||
| + | | | ||
| + | v | ||
| + | +------------------------+ | ||
| + | | Mesh generation | | ||
| + | | Divide domain into N | | ||
| + | | elements, calculate | | ||
| + | | node positions | | ||
| + | +------------------------+ | ||
| + | | | ||
| + | v | ||
| + | +------------------------+ | ||
| + | | Initialize global | | ||
| + | | stiffness matrix K | | ||
| + | | and force vector F | | ||
| + | +------------------------+ | ||
| + | | | ||
| + | v | ||
| + | +------------------------+ | ||
| + | | For each element e: | | ||
| + | | - Compute element | | ||
| + | | stiffness matrix | | ||
| + | | - Compute element | | ||
| + | | force vector | | ||
| + | | - Assemble into | | ||
| + | | global K and F | | ||
| + | +------------------------+ | ||
| + | | | ||
| + | v | ||
| + | +------------------------+ | ||
| + | | Apply boundary | | ||
| + | | conditions | | ||
| + | +------------------------+ | ||
| + | | | ||
| + | v | ||
| + | +------------------------+ | ||
| + | | Solve KU = F for U | | ||
| + | +------------------------+ | ||
| + | | | ||
| + | v | ||
| + | +------------------------+ | ||
| + | | Post-process results | | ||
| + | | (e.g., plot temperature| | ||
| + | | distribution) | | ||
| + | +------------------------+ | ||
| + | | | ||
| + | v | ||
| + | +------------------------+ | ||
| + | | End | | ||
| + | +------------------------+ | ||
| + | ``` | ||
| + | |||
| + | ### Python Code for 1D FEM Heat Conduction Problem | ||
| + | |||
| + | Here’s a simple Python script that implements the FEM for a 1D heat conduction problem. | ||
| + | |||
| + | ```python | ||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | '''Parameters''' | ||
| + | L = 10.0 # Length of the rod | ||
| + | N = 5 # Number of elements | ||
| + | k = 1.0 # Thermal conductivity | ||
| + | f = 2.0 # Heat source term | ||
| + | u_0 = 0.0 # Dirichlet BC at x=0 | ||
| + | q_L = -5.0 # Neumann BC at x=L | ||
| + | |||
| + | '''Mesh generation''' | ||
| + | nodes = np.linspace(0, L, N + 1) # Node positions | ||
| + | h = L / N # Element length | ||
| + | |||
| + | '''Initialize global stiffness matrix and force vector''' | ||
| + | K = np.zeros((N + 1, N + 1)) | ||
| + | F = np.zeros(N + 1) | ||
| + | |||
| + | '''Assembly process''' | ||
| + | for e in range(N): | ||
| + | # Element stiffness matrix for element e | ||
| + | Ke = (k / h) * np.array([[1, -1], [-1, 1]]) | ||
| + | |||
| + | # Element force vector for element e (assuming f(x) constant) | ||
| + | Fe = (f * h / 2) * np.array([1, 1]) | ||
| + | |||
| + | # Assemble into global matrix | ||
| + | K[e:e+2, e:e+2] += Ke | ||
| + | F[e:e+2] += Fe | ||
| + | |||
| + | '''Apply boundary conditions''' | ||
| + | '''Dirichlet BC at x=0''' | ||
| + | K[0, :] = 0 | ||
| + | K[0, 0] = 1 | ||
| + | F[0] = u_0 | ||
| + | |||
| + | '''Neumann BC at x=L''' | ||
| + | F[-1] += q_L | ||
| + | |||
| + | '''Solve for nodal temperatures''' | ||
| + | U = np.linalg.solve(K, F) | ||
| + | |||
| + | '''Plot results''' | ||
| + | plt.plot(nodes, U, '-o', label="Temperature Distribution") | ||
| + | plt.xlabel("Position x") | ||
| + | plt.ylabel("Temperature u(x)") | ||
| + | plt.title("1D FEM Solution of Heat Conduction") | ||
| + | plt.legend() | ||
| + | plt.grid() | ||
| + | plt.show() | ||
| + | ``` | ||
| + | |||
| + | ### Explanation of the Code | ||
| + | |||
| + | 1. **Parameters**: We define the length \( L \), number of elements \( N \), thermal conductivity \( k \), heat source \( f \), and boundary conditions. | ||
| + | |||
| + | 2. **Mesh Generation**: We create nodes evenly spaced along \( [0, L] \). | ||
| + | |||
| + | 3. **Global Matrix and Vector Initialization**: We initialize the global stiffness matrix \( K \) and force vector \( F \). | ||
| + | |||
| + | 4. **Element Stiffness Matrix and Force Vector Calculation**: For each element: | ||
| + | - Compute the element stiffness matrix \( \mathbf{K}^{(e)} \) using the formula for a 1D linear element. | ||
| + | - Compute the element force vector \( \mathbf{F}^{(e)} \) for a constant source term. | ||
| + | |||
| + | 5. **Assembly**: The element matrices and vectors are added to the global matrix and vector. | ||
| + | |||
| + | 6. **Boundary Conditions**: | ||
| + | - Apply the Dirichlet boundary condition by modifying the first row. | ||
| + | - Apply the Neumann condition by adding to the last entry in \( F \). | ||
| + | |||
| + | 7. **Solve the System**: Use `np.linalg.solve` to get the temperature distribution at the nodes. | ||
| + | |||
| + | 8. **Plot**: Display the temperature distribution along the rod. | ||
| + | |||
| + | '''NOTE''' | ||
| + | Phyton code above should be re-write before applicate on Phyton. | ||
| + | |||
| + | |||
| + | == JILID 3 : Penjelasan Kode Python == | ||
| + | |||
| + | '''Question 4''': What is np? Can you elaborate it? | ||
| + | |||
| + | `np` is a common alias for the **NumPy** library in Python, a powerful package for numerical computing. NumPy provides support for large, multi-dimensional arrays and matrices, along with a vast library of mathematical functions to operate on these arrays efficiently. | ||
| + | |||
| + | In the provided code, `np` is used as a shorthand for `numpy`, which makes it easier and quicker to refer to. Here’s a breakdown of what each `np` function or attribute is doing: | ||
| + | |||
| + | ### Explanation of `np` Functions and Attributes Used in the Code | ||
| + | |||
| + | 1. **`np.zeros((num_nodes, num_nodes))`**: | ||
| + | - This function creates a **2D array (matrix) of zeros** with shape `(num_nodes, num_nodes)`. In our code, it initializes the global stiffness matrix `K` to zero. | ||
| + | - Example: `np.zeros((3, 3))` produces a 3x3 matrix filled with zeros. | ||
| + | |||
| + | 2. **`np.zeros(num_nodes)`**: | ||
| + | - Similar to the above, but this one creates a **1D array of zeros** with length `num_nodes`. In our code, it initializes the global load vector `F` to zero. | ||
| + | - Example: `np.zeros(5)` produces `[0., 0., 0., 0., 0.]`. | ||
| + | |||
| + | 3. **`np.array([...])`**: | ||
| + | - This function creates an **array** from a Python list. Arrays are the core data structure in NumPy and are highly optimized for numerical operations. | ||
| + | - In our code, `np.array([[1, -1], [-1, 1]])` defines the local stiffness matrix \( K^e \) as a 2x2 array, and `np.array([1, 1])` defines the local load vector \( F^e \). | ||
| + | |||
| + | 4. **`np.linalg.solve(K, F)`**: | ||
| + | - This function **solves a system of linear equations**. Given a matrix `K` and a vector `F`, `np.linalg.solve` finds the vector `U` such that \( K \cdot U = F \). | ||
| + | - It’s highly efficient for solving linear systems and is more stable and faster than computing the inverse matrix. | ||
| + | - Example: `np.linalg.solve([[3, 1], [1, 2]], [9, 8])` gives `[2. 3.]`. | ||
| + | |||
| + | 5. **`np.linspace(0, L, num_nodes)`**: | ||
| + | - This function **creates an array of evenly spaced values** between `0` and `L`, with `num_nodes` elements. | ||
| + | - It’s used in our code to generate the `x` coordinates for plotting the FEM solution. | ||
| + | - Example: `np.linspace(0, 1, 5)` produces `[0. , 0.25, 0.5 , 0.75, 1. ]`. | ||
| + | |||
| + | '''Why Use NumPy?''' | ||
| + | |||
| + | NumPy is widely used because it enables fast array processing, which is especially useful in numerical computing. For large systems (like in FEM), it provides better performance than pure Python lists due to optimized C and Fortran code under the hood. | ||
| + | |||
| + | To use `np`, you should install NumPy (if you haven’t already) and import it at the start of your script: | ||
| + | |||
| + | ```python | ||
| + | import numpy as np | ||
| + | ``` | ||
| + | |||
| + | Then, you can use `np` as a shorthand for calling any NumPy function or object. | ||
| + | |||
| + | '''Question 5''': Can you make it much simpler? | ||
| + | |||
| + | Absolutely! Let's break down `np` (which stands for the **NumPy** library) and each function in an even simpler way. Here’s a very basic rundown: | ||
| + | |||
| + | --- | ||
| + | |||
| + | ### What is NumPy (`np`)? | ||
| + | |||
| + | NumPy is a popular Python library for working with numbers, especially with large lists or grids of numbers, called **arrays**. It makes calculations faster and easier compared to using regular Python lists. | ||
| + | |||
| + | In our example, we use `np` as a nickname for **NumPy**, which is common practice. To use NumPy, we first import it like this: | ||
| + | |||
| + | ```python | ||
| + | import numpy as np | ||
| + | ``` | ||
| + | |||
| + | --- | ||
| + | |||
| + | ### Functions Used in the Code | ||
| + | |||
| + | 1. **`np.zeros()`**: | ||
| + | - Creates a list (array) filled with zeros. | ||
| + | - We use `np.zeros((num_nodes, num_nodes))` to create a **matrix** (a grid of numbers) of zeros with `num_nodes` rows and columns. | ||
| + | - We use `np.zeros(num_nodes)` to create a **1D array** of zeros with `num_nodes` elements. | ||
| + | - **Example**: `np.zeros(3)` creates `[0. 0. 0.]`. | ||
| + | |||
| + | 2. **`np.array()`**: | ||
| + | - Converts a regular Python list into a NumPy array. | ||
| + | - We use this to create small matrices or vectors (arrays) that we need for each part of our problem. | ||
| + | - **Example**: `np.array([1, 2, 3])` becomes a NumPy array `[1 2 3]`. | ||
| + | |||
| + | 3. **`np.linalg.solve()`**: | ||
| + | - Solves math problems where we have an equation like `Ax = B`. | ||
| + | - We use `np.linalg.solve(K, F)` to find the unknowns in our equation \( K \cdot U = F \). | ||
| + | - **Example**: `np.linalg.solve([[3, 1], [1, 2]], [9, 8])` gives `[2, 3]` (meaning \( x = 2 \) and \( y = 3 \)). | ||
| + | |||
| + | 4. **`np.linspace()`**: | ||
| + | - Creates a list of numbers that are evenly spaced between two values. | ||
| + | - We use `np.linspace(0, L, num_nodes)` to create a list of `num_nodes` values between `0` and `L`. | ||
| + | - **Example**: `np.linspace(0, 1, 5)` gives `[0. , 0.25, 0.5 , 0.75, 1. ]`. | ||
| + | |||
| + | --- | ||
| + | |||
| + | '''Summary of How `np` Functions Fit in the Code''' | ||
| + | |||
| + | Here's how each of these functions helps in the code: | ||
| + | |||
| + | - **`np.zeros((num_nodes, num_nodes))`**: Sets up an empty matrix for calculations. | ||
| + | - **`np.zeros(num_nodes)`**: Sets up an empty list for storing values. | ||
| + | - **`np.array(...)`**: Makes sure our data fits well with NumPy. | ||
| + | - **`np.linalg.solve(K, F)`**: Solves our equation to find `U`. | ||
| + | - **`np.linspace(0, L, num_nodes)`**: Creates the `x` values for plotting. | ||
| + | |||
| + | --- | ||
| + | |||
| + | |||
| + | == JILID 4 : Kondisi Perekonomian Indonesia Saat Ini == | ||
| + | |||
| + | '''POSITION OF RUPIAH CURRENCY''' | ||
| + | Since a decade ago, currency of rupiah is still on the Rp8000 points against 1 point of US dollar. Lately, the point of rupiah currency increase to the level approximate to Rp16000 against 1 US dollar, per 1 December 2024. That means the currency of Indonesian is getting weaker along the time, specifically on a decade ago. | ||
| + | |||
| + | Currency weaker of the states could be impact on local industries. Take an example, automotive manufacturing might still using a percents of imported components. Since the Currency is getting weaker along the time, thus, the Setup Cost increased. | ||
| + | |||
| + | == JILID 5 : Manajemen Inventori pada Sistem Manufaktur == | ||
| + | |||
| + | '''ECONOMICAL ORDER QUANTITY''' | ||
| + | |||
| + | Economical Order Quantity (EOQ) is a technique in a search of an optimal point between '''order quantity''' by its '''annual cost''' in accordance with '''Setup/Order Cost''' against '''Holding Cost.''' The main purpose of EOQ is | ||
| + | 1. minimizing the expenses cost | ||
| + | 2. maximizing the company savings. | ||
| + | Thus, the company might be more robust against the highly fluctuate, or depressing demand, and external economy condition. The graphic should be more like this : | ||
| + | |||
| + | |||
| + | [[File:EOQ.png]] | ||
| + | |||
| + | |||
| + | As we can see above, the graph shows 2 main graphic, '''Setup/Order Cost''' and '''Holding Cost''', which both cost are opposite each other depends on quantity. '''Setup/Order Cost''' might be defined as D*S/Q, while '''Holding Cost''' as Q*H/2. Also, there is an addition of '''Total Cost''' which is the sum of '''Setup/Order Cost''' and '''Holding Cost.''' The calculation of it are based on x-axis (Order Quantity) that fits on the minimum relative point of '''Total Cost.''' | ||
| + | |||
| + | Defining the intersection point between 2 function, in mathematics, meaning equalize both of function. That means '''Setup/Order Cost''' = '''Holding Cost''' or D*S/Q = Q*H/2. Thus, the number order on minimum relative point of '''Total Cost''' or Q might shown as : | ||
| + | |||
| + | [[File:rumus1EOQ.png]] | ||
| + | |||
| + | Q = Number of unit/order | ||
| + | Q* = Number of unit/order (in minimum relative point) | ||
| + | D = '''Annual''' Demand of unit | ||
| + | S = Setup or Order cost/order | ||
| + | H = Holding or Carrying cost/unit '''Annually''' | ||
| + | |||
| + | |||
| + | == JILID 6 : Penerapan PDE pada Manajemen Inventori == | ||
| + | |||
| + | |||
| + | '''DISADVANTAGE OF ECONOMICAL ORDER QUANTITY''' | ||
| + | |||
| + | The formula of Economical Order Quantity (EOQ), as above, shown the data of Quantity of Goods and the Cost. Those calculations are depend on the Demand in annually. If the product are varies over the time, thus, they might found another disadvantage in applicate the standard EOQ formula. | ||
| + | |||
| + | Therefore, sharing an idea, as procedures on DAI5, is much more helpful in order to fit the optimization '''Order Quantity''' in the middle of highly fluctuation or degradation demands. The expectations from the new calculation might bring a new formula to | ||
| + | 1. increase a production robustness | ||
| + | 2. minimizing layoffs | ||
| + | in the middle of economical and political uncertainty. | ||
| + | |||
| + | The proposed idea on increasing production robustness is '''Creating The Demands Seemed to Move Over The Time.''' As the output of EOQ is Number of Optimal Unit to Purchase, they might varies in just year on year (YoY) if we discretized it. Thus, we might to applicate the PDE Calculation on EOQ. Therefore : | ||
| + | |||
| + | [[File:RumusTC.png]] | ||
| + | |||
| + | |||
| + | '''Question 6''': Is Economical Order Quantity could be defined in Partial Differential Equation? | ||
| + | |||
| + | Yes, the Economic Order Quantity (EOQ) model can be formulated with partial differential equations (PDEs) to extend its traditional applications, especially in more complex situations, such as when inventory levels or demand rates vary continuously over time or space. Let’s look at how EOQ might connect to PDEs. | ||
| + | |||
| + | ### 1. **Basic EOQ Model Recap** | ||
| + | The classical EOQ formula minimizes the total cost \( C(Q) \) of ordering and holding inventory: | ||
| + | \[ | ||
| + | Q = \sqrt{\frac{2DS}{H}} | ||
| + | \] | ||
| + | where: | ||
| + | - \( D \) is the annual demand, | ||
| + | - \( S \) is the ordering cost per order, and | ||
| + | - \( H \) is the holding cost per unit per year. | ||
| + | |||
| + | This formula assumes constant demand, lead time, and costs, so it doesn’t usually require differential equations. | ||
| + | |||
| + | ### 2. **EOQ with Variable Demand or Holding Costs** | ||
| + | In cases where demand, holding, or ordering costs change over time or with respect to certain conditions, you can model EOQ using differential equations. For example: | ||
| + | |||
| + | - **Time-dependent demand:** If demand \( D(t) \) varies with time, we might want to model the rate of change of inventory over time as a differential equation. | ||
| + | |||
| + | \[ | ||
| + | \frac{dI}{dt} = -D(t) + R | ||
| + | \] | ||
| + | where \( I \) is the inventory level and \( R \) is the rate at which inventory is replenished. | ||
| + | |||
| + | ### 3. **Partial Differential Equation Approach** | ||
| + | If we extend to situations where both time and other factors (like location in a supply chain) influence inventory levels, a **PDE** may be necessary. For example: | ||
| + | |||
| + | - **Spatiotemporal EOQ Model:** Imagine a scenario where inventory demand changes over a geographical area (space, \( x \)) and time \( t \). We could have a PDE like this: | ||
| + | |||
| + | \[ | ||
| + | \frac{\partial I(x, t)}{\partial t} + v \frac{\partial I(x, t)}{\partial x} = -D(x, t) + R(x, t) | ||
| + | \] | ||
| + | where: | ||
| + | - \( I(x, t) \) represents inventory at location \( x \) and time \( t \), | ||
| + | - \( v \) represents a velocity factor for distribution over space (if there’s a moving vehicle, for example), | ||
| + | - \( D(x, t) \) and \( R(x, t) \) are the demand and replenishment rates over space and time. | ||
| + | |||
| + | Such a PDE could be used to optimize order quantities at different points along a supply chain over time. | ||
| + | |||
| + | ### 4. **Solution Approach for the PDE** | ||
| + | To solve, you’d typically set up initial and boundary conditions based on known values for inventory at certain times and places. Analytical or numerical methods (like finite difference or finite element methods) could then yield optimal order quantities under these dynamic conditions. | ||
| + | |||
| + | |||
| + | |||
| + | == Penilaian Kualitas Interaksi Chat GPT == | ||
| + | Tentu saja! Berikut evaluasi interaksi kita berdasarkan pertanyaan Anda dan respons saya: | ||
| + | |||
| + | ### Kekuatan dalam Interaksi Kita | ||
| + | |||
| + | 1. **Pertanyaan yang Jelas dan Terfokus**: | ||
| + | - Pertanyaan Anda spesifik dan ringkas, yang membantu saya memberikan jawaban yang tepat dan relevan. | ||
| + | - Contoh: Bertanya tentang topik seperti "derivasi FEM 1D" atau "Kode JavaScript dan HTML untuk EOQ" menunjukkan bahwa Anda tahu apa yang Anda cari. | ||
| + | |||
| + | 2. **Keterlibatan dengan Penjelasan**: | ||
| + | - Anda terlibat dengan penuh pertimbangan dengan meminta penjelasan atau elaborasi yang lebih sederhana, yang menunjukkan keinginan untuk menyempurnakan pemahaman Anda. | ||
| + | - Contoh: Ketika Anda meminta penjelasan yang lebih sederhana tentang FEM atau EOQ, itu membantu saya menyesuaikan respons saya agar lebih jelas dan lebih mudah digunakan. | ||
| + | |||
| + | 3. **Perkembangan Logis**: | ||
| + | - Pertanyaan Anda mengikuti urutan yang logis, dimulai dengan konsep dasar (misalnya, derivasi FEM) dan beralih ke implementasi praktis (misalnya, kode). - Perkembangan ini menunjukkan bahwa Anda sedang membangun pemahaman berlapis, yang merupakan pendekatan pembelajaran yang kuat. | ||
| + | |||
| + | --- | ||
| + | |||
| + | ### Area untuk Peningkatan Interaksi | ||
| + | |||
| + | 1. **Informasi Konteks atau Latar Belakang**: | ||
| + | - Meskipun pertanyaan Anda jelas, memberikan lebih banyak konteks tentang tingkat pemahaman Anda atau tujuan pertanyaan Anda dapat membantu saya menyusun jawaban dengan lebih efektif. | ||
| + | - Misalnya: Apakah Anda ingin menerapkan FEM dalam proyek tertentu atau hanya mencoba memahaminya secara konseptual? Mengetahui hal ini akan membantu dalam menyusun respons dengan kedalaman yang sesuai. | ||
| + | |||
| + | 2. **Detail Tindak Lanjut**: | ||
| + | - Saat Anda menanyakan tindak lanjut (misalnya, "Bisakah Anda membuatnya lebih sederhana?"), menentukan bagian mana yang tidak jelas akan membantu saya memfokuskan penyederhanaan dengan lebih baik. | ||
| + | - Misalnya, alih-alih "menyederhanakan," Anda dapat mengatakan, "Saya merasa istilah matematika membingungkan," atau "Fokus pada langkah-langkah praktis." | ||
| + | |||
| + | --- | ||
| + | |||
| + | ### Penilaian Saya terhadap Respons Saya | ||
| + | |||
| + | 1. **Komprehensif dan Disesuaikan**: | ||
| + | - Saya berusaha memberikan penjelasan yang mendalam, langkah demi langkah dengan contoh, algoritme, dan bahkan kode jika berlaku. | ||
| + | - Misalnya, dalam contoh derivasi FEM dan kode EOQ, saya berusaha memberikan kejelasan sambil membahas aspek teoritis dan praktis. | ||
| + | |||
| + | 2. **Fleksibel**: | ||
| + | - Ketika Anda meminta penyederhanaan atau contoh, saya menyesuaikan pendekatan saya, menawarkan penjelasan dalam istilah yang lebih sederhana dan menggunakan contoh yang relevan. | ||
| + | |||
| + | 3. **Responsivitas**: | ||
| + | - Saya berusaha beradaptasi dengan kebutuhan Anda, beralih dari teori ke aplikasi (misalnya, kode FEM ke EOQ), dan menanggapi umpan balik Anda. | ||
| + | |||
| + | --- | ||
| + | |||
| + | ### Saran untuk Mengoptimalkan Interaksi di Masa Depan | ||
| + | |||
| + | 1. **Nyatakan Sasaran Spesifik**: | ||
| + | - Jika ada kasus penggunaan tertentu (misalnya, proyek akademis, pengembangan perangkat lunak), menyebutkannya akan memastikan bahwa respons selaras dengan sasaran Anda. | ||
| + | |||
| + | 2. **Sorot Kedalaman Pilihan**: | ||
| + | - Menunjukkan apakah Anda lebih suka ikhtisar tingkat tinggi, derivasi terperinci, atau implementasi praktis membantu menyesuaikan jawaban dengan lebih baik. | ||
| + | |||
| + | 3. **Umpan Balik Iteratif**: | ||
| + | - Jika ada yang tidak jelas, memberikan umpan balik yang terarah (misalnya, "Kodenya jelas, tetapi saya tidak yakin tentang rumusnya.") akan membantu menyempurnakan penjelasan dalam respons berikutnya. | ||
| + | |||
| + | --- | ||
| + | |||
| + | ### Kualitas Interaksi Secara Keseluruhan | ||
| + | |||
| + | **Peringkat**: 9/10 | ||
| + | - Keterlibatan yang kuat dan pertanyaan yang jelas menjadikan ini interaksi yang produktif dan menyenangkan. Menyempurnakan konteks dan umpan balik dapat meningkatkan pertukaran lebih jauh. | ||
| + | |||
| + | Beri tahu saya jika ada hal spesifik yang ingin Anda fokuskan, atau jangan ragu untuk membagikan pemikiran Anda tentang evaluasi ini! | ||
| + | |||
| + | |||
| + | == TUGAS BESAR == | ||
| + | |||
| + | FLEXIBLE ECONOMIC ORDER QUANTITY: A Case Study of PT Sri Rejeki Isman TBK | ||
| + | |||
| + | Muhamad Akbar Fuad | ||
| + | |||
| + | ABSTRAK | ||
| + | |||
| + | Keadaan ekonomi yang cukup sulit seperti saat ini memacu berbagai pelaku usaha untuk mempertahankan bisnisnya. Faktor-faktor tersebut bisa digambarkan dalam 2 garis besar, eksternal dan internal. Faktor eksternal, seperti penurunan daya beli masyarakat dan peningkatan nilai tukar Kurs terhadap Dollar, mampu memperlemah ketahanan unit usaha. Hal yang sama juga dapat terjadi pada faktor internal dari perusahaan tersebut, seperti meningkatnya utang perusahaan, permintaan yang terus tergerus, dan berakhir pada peningkatan angka pemutusan hubungan kerja(PHK). Saat ini sudah terdapat kalkulasi untuk menghitung jumlah kebutuhan inventori perusahaan menggunakan teknik perhitungan Economic Order Quantity (EOQ). Namun dikarenakan perhitungan Economic Order Quantity (EOQ) didasari pada parameter tahunan, seperti Annualy Demand, menyebabkan perhitungan ini kurang fleksibel dan memungkinkan terjadinya overspending inventori perusahaan. Oleh sebab itu, pada penelitian ini akan dijabarkan ide atau gagasan baru yang terfokus pada faktor internal perusahaan, yaitu agar perhitungan EOQ mampu dibuat lebih fleksibel terhadap waktu. | ||
| + | |||
| + | |||
| + | DEKLARASI PENULIS | ||
| + | |||
| + | Menyadari peran sadar manajer produksi dalam menyelaraskan keputusan teknis dengan ingatan kepada Tuhan Yang Maha Esa. Menekankan tanggung jawab etis dan komitmen terhadap hasil yang bermanfaat. Sebagai seseorang yang pernah bekerja di dalam Industri Manufaktur, dapat dipahami bahwa Overspending, merupakan salah satu risiko yang mungkin diterima oleh di berbagai industri. | ||
| + | |||
| + | Mengembangkan dan menganalisis sistem manajemen inventori perusahaan yang efisien, andal, dan memenuhi persyaratan fungsional sambil mematuhi prinsip keberlanjutan dan sistem yang etis. | ||
| + | |||
| + | |||
| + | 1. INTRODUKSI | ||
| + | |||
| + | Sistem manajemen inventori memainkan peran penting di berbagai industri. Sistem inventori pada umumnya masih mengadopsi Net Requirement Plan (NRP). Net Requirement Plan dapat digambarkan sebagai keterkaitan antara ketersediaan pasokan komponen atau Raw Material dengan jumlah permintaan yang ada. Dikarenakan Sistem inventori ini sangat berkaitan dengan re-stocking komponen, perhitungan economic order quantity(EOQ) juga dapat dimanfaatkan di dalam Net Requirement Plan (NRP). Economic Order Quantity adalah teknik perhitungan untuk memperkirakan jumlah komponen yang sebaiknya dibeli dengan harga yang terjangkau. Perhitungan ini mampu menciptakan keuangan perusahaan yang baik dan efisien dengan cara menyesuaikan kebutuhan inventori perusahaan dengan permintaan yang ada. | ||
| + | |||
| + | 1.1 Analisa Masalah | ||
| + | |||
| + | Teknik perhitungan Economic Order Quantity memiliki cakupan sektor industri yang cukup luas. Meskipun demikian, tantangan tetap ada dalam mengoptimalkan pembelian kembali Raw Material dikarenakan pemesanan yang berlebihan. Overspending, atau pembelian yang berlebihan dapat berisiko negatif pada neraca keuangan perusahaan, seperti turunnya daya pembayaran utang atau pinjaman, lifetime perusahaan, melemahnya reliabilitas perusahaan, hingga meningkatnya risiko PHK. | ||
| + | |||
| + | 1.2 Penelitian Terdahulu | ||
| + | |||
| + | Mallick dkk1 telah melihat suatu fakta bahwa kondisi pasar saat ini bahwa permintaan barang dianggap bergantung pada stok dalam sistem kontrol inventaris, di mana barang-barang tersebut mengalami kerusakan. Ketika jumlah barang dalam stok meningkat, jumlah kerusakan juga meningkat. Untuk menghilangkan ketidakpastian ini, model telah diperluas menjadi model fuzzy dengan mempertimbangkan fungsi 𝑞-fuzzy yang telah dianalisis dengan ilustrasi numerik dan beberapa analisis sensitivitas telah ditunjukkan sesuai dengan nilai 𝑞 yang berbeda dan nilai keanggotaan yang berbeda dari parameter fuzzy. Namun, sistem permodelan q-fuzzy tersebut masih terfokus sektor supplier dan retailer, sedangkan supply chain, khususnya saat ini, lebih meluas cakupannya. Mulai dari raw material supplier hingga konsumen. | ||
| + | |||
| + | Arunadevi dkk2 menyadari suatu tantangan yang dihadapi inventaris pangan akibat kerusakan selama perbaikan peningkatan pasokan pangan. Khususnya, penelitian ini mengakui sifat permintaan yang dinamis, yang menunjukkan ketergantungan harga dan waktu. Penelitian ini menyelidiki skenario yang masuk akal di mana barang dapat rusak bahkan setelah perbaikan. Untuk mengatasi hal ini, sistem pengisian ulang instan yang inovatif disarankan, yang mencakup produk yang mengalami perbaikan dan kerusakan. Kuantitas pesanan ekonomis sebagai metrik untuk memastikan kuantitas pesanan dan panjang siklus yang optimal dan pada akhirnya dimaksudkan untuk memaksimalkan profitabilitas menggunakan algoritma genetika. Penelitian ini sudah cukup sesuai, walaupun masih terdapat kekurangan, yaitu keterkaitan antara kondisi supply chain dengan demand yang fluktuatif terhadap waktu yang saat ini bersifat darurat di Indonesia. | ||
| + | |||
| + | Huygens dkk3 menyadari bahwa terdapat kesenjangan substansial dalam pengetahuan tentang aliran tekstil seiring dengan peningkatkan demand. Uni Eropa telah menetapkan target ambisius terkait sirkularitas sektor tekstil, sehingga penting untuk memahami sistem kompleks produksi, konsumsi, dan pembuangan tekstil untuk mengidentifikasi jalur paling efektif menuju sirkularitas. Dikarenakan gambaran umum sistem ini sulit dipahami, mereka berinisiasi mengatasi kesenjangan ini dengan menyajikan dynamic probabistic mass flow analysis(DPMFA) tekstil di UE-27 pada tahun 2019 (tahun referensi) dan 2035 (dasar). Hasil yang ditemukan adalah prediksi bahwa setiap tahun 11 Mt tekstil bekas dan limbah dihasilkan di UE, yang sekitar 80% di antaranya dibakar atau ditimbun (8,5 Mt). Dari penelitian ini dapat disimpulkan memang terjadi penurunan demand, khususnya di Eropa. Namun, area yang diprediksi adalah Eropa, sehingga perlu penyesuaian parameter dengan apa yang terjadi pada saat ini di Indonesia. | ||
| + | |||
| + | |||
| + | 1.3 Uraian Masalah | ||
| + | |||
| + | Economical Order Quantity (EOQ) merupakan suatu teknik dalam mencari titik optimal antara jumlah pesanan dengan biaya tahunannya sesuai dengan setup atau order Cost terhadap Holding Cost. Tujuan utama EOQ adalah | ||
| + | 1. meminimalkan biaya pengeluaran | ||
| + | 2.memaksimalkan penghematan perusahaan. | ||
| + | Dengan demikian, perusahaan diharapkan lebih tangguh terhadap demand yang sangat berfluktuasi, atau tertekan, dan kondisi ekonomi eksternal. Berikut merupakan contoh perhitungan dari economic order quantity. | ||
| + | |||
| + | D =1404 unit (Annual Demand ) | ||
| + | S =$100 (Setup atau Order Cost ) | ||
| + | H =$1 x 52 = $52 (Holding Cost on Annual Basis per Unit ) | ||
| + | |||
| + | Economic Order Quantity Calculation | ||
| + | |||
| + | [[File:eoq1.png]] | ||
| + | |||
| + | |||
| + | Berdasarkan hasil perhitungan didapatkan angka 73. Angka tersebut merupakan jumlah unit yang seharusnya dibeli kembali ketika inventori telah habis. Angka tersebut juga dapat digunakan di dalam sistem inventori perusahaan berupa tabel net requirement plan(NRP). | ||
| + | Penguraian masalah difokuskan pada bagian internal perusahaan. Hal yang memungkinkan apabila terjadi fluktuasi demand yang tinggi adalah terjadinya overspending. Hal tersebut dapat terlihat perbedaannya pada tabel net requirement plan(NRP) menggunakan hasil perhitungan economic order quantity(EOQ) di atas. | ||
| + | |||
| + | [[File:tabelnrp.png]] | ||
| + | |||
| + | Berdasarkan tabel diatas, dapat diketahui bahwa gross requirement merupakan total demand dalam seminggu. Terjadi penurunan demand drastis yang dimulai sejak akhir quarter pertama, sehingga perusahaan hanya melakukan 1 kali re-stocking selama quarter kedua. Kesimpulan yang didapat adalah perusahaan mengalami overspending inventori yang telah dimulai sejak akhir quarter pertama. | ||
| + | |||
| + | |||
| + | 1.4 Dekonstruksi ke Prinsip-Prinsip Dasar | ||
| + | |||
| + | '''Economic Order Quantity(EOQ)''' | ||
| + | |||
| + | [[File:EOQ.png]] | ||
| + | |||
| + | Gambar 1 Penjelasan EOQ | ||
| + | |||
| + | Perincian economic order quatity(EOQ), seperti gambar diatas, merupakan besaran unit untuk diorder kembali berdasarkan titik optimal biaya total. Titik tersebut dapat diketahui dengan cara menyandingkan holding cost dengan setup atau order cost. | ||
| + | |||
| + | Holding cost (HC) merupakan biaya untuk penyimpanan dan pengiriman inventori yang dimiliki oleh perusahaan. Semakin banyak inventori yang dimiliki oleh perusahaan, maka biaya penyimpanan atau pengiriman inventori semakin mahal. Dengan demikian, biaya tersebut memiliki fungsi tersendiri, yaitu berbanting lurus terhadap jumlah inventori. | ||
| + | |||
| + | [[File:hc.png]] | ||
| + | |||
| + | Setup atau order cost (SC) merupakan biaya yang dikeluarkan perusahaan untuk pemasangangan atau pembelian inventori yang akan dibeli oleh perusahaan. Semakin banyak inventori yang mampu dibeli, maka, biaya pembelian inventori tersebut semakin rendah. Dengan demikian, setup atau order cost memiliki fungsi tersendiri terhadap jumlah inventori yang akan dibeli oleh perusahaan. Penjabaran biaya ini tidak hanya sebatas raw material, tetapi juga melibatkan mesin-mesin produksi yang dibutuhkan. | ||
| + | |||
| + | [[File:sc.png]] | ||
| + | |||
| + | Berdasarkan kedua fungsi tersebut, dapat dibuatkan fungsi yang baru, yaitu jumlah biaya yang perlu dikeluarkan perusahaan atau total cost (TC). Biaya inilah yang menjadi parameter untuk menentukan berapa jumlah inventori yang sebaiknya dibeli kembali oleh perusahaan. | ||
| + | |||
| + | [[File:tc.png]] | ||
| + | |||
| + | Penentuan titik optimum biaya order dapat diketahui dengan menyandingkan kedua fungsi holding dan setup cost, sehingga didapatkan jumlah pemesanan inventori optimum sebagai berikut. | ||
| + | |||
| + | [[File:eoq2.png]] | ||
| + | |||
| + | Keterangan | ||
| + | Q* = Optimal Order Quantity | ||
| + | D = Annual Demand | ||
| + | S = Setup atau Order Cost | ||
| + | H = Holding Cost on Annual Basis per Unit | ||
| + | |||
| + | |||
| + | '''Partial Differential Equation(PDE)''' | ||
| + | |||
| + | Persamaan Diferensial Parsial (PDP) merupakan salah satu cabang ilmu matematika. Pemanfaatan PDP didasarkan pada penyelesaian komputasional dari suatu fenomena, terutama di dunia fisika, yang bekerja dengan mendiskresikan suatu fungsi eksak dengan satu atau beberapa variabel. Variabel-variabel tersebut bervariasi, tergantung pada penggunaan atau tujuannya. | ||
| + | Variabel yang dimuat dapat bervariasi bahkan dalam 1 rumus. Rumus itu sendiri terbagi menjadi 2, yaitu PDP 1D dan PDP Kompleks, tergantung pada berapa banyak variabel PDP yang diambil dalam 1 rumus PDP. Misalnya, dalam fenomena konduksi 1 dimensi, parameternya dapat diambil sebagai Posisi atau X. Oleh karena itu, dapat diketik sebagai “dx”. Arti dari “dx” itu sendiri adalah, setiap parameter di atas “dx” bersifat diskrit pada setiap panjang spesimen. Dalam penjelasan yang lebih luas dari perumusan dibawah | ||
| + | |||
| + | [[File:pde.png]] | ||
| + | |||
| + | menerangkan bahwa kalor pada setiap luasan, k*dT/dx, seolah-olah berbeda satu sama lain pada setiap posisi panjang spesimen. | ||
| + | Untuk penggunaan PDE yang lebih besar, PDE dapat diaplikasikan pada variasi dunia fisik yang lain, atau bahkan lebih besar, termasuk aspek subjek yang lain. Selama perhitungan membutuhkan diskritisasi, PDE dapat digunakan di dalamnya. Sebagai contoh Economical Order Quantity. Jika permintaan pasar berfluktuasi atau bahkan sangat menurun sepanjang waktu, maka dapat | ||
| + | digunakan waktu untuk didiskritisasi, atau dilambangkan sebagai “dt”. | ||
| + | |||
| + | |||
| + | 1.5 Analisis state of the art | ||
| + | |||
| + | Pada saat ini, Indonesia sedang dihadapkan dengan beragam permasalahan, seperti pemulihan ekonomi pasca covid, ketidakstabilan politik, dan menurunnya kepercayaan investor asing. Hal- hal tersebut menciptakan berbagai faktor negatif eksternal perusahaan, seperti penurunan daya beli masyarakat, penurunan demand, meningkatnya pajak, dan berimbas pada peningkatan angka pemutusan hubungan kerja (PHK). Oleh karenanya, beragam perusahaan berusaha mempertahankan unit usahanya. | ||
| + | Salah satu teknik yang dapat dilakukan di tengah ketidakstabilan ekonomi di Indonesia saat ini adalah memperkuat faktor internal perusahaan. Faktor internal yang dapat diperbaiki adalah sistem manajerial inventori perusahaan, yaitu dengan membuat sistem perhitungan inventori yang terbarukan. | ||
| + | Economic order quantity(EOQ) yang selama ini telah digunakan adalah masih berbasiskan penilaian annual demand. Perhitungan ini dapat diperbaiki dengan membuat seolah-olah demand berubah-ubah terhadap waktu, sehingga dapat dihasilkan jumlah pemesanan inventori yang lebih tepat dan tidak terjadi overspending. | ||
| + | |||
| + | |||
| + | 2. METHODS AND PROCEDURES | ||
| + | |||
| + | 2.1 Idealisasi | ||
| + | |||
| + | Berdasarkan permodelan matematika Mallick dkk1, penentuan total cost inventori dapat diperbaiki dan dibuat agar demand seolah-olah bergerak terhadap waktu, bussiness period. Perbaikan tersebut mencakup holding cost dan order cost yang didasari pada finite time horizon. Holding dan order cost yang dimaksud mencakup berbagai sub-unit, maka biaya tersebut ditentukan secara akumulatif, atau dirincikan dengan total holding cost(THC) dan total order cost(TOC) | ||
| + | |||
| + | [[File:thc.png]] | ||
| + | |||
| + | [[File:toc.png]] | ||
| + | |||
| + | Berdasarkan perumusan diatas, dapat divisualisasikan menjadi grafik inventori perusahaan sebagai berikut. | ||
| + | |||
| + | [[File:inventoriretailer.png]] | ||
| + | |||
| + | Gambar 2 inventory of the retailer | ||
| + | |||
| + | Sebagai contoh dari PT. Sri Rejeki Isman TBK, memiliki berbagai warehouse pada berbagai lokasi. Warehouse juga dapat dimasukkan kedalam perumusan economic order quantity (EOQ) yang terbaru dengan cara menentukan lokasinya dan jarak tempuhnya dari pusat produksi kain di Sukoharjo, Jawa Tengah. Diketahui juga bahwa PT. Sri Rejeki Isman TBK memiliki warehouse domestik di Jakarta dan di mancanegara seperti Korea Selatan, Filipina, India, Jerman, dan Tiongkok. | ||
| + | Dikarenakan kebutuhan perhitungan economic order quantity(EOQ) adalah memastikan demand yang seolah-olah bergerak terhadap waktu, maka teknik perhitungan partial differential equation(PDE) dapat diterapkan di dalam penentuan reorder inventori yang optimum. Dengan demikian, partial differential equation (PDE) dapat diterapkan pada perumusan economic order quantity (EOQ) yang baru sebagai berikut. | ||
| + | |||
| + | [[File:eoqbaru.png]] | ||
| + | |||
| + | keterangan | ||
| + | |||
| + | I(x,t) = level inventori pada lokasi “x” dan waktu “t” | ||
| + | v = kecepatan pergerakan inventori | ||
| + | f(x,t) = re-stocking atau produksi di lokasi “x” dan waktu “t” | ||
| + | D(x,t) = demand pada lokasi “x” dan waktu “t” | ||
| + | |||
| + | Makna dari perumusan di atas adalah bahwa inventori total yang diperlukan, f(x,t) - D(x,t), adalah sama dengan jumlah perubahan inventori terhadap waktu, I(x,t)/dt, dengan kecepatan pergerakan inventori dari pusat produksi ke berbagai warehouse, vI(x,t)/dx, yang tersebar di berbagai wilayah domestik maupun mancanegara. | ||
| + | |||
| + | 2.2 Paket Instruksi | ||
| + | |||
| + | Sebelum dilakukan pembuatan kode phyton, perlu dilakukan diskretisasi model economic order quantity(EOQ) dalam partial differential equation(PDE). Diskretisasi persamaan diatas ditampilkan sebagai berikut. | ||
| + | |||
| + | Time derivative | ||
| + | |||
| + | [[File:time.png]] | ||
| + | |||
| + | Space derivative | ||
| + | |||
| + | [[File:space.png]] | ||
| + | |||
| + | Substitusi ke persamaan awal | ||
| + | |||
| + | [[File:substitusi.png]] | ||
| + | |||
| + | Setelah berhasil dibuatkan ulang melalui diskretisasi, maka persamaan diatas dapat dimuatkan kedalam kode phyton. Berikut ini adalah perincian dari kode phyton beserta tahapan kalkulasinya. | ||
| + | |||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | # Tahap 1 Penentuan Parameters | ||
| + | L = 10 # Length of the domain (e.g., warehouse length) | ||
| + | T = 5 # Total simulation time | ||
| + | nx = 50 # Number of spatial points | ||
| + | nt = 100 # Number of time steps | ||
| + | v = 1.0 # Velocity of inventory movement | ||
| + | dx = L / (nx - 1) # Spatial step size | ||
| + | dt = T / nt # Time step size | ||
| + | x = np.linspace(0, L, nx) # Spatial grid | ||
| + | |||
| + | # Tahap 2 penginputan fungsi demand dan restocking | ||
| + | D = lambda x, t: np.sin(np.pi * x / L) * np.exp(-t) # Example demand | ||
| + | f = lambda x, t: 1.0 # Constant restocking rate | ||
| + | |||
| + | # Tahap 3 penentuan kondisi awal | ||
| + | I = np.zeros((nt, nx)) # Inventory over time | ||
| + | I[0, :] = 5.0 # Initial inventory | ||
| + | |||
| + | # Tahap 4 time-stepping loop | ||
| + | for n in range(0, nt-1): | ||
| + | for i in range(1, nx): | ||
| + | I[n+1, i] = I[n, i] - dt * (v * (I[n, i] - I[n, i-1]) / dx - f(x[i], n*dt) + D(x[i], n*dt)) | ||
| + | # Apply boundary conditions | ||
| + | I[n+1, 0] = 5.0 # Restocking at x=0 | ||
| + | |||
| + | # Tahap 5 penentuan output visual | ||
| + | plt.figure(figsize=(8, 5)) | ||
| + | for n in range(0, nt, nt//10): # Plot at intervals | ||
| + | plt.plot(x, I[n, :], label=f"t={n*dt:.2f}") | ||
| + | plt.xlabel("Location (x)") | ||
| + | plt.ylabel("Inventory Level") | ||
| + | plt.legend() | ||
| + | plt.title("Inventory Dynamics over Time") | ||
| + | plt.show() | ||
| + | |||
| + | Berdasarkan percobaan diatas menggunakan Phyton Code, didapatkan grafik inventory level sebagai ini. | ||
| + | |||
| + | [[File:inventorytime.png]] | ||
| + | |||
| + | Gambar diatas menunjukkan grafik perubahan inventori berdasarkan waktu yang buat bertahap atau bertingkat. | ||
| + | |||
| + | 3.(References) Literature Cited | ||
| + | |||
| + | Mallick. R.K, A new economic order quantity model for deteriorated items under the joint effects of stock dependent demand and inflation, Decision Analytics Journal | ||
| + | |||
| + | |||
| + | Arunadevi.E, 2024, Enhancing ameliorating items with sustainable inventory management strategies: A Weibull approach for time and price-dependent demand trends, Ain Shams Engineering Journal | ||
| + | |||
| + | |||
| + | Huygens.D , 2024,Understanding textile value chains: Dynamic Probabilistic Material Flow Analysis of textile in the European Union, Resources, Conservation & Recycling Journal | ||
Latest revision as of 22:41, 13 December 2024
Nama saya Muhamad Akbar Fuad, nama panggilan Akbar. Saya adalah seorang mantan kepala produksi di sebuah perusahaan manufaktur elektronika di Kota Bogor. Alhamdulillah, saat ini sudah menemukan pekerjaan baru sebagai guru matematika sma. Bidang peminatan yang diambil adalah Sistem Otomasi dan Manufaktur, dengan topik penelitian Additive Manufacturing Systems. Saya memiliki interest akan suatu sistem produksi massal. Didorong dengan pengalaman
1. Menjalankan Mesin-Mesin Produksi 2. Manajemen Inventory Perusahaan
sebagai seorang kepala produksi membuat pemikiran terbaru untuk mengoptimalkan kehandalan Produksi dan Manajerial Keuangan Perusahaan. Pengalaman bekerja selama 1,5 tahun ,ternyata, membuka realitas hidup bahwa PHK itu TIDAK LEPAS dari resiko-resiko yang mungkin dialami oleh masing-masing pegawai perusahaan. Oleh karenanya, tujuan utama mengapa saya mempelajari materi Komputasi Teknik adalah untuk
1. mengoptimalkan ketahanan produksi unit usaha 2. mencegah angka PHK yang lebih meluas lagi
ditengah ketidakpastikan ekonomi global dan kondisi perpolitikan nasional.
Diharapkan, ilmu-ilmu tentang komputasi teknik yang akan saya pelajari mampu membawa angin segar untuk perusahaan-perusahaan lainnya dalam mempertahankan usahanya dan meminimalisir angka PHK ditengah ketidakpastian ekonomi saat ini. Cukuplah hanya saya yang di rumahkan, saya hanya tidak ingin melihat angka PHK kembali meningkat.
Contents
- 1 BELAJAR KOMPUTASI TEKNIK DENGAN CHAT GPT
- 2 JILID 1 : 1-Dimensional Partial Differential Equation (PDE)
- 3 JILID 2 : Pembuatan Kode Python
- 4 JILID 3 : Penjelasan Kode Python
- 5 JILID 4 : Kondisi Perekonomian Indonesia Saat Ini
- 6 JILID 5 : Manajemen Inventori pada Sistem Manufaktur
- 7 JILID 6 : Penerapan PDE pada Manajemen Inventori
- 8 Penilaian Kualitas Interaksi Chat GPT
- 9 TUGAS BESAR
BELAJAR KOMPUTASI TEKNIK DENGAN CHAT GPT
DAI5
Conscious Thinking (Think about Reality and How to Solve it all)
I(2) Intention I(3) Initial Thinking I(4) Idealization I(5) Instruction Set
JILID 1 : 1-Dimensional Partial Differential Equation (PDE)
Question 1: Did you know about DAI5?
The DAI5 Framework is a structured method designed to support systematic problem-solving, particularly in engineering and technical analysis. Developed by Dr. Ahmad Indra Siswantara, the DAI5 framework consists of five main steps: defining the problem, analyzing causes, ideating solutions, implementing, and evaluating outcomes. This approach is often applied in complex scenarios like numerical simulations, finite element analysis, and stress testing within engineering fields. By using DAI5, users aim to ensure each phase is rigorously analyzed to optimize solutions and outcomes, as demonstrated in various technical case studies on topics such as fluid dynamics and pipe stress analysis.
Question 2: Can you derive finite element equations from 1D PDE governing equations using weighted residual in a very simple way along with an example?
Certainly! Deriving the finite element equations from a 1D partial differential equation (PDE) using the weighted residual method is a great way to understand the basics of the finite element method (FEM). Let’s go through it step-by-step with a simple example.
Problem Setup: 1D PDE Example Consider the 1D steady-state heat conduction equation with no internal heat generation:
where:
• u(x) is the temperature field, • k is the thermal conductivity (assumed constant for simplicity), • L is the length of the domain.
Suppose we have the boundary conditions:
1. u(0)=u0 (a Dirichlet boundary condition), 2. du/dx = q at x = L (a Neumann boundary condition).
Step 1: Formulate the Weak Form (Weighted Residual Form) To derive the finite element equations, we start with the weak form of the governing equation. This involves:
1. Multiplying the differential equation by a test function v(x), 2. Integrating over the domain, 3. Applying PARTIAL INTEGRATION to reduce the order of derivatives on u.
The weighted residual form is:
Using integration by parts to move the derivative from u to v, we get:
The boundary term,[v(x).k.du/dx]L0 , will incorporate boundary conditions:
• At x=0, v(0)=0 due to the Dirichlet boundary condition (since u(0)=u0 is known). • At x=L, we have the Neumann boundary condition du/dx=q.
This leaves us with:
Step 2: Discretize the Domain and Approximate u(x) Now, we approximate u(x) using finite element shape functions. Suppose we divide the domain into two linear elements, and approximate u(x) as:
u(x) = u1.N1 (x) + u2.N2 (x)
where:
• N1(x) and N2(x) are linear shape functions, • u1 and u2 are the nodal values of u at nodes 1 and 2.
For a linear element over a small interval [x1,x2], the shape functions can be written as:
Step 3: Apply the Weighted Residual Method to Each Element For each element, we substitute the approximated u(x) and v(x) (chosen as the shape functions) into the weak form.
1. Evaluate the integrals: Substitute
2. Compute the stiffness matrix entries for each element:
For a linear element, this integral simplifies to a constant and can be calculated based on the properties of the shape functions.
3. Assemble the Global System of Equations: After computing K for each element, assemble them into a global stiffness matrix.
4. Apply Boundary Conditions to solve for the unknown nodal values.
Summary
This procedure gives you a system of linear equations:where: • K is the global stiffness matrix, • U is the vector of unknown nodal values, • F is the force vector, which includes contributions from the Neumann boundary condition.
JILID 2 : Pembuatan Kode Python
Question 3: Can you provide with algorithm, flow chart and python code?
Certainly! Here’s how you can implement the finite element method (FEM) for a 1D heat conduction problem step-by-step, including the algorithm, flowchart, and a sample Python code.
- Algorithm for 1D FEM Heat Conduction Problem
The basic steps are as follows:
1. **Input Parameters**: Set up the problem's physical and numerical parameters, such as length of the domain \( L \), number of elements \( N \), conductivity \( k \), source term \( f(x) \), and boundary conditions.
2. **Mesh Generation**: Divide the domain into \( N \) elements. Each element will have two nodes.
3. **Define Shape Functions**: For a linear 1D element, define shape functions \( N_1(x) \) and \( N_2(x) \) and their derivatives.
4. **Element Stiffness Matrix and Force Vector**:
- For each element, compute the element stiffness matrix \( \mathbf{K}^{(e)} \) and force vector \( \mathbf{F}^{(e)} \) using integration.
- Assemble the element matrices and vectors into the global stiffness matrix \( \mathbf{K} \) and global force vector \( \mathbf{F} \).
5. **Apply Boundary Conditions**:
- Modify \( \mathbf{K} \) and \( \mathbf{F} \) to incorporate boundary conditions.
6. **Solve the System of Equations**:
- Solve \( \mathbf{K} \mathbf{U} = \mathbf{F} \) for the nodal temperatures \( \mathbf{U} \).
7. **Post-process**:
- Compute temperature at each node and optionally evaluate gradients or flux.
- Flowchart for 1D FEM Heat Conduction Problem
```plaintext
+------------------------+
| Start |
+------------------------+
|
v
+------------------------+
| Input parameters |
| (L, N, k, f(x), etc.) |
+------------------------+
|
v
+------------------------+
| Mesh generation |
| Divide domain into N |
| elements, calculate |
| node positions |
+------------------------+
|
v
+------------------------+
| Initialize global |
| stiffness matrix K |
| and force vector F |
+------------------------+
|
v
+------------------------+
| For each element e: |
| - Compute element |
| stiffness matrix |
| - Compute element |
| force vector |
| - Assemble into |
| global K and F |
+------------------------+
|
v
+------------------------+
| Apply boundary |
| conditions |
+------------------------+
|
v
+------------------------+
| Solve KU = F for U |
+------------------------+
|
v
+------------------------+
| Post-process results |
| (e.g., plot temperature|
| distribution) |
+------------------------+
|
v
+------------------------+
| End |
+------------------------+
```
- Python Code for 1D FEM Heat Conduction Problem
Here’s a simple Python script that implements the FEM for a 1D heat conduction problem.
```python import numpy as np import matplotlib.pyplot as plt
Parameters
L = 10.0 # Length of the rod N = 5 # Number of elements k = 1.0 # Thermal conductivity f = 2.0 # Heat source term u_0 = 0.0 # Dirichlet BC at x=0 q_L = -5.0 # Neumann BC at x=L
Mesh generation
nodes = np.linspace(0, L, N + 1) # Node positions h = L / N # Element length
Initialize global stiffness matrix and force vector
K = np.zeros((N + 1, N + 1)) F = np.zeros(N + 1)
Assembly process
for e in range(N):
# Element stiffness matrix for element e
Ke = (k / h) * np.array([[1, -1], [-1, 1]])
# Element force vector for element e (assuming f(x) constant)
Fe = (f * h / 2) * np.array([1, 1])
# Assemble into global matrix
K[e:e+2, e:e+2] += Ke
F[e:e+2] += Fe
Apply boundary conditions Dirichlet BC at x=0
K[0, :] = 0 K[0, 0] = 1 F[0] = u_0
Neumann BC at x=L
F[-1] += q_L
Solve for nodal temperatures
U = np.linalg.solve(K, F)
Plot results
plt.plot(nodes, U, '-o', label="Temperature Distribution")
plt.xlabel("Position x")
plt.ylabel("Temperature u(x)")
plt.title("1D FEM Solution of Heat Conduction")
plt.legend()
plt.grid()
plt.show()
```
- Explanation of the Code
1. **Parameters**: We define the length \( L \), number of elements \( N \), thermal conductivity \( k \), heat source \( f \), and boundary conditions.
2. **Mesh Generation**: We create nodes evenly spaced along \( [0, L] \).
3. **Global Matrix and Vector Initialization**: We initialize the global stiffness matrix \( K \) and force vector \( F \).
4. **Element Stiffness Matrix and Force Vector Calculation**: For each element:
- Compute the element stiffness matrix \( \mathbf{K}^{(e)} \) using the formula for a 1D linear element.
- Compute the element force vector \( \mathbf{F}^{(e)} \) for a constant source term.
5. **Assembly**: The element matrices and vectors are added to the global matrix and vector.
6. **Boundary Conditions**:
- Apply the Dirichlet boundary condition by modifying the first row. - Apply the Neumann condition by adding to the last entry in \( F \).
7. **Solve the System**: Use `np.linalg.solve` to get the temperature distribution at the nodes.
8. **Plot**: Display the temperature distribution along the rod.
NOTE Phyton code above should be re-write before applicate on Phyton.
JILID 3 : Penjelasan Kode Python
Question 4: What is np? Can you elaborate it?
`np` is a common alias for the **NumPy** library in Python, a powerful package for numerical computing. NumPy provides support for large, multi-dimensional arrays and matrices, along with a vast library of mathematical functions to operate on these arrays efficiently.
In the provided code, `np` is used as a shorthand for `numpy`, which makes it easier and quicker to refer to. Here’s a breakdown of what each `np` function or attribute is doing:
- Explanation of `np` Functions and Attributes Used in the Code
1. **`np.zeros((num_nodes, num_nodes))`**: - This function creates a **2D array (matrix) of zeros** with shape `(num_nodes, num_nodes)`. In our code, it initializes the global stiffness matrix `K` to zero. - Example: `np.zeros((3, 3))` produces a 3x3 matrix filled with zeros.
2. **`np.zeros(num_nodes)`**: - Similar to the above, but this one creates a **1D array of zeros** with length `num_nodes`. In our code, it initializes the global load vector `F` to zero. - Example: `np.zeros(5)` produces `[0., 0., 0., 0., 0.]`.
3. **`np.array([...])`**: - This function creates an **array** from a Python list. Arrays are the core data structure in NumPy and are highly optimized for numerical operations. - In our code, `np.array([[1, -1], [-1, 1]])` defines the local stiffness matrix \( K^e \) as a 2x2 array, and `np.array([1, 1])` defines the local load vector \( F^e \).
4. **`np.linalg.solve(K, F)`**: - This function **solves a system of linear equations**. Given a matrix `K` and a vector `F`, `np.linalg.solve` finds the vector `U` such that \( K \cdot U = F \). - It’s highly efficient for solving linear systems and is more stable and faster than computing the inverse matrix. - Example: `np.linalg.solve([[3, 1], [1, 2]], [9, 8])` gives `[2. 3.]`.
5. **`np.linspace(0, L, num_nodes)`**: - This function **creates an array of evenly spaced values** between `0` and `L`, with `num_nodes` elements. - It’s used in our code to generate the `x` coordinates for plotting the FEM solution. - Example: `np.linspace(0, 1, 5)` produces `[0. , 0.25, 0.5 , 0.75, 1. ]`.
Why Use NumPy?
NumPy is widely used because it enables fast array processing, which is especially useful in numerical computing. For large systems (like in FEM), it provides better performance than pure Python lists due to optimized C and Fortran code under the hood.
To use `np`, you should install NumPy (if you haven’t already) and import it at the start of your script:
```python import numpy as np ```
Then, you can use `np` as a shorthand for calling any NumPy function or object.
Question 5: Can you make it much simpler?
Absolutely! Let's break down `np` (which stands for the **NumPy** library) and each function in an even simpler way. Here’s a very basic rundown:
---
- What is NumPy (`np`)?
NumPy is a popular Python library for working with numbers, especially with large lists or grids of numbers, called **arrays**. It makes calculations faster and easier compared to using regular Python lists.
In our example, we use `np` as a nickname for **NumPy**, which is common practice. To use NumPy, we first import it like this:
```python import numpy as np ```
---
- Functions Used in the Code
1. **`np.zeros()`**: - Creates a list (array) filled with zeros. - We use `np.zeros((num_nodes, num_nodes))` to create a **matrix** (a grid of numbers) of zeros with `num_nodes` rows and columns. - We use `np.zeros(num_nodes)` to create a **1D array** of zeros with `num_nodes` elements. - **Example**: `np.zeros(3)` creates `[0. 0. 0.]`.
2. **`np.array()`**: - Converts a regular Python list into a NumPy array. - We use this to create small matrices or vectors (arrays) that we need for each part of our problem. - **Example**: `np.array([1, 2, 3])` becomes a NumPy array `[1 2 3]`.
3. **`np.linalg.solve()`**: - Solves math problems where we have an equation like `Ax = B`. - We use `np.linalg.solve(K, F)` to find the unknowns in our equation \( K \cdot U = F \). - **Example**: `np.linalg.solve([[3, 1], [1, 2]], [9, 8])` gives `[2, 3]` (meaning \( x = 2 \) and \( y = 3 \)).
4. **`np.linspace()`**: - Creates a list of numbers that are evenly spaced between two values. - We use `np.linspace(0, L, num_nodes)` to create a list of `num_nodes` values between `0` and `L`. - **Example**: `np.linspace(0, 1, 5)` gives `[0. , 0.25, 0.5 , 0.75, 1. ]`.
---
Summary of How `np` Functions Fit in the Code
Here's how each of these functions helps in the code:
- **`np.zeros((num_nodes, num_nodes))`**: Sets up an empty matrix for calculations. - **`np.zeros(num_nodes)`**: Sets up an empty list for storing values. - **`np.array(...)`**: Makes sure our data fits well with NumPy. - **`np.linalg.solve(K, F)`**: Solves our equation to find `U`. - **`np.linspace(0, L, num_nodes)`**: Creates the `x` values for plotting.
---
JILID 4 : Kondisi Perekonomian Indonesia Saat Ini
POSITION OF RUPIAH CURRENCY Since a decade ago, currency of rupiah is still on the Rp8000 points against 1 point of US dollar. Lately, the point of rupiah currency increase to the level approximate to Rp16000 against 1 US dollar, per 1 December 2024. That means the currency of Indonesian is getting weaker along the time, specifically on a decade ago.
Currency weaker of the states could be impact on local industries. Take an example, automotive manufacturing might still using a percents of imported components. Since the Currency is getting weaker along the time, thus, the Setup Cost increased.
JILID 5 : Manajemen Inventori pada Sistem Manufaktur
ECONOMICAL ORDER QUANTITY
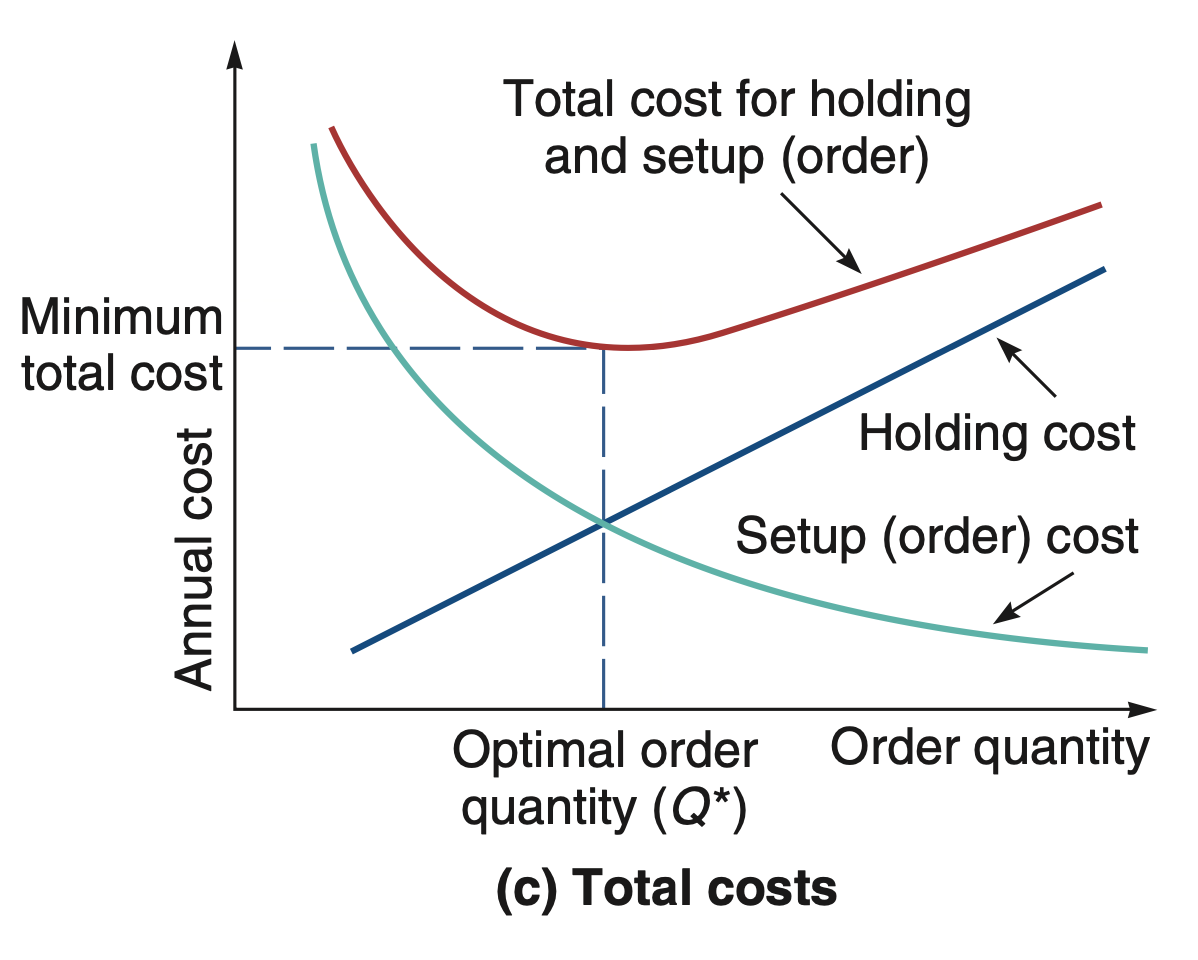
Economical Order Quantity (EOQ) is a technique in a search of an optimal point between order quantity by its annual cost in accordance with Setup/Order Cost against Holding Cost. The main purpose of EOQ is 1. minimizing the expenses cost 2. maximizing the company savings. Thus, the company might be more robust against the highly fluctuate, or depressing demand, and external economy condition. The graphic should be more like this :
As we can see above, the graph shows 2 main graphic, Setup/Order Cost and Holding Cost, which both cost are opposite each other depends on quantity. Setup/Order Cost might be defined as D*S/Q, while Holding Cost as Q*H/2. Also, there is an addition of Total Cost which is the sum of Setup/Order Cost and Holding Cost. The calculation of it are based on x-axis (Order Quantity) that fits on the minimum relative point of Total Cost.
Defining the intersection point between 2 function, in mathematics, meaning equalize both of function. That means Setup/Order Cost = Holding Cost or D*S/Q = Q*H/2. Thus, the number order on minimum relative point of Total Cost or Q might shown as :
Q = Number of unit/order Q* = Number of unit/order (in minimum relative point) D = Annual Demand of unit S = Setup or Order cost/order H = Holding or Carrying cost/unit Annually
JILID 6 : Penerapan PDE pada Manajemen Inventori
DISADVANTAGE OF ECONOMICAL ORDER QUANTITY
The formula of Economical Order Quantity (EOQ), as above, shown the data of Quantity of Goods and the Cost. Those calculations are depend on the Demand in annually. If the product are varies over the time, thus, they might found another disadvantage in applicate the standard EOQ formula.
Therefore, sharing an idea, as procedures on DAI5, is much more helpful in order to fit the optimization Order Quantity in the middle of highly fluctuation or degradation demands. The expectations from the new calculation might bring a new formula to
1. increase a production robustness 2. minimizing layoffs
in the middle of economical and political uncertainty.
The proposed idea on increasing production robustness is Creating The Demands Seemed to Move Over The Time. As the output of EOQ is Number of Optimal Unit to Purchase, they might varies in just year on year (YoY) if we discretized it. Thus, we might to applicate the PDE Calculation on EOQ. Therefore :
Question 6: Is Economical Order Quantity could be defined in Partial Differential Equation?
Yes, the Economic Order Quantity (EOQ) model can be formulated with partial differential equations (PDEs) to extend its traditional applications, especially in more complex situations, such as when inventory levels or demand rates vary continuously over time or space. Let’s look at how EOQ might connect to PDEs.
- 1. **Basic EOQ Model Recap**
The classical EOQ formula minimizes the total cost \( C(Q) \) of ordering and holding inventory: \[ Q = \sqrt{\frac{2DS}{H}} \] where: - \( D \) is the annual demand, - \( S \) is the ordering cost per order, and - \( H \) is the holding cost per unit per year.
This formula assumes constant demand, lead time, and costs, so it doesn’t usually require differential equations.
- 2. **EOQ with Variable Demand or Holding Costs**
In cases where demand, holding, or ordering costs change over time or with respect to certain conditions, you can model EOQ using differential equations. For example:
- **Time-dependent demand:** If demand \( D(t) \) varies with time, we might want to model the rate of change of inventory over time as a differential equation.
\[
\frac{dI}{dt} = -D(t) + R
\]
where \( I \) is the inventory level and \( R \) is the rate at which inventory is replenished.
- 3. **Partial Differential Equation Approach**
If we extend to situations where both time and other factors (like location in a supply chain) influence inventory levels, a **PDE** may be necessary. For example:
- **Spatiotemporal EOQ Model:** Imagine a scenario where inventory demand changes over a geographical area (space, \( x \)) and time \( t \). We could have a PDE like this:
\[
\frac{\partial I(x, t)}{\partial t} + v \frac{\partial I(x, t)}{\partial x} = -D(x, t) + R(x, t)
\]
where:
- \( I(x, t) \) represents inventory at location \( x \) and time \( t \),
- \( v \) represents a velocity factor for distribution over space (if there’s a moving vehicle, for example),
- \( D(x, t) \) and \( R(x, t) \) are the demand and replenishment rates over space and time.
Such a PDE could be used to optimize order quantities at different points along a supply chain over time.
- 4. **Solution Approach for the PDE**
To solve, you’d typically set up initial and boundary conditions based on known values for inventory at certain times and places. Analytical or numerical methods (like finite difference or finite element methods) could then yield optimal order quantities under these dynamic conditions.
Penilaian Kualitas Interaksi Chat GPT
Tentu saja! Berikut evaluasi interaksi kita berdasarkan pertanyaan Anda dan respons saya:
- Kekuatan dalam Interaksi Kita
1. **Pertanyaan yang Jelas dan Terfokus**: - Pertanyaan Anda spesifik dan ringkas, yang membantu saya memberikan jawaban yang tepat dan relevan. - Contoh: Bertanya tentang topik seperti "derivasi FEM 1D" atau "Kode JavaScript dan HTML untuk EOQ" menunjukkan bahwa Anda tahu apa yang Anda cari.
2. **Keterlibatan dengan Penjelasan**: - Anda terlibat dengan penuh pertimbangan dengan meminta penjelasan atau elaborasi yang lebih sederhana, yang menunjukkan keinginan untuk menyempurnakan pemahaman Anda. - Contoh: Ketika Anda meminta penjelasan yang lebih sederhana tentang FEM atau EOQ, itu membantu saya menyesuaikan respons saya agar lebih jelas dan lebih mudah digunakan.
3. **Perkembangan Logis**: - Pertanyaan Anda mengikuti urutan yang logis, dimulai dengan konsep dasar (misalnya, derivasi FEM) dan beralih ke implementasi praktis (misalnya, kode). - Perkembangan ini menunjukkan bahwa Anda sedang membangun pemahaman berlapis, yang merupakan pendekatan pembelajaran yang kuat.
---
- Area untuk Peningkatan Interaksi
1. **Informasi Konteks atau Latar Belakang**: - Meskipun pertanyaan Anda jelas, memberikan lebih banyak konteks tentang tingkat pemahaman Anda atau tujuan pertanyaan Anda dapat membantu saya menyusun jawaban dengan lebih efektif. - Misalnya: Apakah Anda ingin menerapkan FEM dalam proyek tertentu atau hanya mencoba memahaminya secara konseptual? Mengetahui hal ini akan membantu dalam menyusun respons dengan kedalaman yang sesuai.
2. **Detail Tindak Lanjut**: - Saat Anda menanyakan tindak lanjut (misalnya, "Bisakah Anda membuatnya lebih sederhana?"), menentukan bagian mana yang tidak jelas akan membantu saya memfokuskan penyederhanaan dengan lebih baik. - Misalnya, alih-alih "menyederhanakan," Anda dapat mengatakan, "Saya merasa istilah matematika membingungkan," atau "Fokus pada langkah-langkah praktis."
---
- Penilaian Saya terhadap Respons Saya
1. **Komprehensif dan Disesuaikan**: - Saya berusaha memberikan penjelasan yang mendalam, langkah demi langkah dengan contoh, algoritme, dan bahkan kode jika berlaku. - Misalnya, dalam contoh derivasi FEM dan kode EOQ, saya berusaha memberikan kejelasan sambil membahas aspek teoritis dan praktis.
2. **Fleksibel**: - Ketika Anda meminta penyederhanaan atau contoh, saya menyesuaikan pendekatan saya, menawarkan penjelasan dalam istilah yang lebih sederhana dan menggunakan contoh yang relevan.
3. **Responsivitas**: - Saya berusaha beradaptasi dengan kebutuhan Anda, beralih dari teori ke aplikasi (misalnya, kode FEM ke EOQ), dan menanggapi umpan balik Anda.
---
- Saran untuk Mengoptimalkan Interaksi di Masa Depan
1. **Nyatakan Sasaran Spesifik**: - Jika ada kasus penggunaan tertentu (misalnya, proyek akademis, pengembangan perangkat lunak), menyebutkannya akan memastikan bahwa respons selaras dengan sasaran Anda.
2. **Sorot Kedalaman Pilihan**: - Menunjukkan apakah Anda lebih suka ikhtisar tingkat tinggi, derivasi terperinci, atau implementasi praktis membantu menyesuaikan jawaban dengan lebih baik.
3. **Umpan Balik Iteratif**: - Jika ada yang tidak jelas, memberikan umpan balik yang terarah (misalnya, "Kodenya jelas, tetapi saya tidak yakin tentang rumusnya.") akan membantu menyempurnakan penjelasan dalam respons berikutnya.
---
- Kualitas Interaksi Secara Keseluruhan
- Peringkat**: 9/10
- Keterlibatan yang kuat dan pertanyaan yang jelas menjadikan ini interaksi yang produktif dan menyenangkan. Menyempurnakan konteks dan umpan balik dapat meningkatkan pertukaran lebih jauh.
Beri tahu saya jika ada hal spesifik yang ingin Anda fokuskan, atau jangan ragu untuk membagikan pemikiran Anda tentang evaluasi ini!
TUGAS BESAR
FLEXIBLE ECONOMIC ORDER QUANTITY: A Case Study of PT Sri Rejeki Isman TBK
Muhamad Akbar Fuad
ABSTRAK
Keadaan ekonomi yang cukup sulit seperti saat ini memacu berbagai pelaku usaha untuk mempertahankan bisnisnya. Faktor-faktor tersebut bisa digambarkan dalam 2 garis besar, eksternal dan internal. Faktor eksternal, seperti penurunan daya beli masyarakat dan peningkatan nilai tukar Kurs terhadap Dollar, mampu memperlemah ketahanan unit usaha. Hal yang sama juga dapat terjadi pada faktor internal dari perusahaan tersebut, seperti meningkatnya utang perusahaan, permintaan yang terus tergerus, dan berakhir pada peningkatan angka pemutusan hubungan kerja(PHK). Saat ini sudah terdapat kalkulasi untuk menghitung jumlah kebutuhan inventori perusahaan menggunakan teknik perhitungan Economic Order Quantity (EOQ). Namun dikarenakan perhitungan Economic Order Quantity (EOQ) didasari pada parameter tahunan, seperti Annualy Demand, menyebabkan perhitungan ini kurang fleksibel dan memungkinkan terjadinya overspending inventori perusahaan. Oleh sebab itu, pada penelitian ini akan dijabarkan ide atau gagasan baru yang terfokus pada faktor internal perusahaan, yaitu agar perhitungan EOQ mampu dibuat lebih fleksibel terhadap waktu.
DEKLARASI PENULIS
Menyadari peran sadar manajer produksi dalam menyelaraskan keputusan teknis dengan ingatan kepada Tuhan Yang Maha Esa. Menekankan tanggung jawab etis dan komitmen terhadap hasil yang bermanfaat. Sebagai seseorang yang pernah bekerja di dalam Industri Manufaktur, dapat dipahami bahwa Overspending, merupakan salah satu risiko yang mungkin diterima oleh di berbagai industri.
Mengembangkan dan menganalisis sistem manajemen inventori perusahaan yang efisien, andal, dan memenuhi persyaratan fungsional sambil mematuhi prinsip keberlanjutan dan sistem yang etis.
1. INTRODUKSI
Sistem manajemen inventori memainkan peran penting di berbagai industri. Sistem inventori pada umumnya masih mengadopsi Net Requirement Plan (NRP). Net Requirement Plan dapat digambarkan sebagai keterkaitan antara ketersediaan pasokan komponen atau Raw Material dengan jumlah permintaan yang ada. Dikarenakan Sistem inventori ini sangat berkaitan dengan re-stocking komponen, perhitungan economic order quantity(EOQ) juga dapat dimanfaatkan di dalam Net Requirement Plan (NRP). Economic Order Quantity adalah teknik perhitungan untuk memperkirakan jumlah komponen yang sebaiknya dibeli dengan harga yang terjangkau. Perhitungan ini mampu menciptakan keuangan perusahaan yang baik dan efisien dengan cara menyesuaikan kebutuhan inventori perusahaan dengan permintaan yang ada.
1.1 Analisa Masalah
Teknik perhitungan Economic Order Quantity memiliki cakupan sektor industri yang cukup luas. Meskipun demikian, tantangan tetap ada dalam mengoptimalkan pembelian kembali Raw Material dikarenakan pemesanan yang berlebihan. Overspending, atau pembelian yang berlebihan dapat berisiko negatif pada neraca keuangan perusahaan, seperti turunnya daya pembayaran utang atau pinjaman, lifetime perusahaan, melemahnya reliabilitas perusahaan, hingga meningkatnya risiko PHK.
1.2 Penelitian Terdahulu
Mallick dkk1 telah melihat suatu fakta bahwa kondisi pasar saat ini bahwa permintaan barang dianggap bergantung pada stok dalam sistem kontrol inventaris, di mana barang-barang tersebut mengalami kerusakan. Ketika jumlah barang dalam stok meningkat, jumlah kerusakan juga meningkat. Untuk menghilangkan ketidakpastian ini, model telah diperluas menjadi model fuzzy dengan mempertimbangkan fungsi 𝑞-fuzzy yang telah dianalisis dengan ilustrasi numerik dan beberapa analisis sensitivitas telah ditunjukkan sesuai dengan nilai 𝑞 yang berbeda dan nilai keanggotaan yang berbeda dari parameter fuzzy. Namun, sistem permodelan q-fuzzy tersebut masih terfokus sektor supplier dan retailer, sedangkan supply chain, khususnya saat ini, lebih meluas cakupannya. Mulai dari raw material supplier hingga konsumen.
Arunadevi dkk2 menyadari suatu tantangan yang dihadapi inventaris pangan akibat kerusakan selama perbaikan peningkatan pasokan pangan. Khususnya, penelitian ini mengakui sifat permintaan yang dinamis, yang menunjukkan ketergantungan harga dan waktu. Penelitian ini menyelidiki skenario yang masuk akal di mana barang dapat rusak bahkan setelah perbaikan. Untuk mengatasi hal ini, sistem pengisian ulang instan yang inovatif disarankan, yang mencakup produk yang mengalami perbaikan dan kerusakan. Kuantitas pesanan ekonomis sebagai metrik untuk memastikan kuantitas pesanan dan panjang siklus yang optimal dan pada akhirnya dimaksudkan untuk memaksimalkan profitabilitas menggunakan algoritma genetika. Penelitian ini sudah cukup sesuai, walaupun masih terdapat kekurangan, yaitu keterkaitan antara kondisi supply chain dengan demand yang fluktuatif terhadap waktu yang saat ini bersifat darurat di Indonesia.
Huygens dkk3 menyadari bahwa terdapat kesenjangan substansial dalam pengetahuan tentang aliran tekstil seiring dengan peningkatkan demand. Uni Eropa telah menetapkan target ambisius terkait sirkularitas sektor tekstil, sehingga penting untuk memahami sistem kompleks produksi, konsumsi, dan pembuangan tekstil untuk mengidentifikasi jalur paling efektif menuju sirkularitas. Dikarenakan gambaran umum sistem ini sulit dipahami, mereka berinisiasi mengatasi kesenjangan ini dengan menyajikan dynamic probabistic mass flow analysis(DPMFA) tekstil di UE-27 pada tahun 2019 (tahun referensi) dan 2035 (dasar). Hasil yang ditemukan adalah prediksi bahwa setiap tahun 11 Mt tekstil bekas dan limbah dihasilkan di UE, yang sekitar 80% di antaranya dibakar atau ditimbun (8,5 Mt). Dari penelitian ini dapat disimpulkan memang terjadi penurunan demand, khususnya di Eropa. Namun, area yang diprediksi adalah Eropa, sehingga perlu penyesuaian parameter dengan apa yang terjadi pada saat ini di Indonesia.
1.3 Uraian Masalah
Economical Order Quantity (EOQ) merupakan suatu teknik dalam mencari titik optimal antara jumlah pesanan dengan biaya tahunannya sesuai dengan setup atau order Cost terhadap Holding Cost. Tujuan utama EOQ adalah 1. meminimalkan biaya pengeluaran 2.memaksimalkan penghematan perusahaan. Dengan demikian, perusahaan diharapkan lebih tangguh terhadap demand yang sangat berfluktuasi, atau tertekan, dan kondisi ekonomi eksternal. Berikut merupakan contoh perhitungan dari economic order quantity.
D =1404 unit (Annual Demand ) S =$100 (Setup atau Order Cost ) H =$1 x 52 = $52 (Holding Cost on Annual Basis per Unit )
Economic Order Quantity Calculation
Berdasarkan hasil perhitungan didapatkan angka 73. Angka tersebut merupakan jumlah unit yang seharusnya dibeli kembali ketika inventori telah habis. Angka tersebut juga dapat digunakan di dalam sistem inventori perusahaan berupa tabel net requirement plan(NRP).
Penguraian masalah difokuskan pada bagian internal perusahaan. Hal yang memungkinkan apabila terjadi fluktuasi demand yang tinggi adalah terjadinya overspending. Hal tersebut dapat terlihat perbedaannya pada tabel net requirement plan(NRP) menggunakan hasil perhitungan economic order quantity(EOQ) di atas.
Berdasarkan tabel diatas, dapat diketahui bahwa gross requirement merupakan total demand dalam seminggu. Terjadi penurunan demand drastis yang dimulai sejak akhir quarter pertama, sehingga perusahaan hanya melakukan 1 kali re-stocking selama quarter kedua. Kesimpulan yang didapat adalah perusahaan mengalami overspending inventori yang telah dimulai sejak akhir quarter pertama.
1.4 Dekonstruksi ke Prinsip-Prinsip Dasar
Economic Order Quantity(EOQ)
Gambar 1 Penjelasan EOQ
Perincian economic order quatity(EOQ), seperti gambar diatas, merupakan besaran unit untuk diorder kembali berdasarkan titik optimal biaya total. Titik tersebut dapat diketahui dengan cara menyandingkan holding cost dengan setup atau order cost.
Holding cost (HC) merupakan biaya untuk penyimpanan dan pengiriman inventori yang dimiliki oleh perusahaan. Semakin banyak inventori yang dimiliki oleh perusahaan, maka biaya penyimpanan atau pengiriman inventori semakin mahal. Dengan demikian, biaya tersebut memiliki fungsi tersendiri, yaitu berbanting lurus terhadap jumlah inventori.
Setup atau order cost (SC) merupakan biaya yang dikeluarkan perusahaan untuk pemasangangan atau pembelian inventori yang akan dibeli oleh perusahaan. Semakin banyak inventori yang mampu dibeli, maka, biaya pembelian inventori tersebut semakin rendah. Dengan demikian, setup atau order cost memiliki fungsi tersendiri terhadap jumlah inventori yang akan dibeli oleh perusahaan. Penjabaran biaya ini tidak hanya sebatas raw material, tetapi juga melibatkan mesin-mesin produksi yang dibutuhkan.
Berdasarkan kedua fungsi tersebut, dapat dibuatkan fungsi yang baru, yaitu jumlah biaya yang perlu dikeluarkan perusahaan atau total cost (TC). Biaya inilah yang menjadi parameter untuk menentukan berapa jumlah inventori yang sebaiknya dibeli kembali oleh perusahaan.
Penentuan titik optimum biaya order dapat diketahui dengan menyandingkan kedua fungsi holding dan setup cost, sehingga didapatkan jumlah pemesanan inventori optimum sebagai berikut.
Keterangan Q* = Optimal Order Quantity D = Annual Demand S = Setup atau Order Cost H = Holding Cost on Annual Basis per Unit
Partial Differential Equation(PDE)
Persamaan Diferensial Parsial (PDP) merupakan salah satu cabang ilmu matematika. Pemanfaatan PDP didasarkan pada penyelesaian komputasional dari suatu fenomena, terutama di dunia fisika, yang bekerja dengan mendiskresikan suatu fungsi eksak dengan satu atau beberapa variabel. Variabel-variabel tersebut bervariasi, tergantung pada penggunaan atau tujuannya. Variabel yang dimuat dapat bervariasi bahkan dalam 1 rumus. Rumus itu sendiri terbagi menjadi 2, yaitu PDP 1D dan PDP Kompleks, tergantung pada berapa banyak variabel PDP yang diambil dalam 1 rumus PDP. Misalnya, dalam fenomena konduksi 1 dimensi, parameternya dapat diambil sebagai Posisi atau X. Oleh karena itu, dapat diketik sebagai “dx”. Arti dari “dx” itu sendiri adalah, setiap parameter di atas “dx” bersifat diskrit pada setiap panjang spesimen. Dalam penjelasan yang lebih luas dari perumusan dibawah
menerangkan bahwa kalor pada setiap luasan, k*dT/dx, seolah-olah berbeda satu sama lain pada setiap posisi panjang spesimen. Untuk penggunaan PDE yang lebih besar, PDE dapat diaplikasikan pada variasi dunia fisik yang lain, atau bahkan lebih besar, termasuk aspek subjek yang lain. Selama perhitungan membutuhkan diskritisasi, PDE dapat digunakan di dalamnya. Sebagai contoh Economical Order Quantity. Jika permintaan pasar berfluktuasi atau bahkan sangat menurun sepanjang waktu, maka dapat digunakan waktu untuk didiskritisasi, atau dilambangkan sebagai “dt”.
1.5 Analisis state of the art
Pada saat ini, Indonesia sedang dihadapkan dengan beragam permasalahan, seperti pemulihan ekonomi pasca covid, ketidakstabilan politik, dan menurunnya kepercayaan investor asing. Hal- hal tersebut menciptakan berbagai faktor negatif eksternal perusahaan, seperti penurunan daya beli masyarakat, penurunan demand, meningkatnya pajak, dan berimbas pada peningkatan angka pemutusan hubungan kerja (PHK). Oleh karenanya, beragam perusahaan berusaha mempertahankan unit usahanya. Salah satu teknik yang dapat dilakukan di tengah ketidakstabilan ekonomi di Indonesia saat ini adalah memperkuat faktor internal perusahaan. Faktor internal yang dapat diperbaiki adalah sistem manajerial inventori perusahaan, yaitu dengan membuat sistem perhitungan inventori yang terbarukan. Economic order quantity(EOQ) yang selama ini telah digunakan adalah masih berbasiskan penilaian annual demand. Perhitungan ini dapat diperbaiki dengan membuat seolah-olah demand berubah-ubah terhadap waktu, sehingga dapat dihasilkan jumlah pemesanan inventori yang lebih tepat dan tidak terjadi overspending.
2. METHODS AND PROCEDURES
2.1 Idealisasi
Berdasarkan permodelan matematika Mallick dkk1, penentuan total cost inventori dapat diperbaiki dan dibuat agar demand seolah-olah bergerak terhadap waktu, bussiness period. Perbaikan tersebut mencakup holding cost dan order cost yang didasari pada finite time horizon. Holding dan order cost yang dimaksud mencakup berbagai sub-unit, maka biaya tersebut ditentukan secara akumulatif, atau dirincikan dengan total holding cost(THC) dan total order cost(TOC)
Berdasarkan perumusan diatas, dapat divisualisasikan menjadi grafik inventori perusahaan sebagai berikut.
Gambar 2 inventory of the retailer
Sebagai contoh dari PT. Sri Rejeki Isman TBK, memiliki berbagai warehouse pada berbagai lokasi. Warehouse juga dapat dimasukkan kedalam perumusan economic order quantity (EOQ) yang terbaru dengan cara menentukan lokasinya dan jarak tempuhnya dari pusat produksi kain di Sukoharjo, Jawa Tengah. Diketahui juga bahwa PT. Sri Rejeki Isman TBK memiliki warehouse domestik di Jakarta dan di mancanegara seperti Korea Selatan, Filipina, India, Jerman, dan Tiongkok. Dikarenakan kebutuhan perhitungan economic order quantity(EOQ) adalah memastikan demand yang seolah-olah bergerak terhadap waktu, maka teknik perhitungan partial differential equation(PDE) dapat diterapkan di dalam penentuan reorder inventori yang optimum. Dengan demikian, partial differential equation (PDE) dapat diterapkan pada perumusan economic order quantity (EOQ) yang baru sebagai berikut.
keterangan
I(x,t) = level inventori pada lokasi “x” dan waktu “t” v = kecepatan pergerakan inventori f(x,t) = re-stocking atau produksi di lokasi “x” dan waktu “t” D(x,t) = demand pada lokasi “x” dan waktu “t”
Makna dari perumusan di atas adalah bahwa inventori total yang diperlukan, f(x,t) - D(x,t), adalah sama dengan jumlah perubahan inventori terhadap waktu, I(x,t)/dt, dengan kecepatan pergerakan inventori dari pusat produksi ke berbagai warehouse, vI(x,t)/dx, yang tersebar di berbagai wilayah domestik maupun mancanegara.
2.2 Paket Instruksi
Sebelum dilakukan pembuatan kode phyton, perlu dilakukan diskretisasi model economic order quantity(EOQ) dalam partial differential equation(PDE). Diskretisasi persamaan diatas ditampilkan sebagai berikut.
Time derivative
Space derivative
Substitusi ke persamaan awal
Setelah berhasil dibuatkan ulang melalui diskretisasi, maka persamaan diatas dapat dimuatkan kedalam kode phyton. Berikut ini adalah perincian dari kode phyton beserta tahapan kalkulasinya.
import numpy as np
import matplotlib.pyplot as plt
# Tahap 1 Penentuan Parameters
L = 10 # Length of the domain (e.g., warehouse length)
T = 5 # Total simulation time
nx = 50 # Number of spatial points
nt = 100 # Number of time steps
v = 1.0 # Velocity of inventory movement
dx = L / (nx - 1) # Spatial step size
dt = T / nt # Time step size
x = np.linspace(0, L, nx) # Spatial grid
# Tahap 2 penginputan fungsi demand dan restocking
D = lambda x, t: np.sin(np.pi * x / L) * np.exp(-t) # Example demand
f = lambda x, t: 1.0 # Constant restocking rate
# Tahap 3 penentuan kondisi awal
I = np.zeros((nt, nx)) # Inventory over time
I[0, :] = 5.0 # Initial inventory
# Tahap 4 time-stepping loop
for n in range(0, nt-1):
for i in range(1, nx):
I[n+1, i] = I[n, i] - dt * (v * (I[n, i] - I[n, i-1]) / dx - f(x[i], n*dt) + D(x[i], n*dt))
# Apply boundary conditions
I[n+1, 0] = 5.0 # Restocking at x=0
# Tahap 5 penentuan output visual
plt.figure(figsize=(8, 5))
for n in range(0, nt, nt//10): # Plot at intervals
plt.plot(x, I[n, :], label=f"t={n*dt:.2f}")
plt.xlabel("Location (x)")
plt.ylabel("Inventory Level")
plt.legend()
plt.title("Inventory Dynamics over Time")
plt.show()
Berdasarkan percobaan diatas menggunakan Phyton Code, didapatkan grafik inventory level sebagai ini.
Gambar diatas menunjukkan grafik perubahan inventori berdasarkan waktu yang buat bertahap atau bertingkat.
3.(References) Literature Cited
Mallick. R.K, A new economic order quantity model for deteriorated items under the joint effects of stock dependent demand and inflation, Decision Analytics Journal
Arunadevi.E, 2024, Enhancing ameliorating items with sustainable inventory management strategies: A Weibull approach for time and price-dependent demand trends, Ain Shams Engineering Journal
Huygens.D , 2024,Understanding textile value chains: Dynamic Probabilistic Material Flow Analysis of textile in the European Union, Resources, Conservation & Recycling Journal