Difference between revisions of "Wahyu Purnawirawan"
(→1D Element Bar Analysis) |
(→1D Multiphysics Problem Example using Finite Element Analysis (FEM)) |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 94: | Line 94: | ||
• Properties material homogen sepanjang pipa; | • Properties material homogen sepanjang pipa; | ||
| − | • Arah gaya yang bekerja lurus/sejajar dengan sumbu dalam hal ini displacement hanya terjadi pada 1 arah (yaitu pada sumbu x) ; | + | • Arah gaya yang bekerja lurus/sejajar dengan sumbu dalam hal ini displacement hanya terjadi pada 1 arah (yaitu pada sumbu x); |
• Arah gaya tidak membentuk sudut; | • Arah gaya tidak membentuk sudut; | ||
• Beban yang bekerja adalah beban statik. | • Beban yang bekerja adalah beban statik. | ||
| Line 109: | Line 109: | ||
[[File:240911 1D Element Bar Calculix.JPG|600px|thumb|center]] | [[File:240911 1D Element Bar Calculix.JPG|600px|thumb|center]] | ||
| − | Dari simulasi yang dilakukan, dapat dilihat bahwa displacement | + | Dari simulasi yang dilakukan, dapat dilihat bahwa displacement hanya terjadi pada sumbu x sebesar 136,13 mm, dan terbukti bahwa untuk menyelesaikan permasalahan diatas, cukup dengan model 1D sederhana. |
=='''2D Hollow Pipe menggunakan Freecad'''== | =='''2D Hollow Pipe menggunakan Freecad'''== | ||
| Line 224: | Line 224: | ||
'''Kesimpulan: | '''Kesimpulan: | ||
Gambar ini memberikan rangkuman hubungan antara '''tegangan''' dan '''regangan''' dalam tiga dimensi untuk bahan elastis isotropik, dengan memperhitungkan kondisi aksial dan geser. Rumus-rumus tersebut merupakan dasar dari Hukum Hooke dalam bentuk 3D yang digunakan dalam analisis deformasi material, dan dapat disederhanakan untuk kasus '''plane stress''' dan '''plane strain''' sesuai kebutuhan analisis. | Gambar ini memberikan rangkuman hubungan antara '''tegangan''' dan '''regangan''' dalam tiga dimensi untuk bahan elastis isotropik, dengan memperhitungkan kondisi aksial dan geser. Rumus-rumus tersebut merupakan dasar dari Hukum Hooke dalam bentuk 3D yang digunakan dalam analisis deformasi material, dan dapat disederhanakan untuk kasus '''plane stress''' dan '''plane strain''' sesuai kebutuhan analisis. | ||
| + | |||
| + | FEM Multiphysics 1D Temperatur & Displacement | ||
| + | Pertama selesaikan persamaan temperatur distribution, baru kemudian persamaan displacement | ||
| + | dan harus memenuhi persamaan dengan residu yang lebih kecil (Konvergen) | ||
| + | |||
| + | ukuran mesh masuk kedalam bagian Idealisasi (kasar - halus) untuk mempercepat mendapatkan hasil sebagai gambaran | ||
| + | |||
| + | =='''Tugas Besar UTS'''== | ||
| + | |||
| + | Berikut adalah tugas UTS membuat Draft Paper dengan bantuan Chat GPT. Dalam Video ini dibahas bagaimana membuat paper khususnya terkait dengan pipe stress analysis menggunakan Finite Element khususnya dengan metode 1D Element Beam dengan memanfaatkan teknologi Chat GPT untuk memperoleh interaksi mendalam bagaimana framework DAI5 dapat menguraikan permasalahan, sebagiamana dapat dilihat melalui video Youtube berikut | ||
| + | |||
| + | |||
| + | <youtube width="300" height="200"|thumb|center>ugrWGri6QHs</youtube> | ||
| + | |||
| + | |||
| + | =='''1D Multiphysics Problem Example using Finite Element Analysis (FEM)'''== | ||
| + | |||
| + | Berikut adalah contoh soal multifisika 1D di teknik mesin mulai dari persamaan pengatur, turunan persamaan fem, algoritma, diagram alir (flow chart), kode python dan penjelasan detailnya menggunakan framework DAI5, yang terdiri dari I pertama adalah Inisiator (Dr. Ahmad Indra yang mengutip "Saya adalah kesadaran saya"), I kedua adalah Intensi, I ketiga adalah Pemikiran awal tentang masalah, I keempat adalah Idealisasi, dan I kelima adalah Set Instruksi. | ||
| + | |||
| + | '''Langkah-Langkah DAI5 Framework''' | ||
| + | |||
| + | '''1. Initiator''' | ||
| + | Konteks dan Kutipan: Contoh ini berasal dari perspektif pemrakarsa, Dr. Ahmad Indra tentang "Saya adalah kesadaran saya," yang menunjukkan bahwa pendekatan pemecahan masalah harus mengintegrasikan kesadaran setiap fase untuk membangun solusi yang lengkap dan saling berhubungan. | ||
| + | Tujuan Proyek: Memecahkan masalah FEM termal-struktural 1D dengan mempertimbangkan hubungan sadar antara fisika, matematika, dan metode komputasi. | ||
| + | |||
| + | '''2. Intention''' | ||
| + | Tujuan: Maksudnya adalah untuk memahami dan memecahkan bagaimana batang 1D mengembang karena panas melalui penerapan FEM, menggunakan analisis komputasi untuk wawasan praktis. | ||
| + | Aplikasi: Analisis ini berlaku untuk disiplin ilmu teknik yang memerlukan pemodelan suhu dan tegangan pada komponen yang terpapar panas, seperti batang, pipa, atau balok struktural. | ||
| + | |||
| + | '''3. Initial Thinking''' | ||
| + | |||
| + | '''Penyusunan Masalah:''' Kami menganalisis batang 1D dengan panjang | ||
| + | 𝐿 yang mengalami pembangkitan panas internal.'''Kami akan memecahkan''' | ||
| + | |||
| + | • Persamaan Termal: untuk menemukan distribusi suhu. | ||
| + | |||
| + | • Persamaan Struktural: untuk menemukan deformasi akibat ekspansi termal. | ||
| + | |||
| + | '''Persamaan yang Mengatur:''' | ||
| + | |||
| + | Persamaan konduksi panas: | ||
| + | |||
| + | |||
| + | Persamaan struktur dengan regangan termal: | ||
| + | |||
| + | |||
| + | di mana | ||
| + | 𝑘 adalah konduktivitas termal, 𝑇 adalah suhu, 𝑄 adalah pembangkitan panas, 𝐸 adalah modulus Young, 𝑢 adalah perpindahan, dan 𝛼 adalah koefisien ekspansi termal. | ||
| + | |||
| + | '''4. Idealisasi''' | ||
| + | |||
| + | • Penyederhanaan: Sederhanakan batang menjadi elemen-elemen terbatas dan terapkan FEM. | ||
| + | • Langkah-langkah Idealisasi: | ||
| + | • Diskritisasi Domain: Membagi batang menjadi elemen-elemen untuk analisis FEM. | ||
| + | • Analisis Termal: Pecahkan suhu 𝑇 menggunakan FEM. | ||
| + | • Analisis Struktural: Gunakan 𝑇 untuk menghitung regangan termal dan pecahkan perpindahan 𝑢. | ||
| + | • Kondisi Batas: Asumsikan kedua ujung batang tetap atau bebas, tergantung pada pengaturan masalah. | ||
| + | |||
| + | '''5. Set Instruksi (Langkah-langkah Terperinci & Kode Python)''' | ||
| + | |||
| + | 1. Algoritma: | ||
| + | |||
| + | • Pecahkan suhu 𝑇 menggunakan persamaan FEM termal. | ||
| + | • Gunakan 𝑇 untuk menghitung regangan termal dan masukkan ke dalam persamaan FEM struktural. | ||
| + | • Pecahkan perpindahan 𝑢 | ||
| + | • Proses pasca untuk memvisualisasikan suhu dan perpindahan. | ||
| + | |||
| + | 2. Flow Chart: | ||
| + | |||
| + | [Start Program] | ||
| + | | | ||
| + | v | ||
| + | [Initialize Parameters] | ||
| + | - Define material properties | ||
| + | - Set boundary conditions | ||
| + | | | ||
| + | v | ||
| + | [Discretize Domain] | ||
| + | - Divide rod into finite elements | ||
| + | | | ||
| + | v | ||
| + | [Assemble Thermal Matrices] | ||
| + | | | ||
| + | v | ||
| + | [Apply Boundary Conditions (Thermal)] | ||
| + | | | ||
| + | v | ||
| + | [Solve Thermal Problem] | ||
| + | | | ||
| + | v | ||
| + | [Assemble Structural Matrices with Thermal Effects] | ||
| + | | | ||
| + | v | ||
| + | [Apply Boundary Conditions (Structural)] | ||
| + | | | ||
| + | v | ||
| + | [Solve Structural Problem] | ||
| + | | | ||
| + | v | ||
| + | [Post-process Results] | ||
| + | | | ||
| + | v | ||
| + | [End] | ||
| + | |||
| + | 3. Kode Python | ||
| + | |||
| + | import numpy as np | ||
| + | import matplotlib.pyplot as plt | ||
| + | |||
| + | # Material and problem constants | ||
| + | length = 1.0 # length of the rod | ||
| + | num_elements = 10 # number of finite elements | ||
| + | k = 10.0 # thermal conductivity | ||
| + | Q = 5.0 # heat source per unit volume | ||
| + | E = 200.0 # Young's modulus | ||
| + | alpha = 1.2e-5 # thermal expansion coefficient | ||
| + | |||
| + | dx = length / num_elements # element size | ||
| + | nodes = np.linspace(0, length, num_elements + 1) | ||
| + | |||
| + | # Thermal Problem | ||
| + | K_thermal = np.zeros((num_elements + 1, num_elements + 1)) | ||
| + | F_thermal = np.zeros(num_elements + 1) | ||
| + | |||
| + | # Assemble thermal matrix and vector | ||
| + | for i in range(num_elements): | ||
| + | K_thermal[i, i] += k / dx | ||
| + | K_thermal[i, i + 1] -= k / dx | ||
| + | K_thermal[i + 1, i] -= k / dx | ||
| + | K_thermal[i + 1, i + 1] += k / dx | ||
| + | F_thermal[i] += Q * dx / 2 | ||
| + | F_thermal[i + 1] += Q * dx / 2 | ||
| + | |||
| + | # Boundary conditions for thermal problem (T = 0 at boundaries) | ||
| + | K_thermal[0, 0] = K_thermal[-1, -1] = 1 | ||
| + | F_thermal[0] = F_thermal[-1] = 0 | ||
| + | |||
| + | T = np.linalg.solve(K_thermal, F_thermal) | ||
| + | |||
| + | # Structural Problem | ||
| + | K_structural = np.zeros((num_elements + 1, num_elements + 1)) | ||
| + | F_structural = np.zeros(num_elements + 1) | ||
| + | |||
| + | # Assemble structural matrix incorporating thermal expansion | ||
| + | for i in range(num_elements): | ||
| + | K_structural[i, i] += E / dx | ||
| + | K_structural[i, i + 1] -= E / dx | ||
| + | K_structural[i + 1, i] -= E / dx | ||
| + | K_structural[i + 1, i + 1] += E / dx | ||
| + | F_structural[i] -= alpha * E * (T[i] + T[i + 1]) / 2 | ||
| + | F_structural[i + 1] -= alpha * E * (T[i] + T[i + 1]) / 2 | ||
| + | |||
| + | # Boundary conditions for structural problem (u = 0 at boundaries) | ||
| + | K_structural[0, 0] = K_structural[-1, -1] = 1 | ||
| + | F_structural[0] = F_structural[-1] = 0 | ||
| + | |||
| + | u = np.linalg.solve(K_structural, F_structural) | ||
| + | |||
| + | # Post-processing | ||
| + | plt.figure() | ||
| + | plt.plot(nodes, T, label="Temperature (T)") | ||
| + | plt.xlabel("Position along rod") | ||
| + | plt.ylabel("Temperature") | ||
| + | plt.legend() | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | |||
| + | plt.figure() | ||
| + | plt.plot(nodes, u, label="Displacement (u)", color="red") | ||
| + | plt.xlabel("Position along rod") | ||
| + | plt.ylabel("Displacement") | ||
| + | plt.legend() | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | |||
| + | 4. Penjelasan: | ||
| + | |||
| + | • Penyiapan FEM Termal: Membangun matriks K_thermal dan vektor F_thermal untuk masalah konduksi panas. | ||
| + | • Memecahkan Masalah Termal: Menemukan suhu T dengan memecahkan 𝐾𝑡ℎ𝑒𝑟𝑚𝑎𝑙⋅𝑇=𝐹𝑡ℎ𝑒𝑟𝑚𝑎𝑙 | ||
| + | • Penyiapan FEM Struktural: Membangun K_structural dan F_structural untuk masalah struktural, termasuk ekspansi termal. | ||
| + | • Memecahkan Masalah Struktural: Memecahkan perpindahan u berdasarkan regangan yang disebabkan oleh suhu. | ||
Latest revision as of 07:25, 13 November 2024
Assalamu’alaikum, Halo ini adalah homepage saya…
Contents
DAI5 Framework
Berikut adalah tugas pertama pada perkuliahan Finite Element Multiphysics, yaitu menjelaskan pemahaman tentang DAI5 (suatu framework) untuk membantu menguraikan permasalahan dan menemukan solusi dari suatu fenomena /kasus. Agar lebih jelas, silahkan simak video Youtube berikut:
Simple Pipe Stress Modelling
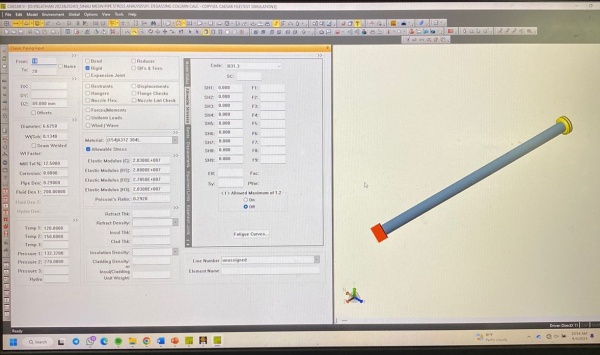
Pada pertemuan kali ini dilakukan latihan simulasi pada struktur pipa sederhana dengan maksud mengetahui displacement dan stress yang terjadi pada struktur tersebut, dengan geometri dan spesifikasi yang diperoleh dari software Caesar II sebagaimana dapat dilihat pada gambar berikut:
DAI5 Framework digunakan untuk menguraikan permasalahan dan membuktikan hasilnya.
1.Intention dilakukan guna menetapkan maksud dan tujuan kita melakukan simulasi yaitu untuk mendapatkan gambaran apakah simulasi menunjukan hasil sesuai dengan yang diharapkan. Kasus kali ialah membuktikan apakah struktur pipa yang mengalami gaya axial akan mengalami displacement terbesar pada titik dimana beban/sumber gaya berasal, sementara stress terbesar akan terjadi pada pangkal pipa ditahan.
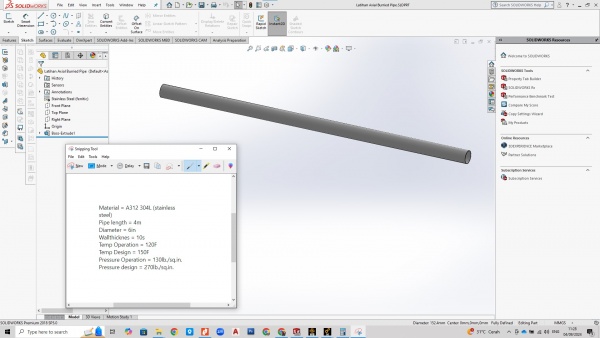
2.Initial Thinking dilakukan dengan menentukan design/bentuk objek berupa geometri dan dimensi Modelling dilakukan menggunakan software solidworks untuk mendapatkan 3D Model.
3.Idealization dilakukan dengan merancang model mendekati dengan kondisi yang sebenarnya, dilengkapi dengan asumsi, gambar dan geometry rancangan serta lingkup/cakupan kondisi.
Pada kasus Axial Buried Pipe Displacement diketahui pipa yang digunakan memiliki panjang 4 meter, diamter 6in, wallthickness 10s, Temperatur operasi 120F, Temperatur design 150F, pressure operation 130lb/sq.in dan pressure design 270/sq.in dengan material yang digunakan ialah A312 304L (stainless steel).
Setelah diperoleh model, langkah selanjutnya ialah membangun asumsi untuk menyederhanakan kasus, diantaranya: • Properties material homogen sepanjang pipa; • Arah gaya yang bekerja lurus/sejajar dengan sumbu/tidak membentuk sudut dsb; • Beban yang bekerja adalah beban statik.
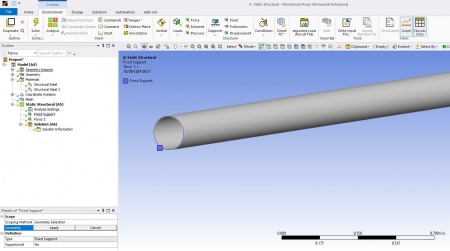
Dari batasan yang telah dibangun sebelumnya, selanjutnya ialah menetapkan beberapa boundary condition, seperti salah satu ujung pipa dalam kondisi ditahan/fix, sementara ujung lainnya mendapatkan beban tekan/tarik, dengan besaran dan arah gaya sejajar sumbu. Modelling dilakukan menggunakan software solidworks untuk mendapatkan 3D Model. Sebagaimana dapat dilihat pada gambar berikut.
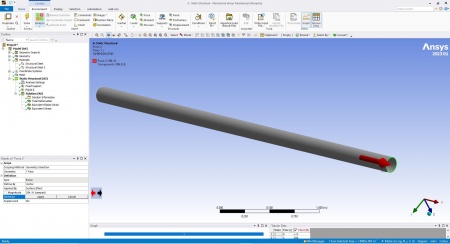
4.Instruction set merupakan langkah-langkah yang harus dilakukan melalui software yang telah dipilih. Dari model yang sudah dibangun, kemudian dilakukan simulasi model menggunakan software Ansys. Tahapan dilakukan sebagaimana yang telah diuraikan pada proses idealization. Salah satu ujung pipa merupakan fixed support, sementara ujung lainnya merupakan titik dimana gaya external bekerja, sebagaimana dapat dilihat pada gambar berikut:
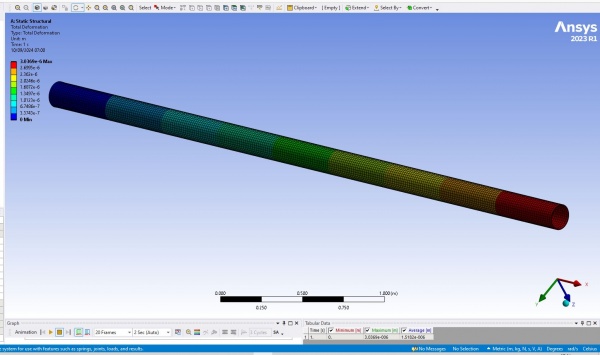
Setelah memasukan berbagai parameter yang telah ditentukan pada tahap initial thinking sebelumnya, program kemudian dapat dijalankan, sehingga didapatkan hasil sebagai berikut.
Dari simulasi yang dilakukan, dapat dilihat bahwa displacement terbesar terjadi pada ujung pipa dimana external force diberikan (3.0369e-006 m). Warna pada pipa menunjukkan besar perpindahan (displacement), di mana warna merah menunjukkan perpindahan terbesar dan biru menunjukkan perpindahan terkecil. Nilai maksimum sekitar 3.0369e-006 m dan nilai minimum sekitar 1.5182e-006 m.
Pertanyaan Apakah posisi displacement terbesar selalu bertolak belakang dengan posisi stress maksimum? apa yang mempengaruhinya dan bagaimana hubungan keduanya?
1D Element Bar Analysis
Pada pertemuan selanjutnya mencoba menggunakan software calculix (Freecad) untuk menyelesaikan kasus sederhana berupa 1D Element Bar. DAI5 Framework digunakan untuk menguraikan permasalahan dan membuktikan hasilnya.
1.Intention dilakukan guna menetapkan maksud dan tujuan kita melakukan simulasi yaitu untuk mendapatkan gambaran apakah simulasi menunjukan hasil sesuai dengan yang diharapkan (pada kesempatan kali ini pipe stress pada model 1D). Pada kasus kali ini dilakukan pembuktian apakah struktur pipa yang mengalami gaya axial akan mengalami displacement terbesar pada titik dimana beban/sumber gaya berasal, sementara stress terbesar akan terjadi pada pangkal pipa ditahan.
2.Initial Thinking dilakukan dengan menentukan design/bentuk objek berupa data-data geometri dan dimensi. Adapun data-data yang diperoleh antara lain:
Panjang Batang = 100 mm
Luas penampang = 150 mm^2
Load = 1000 N
Modulus Young = 200kPa
3.Idealization dilakukan dengan merancang model mendekati dengan kondisi yang sebenarnya, dilengkapi dengan asumsi, gambar dan geometry rancangan serta lingkup/cakupan kondisi. Dari initial thinking yang dilakukan sebelumnya, diperoleh gambaran bahwa untuk menyelesaikan permasalahan cukup dengan menggunakan model 1D Bar.
Setelah diperoleh model, langkah selanjutnya ialah membangun asumsi untuk menyederhanakan kasus, diantaranya:
• Properties material homogen sepanjang pipa; • Arah gaya yang bekerja lurus/sejajar dengan sumbu dalam hal ini displacement hanya terjadi pada 1 arah (yaitu pada sumbu x); • Arah gaya tidak membentuk sudut; • Beban yang bekerja adalah beban statik.
Dari batasan yang telah dibangun sebelumnya, selanjutnya ialah menetapkan beberapa boundary condition, seperti salah satu ujung pipa dalam kondisi ditahan/fix, sementara ujung lainnya mendapatkan beban tekan/tarik, dengan besaran dan arah gaya sejajar sumbu sebesar 1000N. Modelling dilakukan menggunakan software freecad dengan keunggulan aplikasi yang tidak berbayar, tidak memakan memori komputer terlalu besar dan cukup mudah digunakan.
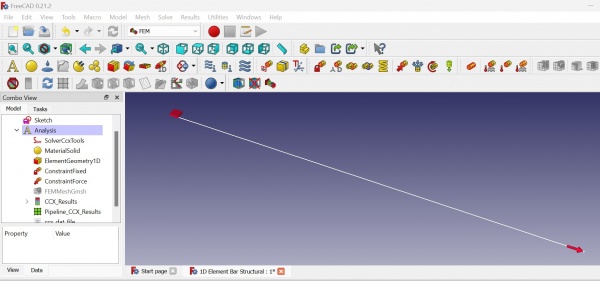
4.Instruction set merupakan langkah-langkah yang harus dilakukan melalui software yang telah dipilih. Dari model yang sudah dibangun, kemudian dilakukan simulasi model menggunakan software Freecad (Calculix). Tahapan dilakukan sebagaimana yang telah diuraikan pada proses idealization. Salah satu ujung pipa merupakan fixed support, sementara ujung lainnya merupakan titik dimana gaya external bekerja, langkah berikutnya yang dilakukan ialah menentukan memasukan mesh (discrete element) dari model/batang yang dibuat. Sebagaimana dapat dilihat pada gambar berikut:
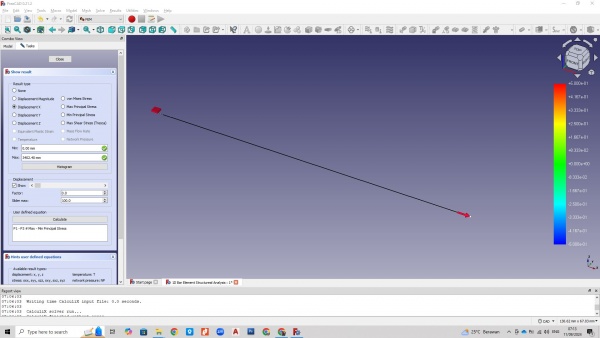
Setelah dimasukan beberapa parameter yang diperlukan pada FreeCAD, langkah seanjutnya ialah menentukan jenis beban yang berlaku pada batang (static) untuk kemudian running Calculix. Hasil dari simulasi (result) dapat diperoleh dan dilihat sebagaimana gambar berikut:
Dari simulasi yang dilakukan, dapat dilihat bahwa displacement hanya terjadi pada sumbu x sebesar 136,13 mm, dan terbukti bahwa untuk menyelesaikan permasalahan diatas, cukup dengan model 1D sederhana.
2D Hollow Pipe menggunakan Freecad
Sharing tentang bagaimana membuat model dan analisis fem sebuah pipa berongga yang ditumpu dikedua sisinya dan mendapatkan beban vertikal menggunakan Freecad. Berikut geometri dari model yang akan dibuat:
Panjang Pipa = 4000mm
Diameter Luar = 168,275mm
Wallthicknes = 3,4mm
Force= 8000N
Catatan Kuliah
Finite Element ialah metode, bukan alat/tool
Kasus yang umum terjadi (realita) displacement bersifat non linear, sehingga perlu disederhanakan (discret > finite)
Matrix dihitung pada nodes > basic variable
Matrix local berlaku hanya untuk 1 node, sementara matrix global berlaku untuk keseluruhan node.
Gaya pada titik, tegangan pada permukaan.
Flux > masuknya volume/masa pada sistem,
Pada region/bagian/descrete tidak akan terjadi overlaping
Prinsipnya ialah kesetimbangan gaya pada nodal, baik pada arah x,y maupun z
Dalam Freecad, tegangan dalam sumbu Z adalah Nol (0) untuk kasus pemodelan pipa Kita perlu melakukan variasi ketebalan buat simulasi 3D element pada pipa, untuk melihat semua tegangan dan displacement ke semua arah. Tegangan pada ketebalan berapa pada arah y tidak sigificant (dimana hal ini dapat di akomodir pada pemodelan 2D Element). Sehingga diperoleh pemahaman, kapan kita menggunakan 2D dan 3D dalam memecahkan permasalahan.
Dalam analisis metode elemen hingga (Finite Element Method/FEM), elemen 1D, 2D, dan 3D digunakan untuk merepresentasikan berbagai jenis objek fisik berdasarkan bentuk dan kompleksitas geometrisnya. Berikut adalah perbedaan antara elemen-elemen tersebut dalam konteks analisis multiphysics:
1. Elemen 1D (Satu Dimensi): Representasi Geometris: Elemen 1D direpresentasikan sebagai garis, yang memiliki panjang tetapi tidak memiliki lebar atau tinggi. Elemen ini sering digunakan untuk memodelkan struktur seperti batang (beam), kolom, kabel, atau elemen tipis panjang lainnya. Aplikasi: Digunakan untuk masalah di mana satu dimensi (panjang) jauh lebih dominan daripada dua dimensi lainnya. Misalnya: Analisis struktur seperti jembatan gantung atau kabel listrik. Analisis getaran pada batang tipis atau kabel. Derajat Kebebasan (DOF): Pada elemen 1D, derajat kebebasan biasanya mencakup perpindahan di sepanjang satu dimensi serta rotasi.
2. Elemen 2D (Dua Dimensi): Representasi Geometris: Elemen 2D berupa bentuk-bentuk seperti segitiga atau kuadrat, yang memiliki panjang dan lebar, tetapi tidak memiliki ketebalan signifikan. Aplikasi: Digunakan untuk memodelkan masalah pada bidang (plane stress atau plane strain), lembaran, atau membran, seperti: Analisis tegangan dan regangan pada lembaran tipis atau pelat. Simulasi fenomena perpindahan panas atau aliran fluida pada permukaan datar. Analisis struktur seperti dinding atau pelat baja. Derajat Kebebasan (DOF): Elemen 2D memungkinkan perpindahan di dua arah (sumbu X dan Y) serta rotasi.
3. Elemen 3D (Tiga Dimensi): Representasi Geometris: Elemen 3D berbentuk padat, seperti tetrahedron, hexahedron (kubus), atau prisma. Elemen ini memiliki panjang, lebar, dan tinggi. Aplikasi: Digunakan untuk memodelkan objek fisik dengan volume, seperti: Struktur padat seperti balok beton atau komponen mekanik. Simulasi fenomena fisika yang kompleks seperti perpindahan panas 3D, aliran fluida dalam ruang tiga dimensi, atau deformasi struktur 3D. Derajat Kebebasan (DOF): Pada elemen 3D, derajat kebebasan mencakup perpindahan di ketiga arah (X, Y, Z) serta rotasi di sekitar ketiga sumbu.
Hukum Hooke dalam 3D (tiga dimensi) yang menghubungkan tegangan (stress) dan regangan (strain) untuk bahan elastis isotropik, baik dalam kondisi aksial maupun geser. Pada gambar ini, terdapat dua kolom utama: Strain di sisi kiri dan Stress di sisi kanan, serta diagram kubus yang menunjukkan tegangan pada berbagai arah. Sebagaimana dapat dilihat pada gambar berikut:
Berikut penjelasan untuk masing-masing bagian:
Axial Strain (Regangan Aksial) Bagian kiri atas menunjukkan rumus untuk regangan aksial (\(\varepsilon_x\), \(\varepsilon_y\), \(\varepsilon_z\)) yang bergantung pada tegangan (\(\sigma_x\), \(\sigma_y\), \(\sigma_z\)) pada ketiga arah utama (x, y, dan z), modulus elastisitas material (E), dan rasio Poisson (**\nu**). Regangan aksial pada setiap arah dihitung menggunakan formula umum Hukum Hooke dalam 3D, yaitu:
\[ \varepsilon_x = \frac{\sigma_x}{E} - \nu \frac{\sigma_y}{E} - \nu \frac{\sigma_z}{E} \] Formulanya serupa untuk arah y dan z. Ini menunjukkan bahwa regangan dalam satu arah tidak hanya bergantung pada tegangan di arah tersebut, tetapi juga dipengaruhi oleh tegangan di arah lainnya melalui efek rasio Poisson.
Shear Strain (Regangan Geser) Bagian tengah bawah menunjukkan rumus untuk **regangan geser** (\(\gamma_{xy}, \gamma_{yz}, \gamma_{zx}\)), yang bergantung pada tegangan geser (\(\tau_{xy}, \tau_{yz}, \tau_{zx}\)) dan **modulus geser** (G). Regangan geser dihitung dengan rumus:
\[ \gamma_{xy} = \frac{\tau_{xy}}{G}, \quad \gamma_{yz} = \frac{\tau_{yz}}{G}, \quad \gamma_{zx} = \frac{\tau_{zx}}{G} \] Ini menunjukkan hubungan antara tegangan geser dan regangan geser melalui modulus geser (G).
Axial Stress (Tegangan Aksial) Bagian kanan atas menunjukkan rumus untuk **tegangan aksial** (\(\sigma_x, \sigma_y, \sigma_z\)) yang dihitung berdasarkan regangan aksial (\(\varepsilon_x, \varepsilon_y, \varepsilon_z\)) dan menggunakan modulus elastisitas (E) serta rasio Poisson (\(\nu\)). Rumus ini menghubungkan regangan dengan tegangan melalui transformasi elastisitas:
\[ \sigma_x = \frac{E}{(1+\nu)(1-2\nu)} \left[ (1-\nu) \varepsilon_x + \nu (\varepsilon_y + \varepsilon_z) \right] \] Formulanya serupa untuk arah y dan z. Ini menunjukkan bahwa tegangan dalam satu arah juga dipengaruhi oleh regangan di arah lain melalui rasio Poisson.
Shear Stress (Tegangan Geser) Bagian kanan bawah menunjukkan rumus untuk tegangan geser (\(\tau_{xy}, \tau_{yz}, \tau_{zx}\)) yang dihitung menggunakan modulus geser (G) dan regangan geser (\(\gamma_{xy}, \gamma_{yz}, \gamma_{zx}\)):
\[ \tau_{xy} = G \gamma_{xy}, \quad \tau_{yz} = G \gamma_{yz}, \quad \tau_{zx} = G \gamma_{zx} \] Rumus ini adalah hubungan dasar antara regangan geser dan tegangan geser.
Transformasi: Plane Stress dan Plane Strain Di bagian tengah atas, ada anotasi tentang transformasi untuk kondisi plane stress dan plane strain, yang merujuk pada penggunaan hukum Hooke dalam kasus-kasus khusus dua dimensi. Dalam plane stress, tegangan di arah z (\(\sigma_z\)) dianggap nol, sementara dalam plane strain, regangan di arah z (\(\varepsilon_z\)) dianggap nol. Transformasi ini membantu menyederhanakan persamaan untuk situasi dua dimensi dalam analisis mekanika material.
Kesimpulan: Gambar ini memberikan rangkuman hubungan antara tegangan dan regangan dalam tiga dimensi untuk bahan elastis isotropik, dengan memperhitungkan kondisi aksial dan geser. Rumus-rumus tersebut merupakan dasar dari Hukum Hooke dalam bentuk 3D yang digunakan dalam analisis deformasi material, dan dapat disederhanakan untuk kasus plane stress dan plane strain sesuai kebutuhan analisis.
FEM Multiphysics 1D Temperatur & Displacement Pertama selesaikan persamaan temperatur distribution, baru kemudian persamaan displacement dan harus memenuhi persamaan dengan residu yang lebih kecil (Konvergen)
ukuran mesh masuk kedalam bagian Idealisasi (kasar - halus) untuk mempercepat mendapatkan hasil sebagai gambaran
Tugas Besar UTS
Berikut adalah tugas UTS membuat Draft Paper dengan bantuan Chat GPT. Dalam Video ini dibahas bagaimana membuat paper khususnya terkait dengan pipe stress analysis menggunakan Finite Element khususnya dengan metode 1D Element Beam dengan memanfaatkan teknologi Chat GPT untuk memperoleh interaksi mendalam bagaimana framework DAI5 dapat menguraikan permasalahan, sebagiamana dapat dilihat melalui video Youtube berikut
1D Multiphysics Problem Example using Finite Element Analysis (FEM)
Berikut adalah contoh soal multifisika 1D di teknik mesin mulai dari persamaan pengatur, turunan persamaan fem, algoritma, diagram alir (flow chart), kode python dan penjelasan detailnya menggunakan framework DAI5, yang terdiri dari I pertama adalah Inisiator (Dr. Ahmad Indra yang mengutip "Saya adalah kesadaran saya"), I kedua adalah Intensi, I ketiga adalah Pemikiran awal tentang masalah, I keempat adalah Idealisasi, dan I kelima adalah Set Instruksi.
Langkah-Langkah DAI5 Framework
1. Initiator Konteks dan Kutipan: Contoh ini berasal dari perspektif pemrakarsa, Dr. Ahmad Indra tentang "Saya adalah kesadaran saya," yang menunjukkan bahwa pendekatan pemecahan masalah harus mengintegrasikan kesadaran setiap fase untuk membangun solusi yang lengkap dan saling berhubungan. Tujuan Proyek: Memecahkan masalah FEM termal-struktural 1D dengan mempertimbangkan hubungan sadar antara fisika, matematika, dan metode komputasi.
2. Intention Tujuan: Maksudnya adalah untuk memahami dan memecahkan bagaimana batang 1D mengembang karena panas melalui penerapan FEM, menggunakan analisis komputasi untuk wawasan praktis. Aplikasi: Analisis ini berlaku untuk disiplin ilmu teknik yang memerlukan pemodelan suhu dan tegangan pada komponen yang terpapar panas, seperti batang, pipa, atau balok struktural.
3. Initial Thinking
Penyusunan Masalah: Kami menganalisis batang 1D dengan panjang 𝐿 yang mengalami pembangkitan panas internal.Kami akan memecahkan
• Persamaan Termal: untuk menemukan distribusi suhu.
• Persamaan Struktural: untuk menemukan deformasi akibat ekspansi termal.
Persamaan yang Mengatur:
Persamaan konduksi panas:
Persamaan struktur dengan regangan termal:
di mana
𝑘 adalah konduktivitas termal, 𝑇 adalah suhu, 𝑄 adalah pembangkitan panas, 𝐸 adalah modulus Young, 𝑢 adalah perpindahan, dan 𝛼 adalah koefisien ekspansi termal.
4. Idealisasi
• Penyederhanaan: Sederhanakan batang menjadi elemen-elemen terbatas dan terapkan FEM. • Langkah-langkah Idealisasi: • Diskritisasi Domain: Membagi batang menjadi elemen-elemen untuk analisis FEM. • Analisis Termal: Pecahkan suhu 𝑇 menggunakan FEM. • Analisis Struktural: Gunakan 𝑇 untuk menghitung regangan termal dan pecahkan perpindahan 𝑢. • Kondisi Batas: Asumsikan kedua ujung batang tetap atau bebas, tergantung pada pengaturan masalah.
5. Set Instruksi (Langkah-langkah Terperinci & Kode Python)
1. Algoritma:
• Pecahkan suhu 𝑇 menggunakan persamaan FEM termal. • Gunakan 𝑇 untuk menghitung regangan termal dan masukkan ke dalam persamaan FEM struktural. • Pecahkan perpindahan 𝑢 • Proses pasca untuk memvisualisasikan suhu dan perpindahan.
2. Flow Chart:
[Start Program]
|
v
[Initialize Parameters]
- Define material properties
- Set boundary conditions
|
v
[Discretize Domain]
- Divide rod into finite elements
|
v
[Assemble Thermal Matrices]
|
v
[Apply Boundary Conditions (Thermal)]
|
v
[Solve Thermal Problem]
|
v
[Assemble Structural Matrices with Thermal Effects]
|
v
[Apply Boundary Conditions (Structural)]
|
v
[Solve Structural Problem]
|
v
[Post-process Results]
|
v
[End]
3. Kode Python
import numpy as np import matplotlib.pyplot as plt
- Material and problem constants
length = 1.0 # length of the rod num_elements = 10 # number of finite elements k = 10.0 # thermal conductivity Q = 5.0 # heat source per unit volume E = 200.0 # Young's modulus alpha = 1.2e-5 # thermal expansion coefficient
dx = length / num_elements # element size nodes = np.linspace(0, length, num_elements + 1)
- Thermal Problem
K_thermal = np.zeros((num_elements + 1, num_elements + 1)) F_thermal = np.zeros(num_elements + 1)
- Assemble thermal matrix and vector
for i in range(num_elements):
K_thermal[i, i] += k / dx K_thermal[i, i + 1] -= k / dx K_thermal[i + 1, i] -= k / dx K_thermal[i + 1, i + 1] += k / dx F_thermal[i] += Q * dx / 2 F_thermal[i + 1] += Q * dx / 2
- Boundary conditions for thermal problem (T = 0 at boundaries)
K_thermal[0, 0] = K_thermal[-1, -1] = 1 F_thermal[0] = F_thermal[-1] = 0
T = np.linalg.solve(K_thermal, F_thermal)
- Structural Problem
K_structural = np.zeros((num_elements + 1, num_elements + 1)) F_structural = np.zeros(num_elements + 1)
- Assemble structural matrix incorporating thermal expansion
for i in range(num_elements):
K_structural[i, i] += E / dx K_structural[i, i + 1] -= E / dx K_structural[i + 1, i] -= E / dx K_structural[i + 1, i + 1] += E / dx F_structural[i] -= alpha * E * (T[i] + T[i + 1]) / 2 F_structural[i + 1] -= alpha * E * (T[i] + T[i + 1]) / 2
- Boundary conditions for structural problem (u = 0 at boundaries)
K_structural[0, 0] = K_structural[-1, -1] = 1 F_structural[0] = F_structural[-1] = 0
u = np.linalg.solve(K_structural, F_structural)
- Post-processing
plt.figure() plt.plot(nodes, T, label="Temperature (T)") plt.xlabel("Position along rod") plt.ylabel("Temperature") plt.legend() plt.grid(True) plt.show()
plt.figure() plt.plot(nodes, u, label="Displacement (u)", color="red") plt.xlabel("Position along rod") plt.ylabel("Displacement") plt.legend() plt.grid(True) plt.show()
4. Penjelasan:
• Penyiapan FEM Termal: Membangun matriks K_thermal dan vektor F_thermal untuk masalah konduksi panas. • Memecahkan Masalah Termal: Menemukan suhu T dengan memecahkan 𝐾𝑡ℎ𝑒𝑟𝑚𝑎𝑙⋅𝑇=𝐹𝑡ℎ𝑒𝑟𝑚𝑎𝑙 • Penyiapan FEM Struktural: Membangun K_structural dan F_structural untuk masalah struktural, termasuk ekspansi termal. • Memecahkan Masalah Struktural: Memecahkan perpindahan u berdasarkan regangan yang disebabkan oleh suhu.