Difference between revisions of "Irwan Haryanto"

From ccitonlinewiki
Jump to: navigation, search
(→‎Trial 2 coding menggunakan phyton untuk menganalisa FEM temperature and thermal stress simulation)
 
(38 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
Tugas 1 FEM tentang DAI5
+
Ini adalah halaman wikipage dari Irwan Haryanto, mahasiswa S2 Teknik Mesin - Perancangan dan Manufaktur Universitas Indonesia
 +
 
 +
=='''Apa itu DAI5 Framework?'''==
 +
 
 +
Di bawah ini merupakan penjelasan singkat tentang DAI5 Framework
  
 
<youtube width="500" height="400">Os_mK0hB-Zc</youtube>
 
<youtube width="500" height="400">Os_mK0hB-Zc</youtube>
  
  
−
Tugas 2 FEM - simple pipe stress static simulation  
+
=='''Simple pipe stress static simulation menggunakan Solidworks'''==
  
 
Simulasi ini menggunakan software Solidworks 2015
 
Simulasi ini menggunakan software Solidworks 2015
Line 22: Line 26:
 
external load : force 1000 N
 
external load : force 1000 N
  
−
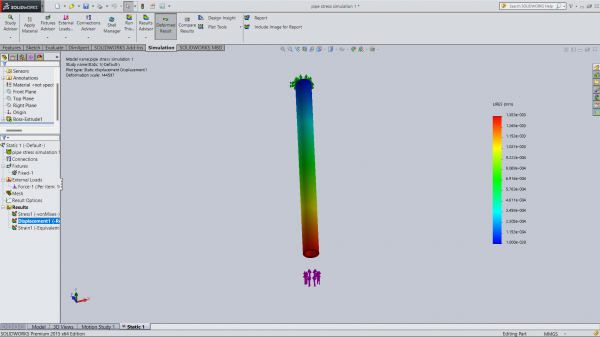
[[File:Screenshot 2024-09-04 114241.png]]
+
[[File:Screenshot 2024-09-04 114241.png|600px]]
  
  
  
 
Dari simulasi yang dilakukan ini, dapat dilihat bahwa displacement terbesar terjadi di ujung pipa dimana external force diberikan. Hasil perpindahan ditampilkan dengan skala deformasi 144597 kali lebih besar dari kondisi asli (untuk memudahkan visualisasi).Warna pada pipa menunjukkan besar perpindahan (displacement), di mana warna merah menunjukkan perpindahan terbesar dan biru menunjukkan perpindahan terkecil. Skala perpindahan (URES) terlihat di sebelah kanan, dengan nilai maksimum sekitar 1.3838e-003 mm dan nilai minimum sekitar 1.000e-030 mm. Dari gambar dapat digunakan untuk memvisualisasikan bagaimana pipa berdeformasi di bawah pengaruh gaya yang diterapkan dalam simulasi tersebut.
 
Dari simulasi yang dilakukan ini, dapat dilihat bahwa displacement terbesar terjadi di ujung pipa dimana external force diberikan. Hasil perpindahan ditampilkan dengan skala deformasi 144597 kali lebih besar dari kondisi asli (untuk memudahkan visualisasi).Warna pada pipa menunjukkan besar perpindahan (displacement), di mana warna merah menunjukkan perpindahan terbesar dan biru menunjukkan perpindahan terkecil. Skala perpindahan (URES) terlihat di sebelah kanan, dengan nilai maksimum sekitar 1.3838e-003 mm dan nilai minimum sekitar 1.000e-030 mm. Dari gambar dapat digunakan untuk memvisualisasikan bagaimana pipa berdeformasi di bawah pengaruh gaya yang diterapkan dalam simulasi tersebut.
 +
 +
=='''Daftar pertanyaan terkait Finite element multiphysic'''==
 +
 +
1. apa itu keseimbangan gaya eksternal dalam pegas ?
 +
 +
 +
 +
 +
=='''Percobaan simulasi 1D element bar dan beam pada Solidworks ELEMENT : BAR'''==
 +
 +
Saya mencoba untuk melakukan simulasi menggunakan software solidworks.
 +
 +
Pada solidworks ini fitur yang ada yaitu 2D Simplified yang memungkinkan untuk melakukan simulasi pada permukaan 2D yang diinginkan saja.
 +
 +
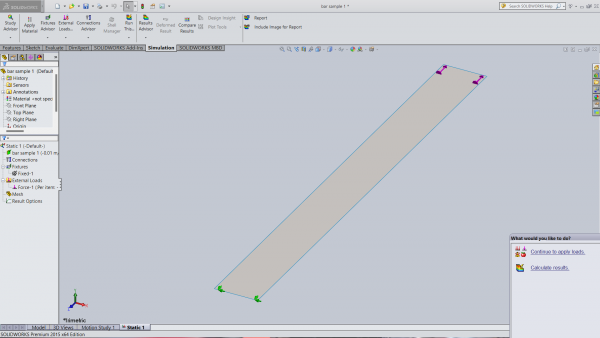
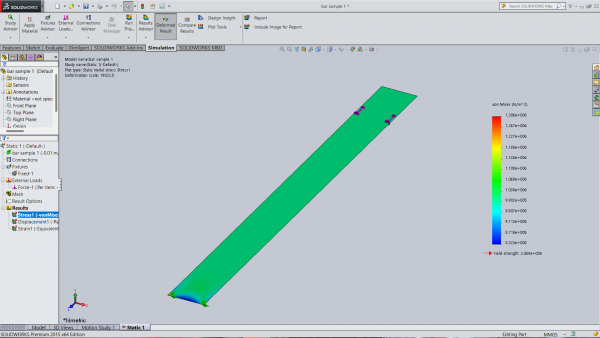
Dimensi bar yang digunakan yaitu 100 mm x 100mm x 1000 mm. Dengan Material SS 304 dan fixed fixtured dengan apply force tarik sebesar 1000 N untuk melihat stress strain dan diplacement pada ujung bar tersebut.
 +
 +
Dokumentasi simulasi ada pada gambar di bawah ini.
 +
 +
[[File:Screenshot 2024-09-17 122643.png|600px]]
 +
 +
[[File:Screenshot 2024-09-17 122911.png|600px]]
 +
 +
 +
=='''Percobaan simulasi 1D element bar pada freecad'''==
 +
 +
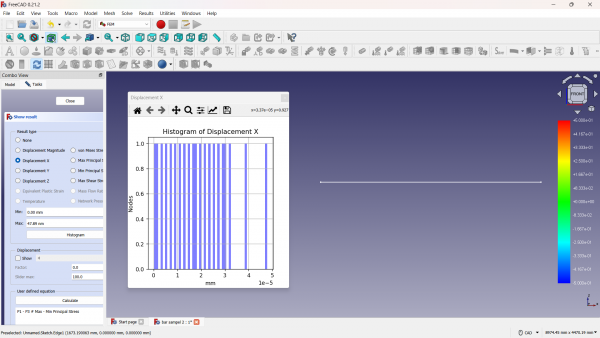
Berikut adalah hasil simulasi dengan parameter sebagai berikut
 +
 +
Material : A312 304L (stainless steel)
 +
 +
Pipe length = 4m
 +
 +
Diameter = 6in
 +
 +
Wallthicknes = 10s
 +
 +
Applied Force : Fix fixtured, dan gaya tekan searah sumbu X
 +
 +
Dokumentasi simulasi ada pada gambar di bawah ini
 +
 +
[[File:bar sampel 1D.png|600px]]
 +
 +
Untuk Penjelasan lebih lanjut dapat dilihat pada video di bawah ini
 +
 +
<youtube width="500" height="400">T97Xp5CrS04</youtube>
 +
 +
 +
 +
=='''Penjelasan singkat Tentang Hooke's law'''==
 +
 +
Hukum Hooke adalah prinsip dasar dalam mekanika yang menyatakan bahwa deformasi suatu benda elastis (seperti pegas atau material padat) berbanding lurus dengan gaya yang diterapkan padanya, selama batas elastisitas material tersebut tidak terlampaui. Persamaan Hukum Hooke adalah:
 +
 +
𝐹=𝑘⋅𝑥
 +
 +
F=k⋅x
 +
 +
F: gaya yang diterapkan (dalam Newton)
 +
k: konstanta pegas (dalam N/m), menggambarkan kekakuan material atau pegas
 +
x: perubahan panjang atau deformasi (dalam meter)
 +
Hukum ini berlaku pada bahan yang bersifat elastis, di mana material akan kembali ke bentuk semula setelah gaya dilepaskan. Hukum Hooke sangat penting dalam desain struktur dan analisis material di bidang teknik mesin.
 +
 +
[[File:hooke law 1.jpg|600px]]
 +
 +
 +
=='''Percobaan simulasi 2D element bar pada freecad'''==
 +
 +
Berikut adalah hasil simulasi dengan parameter sebagai berikut
 +
 +
Material : A312 304L (stainless steel)
 +
 +
Pipe length = 4m
 +
 +
Diameter = 6in
 +
 +
Wallthicknes = 10s
 +
 +
Applied Force : Fix fixtured pada kedua ujung pipa, dan gaya tekan searah sumbu Z pada sebesar 8000 N pada 10 mm permukaan di tengah pipa.
 +
 +
Dokumentasi simulasi ada pada gambar di bawah ini
 +
 +
Dengan Freecad:
 +
 +
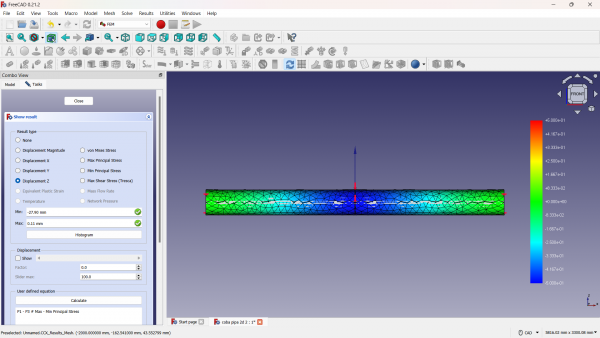
[[File:2D coba pipa 2D-2 freecad 1.png|600px]]
 +
 +
Dengan Paraview:
 +
 +
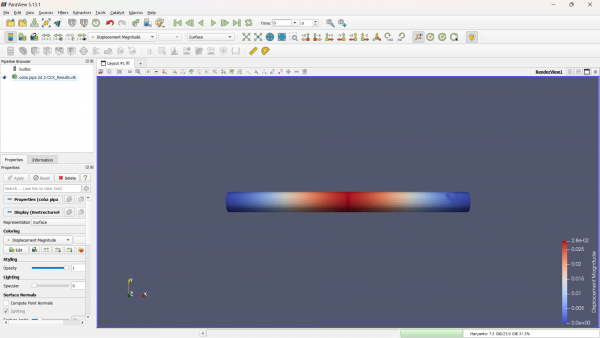
[[File:2D coba pipa 2D-2 paraview 1.png|600px]]
 +
 +
 +
=='''Penerapan DAI5 Framework Dalam Penyelesaian Analisa FEM'''==
 +
 +
Berikut adalah bagaimana peran DAI5 dalam penyelesaian studi kasus analisa FEM
 +
 +
 +
<youtube width="500" height="400">c_a3O_IbVbg</youtube>
 +
 +
 +
'''Apa itu metode Framework DAI5'''
 +
 +
DAI5 merupakan impelementasi dari framework yang disebut dengan Conscious thinking.
 +
 +
Framework ini merupakan framework baru (novel framework) dalam penyelesaian masalah yang dikembangkan dari Framework Computational thinking.
 +
 +
Perangkat Concious thinking yaitu brainware dan heartware
 +
 +
Brainware mengacu pada kemampuan/kapasitas dalam berfikir meliputi kemampuan berpikir analitis, berfikir logis, dan berfikir kreatif.
 +
 +
Heartware dalam conscious thinking ini mengacu pada sila pertama pada dasar Negara Indonesia, yaitu “Ketuhanan yang maha Esa”.
 +
 +
 +
'''Tahapan DAI5'''
 +
 +
1. Intention (langkah awal dimana ditentukan niat, tujuan yang jelas dan simple)
 +
 +
2. Initial Thinking (dilakukan pemahaman secara komprehensif tentang permasalahan yang akan diselesaikan )
 +
 +
3. Idealization (ditujukan agar proses penyelesaian masalah dapat disederhanakan serta dapat diselesaikan secara efektif dengan melakukan suatu pendekatan atau suatu asumsi-asumsi yang dapat dipertanggungjawabkan)
 +
 +
4. Instruction Set (langkah dimana penyelesaian masalah direncanakan dan diimplementasikan melalui serangkaian langkah-langkah yang terstruktur dan sistematis)
 +
 +
'''Bagaimana penerapannya dalam FEM Analysis'''
 +
 +
1. Intention :
 +
 +
Niat yang kuat dan mendalam di hati dan pikiran untuk menyelesaikan permasalahan studi kasus pipa yang diberi beban tertentu dan dengan konfigurasi tertentu
 +
 +
2. Initial Thinking
 +
 +
Pemahaman pada studi kasus pipa secara komprehensif  untuk diselesaikan.
 +
 +
Spesifikasi dan konfigurasi pipa yang akan dianalisa adalah :
 +
 +
Panjang 4000 mm
 +
 +
diamter 6in, wallthickness 10s
 +
 +
Tumpuan fix pada kedua ujung pipa
 +
 +
Fix fixtured pada kedua ujung pipa, dan gaya tekan searah sumbu Z pada sebesar 8000 N pada 10 mm permukaan di tengah pipa.
 +
 +
Material SS 304L
 +
 +
3. Idealization
 +
 +
Dengan penjabaran detail yang sudah dijelaskan pada tahap initial thinking, maka dari itu Analisa FEM bisa dilakukan dengan 2D karena distribusi displacement, plane stress dan plain strain cukup dengan Analisa 2D.
 +
 +
Disamping itu dengan Analisa 2D, komputasi bisa dilakukan dengan lebih sederhana dan dapat menghemat waktu.
 +
 +
4. Instruction Set
 +
 +
Menentukan software apa yang akan digunakan pada Analisa 2D yang telah ditetapkan pada tahap idealization. Saya akan menggunakan software FreeCad dan Paraview.
 +
 +
Freecad dipilih karena opensource, gratis dan bisa melakukan untuk desain 3D dan Analisa FEM baik 1D, 2D dan 3D.
 +
 +
Paraview digunakan untuk membantu visualisasi hasil Analisa yang lebih lengkap.
 +
 +
'''Hasil Akhir Analisa 2D - FreeCad'''
 +
 +
[[File:Hasil 2D Freecad.png|600px]]
 +
 +
'''Hasil Akhir Analisa 2D - Paraview'''
 +
 +
[[File:Hasil 2D Paraview.png|600px]]
 +
 +
'''Kesimpulan'''
 +
 +
1. DAI5 Framework dapat membantu menyelesaikan studi kasus Analisa FEM dengan lebih sederhana namun tidak mengurangi kualitas hasilnya
 +
 +
2. Tahapan DAI5 Framework dapat mengarahkan pengguna dalam menyelesaikan persoalan dengan baik sesuai intention yang telah diyakini.
 +
 +
 +
=='''UTS FEM'''==
 +
 +
<youtube width="500" height="400">kvrH8ZSL9vk</youtube>
 +
 +
referensi : https://chatgpt.com/share/670e8f17-9390-8009-921c-1191148d694a
 +
 +
 +
=='''Trial coding menggunakan phyton untuk menganalisa FEM temperature and thermal stress simulation'''==
 +
 +
import numpy as np
 +
 +
import matplotlib.pyplot as plt
 +
 +
# Constants and Parameters
 +
 +
L = 1.0              # Length of the rod in meters
 +
 +
A = 0.01              # Cross-sectional area in square meters
 +
 +
k = 200              # Thermal conductivity (W/m·K)
 +
 +
E = 210e9            # Young's modulus (Pa)
 +
 +
alpha = 12e-6        # Thermal expansion coefficient (1/K)
 +
 +
T_left = 100          # Temperature at x = 0 (K)
 +
 +
T_right = 200        # Temperature at x = L (K)
 +
 +
n_elements = 10      # Number of elements
 +
 +
 +
# Element length
 +
 +
dx = L / n_elements
 +
 +
 +
# Global stiffness matrix (thermal)
 +
 +
K_T = np.zeros((n_elements + 1, n_elements + 1))
 +
 +
 +
# Assembly of K_T
 +
 +
for i in range(n_elements):
 +
 +
    k_local = (k * A / dx) * np.array([[1, -1], [-1, 1]])
 +
 +
    K_T[i:i+2, i:i+2] += k_local
 +
 +
 +
# Apply boundary conditions
 +
 +
F = np.zeros(n_elements + 1)
 +
 +
F[0] = T_left
 +
 +
F[-1] = T_right
 +
 +
K_T[0, :] = 0
 +
 +
K_T[-1, :] = 0
 +
 +
K_T[0, 0] = 1
 +
 +
K_T[-1, -1] = 1
 +
 +
 +
# Solve for temperature distribution
 +
 +
T = np.linalg.solve(K_T, F)
 +
 +
 +
# Calculate thermal stress
 +
 +
stress = E * alpha * (T - T[0])
 +
 +
 +
# Plotting results
 +
 +
x = np.linspace(0, L, n_elements + 1)
 +
 +
plt.figure(figsize=(12, 6))
 +
 +
plt.subplot(1, 2, 1)
 +
 +
plt.plot(x, T, '-o')
 +
 +
plt.xlabel('Position along the rod (m)')
 +
 +
plt.ylabel('Temperature (K)')
 +
 +
plt.title('Temperature Distribution')
 +
 +
 +
plt.subplot(1, 2, 2)
 +
 +
plt.plot(x, stress, '-o', color='orange')
 +
 +
plt.xlabel('Position along the rod (m)')
 +
 +
plt.ylabel('Stress (Pa)')
 +
 +
plt.title('Thermal Stress Distribution')
 +
 +
plt.tight_layout()
 +
 +
plt.show()
 +
 +
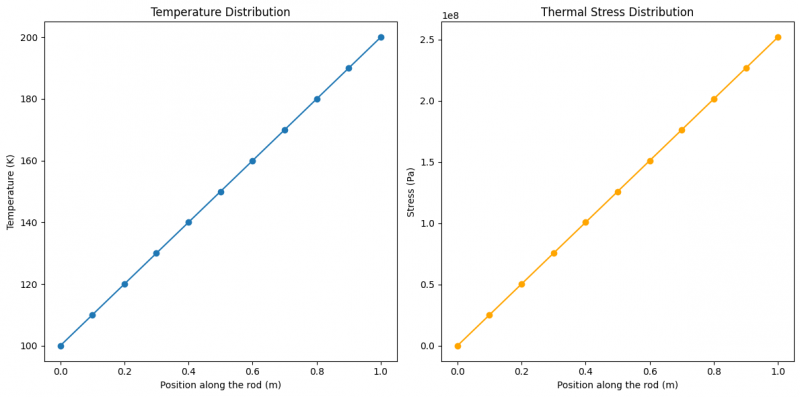
[[File:Temp and thermal stress FEM.png|800px]]
 +
 +
 +
 +
=='''Trial 2 coding menggunakan phyton untuk menganalisa FEM temperature and thermal stress simulation'''==
 +
 +
import numpy as np
 +
 +
import matplotlib.pyplot as plt
 +
 +
 +
# Constants
 +
 +
L = 1.0              # Length of the bar in meters
 +
 +
A = 0.01              # Cross-sectional area in square meters
 +
 +
k = 100              # Thermal conductivity (W/m·K)
 +
 +
E = 210e9            # Young's modulus (Pa)
 +
 +
alpha = 12e-6        # Thermal expansion coefficient (1/K)
 +
 +
P = 1000              # Axial load at the free end (N)
 +
 +
T_left = 300          # Temperature at x = 0 (K)
 +
 +
T_right = 500        # Temperature at x = L (K)
 +
 +
n_elements = 10      # Number of elements
 +
 +
 +
# Element length
 +
 +
dx = L / n_elements
 +
 +
 +
# Global stiffness matrices and force vector
 +
 +
K_T = np.zeros((n_elements + 1, n_elements + 1))  # Thermal stiffness matrix
 +
 +
K_M = np.zeros((n_elements + 1, n_elements + 1))  # Mechanical stiffness matrix
 +
 +
F = np.zeros(n_elements + 1)                      # Force vector for mechanical part
 +
 +
 +
# Assembly for each element
 +
 +
for i in range(n_elements):
 +
 +
    # Thermal element stiffness matrix (1D linear element)
 +
 +
    k_local_T = (k / dx) * np.array([[1, -1], [-1, 1]])
 +
 +
    K_T[i:i+2, i:i+2] += k_local_T
 +
 +
   
 +
    # Mechanical element stiffness matrix
 +
 +
    k_local_M = (E * A / dx) * np.array([[1, -1], [-1, 1]])
 +
 +
    K_M[i:i+2, i:i+2] += k_local_M
 +
 +
 +
# Apply thermal boundary conditions
 +
 +
F_T = np.zeros(n_elements + 1)
 +
 +
F_T[0] = T_left
 +
 +
F_T[-1] = T_right
 +
 +
K_T[0, :] = 0
 +
 +
K_T[-1, :] = 0
 +
 +
K_T[0, 0] = 1
 +
 +
K_T[-1, -1] = 1
 +
 +
 +
# Solve for temperature distribution
 +
 +
T = np.linalg.solve(K_T, F_T)
 +
 +
 +
# Calculate thermal forces for mechanical analysis
 +
 +
thermal_force = E * A * alpha * (T - T[0])
 +
 +
 +
# Apply mechanical boundary conditions (fixed end)
 +
 +
F[-1] = P  # Axial load at free end
 +
 +
 +
F += thermal_force
 +
 +
K_M[0, :] = 0
 +
 +
K_M[0, 0] = 1
 +
 +
F[0] = 0  # Fixed displacement at x = 0
 +
 +
 +
# Solve for displacement
 +
 +
u = np.linalg.solve(K_M, F)
 +
 +
 +
# Calculate stress distribution
 +
 +
stress = E * (np.gradient(u, dx) - alpha * (T - T[0]))
 +
 +
 +
# Plot results
 +
 +
x = np.linspace(0, L, n_elements + 1)
 +
 +
plt.figure(figsize=(12, 6))
 +
 +
plt.subplot(1, 3, 1)
 +
 +
plt.plot(x, T, '-o')
 +
 +
plt.xlabel('Position along the bar (m)')
 +
 +
plt.ylabel('Temperature (K)')
 +
 +
plt.title('Temperature Distribution')
 +
 +
plt.subplot(1, 3, 2)
 +
 +
plt.plot(x, u, '-o')
 +
 +
plt.xlabel('Position along the bar (m)')
 +
 +
plt.ylabel('Displacement (m)')
 +
 +
plt.title('Displacement Distribution')
 +
 +
 +
plt.subplot(1, 3, 3)
 +
 +
plt.plot(x, stress, '-o', color='orange')
 +
 +
plt.xlabel('Position along the bar (m)')
 +
 +
plt.ylabel('Stress (Pa)')
 +
 +
plt.title('Stress Distribution')
 +
 +
plt.tight_layout()
 +
 +
plt.show()
 +
 +
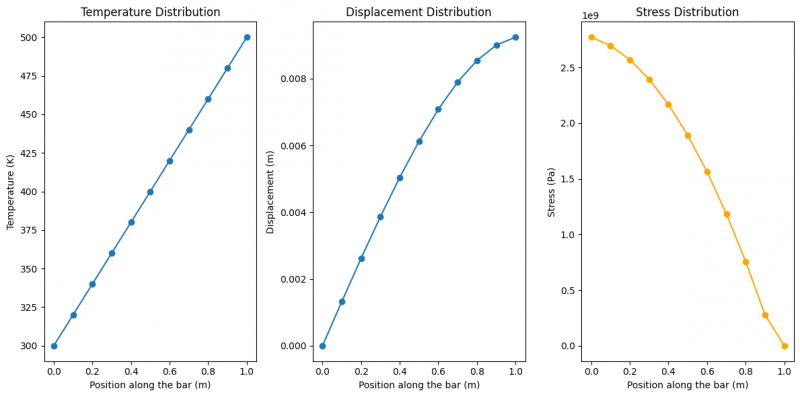
[[File:Temp, displace, stress FEM.png|800 px]]
 +
 +
Berikut adalah flowchart dari phyton code diatas :
 +
 +
[[File:Flow chart tugas FEM stress & thermal.png|200 px]]

Latest revision as of 11:22, 13 November 2024

Ini adalah halaman wikipage dari Irwan Haryanto, mahasiswa S2 Teknik Mesin - Perancangan dan Manufaktur Universitas Indonesia

Apa itu DAI5 Framework?

Di bawah ini merupakan penjelasan singkat tentang DAI5 Framework


Simple pipe stress static simulation menggunakan Solidworks

Simulasi ini menggunakan software Solidworks 2015

parameter yang digunakan yaitu :

dia : 100 mm

thickness : 20 mm

length : 2000 mm

material : AISI 304

fixed geometry

external load : force 1000 N

Screenshot 2024-09-04 114241.png


Dari simulasi yang dilakukan ini, dapat dilihat bahwa displacement terbesar terjadi di ujung pipa dimana external force diberikan. Hasil perpindahan ditampilkan dengan skala deformasi 144597 kali lebih besar dari kondisi asli (untuk memudahkan visualisasi).Warna pada pipa menunjukkan besar perpindahan (displacement), di mana warna merah menunjukkan perpindahan terbesar dan biru menunjukkan perpindahan terkecil. Skala perpindahan (URES) terlihat di sebelah kanan, dengan nilai maksimum sekitar 1.3838e-003 mm dan nilai minimum sekitar 1.000e-030 mm. Dari gambar dapat digunakan untuk memvisualisasikan bagaimana pipa berdeformasi di bawah pengaruh gaya yang diterapkan dalam simulasi tersebut.

Daftar pertanyaan terkait Finite element multiphysic

1. apa itu keseimbangan gaya eksternal dalam pegas ?



Percobaan simulasi 1D element bar dan beam pada Solidworks ELEMENT : BAR

Saya mencoba untuk melakukan simulasi menggunakan software solidworks.

Pada solidworks ini fitur yang ada yaitu 2D Simplified yang memungkinkan untuk melakukan simulasi pada permukaan 2D yang diinginkan saja.

Dimensi bar yang digunakan yaitu 100 mm x 100mm x 1000 mm. Dengan Material SS 304 dan fixed fixtured dengan apply force tarik sebesar 1000 N untuk melihat stress strain dan diplacement pada ujung bar tersebut.

Dokumentasi simulasi ada pada gambar di bawah ini.

Screenshot 2024-09-17 122643.png

Screenshot 2024-09-17 122911.png


Percobaan simulasi 1D element bar pada freecad

Berikut adalah hasil simulasi dengan parameter sebagai berikut

Material : A312 304L (stainless steel)

Pipe length = 4m

Diameter = 6in

Wallthicknes = 10s

Applied Force : Fix fixtured, dan gaya tekan searah sumbu X

Dokumentasi simulasi ada pada gambar di bawah ini

Bar sampel 1D.png

Untuk Penjelasan lebih lanjut dapat dilihat pada video di bawah ini


Penjelasan singkat Tentang Hooke's law

Hukum Hooke adalah prinsip dasar dalam mekanika yang menyatakan bahwa deformasi suatu benda elastis (seperti pegas atau material padat) berbanding lurus dengan gaya yang diterapkan padanya, selama batas elastisitas material tersebut tidak terlampaui. Persamaan Hukum Hooke adalah:

𝐹=𝑘⋅𝑥

F=k⋅x

F: gaya yang diterapkan (dalam Newton) k: konstanta pegas (dalam N/m), menggambarkan kekakuan material atau pegas x: perubahan panjang atau deformasi (dalam meter) Hukum ini berlaku pada bahan yang bersifat elastis, di mana material akan kembali ke bentuk semula setelah gaya dilepaskan. Hukum Hooke sangat penting dalam desain struktur dan analisis material di bidang teknik mesin.

Hooke law 1.jpg


Percobaan simulasi 2D element bar pada freecad

Berikut adalah hasil simulasi dengan parameter sebagai berikut

Material : A312 304L (stainless steel)

Pipe length = 4m

Diameter = 6in

Wallthicknes = 10s

Applied Force : Fix fixtured pada kedua ujung pipa, dan gaya tekan searah sumbu Z pada sebesar 8000 N pada 10 mm permukaan di tengah pipa.

Dokumentasi simulasi ada pada gambar di bawah ini

Dengan Freecad:

2D coba pipa 2D-2 freecad 1.png

Dengan Paraview:

2D coba pipa 2D-2 paraview 1.png


Penerapan DAI5 Framework Dalam Penyelesaian Analisa FEM

Berikut adalah bagaimana peran DAI5 dalam penyelesaian studi kasus analisa FEM



Apa itu metode Framework DAI5

DAI5 merupakan impelementasi dari framework yang disebut dengan Conscious thinking.

Framework ini merupakan framework baru (novel framework) dalam penyelesaian masalah yang dikembangkan dari Framework Computational thinking.

Perangkat Concious thinking yaitu brainware dan heartware

Brainware mengacu pada kemampuan/kapasitas dalam berfikir meliputi kemampuan berpikir analitis, berfikir logis, dan berfikir kreatif.

Heartware dalam conscious thinking ini mengacu pada sila pertama pada dasar Negara Indonesia, yaitu “Ketuhanan yang maha Esa”.


Tahapan DAI5

1. Intention (langkah awal dimana ditentukan niat, tujuan yang jelas dan simple)

2. Initial Thinking (dilakukan pemahaman secara komprehensif tentang permasalahan yang akan diselesaikan )

3. Idealization (ditujukan agar proses penyelesaian masalah dapat disederhanakan serta dapat diselesaikan secara efektif dengan melakukan suatu pendekatan atau suatu asumsi-asumsi yang dapat dipertanggungjawabkan)

4. Instruction Set (langkah dimana penyelesaian masalah direncanakan dan diimplementasikan melalui serangkaian langkah-langkah yang terstruktur dan sistematis)

Bagaimana penerapannya dalam FEM Analysis

1. Intention :

Niat yang kuat dan mendalam di hati dan pikiran untuk menyelesaikan permasalahan studi kasus pipa yang diberi beban tertentu dan dengan konfigurasi tertentu

2. Initial Thinking

Pemahaman pada studi kasus pipa secara komprehensif untuk diselesaikan.

Spesifikasi dan konfigurasi pipa yang akan dianalisa adalah :

Panjang 4000 mm

diamter 6in, wallthickness 10s

Tumpuan fix pada kedua ujung pipa

Fix fixtured pada kedua ujung pipa, dan gaya tekan searah sumbu Z pada sebesar 8000 N pada 10 mm permukaan di tengah pipa.

Material SS 304L

3. Idealization

Dengan penjabaran detail yang sudah dijelaskan pada tahap initial thinking, maka dari itu Analisa FEM bisa dilakukan dengan 2D karena distribusi displacement, plane stress dan plain strain cukup dengan Analisa 2D.

Disamping itu dengan Analisa 2D, komputasi bisa dilakukan dengan lebih sederhana dan dapat menghemat waktu.

4. Instruction Set

Menentukan software apa yang akan digunakan pada Analisa 2D yang telah ditetapkan pada tahap idealization. Saya akan menggunakan software FreeCad dan Paraview.

Freecad dipilih karena opensource, gratis dan bisa melakukan untuk desain 3D dan Analisa FEM baik 1D, 2D dan 3D.

Paraview digunakan untuk membantu visualisasi hasil Analisa yang lebih lengkap.

Hasil Akhir Analisa 2D - FreeCad

Hasil 2D Freecad.png

Hasil Akhir Analisa 2D - Paraview

Hasil 2D Paraview.png

Kesimpulan

1. DAI5 Framework dapat membantu menyelesaikan studi kasus Analisa FEM dengan lebih sederhana namun tidak mengurangi kualitas hasilnya

2. Tahapan DAI5 Framework dapat mengarahkan pengguna dalam menyelesaikan persoalan dengan baik sesuai intention yang telah diyakini.


UTS FEM

referensi : https://chatgpt.com/share/670e8f17-9390-8009-921c-1191148d694a


Trial coding menggunakan phyton untuk menganalisa FEM temperature and thermal stress simulation

import numpy as np

import matplotlib.pyplot as plt

  1. Constants and Parameters

L = 1.0 # Length of the rod in meters

A = 0.01 # Cross-sectional area in square meters

k = 200 # Thermal conductivity (W/m·K)

E = 210e9 # Young's modulus (Pa)

alpha = 12e-6 # Thermal expansion coefficient (1/K)

T_left = 100 # Temperature at x = 0 (K)

T_right = 200 # Temperature at x = L (K)

n_elements = 10 # Number of elements


  1. Element length

dx = L / n_elements


  1. Global stiffness matrix (thermal)

K_T = np.zeros((n_elements + 1, n_elements + 1))


  1. Assembly of K_T

for i in range(n_elements): 

   k_local = (k * A / dx) * np.array([[1, -1], [-1, 1]])

   K_T[i:i+2, i:i+2] += k_local


  1. Apply boundary conditions

F = np.zeros(n_elements + 1)

F[0] = T_left

F[-1] = T_right

K_T[0, :] = 0

K_T[-1, :] = 0

K_T[0, 0] = 1

K_T[-1, -1] = 1


  1. Solve for temperature distribution

T = np.linalg.solve(K_T, F)


  1. Calculate thermal stress

stress = E * alpha * (T - T[0])


  1. Plotting results

x = np.linspace(0, L, n_elements + 1)

plt.figure(figsize=(12, 6))

plt.subplot(1, 2, 1)

plt.plot(x, T, '-o')

plt.xlabel('Position along the rod (m)')

plt.ylabel('Temperature (K)')

plt.title('Temperature Distribution')


plt.subplot(1, 2, 2)

plt.plot(x, stress, '-o', color='orange')

plt.xlabel('Position along the rod (m)')

plt.ylabel('Stress (Pa)')

plt.title('Thermal Stress Distribution')

plt.tight_layout()

plt.show()

Temp and thermal stress FEM.png


Trial 2 coding menggunakan phyton untuk menganalisa FEM temperature and thermal stress simulation

import numpy as np

import matplotlib.pyplot as plt


  1. Constants

L = 1.0 # Length of the bar in meters

A = 0.01 # Cross-sectional area in square meters

k = 100 # Thermal conductivity (W/m·K)

E = 210e9 # Young's modulus (Pa)

alpha = 12e-6 # Thermal expansion coefficient (1/K)

P = 1000 # Axial load at the free end (N)

T_left = 300 # Temperature at x = 0 (K)

T_right = 500 # Temperature at x = L (K)

n_elements = 10 # Number of elements


  1. Element length

dx = L / n_elements


  1. Global stiffness matrices and force vector

K_T = np.zeros((n_elements + 1, n_elements + 1)) # Thermal stiffness matrix

K_M = np.zeros((n_elements + 1, n_elements + 1)) # Mechanical stiffness matrix

F = np.zeros(n_elements + 1) # Force vector for mechanical part


  1. Assembly for each element

for i in range(n_elements): 

   # Thermal element stiffness matrix (1D linear element)

   k_local_T = (k / dx) * np.array([[1, -1], [-1, 1]])

   K_T[i:i+2, i:i+2] += k_local_T



   # Mechanical element stiffness matrix

   k_local_M = (E * A / dx) * np.array([[1, -1], [-1, 1]])

   K_M[i:i+2, i:i+2] += k_local_M


  1. Apply thermal boundary conditions

F_T = np.zeros(n_elements + 1)

F_T[0] = T_left

F_T[-1] = T_right

K_T[0, :] = 0

K_T[-1, :] = 0

K_T[0, 0] = 1

K_T[-1, -1] = 1


  1. Solve for temperature distribution

T = np.linalg.solve(K_T, F_T)


  1. Calculate thermal forces for mechanical analysis

thermal_force = E * A * alpha * (T - T[0])


  1. Apply mechanical boundary conditions (fixed end)

F[-1] = P # Axial load at free end


F += thermal_force

K_M[0, :] = 0

K_M[0, 0] = 1

F[0] = 0 # Fixed displacement at x = 0


  1. Solve for displacement

u = np.linalg.solve(K_M, F)


  1. Calculate stress distribution

stress = E * (np.gradient(u, dx) - alpha * (T - T[0]))


  1. Plot results

x = np.linspace(0, L, n_elements + 1)

plt.figure(figsize=(12, 6))

plt.subplot(1, 3, 1)

plt.plot(x, T, '-o')

plt.xlabel('Position along the bar (m)')

plt.ylabel('Temperature (K)')

plt.title('Temperature Distribution')

plt.subplot(1, 3, 2)

plt.plot(x, u, '-o')

plt.xlabel('Position along the bar (m)')

plt.ylabel('Displacement (m)')

plt.title('Displacement Distribution')


plt.subplot(1, 3, 3)

plt.plot(x, stress, '-o', color='orange')

plt.xlabel('Position along the bar (m)')

plt.ylabel('Stress (Pa)')

plt.title('Stress Distribution')

plt.tight_layout()

plt.show()

Temp, displace, stress FEM.png

Berikut adalah flowchart dari phyton code diatas :

Flow chart tugas FEM stress & thermal.png

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Irwan_Haryanto&oldid=75201"