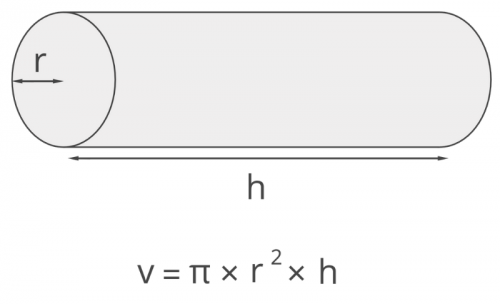Difference between revisions of "Galih Hendra Bhagaskara"
Galih Hendra (talk | contribs) (→Design and Optimization 1 Liter Pressured Hydrogen Storage) |
Galih Hendra (talk | contribs) (→Video Presentasi Study Case) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 144: | Line 144: | ||
'''Total Cost''' | '''Total Cost''' | ||
| − | Material yang digunakan merupakan ASTM A36 yang dimana berdasarkan harga pada e-commerce diperkirakan akan memakan harga Rp | + | Material yang digunakan merupakan ASTM A36 yang dimana berdasarkan harga pada e-commerce diperkirakan akan memakan harga Rp 65.000, lalu ditambah juga dengan jasa machining yang terdiri dari welding, listrik sekitar Rp 200.000. Dibutuhkan juga Nozzle yang berguna untuk memasukan dan mengeluarkan hidrogen dan Pressure gauge untuk mengukur tekanan dalam tangki Sehingga jika ditotal akan mengeluarkan biaya '''Rp 350.000.''' |
| + | |||
| + | |||
| + | ==Video Presentasi Study Case== | ||
| + | |||
| + | [https://www.youtube.com/watch?v=xWmbLnJH6VM Study Case Optimization Hydrogen Tank] | ||
Latest revision as of 04:01, 12 June 2023
Contents
[hide]Hydrogen Storage
Designing and optimizing a 1-liter pressured hydrogen storage system requires consideration of several factors including safety, efficiency, and storage capacity . By addressing these key factors, the design can ensure safe operation, maximize the storage capacity within the given volume, and optimize the system's efficiency. Here are some key points to consider:
1. Material Selection
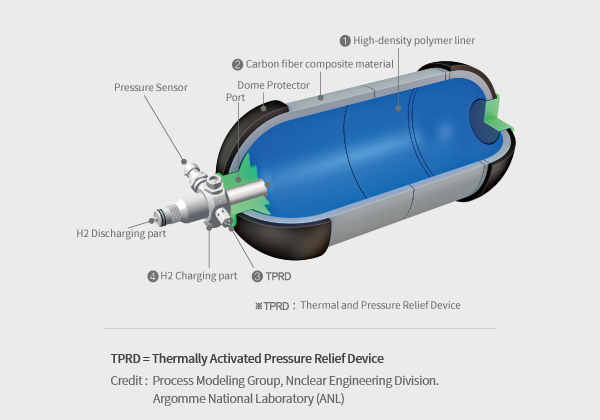
The storage vessel should be made of materials capable of withstanding high-pressure hydrogen storage. The chosen material should have a high strength-to-weight ratio to minimize weight while maintaining safety, Common options include carbon fiber reinforced composite materials or high-strength steel.
2. Vessel Design
The vessel design should consider factors like internal pressure, safety factors, and weight constraints. The shape and configuration of the vessel should distribute stress uniformly, while the wall thickness needs to be optimized for strength and weight requirements. Welding and joint design should ensure structural integrity. Pressure relief mechanisms, such as valves and burst discs, are essential for safety. Proper design considerations can prevent issues like stress concentrations, fatigue cracks, or material degradation over time.
3. Safety Features
Incorporate safety features to ensure reliable and secure hydrogen storage. This may include pressure relief valves, burst disks, and other pressure control mechanisms to prevent over-pressurization. Safety considerations are crucial due to hydrogen's flammability and the potential hazards associated with high-pressure storage.
4. Efficiency and Capacity
Efficiency and capacity are key considerations in designing a 1-liter pressured hydrogen storage system. Maximizing storage capacity involves utilizing advanced adsorption materials and minimizing dead volume. Efficiency is enhanced through materials with low hydrogen permeation, reliable sealing mechanisms, and optimized fill/discharge rates. Energy efficiency can be improved by optimizing insulation and integrating with other system components
5. Testing & Validation
Performance testing evaluates its functionality and ability to store and release hydrogen safely. Burst pressure and pressure cycling tests determine the vessel's structural integrity and durability. Prototyping and field testing provide real-world data for improvements. Thorough testing is essential to identify flaws and meet safety requirements. Collaboration with experts and specialized facilities is recommended for accurate and reliable testing.
Design and Optimization 1 Liter Pressured Hydrogen Storage
Material
Material yang digunakan pada pembuatan hydrogen tank disini yaitu sheet metal ASTM A36 dengan yield strength 248 MPa / 36.000 psi. Lalu kita dapat menghitung allowable stress value = 2/3 x Yield Strength = 165, 3 MPa / 24.000 psi.
Dimension Tank
So that production costs are not too high, a suitable form of hydrogen storage tank is a cylinder with curved ends. If we build a cylinder with an approximate diameter of 10 cm with an internal volume of about 1 liter (1000 cm^3), the height of the tank will be approx.
h = 1000 / (pi x r x r) = 1000 / (3.14 x 5 x 5) = 1000 / 113,04 = 12.73 cm. So the dimensions of the storage tank would have a diameter of 10 cm with a height of around 12.73 cm
To calculate the required wall thickness of the storage vessel in millimeters (mm), we can use the Barlow's formula, assuming a single-welded butt joint and a material with an allowable stress (S) of 24,000 psi and a modulus of elasticity (E) of 0.60.
Given parameters:
Pressure (P) = 8 bar = 116 psi
Radius (R) = 50 mm
Allowable stress (S) = 24,000 psi
Corrosion allowance = 1 mm
First, convert the corrosion allowance from mm to inches:
Corrosion allowance = 1 mm / 25.4 = 0.0394 inches
Python code to calculate the optimized height & radius:
import math
def calculate_surface_area(radius, height):
lateral_area = 2 * math.pi * radius * height
base_area = math.pi * radius**2
return 2 * base_area + lateral_area
def find_optimal_dimensions(volume):
min_surface_area = float('inf')
optimal_radius = 0
optimal_height = 0
for radius in range(1, int(volume**(1/3)) + 1):
height = volume / (math.pi * radius**2)
surface_area = calculate_surface_area(radius, height)
if surface_area < min_surface_area:
min_surface_area = surface_area
optimal_radius = radius
optimal_height = height
return optimal_radius, optimal_height
volume = 1000
radius, height = find_optimal_dimensions(volume)
print(f"Optimal dimensions for a tube with a volume of {volume} cm³:")
print(f"Radius: {radius} cm")
print(f"Height: {height} cm")Dari hasil codingan diatas didapatkan dimensi optimal dari tabung : Radius = 5 cm & Tinggi = 12.73 cm
Next, calculate the required wall thickness (t) using the Barlow's formula:
t = (P * R) / (2 * S + P * E - 1.2 * P)
= (116 psi * 50 mm) / (2 * 24,000 psi + 116 psi * 0.60 - 1.2 * 116 psi)
≈ 2.007 mmTherefore, based on the given parameters and assuming a single-welded butt joint and a material with an allowable stress (S) of 24,000 psi and a modulus of elasticity (E) of 0.60, the required wall thickness of the storage vessel is approximately 2.007 mm.
Surface Area
import math
Height = 8,85
Diameter = 12
thickness = 2.007
def calculate_surface_area(height, diameter, thickness):
height_mm = height
diameter_mm = diameter
thickness_mm = thickness
radius_inner = (diameter_mm / 2) - thickness_mm
radius_outer = diameter_mm / 2
area_inner = 2 * math.pi * radius_inner * height_mm
area_outer = 2 * math.pi * radius_outer * height_mm
area_top_bottom = math.pi * (radius_outer**2 - radius_inner**2)
total_surface_area = area_inner + area_outer + area_top_bottom
return total_surface_area
surface_area = calculate_surface_area(height, diameter, thickness)
print(f"The surface area of the cylindrical vessel is approximately {surface_area:.2f} square millimeters.")Dari hasil codingan diatas didapatkan surface area optimal dari tabung hidrogen:
Luas Area = 618.68 cm^2
Total Cost
Material yang digunakan merupakan ASTM A36 yang dimana berdasarkan harga pada e-commerce diperkirakan akan memakan harga Rp 65.000, lalu ditambah juga dengan jasa machining yang terdiri dari welding, listrik sekitar Rp 200.000. Dibutuhkan juga Nozzle yang berguna untuk memasukan dan mengeluarkan hidrogen dan Pressure gauge untuk mengukur tekanan dalam tangki Sehingga jika ditotal akan mengeluarkan biaya Rp 350.000.