Difference between revisions of "Ariel Ilyasa Fadhilah"
Ariel.ilyasa (talk | contribs) |
Ariel.ilyasa (talk | contribs) (→Video Presentation) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
== Pertemuan 26/05/2023 == | == Pertemuan 26/05/2023 == | ||
| + | Pada pertemuan pertama, Pak DAI membahas mengenai bagaimana penerapan teori consciousness atau bisa disebut dengan kesadaran contoh nya yaitu ketika anda mau masuk kelas yang mendorong anda untuk masuk kelas ialah karna ada absen atau karna kesadaran untuk ingin belajar. Saya mempelajari bahwa Metode numerik banyak digunakan dalam rekayasa untuk memecahkan masalah matematika yang kompleks dan mensimulasikannya di dunia nyata. lalu saat pertemuan pertama juga diberikan subuah soal (x+1)(x-1)/(x-1) = 2, jika kita melakukan substitusi, dalam matematika, pembagian dengan nol tidak terdefinisi, maka diperlukannya consciousness dalam memecah permasalahan tersebut yang kembali lagi bahwa jawabannya akan berbeda-beda tiap individu dikarenakan tingkat consciousness setiap individu juga berbeda serta prinsip dan perspektif yang dipandang. | ||
== Design & Optimization of Pressurized Hydrogen Storage == | == Design & Optimization of Pressurized Hydrogen Storage == | ||
| Line 168: | Line 169: | ||
# Convert wall thickness to meters | # Convert wall thickness to meters | ||
wall_thickness_m = wall_thickness / 1000 | wall_thickness_m = wall_thickness / 1000 | ||
| − | |||
# Calculate the tube's inner radius | # Calculate the tube's inner radius | ||
inner_radius = radius - wall_thickness_m | inner_radius = radius - wall_thickness_m | ||
| − | |||
# Calculate the hoop stress | # Calculate the hoop stress | ||
hoop_stress = (pressure * inner_radius) / wall_thickness_m | hoop_stress = (pressure * inner_radius) / wall_thickness_m | ||
| − | |||
return hoop_stress | return hoop_stress | ||
| − | |||
radius = 6.35 # in cm | radius = 6.35 # in cm | ||
pressure = 205.0 # pressure value in MPa | pressure = 205.0 # pressure value in MPa | ||
| − | |||
# Iterate over different wall thicknesses | # Iterate over different wall thicknesses | ||
current_wall_thickness = 2.55 # in mm | current_wall_thickness = 2.55 # in mm | ||
target_wall_thickness = 8 # in mm | target_wall_thickness = 8 # in mm | ||
increment = 0.5 # increase in wall thickness | increment = 0.5 # increase in wall thickness | ||
| − | |||
while current_wall_thickness <= target_wall_thickness: | while current_wall_thickness <= target_wall_thickness: | ||
hoop_stress = calculate_hoop_stress(radius, current_wall_thickness, pressure) | hoop_stress = calculate_hoop_stress(radius, current_wall_thickness, pressure) | ||
| Line 211: | Line 206: | ||
[[File:Specs1.png]] | [[File:Specs1.png]] | ||
didapatkan hasil pengeluaran sebesar harga barang, yaitu 138.500 rupiah | didapatkan hasil pengeluaran sebesar harga barang, yaitu 138.500 rupiah | ||
| + | |||
| + | == Video Presentation == | ||
| + | [https://www.youtube.com/watch?v=P3EqSdlVjec] | ||
Latest revision as of 22:14, 15 June 2023
Contents
Introduction
Assalamualaikum, Perkenalkan saya Ariel Ilyasa Fadhilah NPM 2106634875 sebagai mahasiswa Teknik Perkapalan Universitas Indonesia
Pertemuan 26/05/2023
Pada pertemuan pertama, Pak DAI membahas mengenai bagaimana penerapan teori consciousness atau bisa disebut dengan kesadaran contoh nya yaitu ketika anda mau masuk kelas yang mendorong anda untuk masuk kelas ialah karna ada absen atau karna kesadaran untuk ingin belajar. Saya mempelajari bahwa Metode numerik banyak digunakan dalam rekayasa untuk memecahkan masalah matematika yang kompleks dan mensimulasikannya di dunia nyata. lalu saat pertemuan pertama juga diberikan subuah soal (x+1)(x-1)/(x-1) = 2, jika kita melakukan substitusi, dalam matematika, pembagian dengan nol tidak terdefinisi, maka diperlukannya consciousness dalam memecah permasalahan tersebut yang kembali lagi bahwa jawabannya akan berbeda-beda tiap individu dikarenakan tingkat consciousness setiap individu juga berbeda serta prinsip dan perspektif yang dipandang.
Design & Optimization of Pressurized Hydrogen Storage
Objective : Design & Optimization of Pressurized Hydrogen Storage
Spesifications :
Capacity : 1 Liter
Pressure Level : 8 bar
Limitation : Cost should not exceed Rp500.000
Week 1 Progress
Before i get to work on this task, For me i consciously think and feel the need to be assisted for this task, I chose the help of an AI platform and ChatGPT was chosen to assist me for this task because of its vast knowledge and the ability to provide me various topics with the explanation that easy to understand. The prompt that i used for this design & optimization of pressurized hydrogen storage was Explain to me comprehensively the factors and processes in designing and optimizing a compact pressurized hydrogen storage with limited cost"
After getting the result, Here's the comprehensive overview of the key considerations:
Storage Method
Pressurized hydrogen storage involves storing hydrogen gas at high pressures. One common method is using high-pressure cylinders made of lightweight, strong materials such as carbon fiber composites or advanced metals like aluminum alloys. Other options include metal hydride storage or cryogenic liquid hydrogen storage, but we'll focus on pressurized storage for this explanation.
Storage Capacity
Determine the required storage capacity in terms of hydrogen mass or volume. This will depend on the application and the desired range or usage time before refueling. Consider factors such as vehicle range, energy demand, or the specific requirements of the system you're designing.
Pressure Level
Select an appropriate pressure level based on safety, storage efficiency, and system requirements. Higher pressures provide greater storage capacity but require stronger materials, leading to increased costs. Common pressure levels for pressurized hydrogen storage range from 350 bar (5,076 psi) to 700 bar (10,152 psi).
Material Selection
Choose materials that can withstand the desired pressure level while minimizing weight and cost. Carbon fiber composite materials are widely used due to their high strength-to-weight ratio, but they can be expensive. Aluminum alloys provide a good balance between strength, weight, and cost.
Tank Design
Optimize the tank design to maximize storage capacity while adhering to safety regulations and minimizing costs. Consider factors such as tank shape, volume, thickness, and the number of tanks required. Advanced design techniques like finite element analysis can help determine the optimal tank shape and thickness distribution.
Safety Measures
Ensure the storage system meets safety standards to prevent leaks, ruptures, or explosions. This involves using certified materials, incorporating pressure relief devices, and designing structural reinforcements to withstand potential accidents. Safety should always be a top priority in hydrogen storage design.
Cost Optimization
Minimize costs by considering factors such as material selection, manufacturing processes, and economies of scale. Explore different manufacturing techniques, such as filament winding or automated fiber placement, to optimize production costs. Additionally, identifying cost-effective suppliers and exploring potential cost-saving innovations can help reduce overall expenses.
System Integration
Ensure seamless integration of the hydrogen storage system with the overall application or infrastructure. Consider factors like system weight, space requirements, and compatibility with other components or systems.
Testing and Certification
Perform rigorous testing to validate the design, ensure safety, and obtain necessary certifications. Test the storage system under various conditions, such as temperature, pressure, and vibration, to evaluate its performance and reliability. Compliance with relevant safety standards and certifications is essential.
Lifecycle Considerations
Consider the environmental impact and overall lifecycle cost of the storage system. Evaluate factors such as recyclability, energy consumption during manufacturing, and end-of-life disposal options to ensure a sustainable and cost-effective solution. Optimizing a compact pressurized hydrogen storage system with limited cost requires a holistic approach, considering technical, safety, economic, and environmental aspects. It is crucial to balance these factors to achieve an efficient and affordable storage solution
Final Project
Requirements
Didalam hal ini pembuatan tabung tabung hidrogen diharapkan memiliki spesifikasi sebagai berikut : volume : 1 liter; tekanan : 8 bar; biaya pembuata : 500.000 rupiah.
Pemilihan Material
Pemilihan material bahan dasar pembuatan tabung hidrogen merupakan kunci utama dalam optimasi tabung hidrogen bertekanan. hal ini didasarkan pada prinsip sifat material sebuah benda tentu saja dipengaruhi oleh material dasar penyusun bendar tersebut. selain itu bahan dasar pembuatan tabung juga mempengaruhi jumlah uang yang dikeluarkan dalam proses pembuatan tabung hidrogen bertekanan. Didalam hal ini stainless steel 316 dipilih menjadi bahan dasar utama karena beberapa alasan diantaranya, material ini dinilai kuat dan memiliki properti yang memadai dalam membuat sebuah tabung hidrogen bertekanan. selain itu harga yang material ini relatif lebih murah untuk properti material yang ditawarkan. dibandingkan dengan jenis material serupa yaitu stainless steel 304, jenis 316 dinilai lebih "bandel" dalam industri karena memiliki kemampaun tahan korosi yang lebih baik. Stainless steel juga merupakan salah satu material yang tidak memiliki permasalahan reaksi dengan hidrogen.
Proses Pembuatan
Didalam membuat tabung ini, dilakukan pembuatan code dengan menentukan rasio perbandingan tinggi dan jari-jari lingkaran sebesar 1:1 dan volume tabung sebesar 1 liter. sehingga daidapatkan hasil sebagai berikut : import math
def calculate_optimal_dimensions(volume):
# Convert volume from liters to cubic centimeters volume_cm3 = volume * 1000 # Calculate the radius using the volume formula radius = (volume_cm3 / math.pi) ** (1/3) # Set the height equal to the radius height = radius return radius, height
# Volume in liters volume = 1
# Calculate the optimal dimensions radius, height = calculate_optimal_dimensions(volume)
# Print the results
print("Optimal Radius: {:.2f} cm".format(radius))
print("Optimal Height: {:.2f} cm".format(height))
Optimal Radius: 6.35 cm Optimal Height: 6.35 cm
Kemudian dilakukan perhitungan ketebalan dinding tabung dengan mempertimbangkan properti material dari stainless steel 316 yaitu, yield value: 2015; tensile strength: 515; elongation: 40; reduction: 69; Hardness: 217 and safety factor 1. kemudian melalui sepsifikasi tersebut dilakukan coding
yield_value = 2015 tensile_strength = 515 elongation = 40 reduction = 69 hardness = 217 safety_factor = 1
def estimate_wall_thickness(yield_value, tensile_strength, safety_factor): wall_thickness = (tensile_strength / (safety_factor * yield_value)) ** 0.5 return wall_thickness
# Estimate the wall thickness estimated_thickness = estimate_wall_thickness(yield_value, tensile_strength, safety_factor)
# Print the result
print("Estimated Wall Thickness: {:.2f} units".format(estimated_thickness))
dengan hasil Estimated Wall Thickness: 2.55 mm
Dengan seluruh data tersebut kemudian dilakukan perhitungan massa tabung
import math
def estimate_tube_mass(radius, height, wall_thickness, density):
volume = math.pi * radius**2 * height
inner_radius = radius - wall_thickness
inner_volume = math.pi * inner_radius**2 * height
tube_volume = volume - inner_volume
mass = tube_volume * density / 1000 # Convert density from kg/m^3 to g/cm^3
return mass
# Parameters
radius = 6.35 # in cm
height = 6.35 # in cm
wall_thickness = 2.55 # in mm
density = 7930 # material density in kg/m^3
# Convert wall thickness to cm
wall_thickness_cm = wall_thickness / 10
# Estimate tube mass
tube_mass = estimate_tube_mass(radius, height, wall_thickness_cm, density)
# Print the result
print("Estimated Tube Mass: {:.2f} grams".format(tube_mass))
didapatkan massa tabung seberat Estimated Tube Mass: 990.77 grams
Iterasi Tekanan
Kemudian untuk memastikan bahwa desain yang dipilih sudah optimum dilakukan iterasi melalui peningkatan ketebalan dinding tabung dengan interval 0.5 mm dimulai dari 2.55 mm hingga 8 mm dengan kode
import math
def calculate_hoop_stress(radius, wall_thickness, pressure):
# Convert wall thickness to meters
wall_thickness_m = wall_thickness / 1000
# Calculate the tube's inner radius
inner_radius = radius - wall_thickness_m
# Calculate the hoop stress
hoop_stress = (pressure * inner_radius) / wall_thickness_m
return hoop_stress
radius = 6.35 # in cm
pressure = 205.0 # pressure value in MPa
# Iterate over different wall thicknesses
current_wall_thickness = 2.55 # in mm
target_wall_thickness = 8 # in mm
increment = 0.5 # increase in wall thickness
while current_wall_thickness <= target_wall_thickness:
hoop_stress = calculate_hoop_stress(radius, current_wall_thickness, pressure)
print("Wall Thickness: {:.2f} mm, Hoop Stress: {:.2f} MPa".format(current_wall_thickness, hoop_stress))
current_wall_thickness += increment
Dan didapatkan Hasil
Wall Thickness: 2.55 mm, Hoop Stress: 1636.42 MPa Wall Thickness: 3.05 mm, Hoop Stress: 1381.82 MPa Wall Thickness: 3.55 mm, Hoop Stress: 1186.26 MPa Wall Thickness: 4.05 mm, Hoop Stress: 1039.79 MPa Wall Thickness: 4.55 mm, Hoop Stress: 922.53 MPa Wall Thickness: 5.05 mm, Hoop Stress: 826.37 MPa Wall Thickness: 5.55 mm, Hoop Stress: 746.31 MPa Wall Thickness: 6.05 mm, Hoop Stress: 678.21 MPa Wall Thickness: 6.55 mm, Hoop Stress: 619.84 MPa Wall Thickness: 7.05 mm, Hoop Stress: 569.38 MPa Wall Thickness: 7.55 mm, Hoop Stress: 525.19 MPa Wall Thickness: 8.05 mm, Hoop Stress: 486.82 MPa
sehingga melalui data tersebut, dapat dilakukan estimasi pengeluaran dengan mempertimbangkan harga barang
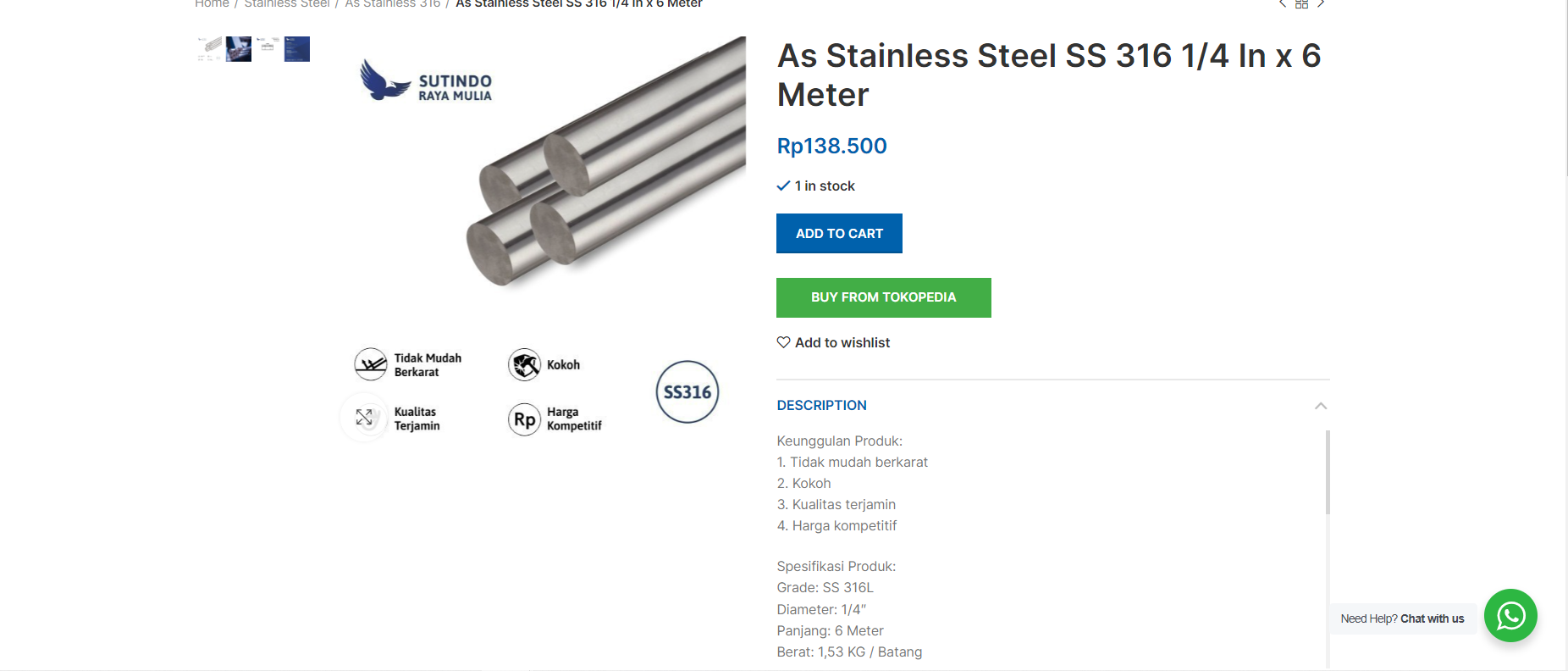 didapatkan hasil pengeluaran sebesar harga barang, yaitu 138.500 rupiah
didapatkan hasil pengeluaran sebesar harga barang, yaitu 138.500 rupiah
