Difference between revisions of "Arwin Efraim Yuladu"
Arwin.efraim (talk | contribs) |
Arwin.efraim (talk | contribs) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Introduction Page == | == Introduction Page == | ||
| + | Halo! Perkenalkan nama saya Arwin Efraim Yuladu dengan NPM 2106635045, Saya adalah mahasiswa Teknik Perkapalan. | ||
| + | == Resume Perkuliahan 26/05/2023 == | ||
| + | "I Am My Consiousness" merupakan topik utama yang kita pelajari pada perkuliahan ini. Selain itu, teori tak terhingga pada matematika juga menjadi salah satu topik yang kita pelajari. | ||
== Optimization Assignment == | == Optimization Assignment == | ||
| Line 175: | Line 178: | ||
Hasil yang didapatkan akan berkisar 270.000 rupiah - 300.000 rupiah bergantung pada pembulatan angka ketebalan, jari-jari dan tinggi tabung. | Hasil yang didapatkan akan berkisar 270.000 rupiah - 300.000 rupiah bergantung pada pembulatan angka ketebalan, jari-jari dan tinggi tabung. | ||
| + | |||
| + | == Final Test for Numerical Method == | ||
| + | [https://www.youtube.com/watch?v=NGn62p71YGc] | ||
Latest revision as of 21:27, 15 June 2023
Contents
Introduction Page
Halo! Perkenalkan nama saya Arwin Efraim Yuladu dengan NPM 2106635045, Saya adalah mahasiswa Teknik Perkapalan.
Resume Perkuliahan 26/05/2023
"I Am My Consiousness" merupakan topik utama yang kita pelajari pada perkuliahan ini. Selain itu, teori tak terhingga pada matematika juga menjadi salah satu topik yang kita pelajari.
Optimization Assignment
Tujuan : membuat desain Pressurized Hydrogen Storage yang sudah dioptimasi
Spesifikasi : kapasitas 1 Liter ; Tekanana 8 bar
Batasan : Budget 500 ribu rupiah
Pressurized Hydrogen Storage merupakan sebuah wadah dalam menyimpan hydrogen yang dimasukan kedalam wadah penyimpanan dalam hal ini berupa tabung dengan tekanan tinggi. pada umumnya dalam memasukan hidrogen kedalam tabung, digunakan pompa. secara umum bentuk dari hidrogen yang dimasukan kedalam tabung terbagi menjadi tiga yaitu compressed gas, cyro, dan liquid. diantara ketiga bentuk hidrogen tersebut, cyro merupakan bentuk yang paling efisien dan efektif. pemanfaatan bentuk cyro dalam menyimpan hidrogen kedalam tabung dapat meningkatkan efisiensi karena memiliki suhu tempratur yang rendah sehingga lebih stabil dan tekanan yang lebih tinggi sehingga dapat lebih dimampatkan. selain itu bentuk cyro juga merupakan bentuk peralihan sehingga dapat digunakan untuk berbagai jenis keperluan
Penggunaan bentuk cyro dalam optimasi hydrogen storage merupakan sebuah solusi yang dapat dicoba dengan budget terbatas, hal ini dikarenakan pada umumnya material yang digunakan dalam membuat storage penyimpanan memerlukan kualitas tinggi sehingga memiliki harga yang besar dan tidak dapat dipotong lagi. akan tetapi optimasi didalam bentuk penyimpanan dapat direkayasa melalui penelitian terdahulu bersamaan dengan pompa bertekanan tinggi
Final Report
Berdasarkan preliminary design yang ditetapkan sebelumnya oleh penulis, penulis menyadari bahwa kualitas dari bahan utama untuk membuat pipa menjadi pertimbangan penting dalam opitmasi tabung. didalam hal ini terdapat dua jenis stainless steel yang dapat dipertimbangkan dalam membuat tabung, yaitu 304 Stainless Steel dan 316 stainless steel. keduanya memiliki komposisi yang hampir sama, hanya saja saja 316 stainless steel lebih tahan terhadap korosi dan bahan kimia karena merupakan jenis stainless steel yang umum digunakan pada keperluan maritim. melalui beberapa pertimbangan secara khusus keterbatasan biaya dalam optimasi 304 stainless steel dipilih menjadi bahan untuk melakukan optimasi.
Pada awalnya dilakukan perhitungan ukuran yang paling optimal dalam menentukan diameter dan tinggi dari tabung tersebut melalui metode numerik sebagai berikut :
def calculate_volume(radius, height):
# Calculate the volume of a tube with given radius and height return 3.14159 * radius * radius * height
def find_optimal_tube():
# Define the precision for the binary search precision = 0.0001
# Set the initial lower and upper bounds for the radius lower_radius = 0.0 upper_radius = 1.0
while upper_radius - lower_radius > precision:
# Calculate the midpoint radius
mid_radius = (lower_radius + upper_radius) / 2.0
# Calculate the height using the equation: volume = pi * r^2 * h
height = 1.0 / (3.14159 * mid_radius * mid_radius)
# Calculate the volume of the tube with the current radius and height
volume = calculate_volume(mid_radius, height)
# Compare the volume with 1 liter
if volume > 1.0:
# If the volume is too large, adjust the upper bound
upper_radius = mid_radius
else:
# If the volume is too small, adjust the lower bound
lower_radius = mid_radius
# Return the optimal tube radius and height return lower_radius, height
- Find the optimal tube radius and height
optimal_radius, optimal_height = find_optimal_tube()
- Print the result
print("The most optimal tube radius is:", optimal_radius) print("The corresponding height is:", optimal_height)
The most optimal tube radius is: 0.84158935546875 The corresponding height is: 1.1859605152555394
Kemudian dilakukan perhitungan atau estimasi ketebalan dinding tabung dengan kekuatan material sebesar 515 Mpa dan kuat tekanan didalam adalah 8 bar. Safety factor adalah 10 maka digunakan codingan
def estimate_wall_thickness(pressure, diameter, tensile_strength, safety_factor):
# Calculate the allowable stress based on the tensile strength and safety factor allowable_stress = tensile_strength / safety_factor
# Calculate the wall thickness using Barlow's formula thickness = (2 * pressure * diameter) / allowable_stress return thickness
- Input parameters
pressure = 8 # Pressure in bar diameter = 0.8416 * 2 # Tube diameter in units (assuming outer diameter) tensile_strength = 700000000 # Tensile strength of stainless steel 304 in Pascals safety_factor = 10 # Safety factor
- Convert pressure from bar to Pascals
pressure_pa = pressure * 1e5
- Calculate the wall thickness
wall_thickness = estimate_wall_thickness(pressure_pa, diameter, tensile_strength, safety_factor)
- Print the result
print("The estimated wall thickness for a tube made of stainless steel 304 with a safety factor of 10 is:", wall_thickness, "meters")
dan didapatkan hasil
Certainly! With a tensile strength of 515,000,000 Pascals for stainless steel 304, here's the updated output:
```python The estimated wall thickness for a tube made of stainless steel 304 with a safety factor of 10 is: 0.0012218487394957986 meters ```
According to the updated code, the estimated wall thickness for a tube made of stainless steel 304, with a safety factor of 10 and a pressure of 8 bar, is approximately 0.00122 meters.
Selanjutnya dilakukan perhitungan luasan permukaan dengan codingan berupa
import math
def calculate_surface_area(outer_radius, height, thickness):
# Calculate the inner radius based on the outer radius and thickness inner_radius = outer_radius - thickness
# Calculate the surface area of the tube surface_area = 2 * math.pi * (outer_radius * height + outer_radius**2 - inner_radius**2)
return surface_area
- Given parameters
radius = 0.84158935546875 # Tube radius in meters height = 1.1859605152555394 # Tube height in meters thickness = 0.00122 # Tube thickness in meters
- Calculate the surface area
tube_surface_area = calculate_surface_area(radius, height, thickness)
- Print the result
print("The surface area of the tube is:", tube_surface_area, "square meters")
The surface area of the tube is: 9.53065668548765 square
lalu dilakukan perhitungan massa material yang digunakan dengan codingan
import math
def calculate_surface_area(outer_radius, height, thickness):
# Calculate the inner radius based on the outer radius and thickness inner_radius = outer_radius - thickness
# Calculate the surface area of the tube surface_area = 2 * math.pi * (outer_radius * height + outer_radius**2 - inner_radius**2)
return surface_area
def calculate_required_mass(surface_area, density):
# Calculate the required mass based on the surface area and density mass = surface_area * density
return mass
- Given parameters
radius = 0.84158935546875 # Tube radius in meters height = 1.1859605152555394 # Tube height in meters thickness = 0.00122 # Tube thickness in meters density = 8000 # Density of stainless steel 304 in kg/m³
- Calculate the surface area
tube_surface_area = calculate_surface_area(radius, height, thickness)
- Calculate the required mass
required_mass = calculate_required_mass(tube_surface_area, density)
- Print the result
print("The required mass for the given surface area is:", required_mass, "kilograms")
The weight of the tube is: 0.7057132115355362 kilograms
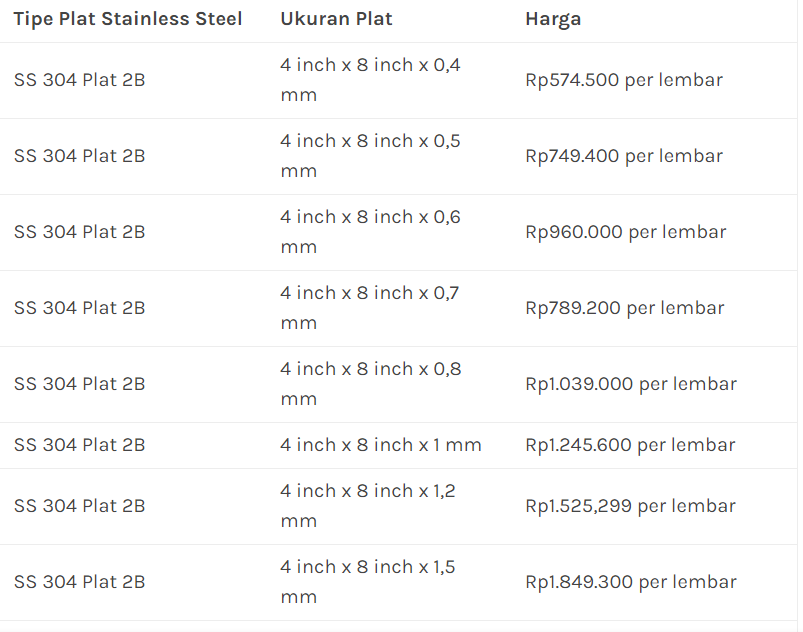
Kemudian dilakukan estimasi pengeluaran berdasarkan data
Hasil yang didapatkan akan berkisar 270.000 rupiah - 300.000 rupiah bergantung pada pembulatan angka ketebalan, jari-jari dan tinggi tabung.