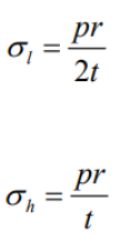Difference between revisions of "Muhamad Sabran Jamil"
(→Final Remarks) |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
== Resume Pertemeuan 26 Mei 2023 == | == Resume Pertemeuan 26 Mei 2023 == | ||
| + | Pada pertemuan awal ini, kami membahas beberapa topik terkait pengenalan dan konsep dasar dalam pembelajaran Metode Numerik. | ||
| + | |||
| + | Pak Ahmad Indra Siswantara (DAI) memberikan penjelasan mengenai minat mahasiswa terhadap mata kuliah Metode Numerik. Beliau menekankan pentingnya bagi kita sebagai mahasiswa untuk memanfaatkan potensi diri selama masih muda dan berusaha semaksimal mungkin dalam memahami materi yang sedang dipelajari selama perkuliahan. | ||
| + | |||
| + | Di era saat ini, ada teknologi bernama Chat GPT yang dapat kita manfaatkan sepenuhnya untuk mendapatkan data dan mencari informasi konkret mengenai materi yang membingungkan kita. | ||
| + | |||
| + | Pak DAI juga menjelaskan tentang metode ujian yang akan digunakan dalam kelas ini. Metode "Blank Paper Question Sheet" akan diterapkan, di mana mahasiswa diberi kesempatan untuk menulis dan membuat materi serta pertanyaan berdasarkan ilmu yang telah mereka peroleh selama mengikuti perkuliahan. Pak DAI berharap agar mahasiswa memahami materi yang telah disampaikan dan menggambarkannya dalam lembaran kertas yang diberikan. | ||
| + | |||
| + | Pada pertemuan pertama ini, Pak DAI juga meminta beberapa mahasiswa untuk menjelaskan apa yang mereka pelajari selama mengikuti kelas Metode Numerik. | ||
| + | |||
| + | Selanjutnya, Pak DAI mengingatkan tentang materi yang dikirimkan melalui Grup WhatsApp dan memberikan penjelasan singkat mengenai tugas kepada mahasiswa untuk membuat dan mengoptimalkan tabung hidrogen dengan batasan biaya produksi kurang dari Rp500.000. Tugas ini diberikan dengan pertimbangan bahwa di masa depan, energi hidrogen diharapkan menjadi solusi energi yang tidak mencemari lingkungan dan tidak menghasilkan limbah akibat pertukaran energi. | ||
| + | |||
| + | Pada akhir sesi perkuliahan, Pak DAI memberikan studi kasus dan analogi pendekatan yang menginspirasi mahasiswa untuk lebih tekun dalam menimba ilmu dan mendekatkan diri kepada Tuhan Yang Maha Esa, agar selama perjalanan perkuliahan kita selalu ingat bahwa tidak ada yang sempurna dan pasti kecuali-Nya. | ||
| + | |||
| + | == '''My concious efforts in numerical method learning and its application in hydrogen storage design optimization''' == | ||
| + | [https://www.youtube.com/watch?v=4UhFqmhgyZ8] | ||
| + | <youtube width="400" height="200">v=4UhFqmhgyZ8</youtube> | ||
Latest revision as of 03:19, 16 June 2023
Intoduction Saya Muhamad Sabran Jamil dari provinsi Riau dan lahir pada 17 Meni 2003. Pada saat ini berkuliah di Universitas Indonesia
Contents
- 1 Resume Pertemeuan 26 Mei 2023
- 2 My concious efforts in numerical method learning and its application in hydrogen storage design optimization
- 3 Report of Design & Optimization of Pressurized Hydrogen Storage (First Progression)
- 4 Final Report of Design & Optimization of Pressurized Hydrogen Storage
- 5 Batasan Geometris (Geometrical Constraint)
- 6 Geometri Dasar (Base)
- 7 Geometri End Cap
- 8 Batasan Kekuatan Material (Material Strength Constraint)
- 9 Mechanical Properties of AISI 304 Austenitic Stainless Steel
- 10 Batasan Biaya (Budget Constraint)
- 11 Final Remarks
Resume Pertemeuan 26 Mei 2023
Pada pertemuan awal ini, kami membahas beberapa topik terkait pengenalan dan konsep dasar dalam pembelajaran Metode Numerik.
Pak Ahmad Indra Siswantara (DAI) memberikan penjelasan mengenai minat mahasiswa terhadap mata kuliah Metode Numerik. Beliau menekankan pentingnya bagi kita sebagai mahasiswa untuk memanfaatkan potensi diri selama masih muda dan berusaha semaksimal mungkin dalam memahami materi yang sedang dipelajari selama perkuliahan.
Di era saat ini, ada teknologi bernama Chat GPT yang dapat kita manfaatkan sepenuhnya untuk mendapatkan data dan mencari informasi konkret mengenai materi yang membingungkan kita.
Pak DAI juga menjelaskan tentang metode ujian yang akan digunakan dalam kelas ini. Metode "Blank Paper Question Sheet" akan diterapkan, di mana mahasiswa diberi kesempatan untuk menulis dan membuat materi serta pertanyaan berdasarkan ilmu yang telah mereka peroleh selama mengikuti perkuliahan. Pak DAI berharap agar mahasiswa memahami materi yang telah disampaikan dan menggambarkannya dalam lembaran kertas yang diberikan.
Pada pertemuan pertama ini, Pak DAI juga meminta beberapa mahasiswa untuk menjelaskan apa yang mereka pelajari selama mengikuti kelas Metode Numerik.
Selanjutnya, Pak DAI mengingatkan tentang materi yang dikirimkan melalui Grup WhatsApp dan memberikan penjelasan singkat mengenai tugas kepada mahasiswa untuk membuat dan mengoptimalkan tabung hidrogen dengan batasan biaya produksi kurang dari Rp500.000. Tugas ini diberikan dengan pertimbangan bahwa di masa depan, energi hidrogen diharapkan menjadi solusi energi yang tidak mencemari lingkungan dan tidak menghasilkan limbah akibat pertukaran energi.
Pada akhir sesi perkuliahan, Pak DAI memberikan studi kasus dan analogi pendekatan yang menginspirasi mahasiswa untuk lebih tekun dalam menimba ilmu dan mendekatkan diri kepada Tuhan Yang Maha Esa, agar selama perjalanan perkuliahan kita selalu ingat bahwa tidak ada yang sempurna dan pasti kecuali-Nya.
My concious efforts in numerical method learning and its application in hydrogen storage design optimization
Report of Design & Optimization of Pressurized Hydrogen Storage (First Progression)
Sebagai mahasiswa Teknik Perkapalan yang sedang menjalani pendidikan untuk menjadi insinyur yang berkualitas, penting bagi kita untuk mengambil pendekatan menyeluruh dalam mendesain komponen-komponen, terutama dalam hal efisiensi dan optimisasi. Salah satu tugas dalam kelas Metode Numerik adalah merancang dan mengoptimalkan penyimpanan hidrogen bertekanan tinggi, yang memberi kita kesempatan untuk mengembangkan pola pikir insinyur. Selain itu, hal ini juga membantu meningkatkan kesadaran kita terhadap berbagai aspek terkait.
Parameter:
1. Harga di bawah Rp500.000,00
2. Tekanan = 8 bar
3. Volume = 1 liter
Certainly! Designing and optimizing a cost-effective compact pressurized hydrogen storage system involves considering several essential elements and following specific procedures:
Determine System Requirements: Identify the specific needs for the hydrogen storage system, such as storage capacity, operating pressure, weight, dimensions, and safety considerations. These requirements will serve as guidelines for the design process.
Select Storage Method: Choose the appropriate storage method based on the application and requirements. In this case, the focus is on pressurized hydrogen storage. Other methods include cryogenic storage, solid-state storage, and chemical storage.
Choose Suitable Materials: Select materials that are safe, cost-effective, and efficient. The storage vessel should be strong, compatible with hydrogen, and have low permeability to prevent leaks. Common materials include high-strength steel, carbon fiber composites, or polymer-based liners with carbon fiber wrapping.
Design the System: Develop a detailed design for the storage system, considering factors such as vessel shape, volume, structural integrity, valve and fitting placement, thermal management, and pressure relief mechanisms. Computer-aided design (CAD) software can assist in creating accurate models.
Implement Safety Measures: Incorporate safety features to ensure reliable operation and prevent accidents. This may include pressure relief devices, burst disks, pressure sensors, and fire suppression systems. Adhering to relevant safety standards, such as ISO 16111 or ASME Boiler and Pressure Vessel Code, is essential.
Optimize for Cost-effectiveness and Compactness: Use optimization techniques such as structural analysis, computational fluid dynamics (CFD) simulations, and optimization algorithms to refine the design for cost-effectiveness and compactness. These methods help identify the most efficient shapes, materials, and manufacturing techniques to reduce costs and maximize storage capacity.
Choose Manufacturing Process: Select a manufacturing process that balances cost, quality, and scalability. Common methods for hydrogen storage vessels include filament winding for composite materials and deep-drawing or forging for metal containers. Continuously improve the manufacturing process to reduce costs and enhance reliability.
Perform Performance Testing: Conduct comprehensive performance tests to ensure the system meets the desired specifications and safety requirements. This may involve pressure cycling, leak testing, burst tests, and other relevant evaluations. Simulate real-world conditions as accurately as possible.
Ensure Regulatory Compliance: Comply with relevant regulations and standards for hydrogen storage systems. This may include obtaining certifications from regulatory bodies such as ISO, the U.S. Department of Transportation (DOT), or local regulatory agencies. Compliance is crucial for market acceptance and safety.
Consider Lifecycle Implications: Evaluate the lifecycle impact of the storage system, considering factors such as material sourcing, manufacturing energy consumption, maintenance requirements, and end-of-life considerations. Aim for sustainability and minimize environmental impact.
Continuously Improve: Stay updated on advancements in hydrogen storage systems, including new technologies and materials. Continually seek opportunities to enhance system efficiency, reduce costs, and improve safety through ongoing research and development efforts.
Final Report of Design & Optimization of Pressurized Hydrogen Storage
Dalam merancang tangki hidrogen ini, terdapat tiga batasan yang harus diperhatikan, yaitu batasan geometris, kekuatan material, dan biaya. Setelah melakukan diskusi dengan teman-teman dalam kelas, kami memutuskan untuk menggunakan baja tahan karat austenitik AISI 304 sebagai material untuk tangki hidrogen ini. Pilihan ini sejalan dengan praktek yang umum dilakukan oleh pabrikan-pabrikan penyimpanan hidrogen industri. Austenitic stainless steel telah terbukti memiliki ketersediaan yang baik, daya tahan yang tinggi, kekuatan yang memadai, kemudahan dalam proses pembuatan, kompatibilitas dengan gas hidrogen (tidak bereaksi dengan hidrogen), dan sebagainya.
Batasan Geometris (Geometrical Constraint)
Geometri Dasar (Base)
Salah satu komponen utama dalam mendesain penyimpanan hidrogen bertekanan adalah pengukuran dan geometri dari penyimpanan tersebut. Melalui diskusi di kelas dan studi kasus individu, mahasiswa di kelas kami sepakat bahwa bentuk ideal dari penyimpanan tersebut adalah berbentuk silinder seperti yang umumnya digunakan dalam industri. Namun, parameter dari bentuk silinder tersebut masih perlu ditentukan menggunakan metode-metode Numerik.
Tujuan dari proses optimisasi penyimpanan hidrogen ini, seperti yang disebutkan dalam studi kasus sebelumnya, adalah menciptakan penyimpanan hidrogen bertekanan yang memenuhi persyaratan sambil tetap efisien biaya. Salah satu faktor utama yang memengaruhi biaya produksi adalah jumlah bahan yang digunakan, yang dalam kasus wadah silinder, sebanding dengan luas permukaan produk. Semakin kecil luas permukaan total, semakin sedikit bahan yang dibutuhkan untuk membuatnya. Pada kasus kita, luas permukaan perlu diminimalkan sambil mempertahankan volume sebesar 1 liter atau 1000 sentimeter kubik. Jari-jari dan tinggi dari silinder yang memenuhi kedua kriteria tersebut dapat ditentukan menggunakan fungsi optimisasi sederhana yang dapat dihitung secara numerik menggunakan kode yang sesuai dibuat dengan Python atau MATLAB, dan berbagai perangkat lainnya, seperti C+, C++, dll. Dalam merancang Projek ini, saya menggunakan Python untuk membuat kode yang secara manual menghitung jari-jari dan tinggi dari sebuah silinder dengan volume 1000 sentimeter kubik. Meskipun ada pustaka seperti SciPy yang telah menyediakan fungsi optimisasi yang telah dikompilasi sebelumnya, tetapi dalam rangka mempelajari konsep yang mendasarinya, saya memilih untuk mengimplementasikan kode secara manual. Berikut adalah hasil kodingan saya:
import math
from scipy.optimize import minimize
def calculate_surface_area(x):
radius, height = x
surface_area = 2 * math.pi * radius * (radius + height)
return surface_area
def calculate_optimized_dimensions(volume):
volume_cm3 = volume * 1000
objective = lambda x: calculate_surface_area(x)
constraint = lambda x: volume_cm3 - (math.pi * x[0]**2 * x[1])
x0 = [1, 1]
bounds = ((0, None), (0, None))
volume_constraint = {'type': 'eq', 'fun': constraint}
result = minimize(objective, x0, method='SLSQP', bounds=bounds, constraints=volume_constraint)
optimized_radius = result.x[0]
optimized_height = result.x[1]
optimized_surface_area = result.fun
return optimized_radius, optimized_height, optimized_surface_area
volume = 1
radius, height, surface_area = calculate_optimized_dimensions(volume)
print("Optimized Dimensions:")
print(f"Radius: {radius} cm")
print(f"Height: {height} cm")
print(f"Surface Area: {surface_area} cm^2")Optimized Dimensions:
Radius: 5.41926305506462 cm
Height: 10.838511985088449 cm
Surface Area: 553.5810444905989 cm^2Geometri End Cap
Menggunakan geometri yang sepenuhnya berbentuk silinder untuk tangki penyimpanan kemungkinan akan berbahaya karena adanya sudut di ujung-ujungnya, yang dapat menyebabkan konsentrasi tegangan atau titik kegagalan. Sebagian besar bejana bertekanan menggunakan bentuk melengkung pada ujungnya untuk mengurangi konsentrasi tegangan dengan menggunakan tiga geometri: setengah bola (hemispherical), elipsoida (ellipsoidal), dan torispherical. Urutan penambahan volume dan luas permukaan tertinggi ke yang terendah juga mengikuti urutan yang sama. Oleh karena itu, karena tujuan kita adalah untuk meminimalkan luas permukaan sambil mempertahankan volume yang sama, paling efisien untuk menggunakan penutup ujung berbentuk torispherical. Bentuk torispherical dapat disederhanakan sebagai bentuk silinder yang diberi filleting parsial. Penyesuaian filleting ini akan mengurangi volume keseluruhan struktur. Oleh karena itu, kita perlu menyesuaikan parameter geometri untuk mengompensasi pengurangan akibat filleting untuk menciptakan penutup ujung.
Kita dapat menetapkan fillet dengan radius setengah dari jari-jari wadah untuk menciptakan kelengkungan yang halus guna mengurangi konsentrasi tegangan yang lebih besar. Telah dibuat contoh sketsa melalui program desain berbantu komputer untuk memvisualisasikan pengurangan luas penampang dari sisi lingkarannya. Berdasarkan hukum proporsionalitas, pengurangan persentase dalam luas penampang akan sama dengan pengurangan persentase dalam volume yang sama. Oleh karena itu, kita dapat menghitung pengurangan persentase dan menerapkannya secara terbalik pada volume yang kita butuhkan untuk mendapatkan batasan volume yang baru.
Seperti yang ditunjukkan, dengan asumsi radius fillet setengah dari jari-jari wadah, kita memiliki batasan volume baru sebesar 1060 sentimeter kubik untuk memperhitungkan pengurangan persentase volume setelah pembentukan penutup ujung torispherical melalui filleting. Kita dapat mengulangi proses iterasi yang sebelumnya digunakan untuk mendapatkan nilai-nilai jari-jari dan tinggi baru untuk silinder. Setelah mengulangi bagian pertama kode, kita menemukan bahwa luas permukaan minimum terjadi antara nilai jari-jari 5 dan 6 cm lagi, sehingga batas atas dan bawah dari set kode kedua tidak perlu disesuaikan. Hasil akhirnya adalah sebagai berikut:
R = 5.42
H = 10.84
x = 1000
r = 2.78
def equation(y):
return ((R * H - 2 * ((r**2) - 3.14 * (r**2) / 4)) / (R * H)) - (x / y)
def solve_equation():
y = 1
while True:
f = equation(y)
df = (equation(y + 1e-6) - f) / 1e-6
y -= f / df
if abs(f) < 1e-6:
break
return y
y_value = solve_equation()
print("The value of y is approximately:", y_value)
Dengan Hasil akhir sebagai berikut:
The value of y is approximately: 1059.9537561057862
y=Volume yang diinginkan=1060 cm^3 (dibulatkan)import math
volume = 1060 # ml
min_radius = 5
max_radius = 6
step = 0.01
surface_list = []
radius = min_radius
while radius <= max_radius:
cylinder_surface = 2 * (math.pi * radius**2) + (2 * math.pi * radius * volume / (math.pi * radius**2))
surface_list.append((cylinder_surface, radius))
radius += step
minimum_surface, optimized_radius = min(surface_list)
print('Minimum surface area and radius: ', minimum_surface, optimized_radius)
optimized_height = volume / (math.pi * optimized_radius**2)
print("Optimized Dimensions:")
print("Radius of 1056.69 ml tank: {:.2f} centimeters".format(optimized_radius))
print("Height of 1056.69 ml tank: {:.2f} centimeters".format(optimized_height))
print("Ratio of height to radius of a minimized surface: {:.2f}".format(optimized_height / optimized_radius))Minimum surface area and radius: 575.5089335313951 5.529999999999989
Optimized Dimensions:
Radius of 1056.69 ml tank: 5.53 centimeters
Height of 1056.69 ml tank: 11.03 centimeters
Ratio of height to radius of a minimized surface: 2.00Batasan Kekuatan Material (Material Strength Constraint)
Dalam konteks wadah bertekanan, memastikan ketebalan dan kekuatan bahan wadah dapat menahan tekanan yang diberikan pada dindingnya sangat penting. Dalam komponen silinder tipis, ada dua jenis tegangan utama: tegangan sirkumferensial (hoop) dan tegangan longitudinal. Meskipun tegangan radial ada, itu dapat diabaikan karena radiusnya jauh lebih besar dari ketebalan dinding. Rumus yang diberikan di bawah ini dapat digunakan untuk menghitung tegangan hoop dan tegangan longitudinal:
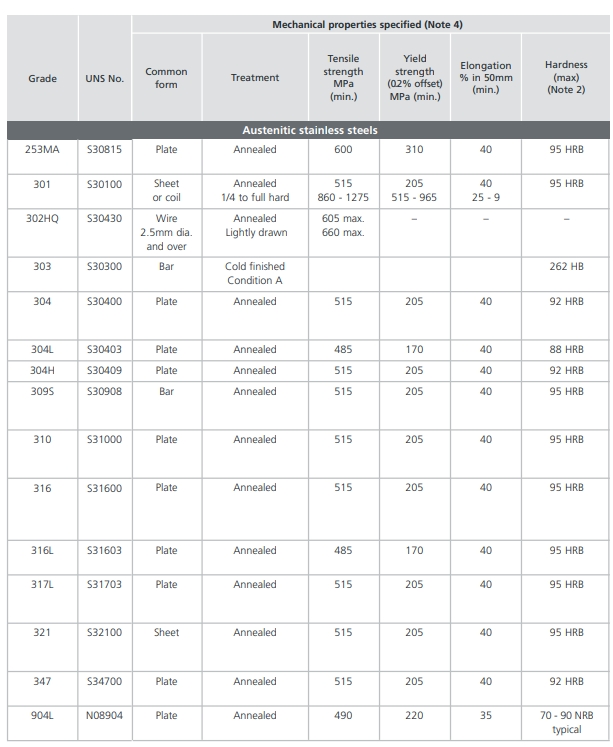
Mechanical Properties of AISI 304 Austenitic Stainless Steel
Berdasarkan ASME BPV Code Section VIII D.1, ketebalan minimum pelat tangki harus setidaknya 1/16 in atau 1,59 mm tanpa mempertimbangkan faktor korosi, material, atau dimensi. Dalam perhitungan ini, akan dilakukan serangkaian iterasi dimulai dari radius minimum 2,8 mm hingga 12 mm dengan penambahan 1 mm setiap iterasi.
r = 5.53e-2
p = 800000
t = 2.8e-3
while t < 12e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 0.1e-3
if hoop > 205e9:
breakBatasan Biaya (Budget Constraint)
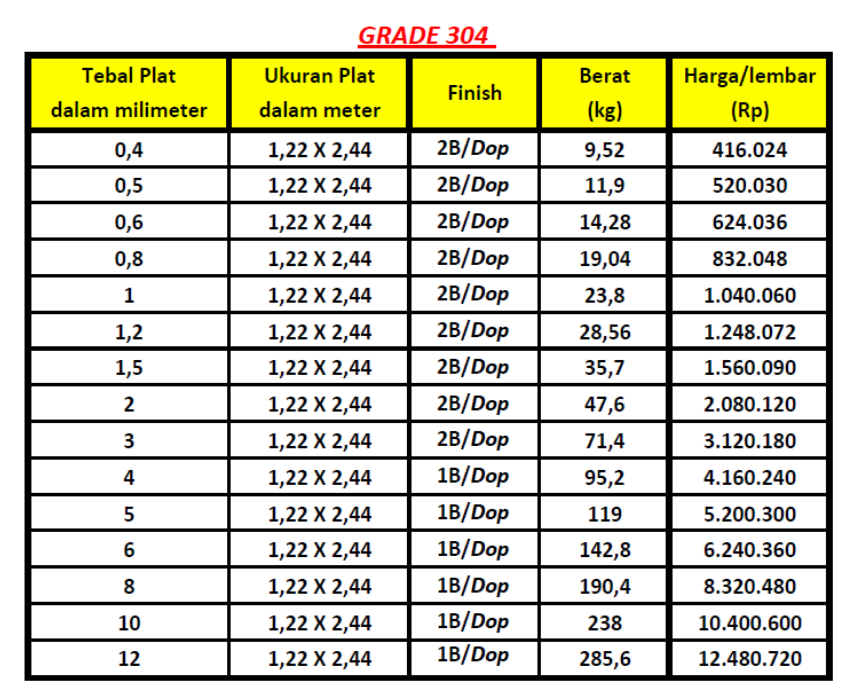
Setelah mendapatkan parameter-parameter geometris yang relevan, langkah terakhir dalam proses optimisasi ini adalah membandingkannya dengan batas biaya yang telah ditetapkan sebesar Rp500.000,00. Dengan mempertimbangkan material yang telah dipilih sebelumnya, yaitu AISI 304, kita perlu memilih ketebalan dinding tangki yang sesuai dengan kisaran anggaran yang telah ditentukan. Berikut adalah daftar harga beserta perhitungannya.
Link Harga: https://ptcitraanggunlestaridotcom.wordpress.com/
Tabel di atas menyajikan rentang ketebalan yang sudah disempitkan dalam area yang menjadi fokus kita. Dengan melakukan analisis biaya per luasan berdasarkan data dari PT Citra Anggun Lestari didapatkan semua nilai ketebalan yang mungkin memenuhi batasan biaya. Dalam pemilihan ketebalan, saya juga mempertimbangkan untuk meminimalkan berat sambil mempertahankan kekuatan yang cukup dengan pilihan optimal adalah ketebalan dinding 8 mm.
Final Remarks
Berdasarkan penerapan metode numerik dalam optimisasi desain sistem penyimpanan hidrogen ini, ditemukan dimensi geometris tangki yang optimal, yaitu radius sebesar 5,53 cm, tinggi sebesar 11,03 cm, luas permukaan sebesar 575,51 cm, dan radius fillet end cap sebesar 2,78 cm. Dalam melakukan optimisasi, juga mempertimbangkan batasan kekuatan material dan batasan biaya, sehingga diperoleh ketebalan dinding tangki hidrogen sebesar 8 mm.
Secara keseluruhan, metode numerik dalam optimisasi ini masih tergolong sederhana karena terdapat banyak faktor lain yang perlu dipertimbangkan. Namun, optimisasi sederhana ini dapat memberikan latihan bagi kita sebagai mahasiswa Teknik Perkapalan dalam berpikir secara insinyur yang mampu memanfaatkan dan memaksimalkan sumber daya yang ada. Melalui tugas besar ini, diharapkan kesadaran kita juga semakin terlatih dan meningkat.